基于EGARCH-εt-GPD模型的VaR计算
2015-03-03冯长焕何沁洋
唐 宁,冯长焕,何沁洋
(西华师范大学 数学与信息学院,四川 南充 637002)
基于EGARCH-εt-GPD模型的VaR计算
唐 宁,冯长焕,何沁洋
(西华师范大学 数学与信息学院,四川 南充 637002)
在传统的利用极值理论来计算VaR的过程中,一般先是对时间序列建立GARCH模型,再对残差序列运用极值理论建模,从而估计得到VaR.但建模时在GARCH模型的条件方差方程中,人们只考虑了以前时刻的随机误差项对方差的影响,而忽视了当前时刻的随机误差项对方差所作出的贡献.故作者在对时间序列建立EGARCH模型时,在方差方程中引进了当前时刻的随机误差项,然后再对残差建立GPD模型来研究风险价值,并进行了相应的实证分析,结果表明加入当前时刻的随机误差项后估计得到的VaR准确性更高.
EGARCH模型; GPD分布; 极值理论; VaR
1 预备知识
近年来,由于种种原因金融时间序列的波动性日益增大,正是因为这种波动所具有的不确定性导致了人们极其关注金融市场可能存在的风险价值(VaR),所以衍生出了许多计算VaR的方法.
在利用传统方法计算VaR时常常假设收益率序列服从正态分布.但是随着人们进一步的研究发现金融时间序列存在波动集聚性、尖峰厚尾性和杠杆效应,故一般的正态分布假设已不再满足要求,于是许多学者又假设序列服从稍满足尖峰厚尾的t分布或GED分布等,但是并非所有的金融数据都完全服从t分布或GED分布,且VaR主要是对极值的估计,故人们又将极值理论应用到了VaR的计算中.对于利用极值理论计算VaR的研究已经有许多,如:2003年张国辉在论文《极值理论及其在风险价值中的应用》[1]中利用极值理论讨论了具有厚尾特性的上证指数的VaR值;2008年欧阳资生基于指数回归模型构造了厚尾分布的极值分位数估计,得到了VaR的计算公式[2];因很多金融时间序列不满足极值理论所要求的相互独立这一条件,所以2013年俞慧琴将GARCH模型与GPD模型结合形成了GARCH-GPD模型,利用极值理论分析了具有高峰厚尾和波动集聚性的收益率的VaR,并进行了相应的实证分析,说明了基于GARCH-GPD模型下的VaR具有一定的优越性[3]等等.
由于EGARCH模型克服了许多GARCH模型的不足且能很好地反应金融时间序列的波动集聚性和杠杆效应,而极值理论中GPD模型能很好地刻画尾部极值的分布,故本文在加入了当前时刻的随机误差项后,将EGARCH模型和GPD模型结合,利用EGARCH-εt-GPD模型研究了风险价值.
2 理论知识
2.1 EGARCH模型
为了在反映方差时变性的同时刻画金融时间序列的杠杆效应,学者将Engle定义的ARCH(q)模型:
(1)
(2)
中的均值方程(1)保持不变,而将条件方差方程(2)改为:
(3)
形成了EGARCH(p,q)模型.然而从EGARCH模型的条件方差方程(3)可看出,在计算t时刻的方差时,人们只考虑了t时刻以前的随机误差项对方差的影响,而忽视了当前时刻的随机误差项对方差所作出的贡献,为了弥补这一不足,故本文在方差方程中引进当前时刻的随机误差项并结合金融时间序列的实际情况建立了加入当前随机误差项的EGARCH-εt模型:
其中εt是由计算机随机产生的当前时刻的随机误差项,其值满足均值与方差等于t时刻以前的误差项的均值与方差.
2.2 VaR定义
VaR被定义为:在一给定的置信水平下,预计资产在将来某一时间段内可能的最大损失.即:
(4)
其中Rt为资产在第t期的收益率,VaRt为t时刻α水平下的VaR(从VaR的定义可知VaR的本质是概率分布函数的分位数).
将(4)式作适当的变形可得EGARCH模型下收益率序列的VaREGARCH与经EGARCH模型过滤后得到的残差序列εt的VaRε之间的关系;
(5)
其中ut和σt分别是t时刻序列的均值和标准差.由于计算得到的ut非常小,故可用总体均值代替
2.3 极值理论——广义帕累托分布(GPD)

(6)
当u充分大时Fu(y)≈Gτ,σ(y)(GPD分布),其中
(7)
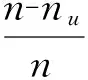
(8)
从而由尾部估计公式求分位数函数得到VaR为:
(9)
其中公式(9)中的参数σ,τ是对GPD采用极大似然法估计得到的.
在利用极值理论计算VaR时一般要求序列是独立同分布的,但通常情况下收益率序列本身却存在着自相关性,然而在经EGARCH模型过滤后得到的残差序列εt可满足独立同分布这一条件,故可通过以下思想来计算收益率序列的VaR:首先对收益率序列用时间序列模型拟合,得到残差序列,再判断残差序列是否近似为独立同分布序列,若满足,则用GPD模型拟合残差序列并估计残差VaR,最后再根据(5)式由残差序列的VaR计算得到收益率序列的VaR.
3 实证分析
3.1 数据来源及处理分析
本文采用上证指数2009-01-01到2014-07-31的日收盘价为样本,共1 351个数据进行实证分析,数据来源于网易财经网.本文对收盘价的处理为Rt=-(lnPt-lnPt-1)(Pt为资产在t时刻的价格),经处理后共1 350个数据.利用eviews6.0对序列Rt进行分析得到如下结果:
1)对序列Rt作单位根ADF检验,其t统计量的值为-36.125 09小于-3.434 987,即在0.01的显著水平下序列Rt平稳.
2)序列Rt的偏度为0.375 715大于0,峰度为 5.375 576大于3,说明序列Rt具有高峰厚尾性,且JB统计量的伴随概率为0.000小于0.05,所以序列Rt不服从正态分布.
3)对Rt进行ARCH效应的LM检验,其结果表明2阶以后的LM统计量的伴随概率均小于0.05,说明残差具有高阶的ARCH效应,且金融时间序列常存在杠杆效应,所以对收益率序列Rt建立EGARCH比较合理.
3.2 建立模型并进行参数估计
3.2.1 对序列Rt建立ARMA-EGARCH-εt模型
尽管EGARCH(p,q)模型能很好地刻画金融时间序列的异方差性和杠杆效应,但为了进一步准确地刻画收益率序列的VaR,本文在多次尝试后利用在方差方程中加入当前时刻随机误差项的EGARCH(1,1)-εt模型对处理后的上证指数日收益率序列Rt进行拟合,相关参数估计结果如表一.

表1 Rt序列EGARCH(1,1)-εt模型的参数估计结果
故加入当前时刻残差后的条件方差方程为:
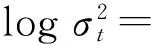
而传统EGARCH(1,1)模型的相关参数估计结果为:

表2 Rt序列EGARCH(1,1)模型的传统参数估计结果
故传统的条件方差方程为:
3.2.2 对残差序列建立GPD模型
经检验,对序列Rt建立ARMA-EGARCH-εt模型后的残差序列εt是独立且不服从正态分布的近似白噪声序列,故可对残差εt建立GPD模型.而建立GPD模型的关键是确定阀值,阀值过大或阀值过小都直接影响到模型准确性,结合所采用的数据特点,本文选取数据1.655 454 777作为阀值来估计GPD模型中的参数.利用极大似然法估计出参数σ=3.850 8,τ=-0.718 1,从而由公式(9)可估计出残差VaRε=1.571 106 34.
3.3 计算收益率VaR并进行后验检验
结合ARMA-EGARCH-εt模型的估计结果、估计出的残差VaRε和公式(5)可得不同置信水平下加入当前随机误差项的EGARCH-εt-GPD模型的VaR值.
本文计算了置信度为95%的后300天的VaR,部分计算结果如表3.

表3 EGARCH-εt-GPD模型下的部分VaR值
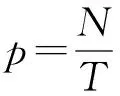
在估计出的300天中损失超过VaR的天数为15天,失败率为0.05.故通过EGARCH-εt-GPD模型计算得到的VaR是准确的.
4 结论
本文首先通过在方差方程中加入当前随机误差项对上证指数的收益率序列建立ARMA-EGARCH-εt模型进行拟合,拟合的方差方程为:
这样既刻画了收益率序列的尖峰厚尾性和杠杆效应,也消除了ARCH效应,然后再对残差序列应用极值理论建立了GPD模型,最后根据收益率序列的VaREGARCH与残差序列εt的VaR的关系计算了后300天的EGARCH-εt-GPD模型VaR值(表3),经后验检验其失败率为0.05,说明得到的VaR准确性较高.而由传统EGARCH-GPD模型计算出的VaR值(表4),其失败率为0.043,这说明加入当前随机误差项的VaR值更准确.

表4 传统EGARCH-GPD模型下的部分VaR值
由加入当前时刻的随机误差项得到的EGARCH-εt-GPD模型的VaR,其最大值为0.261 071 54,最小值为0.011 870 679,均值为0.017 276 371.而由传统的EGARCH-GPD模型的VaR,其最大值为0.24 305 007,最小值为0.011 862 958,均值为0.017 023 241.这说明从总体上来说,加入当前时刻的随机误差项后所计算得出的VaR比直接计算得到的VaR稍大,故此种方法适用于对风险价值比较敏感的金融行业.
[1] 张国辉.极值理论及其在风险价值中的应用[D].杭州:浙江大学,2003
[2] 欧阳资生.厚尾分布的极值分位数估计与极值风险测度研究[J].数理统计与管理,2008(1):70-75
[3] 俞慧琴.基于极值理论VaR模型的上市公司行业风险比较研究[D].杭州:浙江大学,2013
The Calculation of VaR Based on EGARCH-εt-GPD Model
Tang Ning, Feng Changhuan,He Qinyang
(School of Mathematics and Information,China West Normal University, Nanchong 637002,China)
In the process of calculating the VaR by the traditional extremum theory, generally in the first the GARCH model is set up on the time sequence, and then, the extremum theory is adopted to model the residual sequence so as to estimate the VaR. But when modeling in the conditional variance equation of the GARCH model, people only consider the influence of the random error term of the past on the variance while ignoring the contribution made by the random error term of the current to the variance. Therefore, when the EGARCH model is set up on the time series by the author, the random error term of the current is brought in the variance equation. And, the GPD model is built on the residual error to study its value at risk and to analyze it empirically. The result shows that the accuracy of the VaR is higher by the way that the VaR is incorporated with the random error term of the current.
EGARCH model; GPD distribution; extreme value theory; VaR
2014-12-26 基金项目:西华师范大学基本科研业务费专项资金资助(14C004);南充市社科规划一般规划课题(NC2013B027).
唐 宁(1991-), 女,西华师范大学数学与信息学院硕士研究生,主要从事统计学理论及应用研究.
1672-2027(2015)01-0054-04
TP311
A
