青藏铁路含保温夹层路基厚度与地温关系的研究
2015-03-03刘彩云郭尊光
刘彩云,郭尊光
(太原工业学院 理学系,山西 太原 030008)
青藏铁路含保温夹层路基厚度与地温关系的研究
刘彩云,郭尊光
(太原工业学院 理学系,山西 太原 030008)
通过对青藏铁路风火山段含有保温夹层的路基建立均匀介质分层纯导热模型并运用分层近似解法求出冻土表层的温度函数,结合Lachenbruch给出的冻土层的理论温度表达式,得到了路基填料层、保温层、地表年平均温度与正弦变化温度的振幅比三者之间的隐式方程,并应用该方程对三者之间的关系进行了分析.
多年冻土;保温层;分层纯导热模型;分层近似解
0 引言

20世纪60年代,美国冻土专家Lachenbruch指出在冻土区如果地表有一个正弦变化的温度场T=B+Asinωt,那么在较长时间内,地下任意深度处的温度也是按正弦变化,其频率与地表温度的频率相同,但振幅会随着深度的增加而逐渐衰减.因此,在地下任意深度处的理论温度为:T=B+A′sinωt[2].20世纪70年代起, 前苏联、日本、美国、加拿大等国家开始采用聚苯乙烯(EPS)作为路基保温材料, 取得了良好的效果.20世纪70年代中期, 我国开始对铺设EPS保温材料的路基稳定性进行研究并对其效果作了充分的肯定[3].随后,我国冻土界专家、工程设计师通过采集工程现场数据,采用数值模拟对青藏高原多个冻土区路基临界高度、路基地基处理、路基地温预测及含保温夹层的路基温度场进行研究[4,5,6].本文通过对青藏铁路风火山段含有保温夹层的路基建立三层分层纯导热模型,运用分层近似解法求出冻土层的温度函数,结合Lachenbruch给出的冻土层的理论温度表达式,得到了路基填料层、保温层、地表年平均温度与正弦变化温度的振幅比三者之间的隐式方程,通过该隐式方程对三者之间的关系进行了分析.
1 模型的建立
1)假设路基由三部分构成:碎石、EPS保温层、多年冻土.路基的示意图如图1,路基中材料的热物性参数如表1.
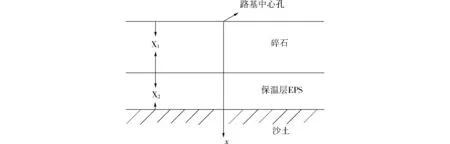
图1 青海-西藏铁路风火山段路基中心孔的示意图

表1 碎石、冻土层土壤及保温层的热物性参数
2)风火山段地表年平均气温为-4.5 ℃到-0.5 ℃,土体融化与冻结变化很小,因此可忽略冰-水的相变.
3)本文主要研究铺设路基后地表温度对冻土层的影响,故取路基中心孔的垂直正下方作为研究对象.由于碎石与保温板含水量极少,青藏高原土体含水量不高,因此可忽略对流、质量迁移、水热蒸发和其它作用.
基于以上三点假设,可将路基温度场视为半无界区域内三层均匀介质的分层纯导热问题,模型如下:
(1)
(2)
(3)
T1(0,t)=B+Asinωt,x=0
(4)
T1(x,0)=T2(x,0)=T3(x,0)=0,x>0
(5)
T1(X1,t)=T2(X1,t),x=X1
(6)
(7)
T2(X1+X2,t)=T3(X1+X2,t),x=X1+X2
(8)
(9)
(10)

2 模型求解
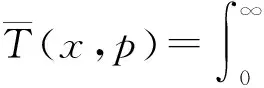
(11)
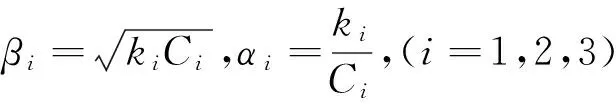
其中j=1,2.
3 结论
上述模型中得到的路基下伏冻土表层温度函数关系式恰好与Lachenbruch的冻土层的理论温度表达式一致,将两者结合可得路基填料层、保温层、地表年平均温度与正弦变化温度的振幅比三者之间的隐式方程:
(12)
假设风火山段土壤中水的冻结温度为0 ℃,要使路基下的永久冻土在使用期限内一直处于稳定的冻结状态,则理论温度振幅A′≤|B|,本文令A′=|B|=1.0
3.1 填料层厚度与保温层厚度之间的变化关系
从图2中可以看出,填料层厚度随着保温层厚度的增加而逐渐减小.如果不铺设保温层,则填料层的厚度需达到7.84 m才可从理论上保证冻土层上限不变,但是这会导致工程造价太高,同时考虑边坡力学的稳定性及EPS保温材料的应压力等因素,筑路时必须控制填土层的自重力,所筑路堤填料层不宜太高.
另外从图2中可以看出,当保温层厚度大约为40 cm以上时,填料层厚度减小的速率加快.从数学角度考虑,保温层厚度适当加厚有利于降低路基高度,节约工程造价,但太厚的保温层受到较大压力时会发生变形,同样导致路基变形,同时,EPS受压变形后,变为弹柔性材料,使路基中的热交换能力变差,反而影响其热阻性能.因此,在寒区修筑道路时,必须寻求最佳的填土厚度,将填料层与保温层两者结合使用,以保证夹有保温材料的路基在使用期限内稳定.
3.2 地表年平均气温A′与振幅A对保温层厚度的影响
本文取填料层厚度分别为1.5 m,2.0 m与3.0 m三种情况来讨论路基表面的年平均气温与振幅比对保温层厚度的影响.
从图3可以得出,在保证路基热稳定的前提下,随着A′/A的增大,所需保温层厚度迅速减小,保温层厚度对A′/A的比值非常敏感.
假如考虑气候变暖,路基表面的温度为T=-1.0+Gt+12.5sin(2π/8 760)t时(G为气候变暖的速率),路基表面年平均温度的绝对值A′=|-1.0+Gt|随着时间的推移逐渐增小,因此A′/A的比值逐渐减小,在这种情况下随着使用时间的推移,原来路基中铺设的保温层就不足以保证冻土路基在使用期限内一直处于稳定的冻结状态.因此,在寒区修筑道路时,考虑气候变暖的因素极为必要,且在筑路时填料层厚度的适当超估对冻土路基的热稳定性极为有利.

图2 振幅与年平均地表气温不变时填料层与所需保温层厚度之间的变化关系

图3 保温层厚度随A′/A的变化曲线
[1] Ling Feng,Zhang Tingjun.Critical Embankment Height in Fenghuoshan Mountainous Area along the Qinghai-Tibet Railway[J].ISTP Proceedings of 8th International Conference on Permafrost,2003,2:685-689
[2] Lachenbruch.Periodic Heat Flow in a Stratified Medium with Application to Permafrost Problems [M].United States Government Printing Office,1959
[3] 章金钊.工业隔热材料在多年冻土区的应用研究[C].第一届全国寒区环境与工程青年学术会议论文集.兰州:兰州大学出版社,1994
[4] 田亚护,刘建坤.多年冻土区含保温夹层路基温度场的数值模拟[J].中国铁道科学,2002,23(2):59-64
[5] 李 勇,韩龙武.青藏铁路多年冻土路基稳定性及防护措施研究[J].冰川冻土,2011,33(4):880-883
[6] 杨茂林,张 智.浅谈青藏铁路多年冻土区路基处理的技术措施及监理控制要点[J].路基工程,2005(2):71-74
A Study on the Relationship between Roadbed Thickness With Insulation and Earth Temperature of Qinghai-Tibet Railway
Liu Caiyun, Guo Zunguang
(Department of Science,Taiyuan Institute of Technology,Taiyuan 030008,China)
Through the construction of uniform dielectric hierarchy pure heat conduction model of roadbed with insulation in Fenghuo Mountain section of Qinghai-Tibet Railway, combined with the temperature function of permafrost surfaceobtained by hierarchy approximate solution and the theoretical temperature expression of permafrost given by Lunardini, the implicit equation among the packing layer,insulating layer, the annual average surface temperature of roadbed and amplituderelations of sinusoidal variation temperature isobtained. Finally, an analysis of the re-lationship among these three elements is carried out with this equation.
permafrost; insulation; hierarchy pure heat conduc-tion model;hierarchy approximate solution
2014-11-27 基金项目:太原工业学院基金项目(2012LY02).
刘彩云(1982-),女,山西忻州人,硕士,太原工业学院理学系助教,主要从事偏微分方程数值解研究.
1672-2027(2015)01-0066-04
U21
A
