二维平面上的Gauss映射及其性质

王理峰, 石艳玲

(1.南京铁道职业技术学院 社科部,江苏 南京 210031; 2.盐城工学院 基础部, 江苏 盐城 224051)

二维平面上的Gauss映射及其性质

王理峰1, 石艳玲2

(1.南京铁道职业技术学院 社科部,江苏 南京 210031; 2.盐城工学院 基础部, 江苏 盐城 224051)

将一维的Gauss映射及Gauss测度推广至平面上的Gauss映射及Gauss测度,并证明在平面上的Gauss映射与NN×NN上的提升等价,具有保Gauss测度的特点.

连分式;Gauss映射;Gauss测度

1 预备知识

Billingsley[1]给出了一维的Gauss映射及Gauss测度,并研究了相关性质.本文将一维的Gauss映射及Gauss测度推广至平面上的Gauss映射及Gauss测度,并研究平面上的Gauss映射的一些性质.

对于任意实数x∈R都有连分式表达形式如下[1-2]:

其中a0∈Z,当i≥1时ai∈N.

下面先给出R上的一些算子,在本文的讨论中将会经常用到:

定义[1-2]([·]和〈·〉):定义取整函数[·]:R→Z为[·]:x|→z,其中z小于或等于x的最大的整数.x的小数部分由函数〈·〉:R→R给出,定义如下:〈·〉:x|→x-[x].

由于〈x〉=[0;a1,a2,a3,…],我们将考虑x∈(0,1)即a0=0的情形,在下文中[a1,a2,a3,…]即表示[0;a1,a2,a3,…].

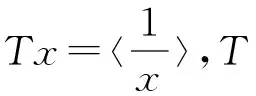
定义[1](Gauss测度):[0,1)上的测度G定义如下:

对任意可测的Ω⊆[0,1].

2 平面上的Gauss映射及Gauss测度的定义

定义:定义映射T:(0,1)×(0,1)→(0,1)×(0,1)为:

称T为二维平面的Gauss映射.

定义:[0,1)×[0,1)上的Gauss测度G定义如下:

对任意可测的Ω⊆[0,1]×[0,1].

易见上面的定义的Gauss测度和 Lebesgue 测度μ具有相同的零测集.所以如果一个命题对于Gauss测度几乎处处成立,那么其对Lebesgue测度几乎处处成立.我们由Gauss测度的定义可以知:

对所有的可测集A⊆[0,1]×[0,1].

3 平面上Gauss映射的一些结论

二维平面的Gauss映射T有如下性质:

定理1:T([a1,a2,a3,…],[b1,b2,b3,…])=([a2,a3,…],[b2,b3,…]),即,Gauss映射

T:(0,1)×(0,1)→(0,1)×(0,1)

与NN×NN上的提升:σ([a1,a2,a3,…],[b1,b2,b3,…])=([a2,a3,…],[b2,b3,…])等价.

证明:

定理2:不可逆影射T:(0,1)×(0,1)→(0,1)×(0,1)是保Gauss测度的.

证明:对任意s>0,t>0,我们验证

GT-1([0,s]×[0,t])=G([0,s]×[0,t])

则定理成立.

易证明:

T-1([0,s]×[0,t])={(x,y):0≤Tx(x,y)≤s,0≤Ty(x,y)≤t}

从而GT-1([0,s]×[0,t])

=G([0,s]×[0,t])

从而定理结论成立.

[1] Billingsley,P.Ergodic Theory and Information[M].New York：Wiley & Sons,1965

[2] Series, C. The modular surface and continued fractions[J].London Math.1985(31):69-80

Gauss Map of the Two-dimensional Plane and Its Properties

Wang Lifeng1, Shi Yanling2

( 1.Dapartment of Social science,Nanjing Railway Vocational and Technical College,Nanjing 210031;

2.Basic Department， Yancheng Institute of Technology, Yancheng 224051, China)

One dimensional Gauss map and Gauss measure are extended to the plane Gauss map and Gauss measure, then show that the Gauss map in the plane corresponds to the shift on and preserves Gauss measure.

continued fraction;Gauss map; Gauss measure

2014-11-21

江苏省普通高校研究生科研创新计划项目(CXZZ12-0083);江苏省高校哲学社会科学研究基金项目(2014SJD283).

王理峰(1981-),女,河南平顶山人,硕士,南京铁道职业技术学院讲师,主要从事应用数学及多元统计分析研究.

1672-2027(2015)01-0020-02

O173.2

A