鲁棒控制器在网络控制中的应用研究——基于改进人工蜂群优化方法设计

张 谦， 高容翔， 温盛军， 梁建勋

(中原工学院，郑州 450007)

鲁棒控制器在网络控制中的应用研究
——基于改进人工蜂群优化方法设计

张 谦， 高容翔， 温盛军， 梁建勋

(中原工学院，郑州 450007)

在设计H∞回路成形控制器并将其应用于网络温度控制系统时，权函数参数的选择十分关键。但在寻找满足设计要求的权函数参数过程中，用传统的人工蜂群算法会出现收敛速度过慢、容易陷入局部最优等问题。基于此，本文对传统的人工蜂群算法进行了改进，用改进后的人工蜂群算法进行了控制器的设计。实验结果表明，改进算法之后设计的控制器不仅能够保证网络温度控制系统稳定在平衡位置，而且控制效果更好。

H∞回路成形控制器；网络温度控制系统；改进的人工蜂群算法

随着计算机网络和通信技术的不断发展，网络控制系统得到了越来越多的应用,也有越来越多的专家和学者对网络控制系统做了更加深入和详细的研究。Tran H D等[1]提出了网络控制中PID参数自整定方法并设计了一种自适应PID控制器；张谦等[2]提出了一种基于CGT模型输出跟随控制的模型；尹勇等[3]将模糊PID算法应用于网络控制系统中。然而以上控制方法仅考虑了在网络控制系统存在时延情况下如何保证被控对象稳定，并没有考虑网络系统中可能出现的噪声和干扰。H∞控制器是一种鲁棒控制器，对外界的干扰有很好的抑制作用。本文引入了H∞回路成形控制器，确保被控系统在受到外界环境干扰的情况下依然可以回到期望的平衡位置。针对控制器参数的选择问题，李建等[4]通过粒子群算法与H∞混合灵敏度算法相结合设计控制器来实现对飞行系统的稳定控制，何海娟等[5]将粒子群算法应用于H2/H∞鲁棒控制器设计。本文通过引入差分进化算法和模拟退火理论改进传统人工蜂群算法，保证了寻优得到的控制器参数是最优的。仿真实验表明，通过改进人工蜂群算法设计的控制器能够保证网络温度控制系统在外界干扰的情况下依然能够稳定运行。

1 网络温度控制系统模型

铂尔贴作为一种高效的制冷装置已经被应用于冰箱等家用电器中。本文选用铂尔贴作为执行器对铝板进行制冷，并通过温度传感器实时采集温度信息。网络温度控制系统的模型如图1所示。

图1 基于铂尔贴的网络温度控制系统

控制器到执行器之间的网络传输时延为e-s τca，反馈回路的网络传输时延为e-s τcs。网络通信采用时间驱动的原则，这样,当一次网络通信中的传输时间τ大于采样周期T时会产生网络中的通信时延。网络中的通信时延与具体的网络结构有关。喻寿益等提出了解决网络随机时延的方法[6]。本文则针对文献[2]中的网络平台，将网络中的通信时延定义为τ=τca+τcs=19 s。将铂尔贴和铝板作为广义被控对象G(s)，并通过系统辨识的方法[7-8]建立被控对象的数学模型：

(1)

由式(1)可知,系统的极点为-0.006 2，极点小于0，被控对象本身是稳定的。

2 H∞回路成形控制器

H∞回路成形理论的基本原理是引入预补偿器W1和过补偿器W2成形开环回路奇异值曲线，使成形后的开环回路奇异值曲线满足以下系统性能要求。

(1) 设计权函数W1和W2成形被控对象G的奇异值曲线，成形后的对象Gs=W1GW2，如图2所示。

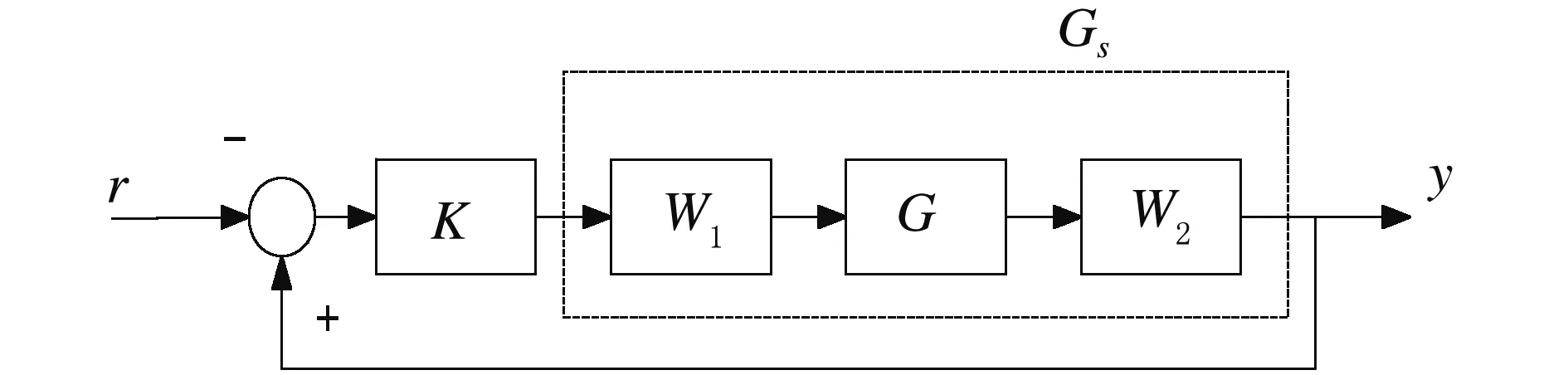
图2 被控对象奇异值成形图

Gs满足奇异值曲线在低频段尽可能大、在高频段尽可能小，穿越频率尽可能大且能够平滑转换的要求，如图3所示。

图3 开环奇异值成形图

(2)求解控制器K，使整个闭环系统的传递函数F满足式(2)[9-10]：

‖F‖∞<γ

(2)

这里γ是定义的鲁棒稳定性边界。整个闭环控制系统如图4所示。其中：w为外部输入信号；u为控制输入信号；y为观测信号；z为被控输出信号。

图4 基于网络的H∞鲁棒控制系统模型图

(3)合成控制器Kf=W2KW1，如图5所示。

图5 合成控制器

3 改进的人工蜂群算法

3.1 传统人工蜂群算法

传统人工蜂群算法寻找最优解的步骤如下：

(1)首先由称之为引领蜂的蜜蜂开采食物源，食物源代表可优化的解。食物源初始化公式为：

Xi,j=Xmin,j+rand(0,1)(Xmax,j-Xmin,j)

(3)

其中:Xmax,j和Xmin,j是可选的食物源范围;rand(0,1)表示在0～1之间生成的一个随机数;Xi,j是食物源。

之后引领蜂在食物源周围寻找新的食物源并进行开采。新食物源开采公式为:

Vi,j=Xi,j+φi,j(Xi,j-Xk,j)i≠k

(4)

其中:Vi,j代表一个新的食物源;k是在1～SN之间生成的一个随机数;SN是食物源的数量;φi,j是在-1～1之间生成的一个随机数。

食物源质量的好坏通过适应值表示，引领蜂在开采新的食物源后通过适应值比较食物源的优劣。如果新的食物源适应值优于原有的食物源，则保存该食物源，否则丢弃该食物源。定义适应值，如式(5)：

(5)

其中:fi是第i个食物源对应的优化问题的目标函数值;Fitnessi表示第i个食物源的适应值。

(2)引领蜂将开采得到的食物源信息与跟随蜂通过跳摇摆舞的方式进行共享。跟随蜂通过式(6)的概率公式选择食物源：

(6)

其中:fiti表示第i个食物源的适应值；SN是食物源的个数；Pi是第i个食物源被选择的概率。

跟随蜂选择引领蜂后就确定了要开采的食物源，依据式(4)在已有食物源周边进一步寻找新的食物源。

(3)在经过了limit代寻优之后，如果食物源依旧没有更新，该食物源有可能已经陷入到局部最优，这时要放弃该食物源，由称为侦查蜂的蜜蜂依照式(3)重新选择新的食物源。

3.2 改进的人工蜂群算法

针对传统人工蜂群算法存在收敛速度慢、容易陷入局部最优的缺点，本文通过差分进化算法[11-12]和模拟退火算法[13-14]两种优化搜索机制来改善算法的性能。

差分进化算法是一种随机并行直接搜索算法，利用种群中两个随机选择的不同向量来干扰一个现有向量。通过把种群中两个成员之间的加权差向量加到第三个成员上来产生新的向量。引领蜂在食物源周围寻找新的食物源时，采用式(7)开采新的食物源:

Vn=Xa+ξ(Xb-Xc)

(7)

其中：Xa、Xb、Xc表示已经开采的食物源；Vn是新开采的食物源，n不等于a、b、c；ξ是在0～1之间生成的一个随机数。

模拟退火算法是一种启发式随机搜索方法，在每一代引领蜂或跟随蜂搜索最优解的过程中，运用模拟退火算法不仅能保存适应值好的食物源，适应值比较差的食物源也可以以一定的概率保留下来。引领蜂在搜索得到新的食物源后，通过公式(8)可得到新食物源的接收概率：

(8)

其中：fitnesso是原有食物源的适应值；fitnessn是新食物源的适应值；prob是接收概率；T是常数。定义T，如式(9)：

T=T0βiter

(9)

其中：T0是初始值；β是设定的常数；iter是迭代次数。

4 H∞回路成形控制器设计

定义控制器权函数如式(10)：

(10)

其中,a、b、c、d、e、f是待优化的参数。

通过改进的人工蜂群算法寻优权函数参数。其中寻优600代，一共30个食物源，每个食物源对应6个待优化的参数。以每一代寻优得到的结果加入奇异值约束，使奇异值满足H∞回路成形控制器设计要求。以被控系统输出信号z的阶跃响应超调量和调节时间作为目标函数值。为了更好地反映权函数的选择对控制器设计的影响，本文对阶跃响应超调量和调节时间进行加权，得到一个综合目标函数值。定义阶跃响应超调量σm和调节时间tm的权重各为50%，则第i个食物源的综合目标函数值为：

fi=0.5σm+0.5tm

(11)

5 仿真实验分析

通过改进的人工蜂群算法寻优控制器权函数，适应值变化曲线如图6所示。

图6 适应值变化曲线图

此时，可以得到满足控制器设计要求的最优解：a=10.776，b=0.139，c=8.163，d=5.3，e=0.002 5，f=0.02。对应的权函数如式(12)：

(12)

此时，被控对象的奇异值曲线如图7所示。

成形的开环回路奇异值曲线能够满足在低频段比成形前的高，在高频段比成形前的低，穿越频率比成形前的大。合成的控制器Kf为：

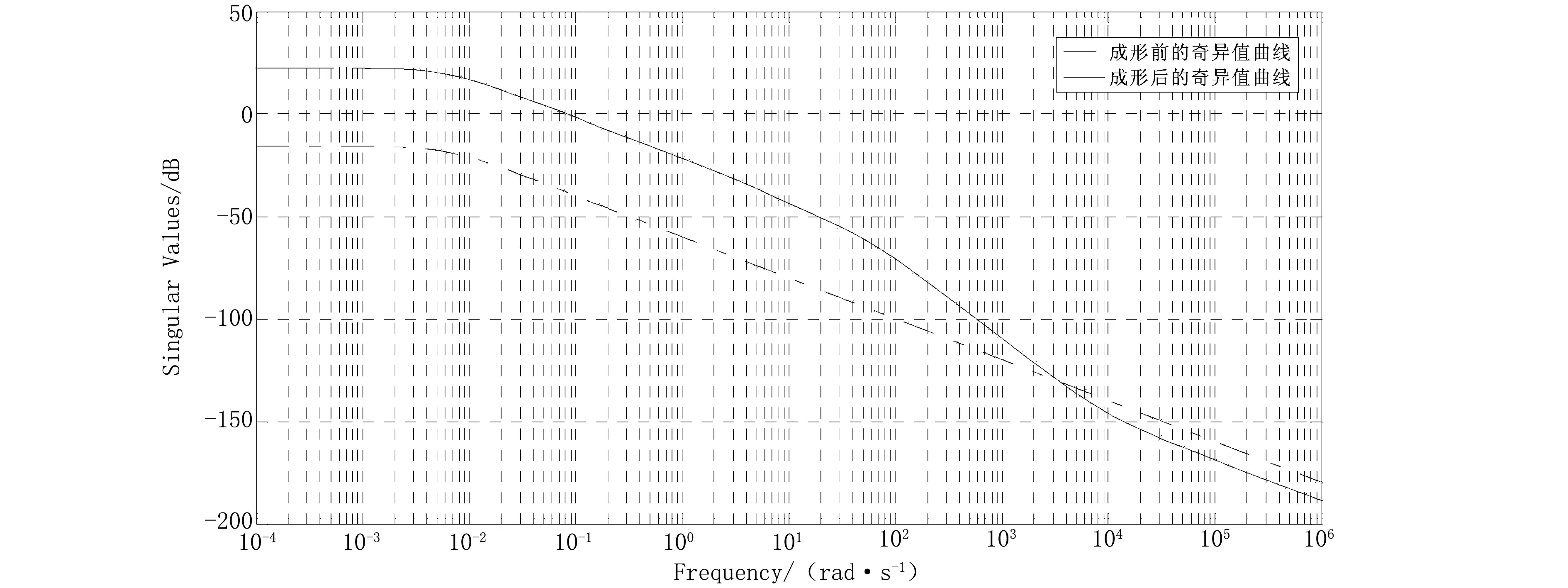
图7 被控对象开环奇异值曲线

(13)

t=7 s时，在网络控制系统的控制器到执行器之间加入阶跃扰动信号，通过H∞回路成形控制器控制系统所得到的系统输出如图8所示。

t=10 s时，在网络温度控制系统的反馈回路中加入高频噪声干扰，通过H∞回路成形控制器控制系统所得到的系统输出如图9所示。

从图8和图9可以看出， 回路成形控制器在被控系统中存在阶跃扰动和高频噪声的情况下依然可以保证系统的稳定性。相比于改进的人工蜂群算法，传统人工蜂群算法寻优得到的控制器响应超调量较大，调节时间也更长。

图8 存在阶跃扰动的网络温度控制系统阶跃响应曲线

图9 存在高频噪声的网络温度控制系统阶跃响应曲线

6 结 语

本文以网络温度控制系统为研究对象，通过H∞回路成形方法设计出一个稳定的鲁棒控制器，并采用改进的人工蜂群算法优化该控制器参数。仿真结果表明，该控制器可以使系统在受到外界扰动时依然保持在平衡状态，并且改进的人工蜂群算法可以使系统的输出响应更快，超调量更小。

[1] Tran H D，Guan Z H. A Normalized PID Controller in Networked Control Systems with Varying Time Delays[J].ISA Transactions,2013(52):592-599.

[2] 张谦，李红军，温盛军，等. 基于HORB的网络化温度控制系统设计与实现[J].郑州大学学报，2014,35(3):82-85.

[3] 尹勇，李少芳，王吉红. 模糊PID算法在网络控制系统中的应用[J].武汉理工大学学报，2010,32(6):144-148.

[4] 李建，章卫国，李广文. 基于粒子群算法的H∞鲁棒飞行控制系统设计[J].弹箭与制导学报，2008,28(1):131-134.

[5] 何海娟，张凌波，顾幸生. 基于多目标粒子群算法的H2/H∞鲁棒控制设计[J].华东理工大学学报，2011,37(1):100-104.

[6] 喻寿益，陈学一. 存在随机延时的网络控制系统的性能分析[J].中南大学学报，2008,39(4):799-804.

[7] 高思，康静秋，杨振勇，等. 基于递推最小二乘法的主蒸汽温度控制系统系统辨识与优化[J]. 热力发电，2011,40(6):29-33.

[8] 仇振安，何汉辉. 基于广义最小二乘法的系统模型辨识及应用[J]. 计算机仿真，2007,24(10):89-92.

[9] Patra S，Sen S，Ray G. Design of Static H∞Loop Shaping Controller in Four-block Framework Using LMI Approach[J]. Automatica，2008,44(8):2214-2220.

[10] Patra S，Sen S，Ray G. A Linear Matrix Inequality Approach to Parametric H Loop Shaping Control[J]. Journal of the Franklin Institute，2011,348(8):1832-1846.

[11] 姚峰，杨卫东，张明，等 改进自适应变空间差分进化算法[J]. 控制理论与应用，2010,27(1):32-38.

[12] Guo H X，Li Y N，Li J L. Differential Evolution Improved with Self-adaptive Control Parameters Based on Simulated Annealing[J]. Swarm and Evolutionary Computation，2014(19):52-67.

[13] 孙年芳. 基于遗传模拟退火算法的约束求解研究[D].长沙：湖南大学，2010.

[14] Wang W L，Tang M H. Simulated Annealing Approach to Solve Nonogram Puzzles with Multiple Solutions[J]. Computer Science，2014(36):541-548.

(责任编辑：张同学)

The Research of Robust Controller in Network Control——Based on Improved Artificial Bee Colony Optimization

ZHANG Qian， GAO Rong-xiang， WEN Sheng-jun， LIANG Jian-xun

(Zhongyuan University of Technology, Zhengzhou 450007, China)

Selecting the appropriate weight function parameters is very important for designing loop shaping controller to apply to network temperature control system. But slow convergence speed and easily plunged into local optimum is disadvantages of traditional artificial bee colony algorithm for looking for the requirement weight function parameters. So traditional artificial bee colony algorithm is improved. The parameters of weight function which is got by improved artificial bee colony algorithm can ensure the better controller performance. The experiment results show that controller is designed by improved artificial bee colony algorithm not only keep network temperature control system stability in the equilibriumposition, but also get better result compare to traditional artificial bee colony.

loop shaping controller; network temperature control system; improved artificial bee colony algorithm

2015-05-13

张谦(1957-)，男，河南平顶山人，教授，硕士，主要研究方向为智能控制理论与嵌入式系统应用。

1671-6906(2015)06-0065-05

TP273

A

10.3969/j.issn.1671-6906.2015.06.015