智能车辆纵向运动模型的反馈线性化及控制
2015-03-03房泽平段建民
房泽平, 段建民
(1.北京工业大学 北京市交通工程重点实验室,北京 100124;2.中原工学院, 郑州 450007)
智能车辆纵向运动模型的反馈线性化及控制
房泽平1,2, 段建民1
(1.北京工业大学 北京市交通工程重点实验室,北京 100124;2.中原工学院, 郑州 450007)
针对智能车辆纵向运动模型的本质非线性控制设计问题,提出采用反馈线性化方法得到其线性化模型,利用状态反馈阵(SFM)算法进行纵向运动控制。对智能车辆的纵向运动动力学方程,分别采用全状态线性化和输入-输出线性化方法,得到其线性状态空间模型。在Matlab/Simulink环境下,构建了基于SFM算法的智能车辆纵向运动控制仿真模型,输入阶跃和正弦信号后得到了速度和位置的控制仿真结果。结果表明,输入-输出线性化方法和SFM算法适用于对智能车辆的纵向运动控制。
智能车辆;纵向运动;反馈线性化;状态反馈阵
智能车辆作为智能交通系统的关键技术之一,是许多高新技术综合集成的载体。智能车辆能自动地全部或部分完成一项或多项驾驶任务。智能车辆自动完成驾驶任务,特别是纵向运动控制能够提高车辆的道路适应能力,改善行车安全,降低环境影响[1-2]。针对智能车辆纵向运动控制的研究,文献[3]建立了智能车辆纵向控制线性模型和采用专家控制规则的PID自适应控制算法。文献[4]和文献[5]建立了智能车辆纵向控制的非线性模型,探讨了自适应控制算法及滑模变结构控制算法的应用。研究表明,智能车辆纵向控制模型具有严重的本质非线性[6]。采用非线性状态变换、非线性反馈变换将非线性系统转化为线性系统的理论和方法,为非线性控制系统提供了一种综合方法。反馈线性化方法是解决具有大范围非线性特性的控制对象控制问题的一种有效方法[6-7]。
本文针对智能车辆纵向运动模型的本质非线性问题,验证该非线性模型的可反馈线性化,并采用状态空间的全状态线性化和输入-输出线性化方法得到其线性化状态空间方程,然后用状态反馈阵(SFM)算法对变换后的线性系统进行纵向控制设计,在Matlab/Simulink环境下,构建了基于SFM算法的智能车辆纵向运动控制仿真模型,分别给出了以阶跃和正弦信号输入、速度和位置输出的仿真结果。仿真结果表明,将反馈线性化方法和SFM算法用于智能车辆的纵向运动控制是可行的。
1 智能车辆纵向运动模型
车辆纵向动力传动系统包括发动机、液力变矩器、传动系及车轮等,各部分通过力矩和转速传递连接。各部分的特性参数及相互间的动力传递如图1 所示。

图1 智能车辆纵向运动模型(驱动)
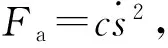
(1)
纵向轮胎力Ftf是驱动车辆前进的主要动力。在纵向滑移率i很小而且车辆正常行驶的情况下,纵向轮胎力Ftf与滑移率i的关系为:
Ftf=Ki·i
(2)
其中,Ki是轮胎刚度。
2 纵向运动模型反馈线性化
车辆纵向运动模型(式(1))是严重非线性的[6]。反馈线性化方法是解决具有大范围非线性特性的控制对象控制问题的一种有效方法。其设计思想是通过恰当的非线性状态反馈和非线性坐标变换或动态补偿,将一个非线性系统变换成部分或全部线性系统,然后用线性系统设计方法对变换后的线性系统进行设计,使系统满足设计指标的要求[9]。
2.1 可反馈线性化条件
对于单输入单输出系统,当且仅当定义域D0⊂D,使得
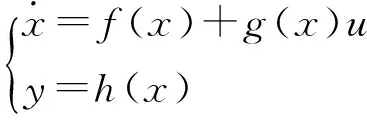
(3)

2.2 全状态线性化模型一
2.2.1 可反馈线性化验证
(4)
由式(3)可得:
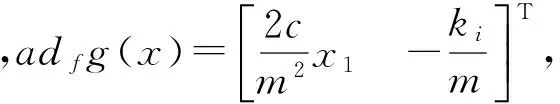
对于所有x,rankG(x)=2,满足条件a。又因为,分布D=span{g}是对合的,满足条件b。因此,综合条件a验证和条件b验证,式(4)可反馈线性化。
2.2.2 确定h(x)

式中,Lfh表示对函数f和函数h进行李运算。
这样,h(x)一定与x1无关。因此,Lfh(x)=
因此,可取y=h(x)=x2,则式(4)变换为:
(5)

(6)
2.3 全状态线性化模型二
(7)
经过推导,可确定y=h(x)=x1,则式(7)状态反馈线性化为:
(8)
2.4 输入-输出线性化模型
输入-输出线性化指通过构造稳定的状态反馈控制律,使得闭环系统具有理想的线性输入-输出特性。
(9)
式(9)的相对阶r为1,即r 又因为 对于所有x,矩阵G(x)的秩为2。显然,分布D=span{g}是对合的。因此,满足可反馈线性化条件a和条件b,式(9)可反馈线性化。 取μ1=h(x)=x2。由李导数Lgφ1= 这样,φ1(x)中一定不能出现x2,所以,这里取φ1(x)=x1。则式(9)的规范化形式为: 式(8)变换的相应状态方程为: (10) (11) 2.5 模型分析 由全状态线性化方法得到的模型式(6)和式(8)的状态变量均为位置和速度,仅是符号表示上的区别。式(6)和式(8)的输出均为智能车辆的位置。由输入-输出线性化方法得到的模型式(11)的状态变量为速度和位置,式(11)的输出为智能车辆的速度。因此,对于智能车辆纵向控制的位置和速度,可以根据要求,从式(6)、式(8)和式(11)中选择不同的状态方程。这进一步表明,应结合实际物理意义选择非线性系统的线性化状态方程的状态变量和系统输出形式。 3.1 状态反馈阵(SFM)算法控制器设计 针对式(6),可设计一个稳定的线性状态反馈控制律v=-k1·x1-k2·x2。 从配置闭环期望极点z1,2=-1±j,求得k1=k2=2,则式(6)的整个状态反馈控制律为: 同理,可得到式(8)的整个状态反馈控制律: 同理,也可得到式(11)的整个状态反馈控制律: 3.2 仿真模型 根据式(1)和相应的状态反馈控制律,在Matlab/Simulink环境下构建的仿真模型如图2所示。 图2 仿真模型 3.3 仿真结果 3.3.1 位置控制仿真结果 取m=800kg,μ=0.01,c=0.5kg/m,ki=3 700N[11]。采用式(6)的线性化模型,基于状态反馈阵算法的位置控制仿真结果如图3所示。在图3(a)中,输入信号为位置sref阶跃信号。在0时刻,给定位置sref为5m,在3s附近位置输出s稳定在5m。在4s时刻,给定位置sref为10m,在6s附近位置输出s稳定在10m。曲线i为整个状态反馈控制律的输出。曲线u为状态反馈控制律的输出,其输出随着输入sref的变化而时刻进行补偿,使系统的位置输出s跟踪其输入的变化。图3(a)表明状态反馈阵算法对阶跃输入具有较好的控制能力。在图3(b)中,输入信号为位置sref的正弦信号,位置输出s不能跟踪给定位置输入sref,表明状态反馈阵算法对正弦输入信号的控制性能较差。 3.3.2 速度控制仿真结果 参数取值同3.3.1,采用式(11)的线性化模型,基于状态反馈阵算法的速度控制仿真结果如图4所示。由图4可以看出,对于给定速度的阶跃和正弦输入,经过初始时刻的短暂调节,速度输出能跟踪给定输入。 (b)正弦输入结果 (a)阶跃输入结果 (b)正弦输入结果 对智能车辆纵向运动模型进行反馈线性化,针对得到的线性化方程设计了基于SFM算法的控制器,以完成对智能车辆的速度和位置控制。采用全状态线性化方法得到的线性化模型被用于智能车辆的位置控制。采用输入-输出线性化方法得到的线性化模型被用于智能车辆的速度控制。在Matlab/Simulink环境下,构建了基于SFM算法的纵向运动控制仿真模型,得到了阶跃输入和正弦输入的速度及位置输出的仿真结果。仿真结果表明,采用不同的线性化方法得到的线性化模型,对于不同的输入信号,可得到不同控制性能的结果。这进一步表明,采用输入-输出线性化的反馈线性化方法和SFM控制算法,对于智能车辆的纵向运动控制具有较好的性能。因此,本文采用反馈线性化方法和SFM算法的方案对于智能车辆纵向运动控制是可行的。 [1]TsugawaS.AnOverviewonEnergyConservationinAutomobileTrafficandTransportationwithITS[C]//Proc.ofIEEEInternationalVehiclesElectronConference.Piscataway:IEEEpress, 2001: 137-142. [2] 秦贵和, 葛安林, 雷鱼龙. 智能交通系统及其车辆自动控制技术[J]. 汽车工程, 2001, 23(2): 92-96. [3] 辛建国, 李果, 丁华荣.汽车自动驾驶纵向控制技术的研究[J]. 计算技术与自动化, 1995, 14(3): 13-17. [4]ChoiS.DesignofaRobustControllerforAutomotiveEngines:TheoryandExperiment[D].Berkeley:UniversityofCalifornia, 1993. [5]BartoliniG,FerraraA,PisuP.LongitudinalControlDesignofPassengerVehicleswithSecondOrderSlidingModes[C]//ProceedingsoftheAmericanControlConference.Piscataway:IEEEPress, 2000, 1(6): 120-124. [6]McmahonDH,NarendranVK,SwarD,etal.LongitudinalVehicleControllersforIVHS:TheoryandExperiment[C]//Proc.ofthe1992AmericanControlConference.Piscataway:IEEEPress, 1992:1753-1757. [7]ChengDZ,LiZQ.ASurveyonLinearizationofNonlinearSystems[J].JournalofShandongUniversity(EngineeringScience), 2009, 39(2): 26-36. [8] 詹军. 用于自适应巡航控制的汽车纵向动力学模型的建立[J]. 吉林大学学报, 2006, 36(2): 157-160. [9] 宾洋, 李克强, 连小珉. 低速行驶车辆的非线性系统建模及控制[J]. 控制理论与应用, 2005, 22(5): 814-819. [10] 朱义胜, 董辉, 李作洲. 非线性系统(第三版)[M]. 北京:电子工业出版社, 2011. [11]DanieleC,MirceaL.AHybridMPCApproachtotheDesignofaSmartAdaptiveCruiseController[C]//Proceedingsofthe2006IEEE,InternationalConferenceonControlApplications.Piscataway:IEEEPress, 2006: 231-236. (责任编辑:王长通) Feedback Linearization and Control of Longitudinal Motion for Intelligent Vehicle FANG Ze-ping1,2, DUAN Jian-min1 (1. Beijing Key Laboratory of Traffic Engineering, Beijing University of Technology, Beijing 100124;2.Zhongyuan University of Technology, Zhengzhou 450007, China) In this paper, considering the fact that longitudinal motion model of intelligent vehicle established is nonlinear, a feedback linearization method is proposed to obtain its linear model. The state feedback matrix (SFM) algorithm is used to control intelligent vehicle. The longitudinal dynamic equations of intelligent vehicle is linearized by using full state linearization and input-output linearization method to obtain its linear state-space equation, respectively. In the Matlab/Simulink environment, simulation model is constructed based on SFM algorithm. Under the step and sinusoidal signal input, the simulation results of speed and position are obtained. Simulation results show that the input-output linearization method and SFM algorithm have better performance to longitudinal motion control of intelligent vehicle. intelligent vehicle; longitudinal motion; feedback linearization; state feedback matrix 2015-04-25 北京市属高等学校人才强教计划资助项目(038000543115025) 房泽平(1975-),男,辽宁开原人,讲师,博士生,主要研究方向为智能车辆应用技术。 1671-6906(2015)06-0010-05 TP271.62 A 10.3969/j.issn.1671-6906.2015.06.003
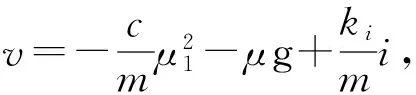
3 纵向运动控制仿真研究




4 结 语
