一种3R1P机械臂的运动学建模及实验分析

李 峰 ， 岳 云

(1．中原工学院信息商务学院；2．CATERPILLAR(郑州)有限公司， 郑州 450007)

一种3R1P机械臂的运动学建模及实验分析

李 峰1， 岳 云2

(1．中原工学院信息商务学院；2．CATERPILLAR(郑州)有限公司， 郑州 450007)

运用D-H方法和运动学原理首次得到了3R1P机械臂的运动方程，建立了3R1P机械臂的运动学模型。通过仿真实验和机械臂的HEBB神经网络控制运行实验验证了系统的稳定性，以及系统建模和HEBB神经网络控制的合理性和有效性，建立了3R1P机械臂的HEBB自适应神经网络系统框图，提出了平稳3R1P机械臂运行的策略，缩短了3R1P机械臂的研发周期。

D-H方法；3R1P机械臂；运动方程； HEBB神经网络

机器人是衡量一个国家科技创新、高端制造业水平的重要标志。当前，提高机械臂运行平稳性，完善机械臂运行的自适应性，增强机械臂的定位精度，抑制其弹性振动是一项具有挑战性的课题[1]。

3R1P机械臂作为机器人应用平台，具有通用性强、结构紧凑、可控性强的优势。本文通过运动学分析了解机械臂的运动学原理，运用Motion Simulation软件对所研发的3R1P机械臂建模，并进行运动学仿真；通过软件仿真和实验，得到相关实验数据，验证系统的合理性和有效性，提高定位精度；对3R1P机械臂进行HEBB神经网络控制，得到机械臂的控制方法，并通过不断调试优化控制方法，提高运行精度。本文试图完善3R1P类机械臂的结构设计和运行控制方法，缩短3R1P类机械臂的研发周期。

1 3R1P机械臂的运动学分析

1.1 姿态变化关系

图1是用D-H法建立的机械臂运动学简图。各连杆通过关节连接在一起，各个关节有移动副也有转动副，其中3个转动副分别为0、1、2，一个移动副(关节)为3，各个杆件坐标系的Z轴方向与关节轴线重合。对于移动关节3，Z轴线为此关节移动方向[2]。

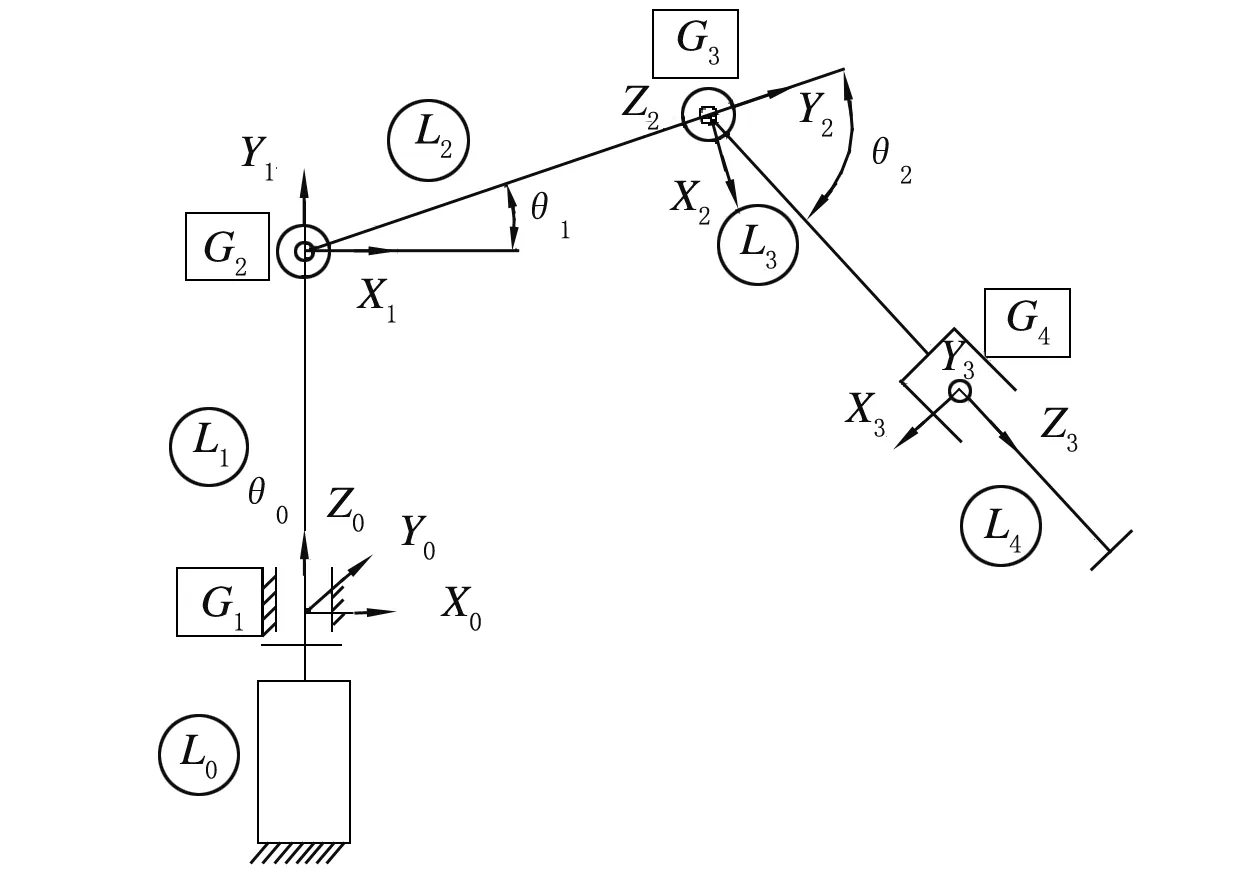
图1 3R1P机械臂运动学简图

1.1.1 D-H坐标系的建立

由图1可知，X为连杆轴线，朝外指向目标;Z为转动关节的轴线，为法向矢量;Y为姿态矢量。

1.1.2 各连杆的D-H参数和关节变量

对于建立的连杆坐标系，可用4个参数来描述：两关节之间的连杆长度为a，连杆扭角为α，两连杆之间距离为d，两连杆夹角为θ。在转动关节中，θ为关节变量，其他3个参数不变。对于移动关节，d是关节变量，其他3个参数不变[3]。实验采用3R1P机械臂的D-H参数见表1。

表1 3R1P机械臂的D-H参数

根据表1所示的D-H参数和齐次变换矩阵公式,可求得从连杆i到连杆i-1的坐标变换矩阵Ai：

Ai=Rot(Z,θi)Trans(0,0,di)Rot(X,αi)

其中：L1向L0的坐标变换矩阵为：

L2向L1的坐标变换矩阵为：

L3向L2的坐标变换矩阵为：

L4向L3的坐标变换矩阵为：

令3R1P机械臂运动方程的矩阵形式为：

则其中,n列参数值为：

nX=(cosθ0×cosθ1-sinθ0×sinθ1)(cosθ2×cosθ3-sinθ2×sinθ3)

nY=(sinθ0×cosθ1+sinθ1×cosθ0)(cosθ2×cosθ3-sinθ2×sinθ3)

nZ=-sinθ2×cosθ3-cosθ2×sinθ3

O列参数值为：

oX=(-cosθ0×sinθ1+sinθ0×cosθ1)×cosθ2

oY=(sinθ0×sinθ1+cosθ0×cosθ1)×cosθ2

oZ=0

m列参数值为：

mX=(cosθ0×cosθ1-sinθ0×sinθ1)(cosθ2×sinθ3-sinθ2×cosθ3)

mY=(sinθ0×cosθ1+cosθ0×sinθ1)(cosθ2×sinθ3-sinθ2×cosθ3)

mZ=-sinθ2×sinθ3-cosθ2×cosθ3

p列参数值为：

pX=a2(-sinθ1×cosθ0+cosθ1×sinθ0)×cosθ2

pY=a2(sinθ1×sinθ0-cosθ1×cosθ0)×cosθ2

pZ=0

求得3R1P机械臂运动方程，使该类机械臂的运动学建模及结构设计更为便捷，可有效降低研发时间，提高机械臂的设计精度和质量。

1.2 自然作业姿态动作的设计流程

由于机械臂的通用性，机械臂的结构尺寸已被限制，机械臂的动作环境被大体确定。在确定的环境内要实现特定的功能或达到指定的位置，需要对机械臂的控制系统进行智能化处理，要建立机械臂各关节、各动力源、各接触环节之间的定位关系，并判别它们的定位准确度。机械臂设计流程模型具有许多形式，典型的一种是多层前馈网络，即HEBB神经网络(见图2)[4-5]。该网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型。应用该网络不仅可以最大限度地减少控制过程中出现的错误，还可以不断地自行优化运行参数[6-7]。

图2 HEBB神经网络

运用HEBB神经网络控制，通过指导者一次(或多次)示范，学习者多次记录、调整优化各运动的定位函数、定位参数，控制3R1P机械臂的动作幅度、动作时间以及各姿态动作的协调程度，以优化3R1P机械臂的姿态，使机械臂顺利完成定位及精度的判别等。机械臂通过自适应性神经网络控制系统可完成信息处理，与各从动系统进行信息交换，学习、感应、判断、指导各关节和可编程开关量状态数据处理(包括启动信号、各轴传感器信号、可编程开关量等)[8]。图3为运用HEBB神经网络控制的控制图。

图3 HEBB神经网络控制图

2 作业姿态实验

受机械臂结构尺寸及能源使用局限性的影响，空间3R1P机械臂的设计与传统的机械臂设计相比更加注重产品的小功耗、轻质量、高效率，因此需要对机械臂的运动进行一系列优化设计，进而需要进行相关的建模分析及研发后相关动作的实验分析，找出问题及不足。

2.1 D-H法空间3R1P机械臂自然作业姿态仿真实验

三维软件建模以后，将数据导入Motion Simulation,分别设定机械臂3个转动副和1个移动副在各自坐标系里的运动方程。通过软件仿真，得到各个运动副在以地面为坐标系中的位移和速度曲线，如图4-图7所示。

(a)底座角位移

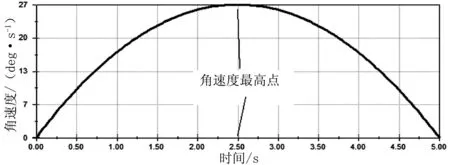
(b)底座角速度

(a)腕部角位移

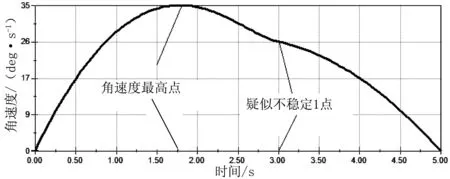
(b)腕部角速度

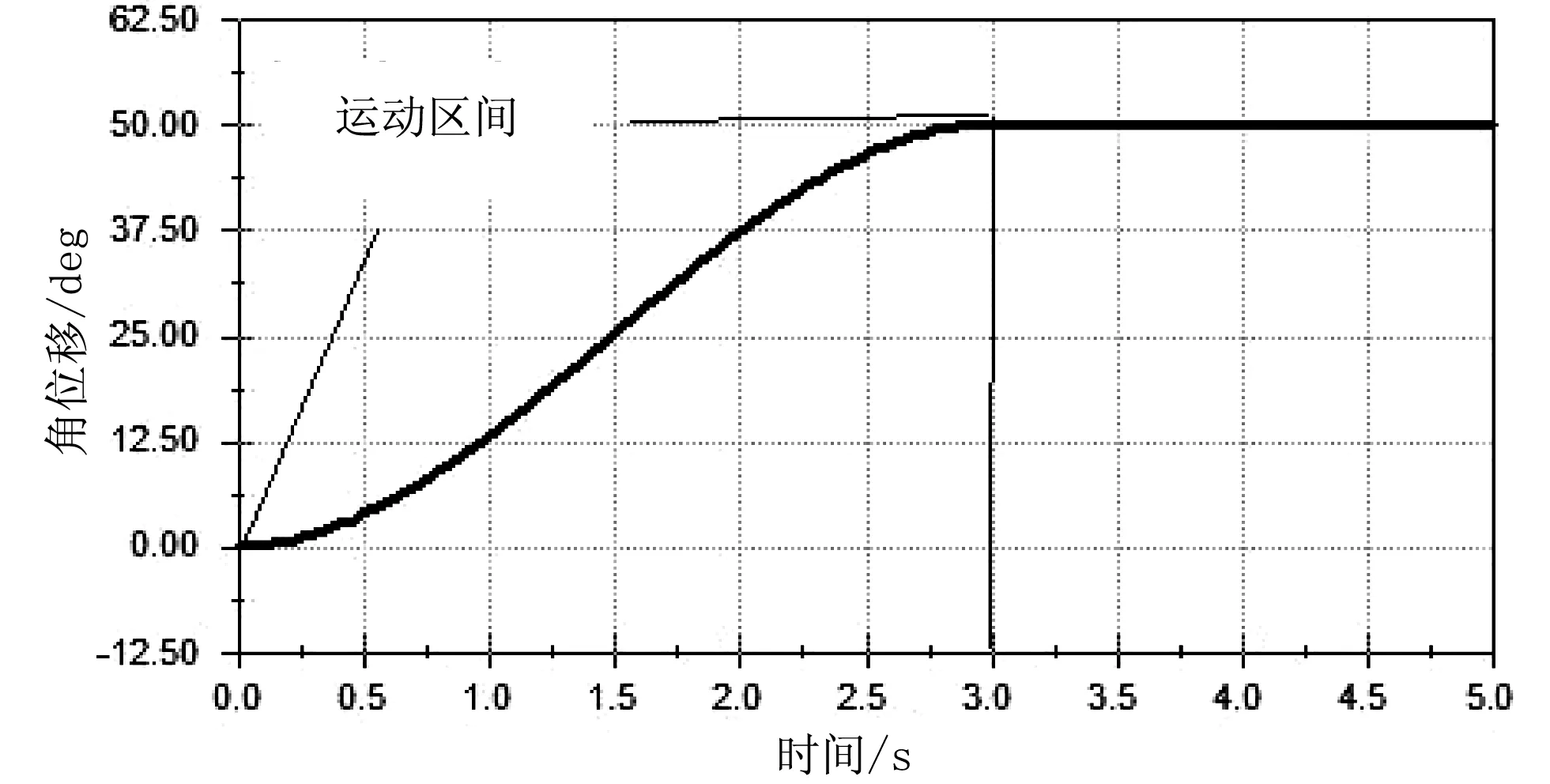
(a)臂部角位移

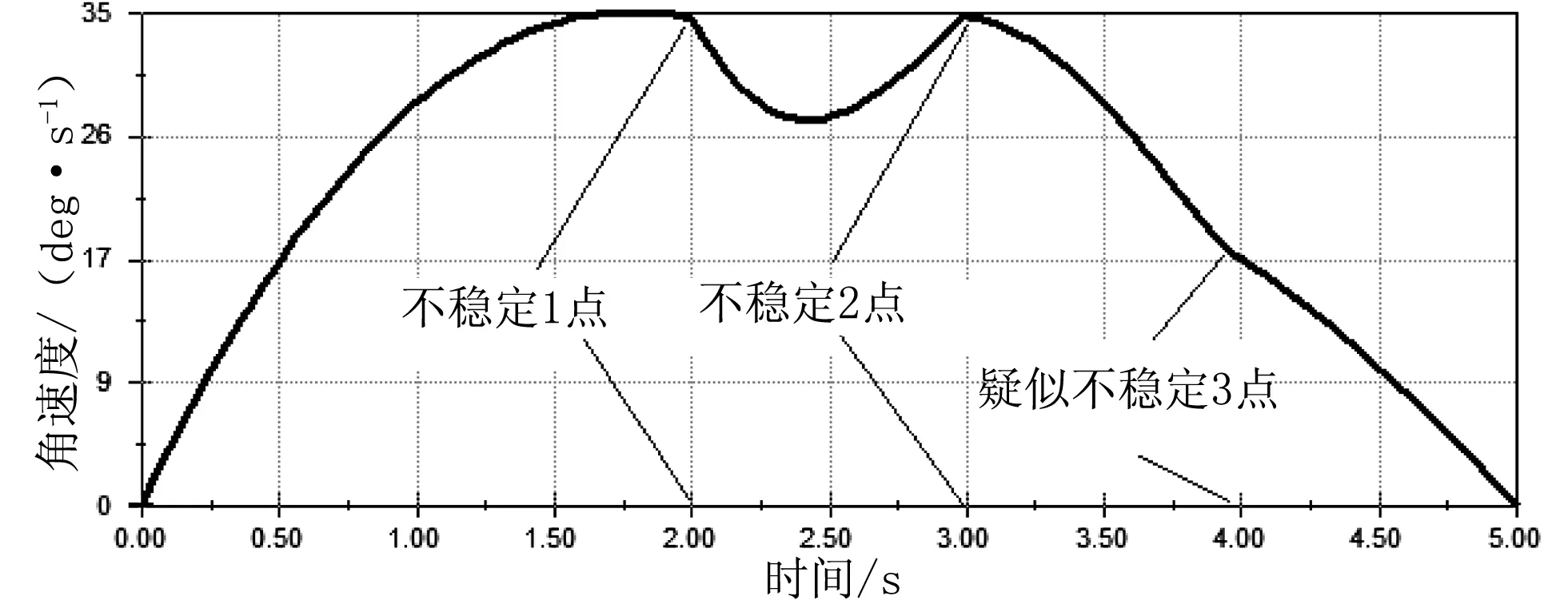
(b)臂部角速度

假定3R1P机械臂的接近运动是由静止状态从初始位姿向目标位姿运动，则运动过程有两个运动间距需要闭合，即位置间距和姿态间距。所设计的机械臂采用了点到点运动的轨迹规划，即它从起始点运动到终点，完成一定任务，点与点之间不存在任何的中间点，并且对于运动路径也没有设置要求，取运动时间为5 s,则由起始点到终点各个关节的旋转角度及位移分别见图4-图7。分析可知，机械臂前3个关节为旋转关节，第4个关节为直线自由度。在设计时，3R1P机械臂前3个关节的运动可以满足通常三自由度柱面坐标3R1P机械臂的运动要求，即机械手可以实现空间定位，第4个关节可以实现预定功能。该机械手使用第4个关节的位移完成相关执行任务[9]。图4(a)、图5(a)、图6(a)、图7(a)分别为底座、腕部、臂部关节和手部的运动位移。分析可知，各关节角位移、线位移是连续的，说明设计的动作是连续的、合理的。所设计的动作是底座、臂部、手部首先动作，时间点为0 s，腕部从2 s开始动作。在整个动作中，底座、手部连续运行5 s，腕部、臂部运行2 s后停止运行。动作速度变化平稳的是底座，如图4(b)所示，但腕部、臂部、手部的动作速度变化较大，如图5(b)、图6(b)、图7(b)所示。图5(b)、图6(b)中角速度变化时间点为2 s和3 s，图6(b)、图7(b)中角速度和线速度变化点除2 s、3 s外，在第4 s时也出现了较小的变化，究其原因为各个自由度的相互干涉。结合位移和速度推测，要保证各关节速度的平稳可采用两种方法：①保证各关节运行的同时性，即保持各关节运行时间均为5 s；②增加各关节的运行时间，以降低各关节的运行速度，使运动过程平稳。

在运动仿真的过程中，观察3R1P机械臂正常运动时各关节的运动情况(见图4-图7)，可以看到，各关节的运动轨迹是连续的，各连杆没有运动错位、突变的情况，从而验证了所有连杆参数的合理性。因此，3R1P机械臂各结构参数的设计能够满足定位功能要求[10]。

使用Motion Simulation不能使模型中各关节选取点的运动曲线在坐标系中显示，需要将Motion Simulation中各关节选取点运动曲线分别导出为运动参数。将运动参数输入MATLAB，得到图8所示的各关节上选取点以地面为坐标系的空间运动轨迹。

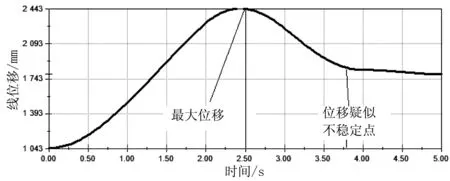
(a)手部线位移

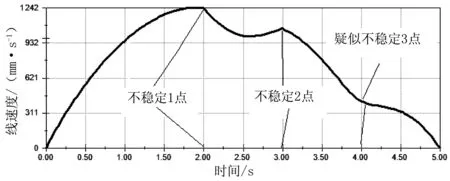
(b)手部线速度

从图8可以看出，3R1P机械臂手部、腕部、臂部由于同时动作，相互协调运行，因此，运动轨迹是空间曲线，且各关节在空间的运动轨迹平滑、协调，运动情况良好。这再次验证了3R1P机械臂设计参数的合理性[11]。通过观察机械臂各关节平面位移、速度曲线、空间位移曲线，可以很好地判定机械臂运动学模型建立的合理性和实际应用的可行性。利用这种方法设计3R1P机械臂的结构是高效的。

2.2 3R1P机械臂实验平台实验

可在3R1P机械臂实验平台上实现3R1P机械臂的HEBB自适应神经网络控制。将3R1P机械臂的运动限定在XYZ空间内，通过3R自由度实现机械臂手部运动位姿，能够以1P自由度实现手部功能。本文采用3R1P机械臂系统D-H法和内部HEBB神经网络引导策略进行实验，进行轨迹规划。将生成的中间点坐标和时间参数录入3R1P机械臂神经网络控制系统后，系统可通过感应，学习并控制3R1P机械臂的运行。

图9所示为机械臂控制系统框图。在指导者示教状态时，感应系统对各关节的运动位置和速度数据、各种输入和输出开关量进行采样及暂存，并进行相关分析，学习研究。在示教再现时，系统将处理过的数据发送给相关驱动器，实现其预定位置功能。由于系统采用了前馈加反馈的监督学习控制方法，可以不断调整，不断判断误差，不断改进，因此不仅可确保控制系统的稳定性和鲁棒性，而且可以有效提高系统的精度和自适应性。实际运行结果表明，采用HEBB神经网络控制的3R1P机械臂手部运动曲线平滑，运动过程平稳可靠。

(a)手部 (b) 腕部

(c)臂部 (d) 腰部

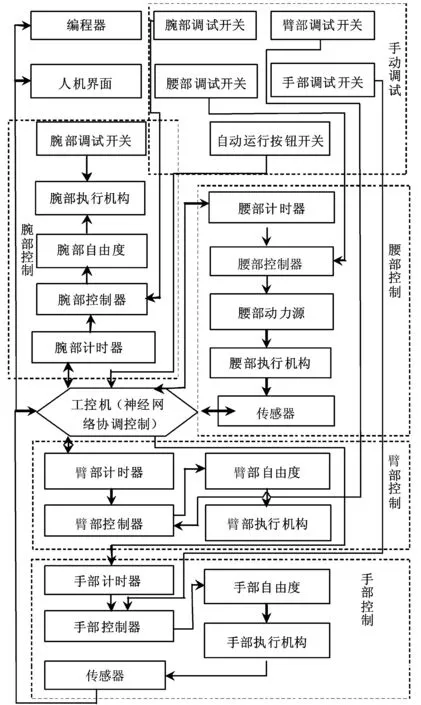
图9 3R1P机械臂控制系统框图

3 结 语

(1)本文构建了3R1P类机械臂的运动学模型，得到了3R1P类机械臂的运动学参数方程，方便了3R1P类机械臂的结构设计计算。

(2)通过研发3R1P机械臂，验证了3R1P机械臂的HEBB自适应神经网络系统框图，可为3R1P类机械臂的控制系统设计提供参考。

(3)通过D-H法的空间3R1P机械臂自然作业姿态仿真实验，得到了各关节的运动参数、平面和空间运动曲线，为进一步优化改进3R1P机械臂提供了新的依据。

(4)3R1P机械臂各自由度同时开始同时结束，并可延长各自由度运行时间，提高运行平稳性。

[1] Malekzadeh M, Naghash A, Talebi H A. A Robust Nonlinear Control Approach for Tip Position Tracking of Flexible Spacecraft[J].IEEE Transactions on Aerospace and Electronic Systems, 2011，47(4): 2423-2434.

[2] Wang J S, Liu X J, Wu C. Optimal Design of a New Spatial 3-DOF Parallel Robot with Respect to a Frame Free Index[J]. Science in China Series E: Technological Sciences, 2009,52(4):986-999.

[3] 刘极峰.机器人技术基础[M].北京：高等教育出版社，2006.

[4] Yuan Z R, Guo X G. Back Propagation Neural Networks for the Inverse Control of Discrete[J]. Advances in Modeling & Analysis, 1994, 40(4):13-23.

[5] Akhyar S, Omatu S. Neuromorphic Self-tuning PID Controller[C]//IEEE International Conference on Neural Networks. Piscataway: IEEE Press, 1993: 552-557.

[6] 沈柏桥,潘海鹏. BP网络智能PID控制算法在交流调速系统中的应用[J]. 电机与控制学报,2007，11(14):412-416.

[7] Yuan Z G, Guo X G. Back Propagation Neural Networks for the Inverse Control of Discrete Time Nonlinear Plant [J]. Advances in Modeling & Analysis, 1994, 40(4): 13-23.

[8] Liu S Y, Wang G R, Zhang H, et al. Design of Robot Welding Seam Tracking System with Structured Light Vision [J]. Chinese Journal of Mechanical Engineering, 2010, 23(4):436-442.

[9] Meng C, Wang T M, Guan S G, et al. Design and Analysis of Gecko-like Robot [J]. Chinese Journal of Mechanical Engineering, 2011,24(2):224-236.

[10] 罗家佳，胡国清. 基于matlab的机器人运动仿真研究[J]. 厦门大学学报(自然科学版),2005,44(5):640-644.

[11] 冯飞，张洛平，张波. 四自由度机器人Matlab仿真实例[J]. 河南科技大学学报(自然科学版),2008,29(3):24-26.

(责任编辑：王长通)

A 3R1P Manipulator Modeling Design and Experimental Analysis

LI Feng1, YUE Yun2

(1.Collgeg of Information & Business, Zhongyuan University of Technology;2.CATERPILLAR (Zhengzhou) Co., Ltd., Zhengzhou 450007, China)

3R1P manipulator kinematics equation is established by using D-H and kinematics theory, and 3R1P manipulator kinematics model is founded. The simulation model and product are tested，through simulation experiments and manipulator HEBB neural network control experiments, and the system stability is verified. By a detailed analysis of their experimental results the rationality and effectiveness of system modeling and HEBB neural network control have been confirmed. The 3R1P mechanical arm HEBB adaptive neural network diagram of the system is got and the strategy of the smooth run about 3R1P mechanical arm is put forward, and 3R1P mechanical arm development cycles is shortened.

D-H theory; 3R1P manipulator; kinematics equation: HEBB neural network

2015-05-16

河南省教育厅重点科技攻关项目(15A460042)

李峰(1981-)，男，河南南阳人，讲师，硕士，主要研究方向为机器人应用及先进制造技术。

1671-6906(2015)06-0027-06

TH12

A

10.3969/j.issn.1671-6906.2015.06.006