基于软判决加权WHT算法的RSC码盲识别方法*

彭贻云，张　玉，杨晓静

(电子工程学院，安徽 合肥 230037)



基于软判决加权WHT算法的RSC码盲识别方法*

彭贻云，张玉，杨晓静

(电子工程学院，安徽 合肥 230037)

摘要：目前在对Turbo码编码时广泛应用的是递归系统卷积编码器，要完成对Turbo码的识别，首先要对产生的RSC编码参数进行获取。针对低信噪比条件下(n,1,m)RSC码的识别问题，提出运用一种软判决加权Walsh-Hadamard变换(WHT)的方法完成对RSC码的生成多项式的估计。仿真结果表明，在信噪比低于3.5 dB条件下，软判决加权WHT算法比传统的WHT算法具有更好的识别概率。

关键词：信道编码；RSC码；软判决；加权WHT

0引言

随着数字通信技术的发展，信道编码的识别研究也越来越重要。RSC码是Turbo码编码中的主要部分，完成对RSC码的识别是Turbo码识别的基础。

目前，对于卷积码的识别方法主要有快速双合冲算法、欧几里得算法、构建分析矩阵法和Walsh-Hadamard变换法[1]。其中，快速双合冲算法使用较小数据量便能达到识别效果，但只适用于1/2码率卷积码；欧几里得算法[2]改进后可适用于1/n码率，使用的数据量也小，但不具有容错性；构造分析矩阵法可以利用较少数据对(n,k,m)卷积码的参数进行盲识别，但随着误码率变大，容错性极具变化；Walsh-Hadamard变换法只适用于1/n码率卷积码[3]，具有较好的容错性能，但需要获得一定的先验条件，即卷积码的码率和码字起点需要先进行识别。以上方法都只针对一般情况卷积码进行分析，对于RSC码的识别问题没有提出明确的方法，而且主要利用解调硬判决信息进行识别，识别容错性有待提升。本文针对(n,1,m)RSC码的盲识别问题，对文献[1]提出的传统WHT方法进行改进。利用接收到的码字序列，在得到RSC码的编码参数的前提下，通过软判决加权WHT对RSC码的生成多项式进行识别，充分利用解调软判决信息，并能够根据环境设定加权系数，提高识别的容错性。

1问题描述

卷积码是将信源输出信息序列以k个码元分为一段，通过编码器输出长为n(n>k)的一段码字。卷积码与分组码最大的区别是，编码时输出的码字不仅与本组输入信息有关，还有前面若干组输入有关。对于一般情况下卷积码的参数可表示为：(n,k,m),其中k为信息位长度，n为码字长度，m为编码记忆长度。

假设u和c 分别为(n,k,m)卷积码的信息序列和码字序列，在环F2(x)上满足下列关系：

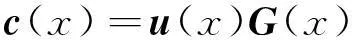
(1)

式中，G(x)为卷积码的生成多项式矩阵。设卷积码的校验矩阵为H(x)，则

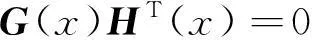
(2)

式中，G(x)为k×n阶多项式矩阵，H(x)为(n-k)×n阶多项式矩阵。由(1)和(2)式可以得到：

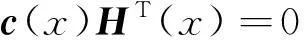
(3)

RSC码的码率一般为1/n，是对(n,1,m)非系统卷积码的改造。对于(n,1,m)RSC码，其生成多项式可表示为：

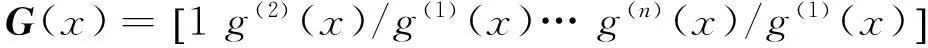
(4)

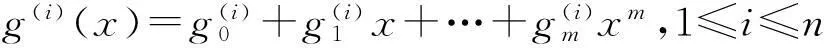
对应的检验矩阵表示为

(5)

式中，右边为一个(n-1)×(n-1)维单位矩阵。

由式(1)和(4)可以得到:

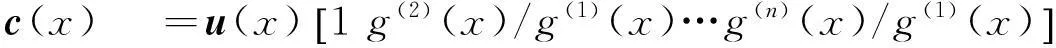
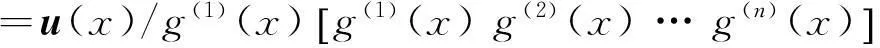
(6)

由(6)式可以看出，RSC码和生成多项式为G′(x)=(g(1)(x)g(2)(x) …g(n)(x))的非递归系统卷积码具有相同的码字集，为便于进行方程的求解，先研究其对应的非递归系统卷积码，再对求出的生成多项式系统化可得到RSC码的生产多项式。对于式(5)中的校验矩阵，同样可以进行化简，得到:

(7)

由式(3)、(6)、(7)得到：

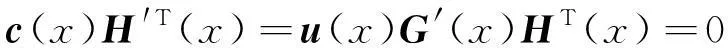
(8)

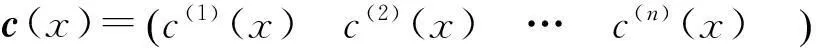
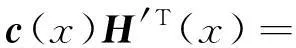
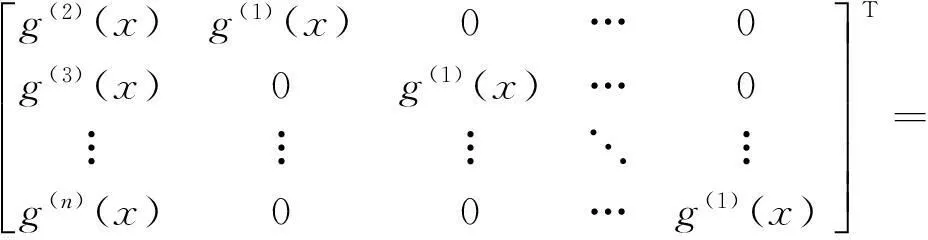
(9)

根据接收到的码字多项式，通过式(9)可以求解方程组得到g(i)(x)(1≤i≤n)，代入式(4)即可得到RSC码的生成矩阵G(x)，完成RSC码的识别。

2模型建立

根据接收到的码字序列按照一定规格构造如下编码矩阵C：

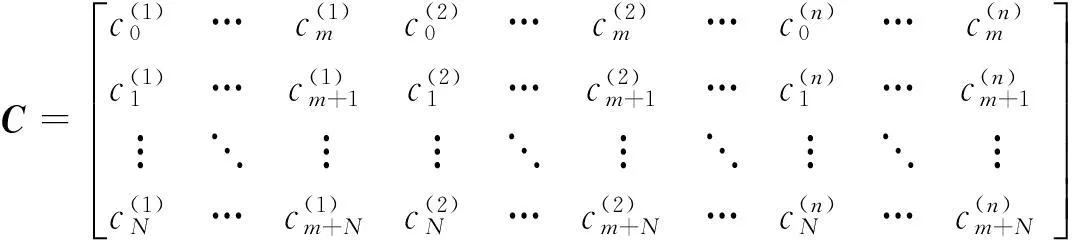
(10)

对式(9)中的第一个方程，从编码矩阵C中抽取数值，构造如下方程，用WHT的方法对方程进行求解。

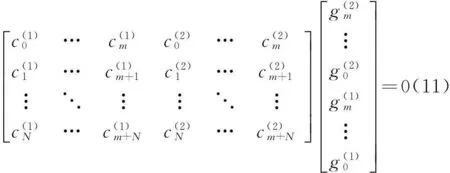
对式(11)求解得到g(1)(x)和g(2)(x)，继续代入式(9)后面的方程，构造如下方程组，利用WHT对方程组求解，依次得到g(3)(x),…,g(n)(x)。

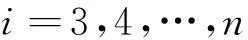
(12)

再将求得的值代入式(4)即可得到RSC码的生成多项式，从而完成对RSC码的识别。至此，将RSC码生成多项式识别转化为对有限域内线性方程组的求解问题。对于方程组的求解，目前性能比较好的主要是利用WHT，本文对该方法进行改进，通过软判决加权WHT的方法实现对性能的提升。

3算法实现

3.1　传统WHT

实际应用中，编码序列往往会受到噪声的干扰导致出现误码的情况，此时对于式(11)就变成一个含错线性方程组的求解：

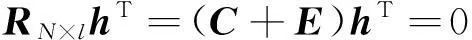
(13)

式中，R表示接收到的码字序列构成的矩阵，E为接收序列的错误图样，h为基本校验矩阵。

以矩阵R中的行向量为地址的单元进行累加，得到频次序列f=(f0,f1,…,f2l-1),fi∈N。然后对f=(f0,f1,…,f2l-1)做WHT：

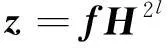
(14)

式中，z=(z0,z1,…,z2l-1)为f的Walsh谱，元素zi是以其地址为解代入方程得到的方程成立个数与不成立个数的差值，H2l为一个2l阶的Hadamard矩阵。向量z中最大项zq的地址就是含错方程(13)的解，它表示最可能满足方程条件的解。

3.2　软判决频次序列

传统WHT识别算法利用接收解调硬判决序列来识别，仅仅只考虑了整个误码率，没有利用各个比特的可靠度信息，在低信噪比条件下，解调输出的序列误码率较高，识别上存在局限。本文引入软判决[4]的序列的方法，将整个方程组成立的概率作为解向量符号度的量度，增加了对接收信息的利用。

软判决解调是指在信号解调过程中，利用每个比特的对数似然比信息(LLR)，判决出输出的信号。在3.1节提到的识别方法中，接收到的编码数据需要转化为接收频次序列后再进一步处理。因此，本文利用接收到的软判决信息，将编码矩阵行向量的可靠度信息作为软判决频次得到接收数据的频次序列，作为后续计算的基础。

假设比特序列在高斯白噪声信道中进行传输，噪声方差为σ2，并且采用的是BPSK调制，此时信噪比SNR=10lg(2/σ2)。当发送比特ci进入信道传输后，得到ri，则此时比特的对数似然比信息(LLR)为：

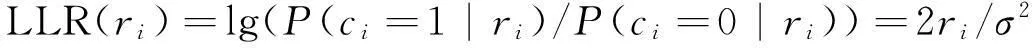
(15)

取LLR(ri)的绝对值作为输出比特ri的可靠度信息,即L(ri)=|LLR(yi)|。将单个比特的可靠度信息推广到整个编码接收序列上，对于构造的接收编码矩阵R，其行向量Ri的可靠度信息为：

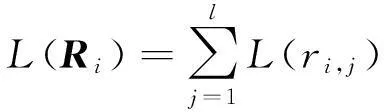
(16)

由于误码在整个序列中占据的只是一小部分，当运用LLR作为比特可靠度信息时，正确码字的可靠度信息将远远高于错误码字的可靠度信息，导致错误码字的影响将会忽略，不利于后续WHT的求解。针对这个问题，引入模糊隶属函数对比特可靠度信息进行缩小范围，更有助于各个码字可靠度的均衡。

对于模糊隶属函数的选取，考虑到比特可靠度信息的分布情况，设置隶属函数为：

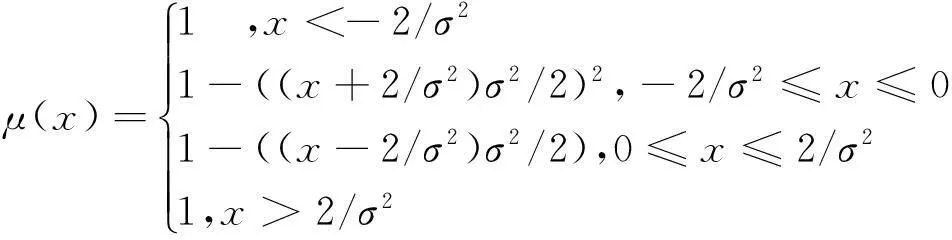
(17)

由此可以得到改进后的比特可靠度K(ri)=μ(LLR(ri))，对应接收编码矩阵行向量Ri的可靠度为：

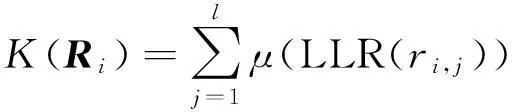
(18)

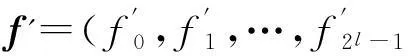
3.3　加权Walsh-Hadamard矩阵

对于WHT得到的Walsh谱z=(z0,z1,…,z2l-1)，则对于其中任意两元素zi、zj，若有zi>zj，则有二进制向量ibin满足的方程数比jbin多，其中解向量的汉明重量即为对接收编码矩阵的行向量作线性计算的抽头数。由式(13)可以看到，由于接收到的码字矩阵存在误码，在不同抽头数条件下，方程错误率不同，当抽头数较多时，方程错误概率也越大。

假设编码序列误码率为p，d为抽头数，对于式(13)的含错方程组，当N足够大时，方程错误个数满足正态分布。在显著水平α的条件下，方程的错误率Pw,i为[5]：

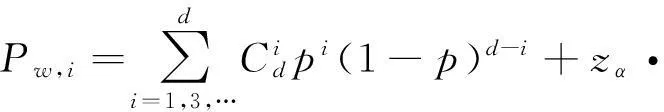
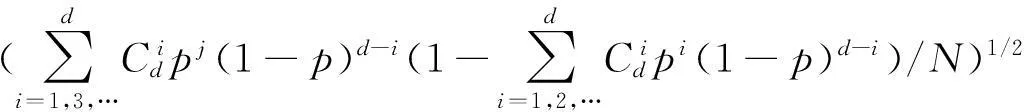
(19)

式中，Φ(zα)=α。

由于不同抽头数导致方程错误概率不同，这里采用Walsh-Hadamard矩阵附加权值的方法，对抽头数较大的向量地址对应的矩阵列向量进行补偿。根据文献中提到的加权条件，在理想情况下，为保证少抽头数和多抽头数条件下算法估计的一致性，Walsh-Hadamard矩阵加权系数如下：

(20)

式中，k为Walsh-Hadamard矩阵的列数。

对Walsh-Hadamard矩阵进行加权重构，得到：

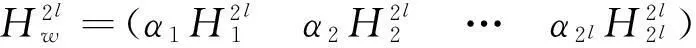
(21)

3.4　RSC码生成多项式识别

在本文求解方程组(11)(12)过程中，主要利用的是提出的软判决加权WHT算法，根据上文的内容，得到对RSC码生成多项式识别的步骤：

1) 利用接收构造的码字矩阵，对于方程组(11)先进行求解。求解采用本文提出的软判决加权WHT算法，先对求出系数矩阵的软次频序列进行加权WHT变换，得到其 Walsh谱，根据谱值大小得到方程组的解。此时，即完成对g(1)(x)，g(2)(x)的求解。

2) 仿照1)中的步骤，依次对方程组(12)进行求解，得出g(3)(x),…,g(n)(x)。

3) 将求出的值代入式(4)，得到RSC码的生成矩阵，完成RSC码的识别。

4仿真及性能分析

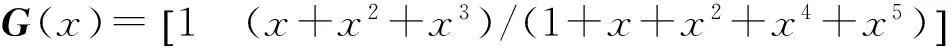
根据上文的限定条件，假设信息序列在AWGN下传输，采用BPSK调制方式，信噪比设定为2dB，利用本文的软判决加权WHT算法和接收到的信息序列对方程(11)求解进行仿真识别，选取方程个数N=600，得到的结果如图1所示。

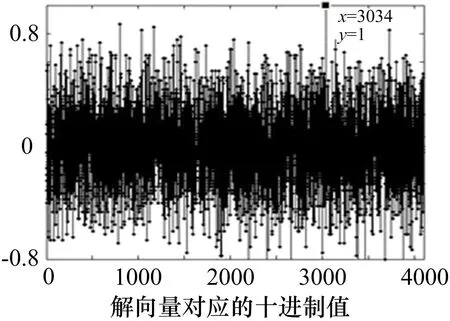
图1　软判决加权WHT识别结果

由图1得到方程组的最优解为3034 其对应二进制数为101111011010，将系数抽取得到接收码字的生成多项式G′(x)=[1+x+x2+x4+x5x+x2+x3]，即RSC码生成多项式为G(x)=[1(x+x2+x3)/(1+x+x2+x4+x5)]，完成对RSC码的识别。

将本文的软判决加权WHT算法与文献[6]中提到的传统WHT算法进行对比，得到两个算法的对比图如图2所示。

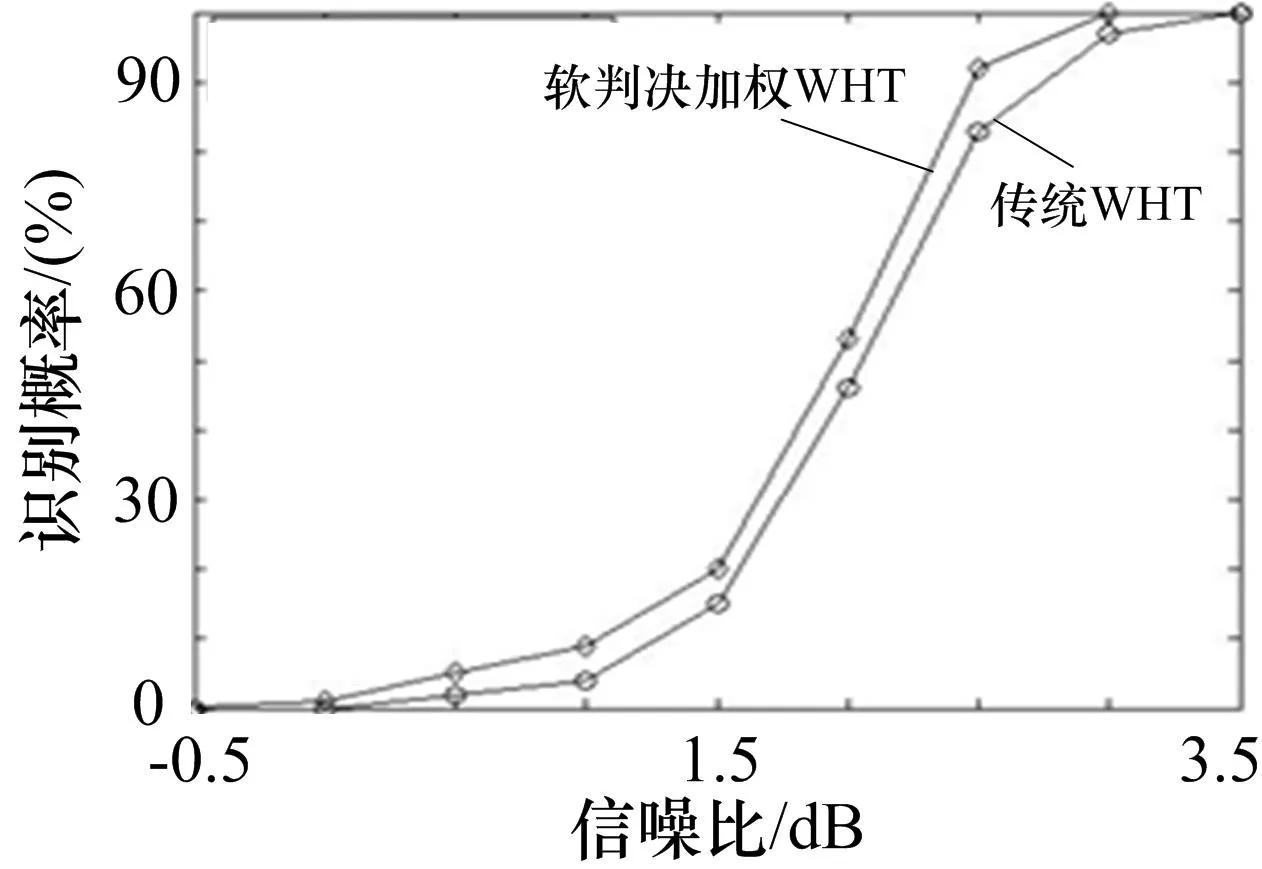
图2　软判决加权WHT与传统WHT识别概率对比

5结束语

本文针对RSC码的识别问题，运用一种软判决加权WHT的算法实现了对RSC码生成多项式的估计。利用接收比特的可靠度信息，对接收矩阵进行重构，再设置加权系数对Hadamard矩阵进行加权处理，对方程组求解进行优化，最后通过重构的接收矩阵和加权Hadamard矩阵得到软频次序列，得到方程组的最优解。与传统的WHT算法进行对比，可见在信噪比小于3.5 dB时，本文算法识别概率得到进一步提升，对于Turbo进一步识别具有较重要的意义。■

参考文献：

[1]解辉，黄知涛，王丰华.信道编码盲识别计算研究进展[J].电子学报，2013,41(6):1166-1176.

[2]刘健成，杨晓静.(n,1,m)RSC码的盲识别[J].电路与系统学报,2012,17(6):84-88.

[3]刘健,王晓君,周希元.基于Walsh-Hadamard变换的卷积码盲识别[J].电子与信息学报,2010,32(4):884-888.

[4]于沛东,李静,彭华.一种利用软判决的信道编码识别新算法[J].电子学报,2013,41(4):301-306.

[5]黄开枝,陈松.基于加权WHT的软判决序列快速估计算法[J].电子与信息学报,2013,35(1):74-79.

[6]张立民，刘杰，钟兆根.(n,1,m)递归系统卷积码的盲识别[J].电讯技术,2014,54(9):1220-1225.

A method for recognizing recursive system convolutional code

based on soft-decision weighted WHT

Peng Yiyun, Zhang Yu, Yang Xiaojing

(Electronic Engineering Institute, Hefei 230037,Anhui,China)

Abstract:Recursive system recursive convolutional code is widely used in the Turbo code coding.First of all,when we want to recognize the Turbo code,we should gain the parameter of RSC code.For the recognition problem of (n,1,m) RSC code in the low signal-to-noise ratio environment,a method based on soft-decision weighted WHT is proposed.It can be used to complete the estimate of RSC code generated polynomial. The simulation results from Matlab show that the algorithm of soft-decision weighted WHT has better recognition probability than algorithm of traditional WHT under the condition of the signal-to-noise ratio is lower than 3.5 dB.

Key words:channel coding; recursive system convolutional code; soft-decision; weighted WHT

中图分类号：TP309

文献标识码：A

作者简介：彭贻云(1992-)，男，硕士研究生，研究方向为信道编码识别研究。

收稿日期：2015-07-01；2015-09-25修回。

*基金项目：国家自然科学基金(61201379)；安徽省自然科学基金(1208085QF103)。