等面积约束的多种干涉仪阵型性能比较分析

刘云龙，郭福成，张　敏，刘　洋

(国防科技大学电子科学与工程学院，湖南 长沙 410073)



等面积约束的多种干涉仪阵型性能比较分析

刘云龙，郭福成，张敏，刘洋

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

摘要：在布阵平面面积一定的条件下，找到使得二维干涉仪测向精度高、解模糊概率大的几何布阵方案是很有意义的。通过理论分析得出8种不同的二维干涉仪阵型测向的CRLB，并通过计算机仿真方式分析了9元阵不同阵型的解模糊概率和各阵型不同阵元个数的解模糊概率，得出了在干涉仪面积一定条件下奇数个数阵元的圆阵是较优的布阵方式的结论。

关键词：测向；解模糊；干涉仪；构型

0引言

估计辐射源来波方向(AOA)，又称之为测向(DF)，在无线电探测、侦察、监视、预警等领域具有重要应用价值[1-3]。干涉仪以其精度高、实时性好、结构简单等特点，被广泛应用于测向系统中。基线越长，测向精度越高。但当基线长度大于半波长时，相位差会出现2π模糊。运用多个阵元的几何关系解相位差模糊实现测向，是工程中常用的测向方法。因此，在干涉仪布阵面积一定的条件下，找到测向精度高、解模糊概率大的基线布阵方式有很大的工程应用价值。

针对阵列布阵几何构型问题，文献[4]提出并分析了圆阵、十字阵、三角阵等二维均匀线阵的测向精度，但是并没有分析二维阵型的解模糊概率问题，也没有分析非均匀二维阵型的测向精度问题。本文通过干涉仪相位差模型计算了多种二维阵型的理论测向克拉美-罗下限(CRLB)。在此基础上，通过文献[5]测向方法，进行了仿真分析，以9元阵为例得到圆阵等各二维阵型的解模糊概率和各阵型不同阵元个数的解模糊概率，得出了奇数个阵元个数的圆阵是较优的布阵方式的结论。

1数学模型

记来波方向与X轴正方向的夹角为方位角(α∈[-π,π])，其中绕逆时针旋转为正角度。来波方向与XOY平面的夹角为俯仰角(β∈[0,π/2])，干涉仪面积为D×D。如图1所示，圆阵为均匀圆阵，相邻阵元与坐标原点的角度相等；十字阵与L阵布阵原则为最小冗余布阵，每维比例为0∶1∶3∶5∶9；矩形阵为均匀阵，环阵的9个阵元坐标分别为(0.5D,0)、(-0.5D,0)、(0,D)、(0.31D,0.18D)、(0.18D,0.31D)、(-0.31D,0.18D)、(-0.18D,0.31D)、(0,0.6D)、(0,0.8D)；菱形环形阵的9个阵元坐标分别为(0,0)、(0.5D,0.5D)、(0.4D,0)、(-0.5D,0.5D)、(0,0.4D)、(-0.5D,-0.5D)、(-0.4D,0)、(0.5D,-0.5D)、(0,-0.4D)；M阵9个阵元坐标为(0.5D,0)、(0.35D,0.6D)、(0.25D,D)、(0.08D,0.35D)、(0,0)、(-0.15D,0.6D)、(-0.25D,D)、(-0.41D,0.35D)、(-0.5D,0)。

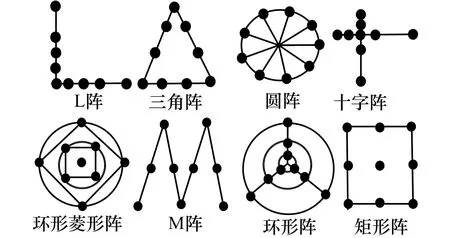
图1　二维阵型布阵示意图

假设目标辐射源波长为λ，天线个数为M，n表示观测次数，天线与坐标系X轴正半轴夹角为θi(i=1,2,…,M)。天线i与坐标原点距离为di，天线初始相位为φ0，由于天线和接收通道相互独立，因此接收信号处理后的相位之间可认为近似独立的：

(1)

式中，δi和δk为天线i和k的相位测量误差，从而服从均值为零、方差为δ的高斯分布。

则天线i的接收通道得到的相位为：

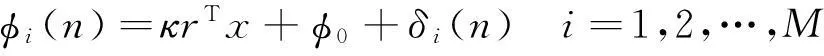
(2)

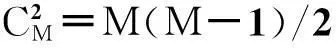
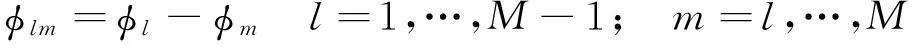
(3)

式中，φlm表示天线l与天线m的相位差。

命题：若二维干涉仪有M个阵元，且每个阵元独立分布，将M个天线两两相减得到的相位差仅有M-1个相位差是独立的，其余相位差皆可由这M-1个相位差线性组合而成。下面将证明这个结论：

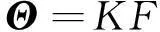
(4)

式中，Θ=(φ12,φ13,…,φM-1M)T；Φ=(φ1,φ2,…,φM)；K矩阵表达式为：

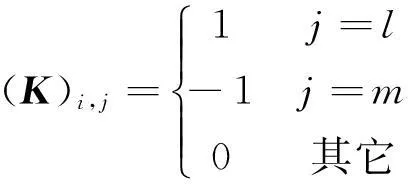
(5)

式中，i为基线编号，j为天线标号，l为第1根天线标号，m为第2根天线标号。

将K矩阵行列式变换得：

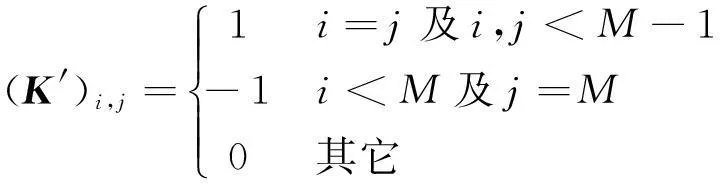
(6)

从式(6)可以得到：

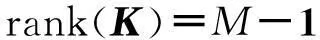
(7)

即矩阵K的极大无关组个数为M-1，可知，由独立初相求得的相位差只有M-1是独立的。从式(6)可以看出，这M-1个独立相位差是由任意一个天线与其它M-1个天线相减得到的相位差，可以将这M-1个相位差记为φlmj。l为任意天线，mj为除l天线外其它天线，j=1,2,…,M-1。

由式(2)可得，天线l与天线mj的相位差φlmj为：

(8)

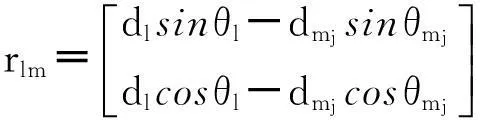
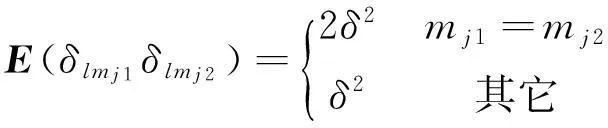
(9)

由式(8)可以得出：

(10)

(11)

式中，Θ=(φlm1,φlm2,…,φlmM-1)T;E=(δlm1,δlm2,…,δlmM-1)T;G(θ)=(glm1(θ),glm2(θ),…,glmM-1(θ))T。

当基线长度大于波长的一半时，测得的相位差可能出现2π模糊。即：

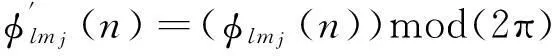
(12)

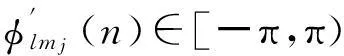
由式(9)可得：

(13)

2解模糊概率分析

下面分析无模糊相位差的测向误差的CRLB下限，将其作为比较二维阵型测向精度的标准。

由Fisher信息矩阵定义，可得：

(14)

式中，p(Θ;θ)为θ的联合概率密度函数。P为相位差关于θ的Jacobi矩阵。

P=HJ

(15)

式中，H=(rlm1,rlm2,…,rlmM-1)T；

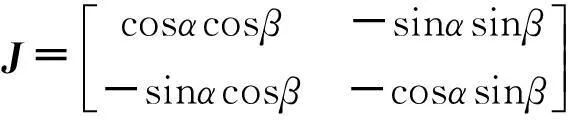
由式(9)的相位差噪声假设对应协方差为W=δ2CN，其中：

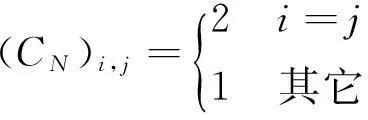
(16)

可得Fisher信息矩阵为：

(17)

其中θ=(α,β)T由CRLB定义可得：

(18)

根据式(18)可以计算得到图1中二维阵型测向精度的理论CRLB结果，如表1所示。

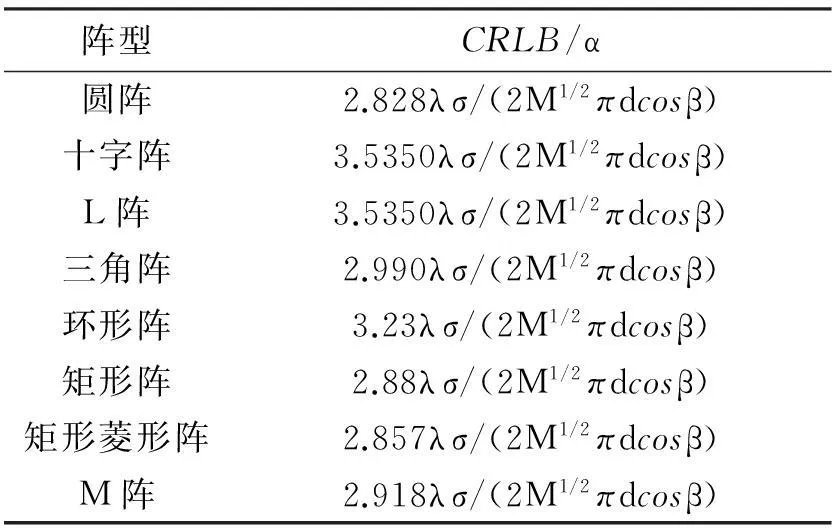
表1　不同阵型的测向误差的CRLB

从表1可以看出，圆阵的CRLB小于其它阵的CRLB，L阵的测向精度与十字阵测向精度相当，阵型的测向精度与阵元个数成反比关系。

3解模糊概率分析

(19)

通过计算机仿真，对二维阵型的解模糊概率进行仿真。为了评估性能，采用MonteCarlo重复试验统计解模糊概率。定义方位角和俯仰角均方根(RMS)误差为：

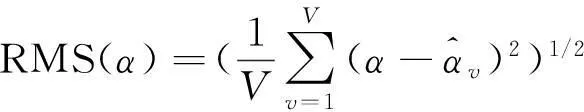
(20)

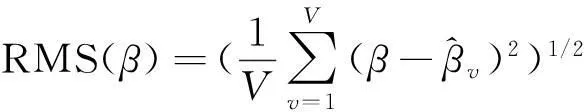
(21)

场景参数：干涉仪最大面积约束为0.6m×0.6m的正方形，信号频率为3GHz。相位差误差为15°，方位角为30°，俯仰角0°～90°，当解模糊概率小于50%时，则认为不能解模糊。

仿真一：不同阵型9元阵解模糊概率，如图2所示。

图2　不同阵型9元阵解模糊概率图

仿真二：各阵型不同阵元个数解模糊概率，如图3所示。

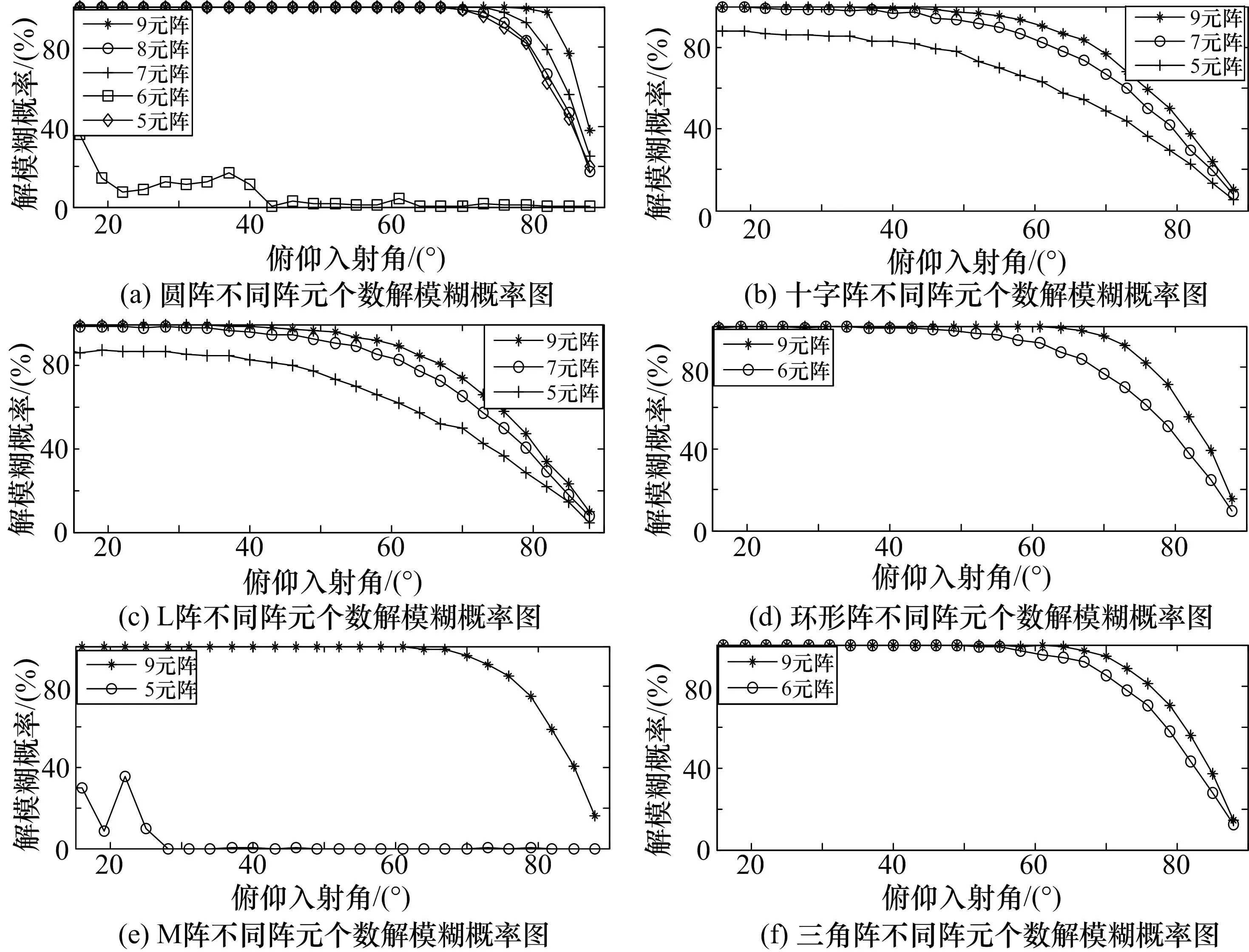
图3　各阵元不同阵元个数解模糊概率仿真图

从以上仿真可以得出：

1)9元阵中，在俯仰角为小角度时，以上阵型的解模糊概率都可以接近100%，但是当俯仰角增大到70°时，圆阵的解模糊概率要优于其它阵型。说明圆阵有更好的角度适应性。

2)圆阵的7元阵的解模糊概率要优于8元阵，6元阵不能解模糊。说明圆阵的奇数阵解模糊概率要优于偶数阵。但是不论奇数阵或者偶数阵，阵元个数越多，解模糊概率越高。

4结束语

本文分析了圆阵等二维阵型的测向精度与解模糊概率，在干涉仪面积一定的条件下，圆阵的测向精度要高于其它阵型。奇数个阵元个数的圆阵的解模糊概率有更好的角度适应性。综上所述，奇数个阵元个数的圆阵是较优的布阵方式。■

参考文献：

[1]YangR,FooPH,NgBP,etal.RFemittergeolocationusingamplitudecomparisonwithauto-calibratedrelativeantennagains[J].IEEETrans.onAerospaceandElectronicSystem, 2011, 47(3): 2098-2110.

[2]MacphieRH,TaeHY.Onusingthecompoundinter-ferometertoobtainthepowerpatternofaconventionalreceivingarray[J].IEEETrans.onAntennasandPropagation, 2009,10(57):3356-3359.

[3]郭福成,樊昀,周一宇,等. 空间电子侦察定位原理[M].北京:国防工业出版社,2012.

[4]YingBH，DonaldD.Weiner.AnL-sharedarrayfor

estimating2-Ddirectionsofwavearrival[J].IEEETrans.onAntennasandPropagation, 1991,39(2):143-146.

[5]张敏，郭福成，李腾，等.旋转长基线干涉仪测向方法及性能分析[J].电子学报,2013,41(12):2422-2429.

A comparative analysis of performances for different shaped phase

interferometers with area constraint

Liu Yunlong, Guo Fucheng, Zhang Min, Liu Yang

(College of Electronic Science and Engineering,National University of Defense

Technology,Changsha 410073,Hunan,China)

Abstract：It is meaningful to find the optimal shape for the phase interferometer to improve the direction finding accuracy and solving ambiguity probability on the condition of certain plane areas and certain element numbers. The Calmer Rao Low Bound (CRLB) of direction finding of eight different shaped 2-D interferometers are given with nine-elements.Simulations are performed to investigate the direction finding accuracy and the solving ambiguity probability of the above different shaped arrays. The theoretical analysis and simulation indicate that circular array with an odd number of elements is the best choice under certain planes areas.

Key words：direction finding;solving ambiguity;interferometer;array

中图分类号：TN971+.5

文献标识码：A

作者简介：刘云龙(1990-)，男，硕士研究生，主要研究方向为无源定位、信号处理。

收稿日期：2015-06-20；2015-09-26修回。