考虑气-液交界面的非饱和土有效应力公式

张 昭，刘奉银，张国平

（1. 西安理工大学 岩土工程研究所，陕西 西安 710048；2. 麻省大学阿姆斯特分校 土木及环境工程系，美国 阿姆斯特 01003）

1 引 言

Terzaghi于1936年的有效应力原理是饱和土力学的理论基础之一，不仅将土骨架内总应力与流体相压力组合，而且描述了土骨架的力学变形特性。随后学者们[1－8]致力于将其推广至非饱和土，其中Bishop于1959年提出了非饱和土有效应力的单变量公式[1]。该公式的优势在于将多相介质通过力学等效转化为单相介质，其中的有效应力参数χ描述了基质吸力对有效应力的贡献。学者们从理论和试验方面对χ的变化规律进行了一系列定量研究。陈正汉等[2]用两种孔隙率的非饱和土的体积模量来表征χ。Loret等[3]和Laloui等[4]认为χ应表示为土孔隙尺寸、孔隙气压力和孔隙水压力的函数。Alonso等[5]从理论上证明了饱和度不能直接表示χ。Khalili等[6]在总结分析了大量控制基质吸力的直剪和三轴剪切试验结果后得出用基质吸力ψ和进气值ψaev表示的χ表达式，并对3种土进行了多阶段减、增湿三轴剪切试验[7]，结果发现干湿循环对χ影响显著（尤其在扫描阶段），并将他们在文献[6]中提出的χ表达式推广至干湿循环阶段。然而，上述研究均未深入讨论干湿循环对有效应力（或有效应力参数χ）的影响机制。实际上，土骨架中气、液、固三相及其交界面（如气-液交界面）的相互作用从微观角度控制着其力学特性，Khalili等[7]也将干湿循环对χ的显著影响归结为气-液交界面的影响，但未考虑这种相间交界面对有效应力的贡献。气-液交界面可将毛细作用力施加在土颗粒上以阻止其在外力作用时滑动[8]，而毛细作用力在非饱和土的有效应力中有显著贡献，因缺乏深入认识而在有效应力公式中常被忽略，而且气-液交界面如何通过毛细作用影响有效应力尚未得到土力学界的证实。此外，要模拟非饱和土的力-水耦合特性，尚需完整认识土骨架内部的应力状态及其对气-液交界面自由能的影响。近年来，Coussy[9]和Pereira等[10]通过在有效应力公式中考虑气-液交界面的自由能以反映其影响，但未考虑相间交界面的守恒方程。值得注意的是，非饱和土可简化为气、液、固三相及其交界面组成的集合体，Houlsby[11]、Zhao等[12]、Fuentes等[13]虽利用热力学原理和多孔介质理论研究了非饱和土的变形功和有效应力的关系，但均未考虑气-液交界面。Hassanizadeh等[14]较早地考虑了气、液、固三相及其交界面，用以模拟非饱和土内气、液两相的流动，但未考虑力-水耦合特性。

为此，遵照Hassanizadeh等[14]的方法，建立气、液、固三相及其交界面的守恒方程和相应的限制条件，求解有效应力公式时采用的守恒方程属普适性方程，力-水耦合特性的特殊性多反映在本构假定中，笔者在Helmholtz自由能中考虑力-水耦合特性，试图推导考虑气-液交界面的非饱和土有效应力公式；根据该公式确定有效应力参数后，利用Khalili等[7]对3种土的多阶段减、增湿三轴剪切试验结果验证有效应力参数表达式比较已有文献表达式在描述干湿循环下有效应力参数与基质吸力关系时的有效性。

2 有效应力公式的推导

2.1 各相及其交界面的守恒方程

对非饱和土中的流体相考虑为液、气两相，分别用l、a表示。固相为土骨架，用s表示。气、液、固三相相互接触且两两形成交界面，即气-液交界面，用la表示；固-液交界面，用ls表示；固-气交界面，用as表示；在3个交界面间存在一条公共线，用las表示，不仅联系各相及其交界面，而且实现各交界面质量、动量、能量和熵的转换。

2.1.1 质量守恒方程

此外，若假定公共线不存在热力学性质，则上述守恒方程中相应的交换项满足如下限制条件：

2.2 在Helmholtz自由能中考虑力-水耦合特性

上述守恒方程不能完整表征各相及其交界面组成的集合体，需补充本构假定。出于推导简便，在本构假定中可采用各相及其交界面的Helmholtz自由能函数替换相应的内能：

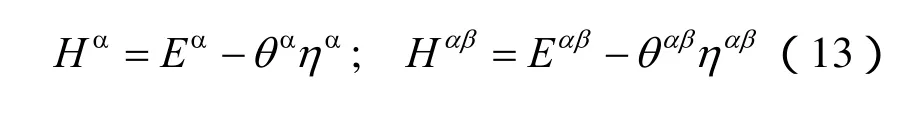
如前所述，力-水耦合特性在本构假定中的反映，笔者通过在各相及其交界面的Helmholtz自由能中考虑力-水耦合特性以实现。土力学中认为土颗粒呈刚性，则此时土颗粒运动引起的土材料孔隙变化会使气-液交界面的曲率发生变化，致使其Helmholtz自由能也发生变化[16]，可忽略对固-液、固-气交界面 Helmholtz自由能的影响。为表征力-水耦合特性，可以假定气-液交界面的Helmholtz自由能与固相的拉格朗日应变张量有关，笔者从土力学角度假定它与土材料的孔隙率ε有关，则此时Helmholtz自由能可表示为关于如下独立变量的函数：

2.3 考虑气-液交界面的有效应力公式

3 有效应力参数的确定

章节2提出的有效应力公式（17）因包含表征气-液交界面影响的lalak AI项而不同于传统的单变量公式，但可将其整理为与类似的形式，以确定有效应力参数χ：

图1 F-75 Ottawa砂内气-液交界面的面积密度 A la 与饱和度 sl的关系Fig.1 Areal density of air-liquid interface Alaversus degree of saturationslin F-75 Ottawa sand

4 有效应力公式的验证

Khalili等[7]对布法罗大坝低塑性黏土（简称BC）、伯克低塑性粉土（简称BS）、悉尼砂（75%）和高岭土（25%）的混和土（简称 SS-KL）3种压实试样（初始干密度ρd0=1.80、1.53、1.63 g/cm3）进行了多阶段减、增湿三轴剪切试验（试验用土的物理力学性质参数见文献[7]）：先对饱和试样进行常规固结排水试验，进而减湿至预设的基质吸力值，再进行控制基质吸力的固结排水试验，如此交替，最后进行控制净应力和轴向应变的增湿试验，在边界减、增湿和扫描阶段测定了不同基质吸力对应的饱和度及有效应力参数。笔者利用该试验结果验证式（20）在表征干湿循环下有效应力参数χ与基质吸力ψ关系时的有效性。

首先，采用 Fredlund等[20]和 Khalili等[21]提出的模型分别对边界减、增湿和扫描阶段的持水实测值（基质吸力与饱和度）进行拟合：

式中：m、n、a、Z、U、Y均为拟合参数；patm为大气压力（101 kPa）。对边界减、增湿阶段的持水实测值拟合时，先确定控制持水曲线残余段位置的参数m[20]，使拟合曲线通过边界减、增湿阶段的最后一个数据点，再利用约束型最小二乘法确定参数a、n，进而利用拉格朗日乘数法使拟合曲线逼近连接边界减、增湿和扫描阶段的基质吸力反向点；对扫描阶段的持水实测值拟合时，先确定参数U，再通过调整参数Y和Z使拟合曲线亦能通过两个基质吸力反向点，以实现该曲线在基质吸力反向点处连续。3种土的持水实测值、式（21）确定的拟合曲线及相应的模型拟合参数如图2所示。从图中可以看出，式（21）适于表征3种土在干湿循环下的持水特性。其次，将边界减、增湿阶段持水模型的拟合曲线代入式（20），使之与相应阶段中不同基质吸力对应的有效应力参数实测值进行拟合确定其中的参数Cmn。最后，将扫描阶段持水模型的拟合曲线代入参数Cmn已知的式（20）中，得到该阶段不同基质吸力对应的有效应力参数χ预测值。

此外， Khalili等[7]也提出了边界和扫描阶段的χ表达式：

图2 3种土在边界减、增湿和扫描阶段的持水实测值[7]及其拟合曲线Fig.2 Curves of measured[7] and fitted boundary drying-wetting and scanning water retention for three soils

图3 3种土在边界减、增湿和扫描阶段的有效应力参数拟合(预测值)值、实测值[7]与基质吸力的关系Fig.3 Measured[7] and fitted (predicted) effective parametersvs. matric suction in boundary drying-wettingand scanning process for three soils

5 结 论

（1）将非饱和土简化为各相及其交界面组成的集合体，假定气-液交界面的Helmholtz自由能与土材料的孔隙率有关。将各相及其相间交界面的守恒方程及Helmholtz自由能函数的物质导数联立代入熵不等式，根据该不等式适用于所有热力学状态推得考虑气-液交界面面积密度的非饱和土有效应力公式。

（2）将气-液交界面的面积密度表示为基质吸力与饱和度的函数，得到有效应力参数的表达式。最后，利用已有文献中3种土的多阶段减、增湿三轴剪切试验结果，对比分析了有效应力参数表达式与已有文献表达式在表征干湿循环下有效应力参数与基质吸力关系时的有效性。结果发现，该表达式对边界减、增湿及扫描阶段有效应参数的拟合（预测）效果优于已有文献表达式，故可证明饱和度变化很小时有效应力参数的显著变化是由气-液交界面变化产生的，有必要在有效应力公式中引入气-液交界面。

[1] BISHOP A W, BLIGHT G E. Some aspects of effective stress in saturated and partly saturated soils[J].Geotechnique, 1963, 13(3): 177－197.

[2] 陈正汉, 王永胜, 谢定义. 非饱和土的有效应力探讨[J].岩土工程学报, 1994, 16(3): 62－69.CHEN Zheng-han, WANG Yong-sheng, XIE Ding-yi.Effective stress in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 62－69.

[3] LORET B, KHALILI N. An effective stress elastic-plastic model for unsaturated porous media[J]. Mechanics of Materials, 2002, 34(2): 97－116.

[4] LALOUI L, KLUBERTANZ G, VULLIET L. Solidliquid-air coupling in multiphase porous media[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(3): 183－206.

[5] ALONSO E E, PEREIRA J M, VAUNAT J, et al. A microstructurally based effective stress for unsaturated soils[J]. Geotechnique, 2010, 60(12): 913－925.

[6] KHALILI N, GEISER F, BLIGHT G E. Effective stress in unsaturated soils: Review with new evidence[J].International Journal of Geomechanics, 2004, 4(2):115－126.

[7] KHALILI N, ZARGARBASHI S. In fl uence of hydraulic hysteresis on effective stress in unsaturated soils[J].Geotechnique, 2010, 60(9): 729－734.

[8] MATYAS E L, RADHAKRISHNA H S. Volume change characteristics of partially saturated soils[J].Geotechnique, 1968, 18(2): 432－448.

[9] COUSSY O. Revisiting the constitutive equations of unsaturated porous solids using Lagrangian saturation concept[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(15):1675－1694.

[10] PEREIRA J M, WONG H, DUBUJET P. Adaptation of existing behaviour models to unsaturated states:application to CJS model[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2005, 29(11): 1127－1155.

[11] HOULSBY G T. Work input to an unsaturated granular material[J]. Geotechnique, 1997, 47(1): 193－196.

[12] ZHAO C G, LIU Y, GAO F P. Work and energy equations and the principle of generalised effective stress for unsaturated soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2010, 34(9): 920－936.

[13] FUENTES W, TIANTAFYLLIDIS TH. On the effective stress for unsaturated soils with residual water[J].Geotechnique, 2013, 63(16): 1451－1455.

[14] HASSANIZADEH S M, GRAY W G. Mechanics and thermodynamics of multiphase fl ow in porous media including interphase boundaries[J]. Advances in Water Resources, 1990, 13(4): 169－186.

[15] SPAEPEN F. Interfaces and stresses in thin fi lm[J]. Acta Materialia, 2000, 48(1): 31－42.

[16] CHHAPADIA P, MOHAMMADI P, SHARMA P.Curvature-dependent surface energy and implications for nanostructures[J]. Journal of the Mechanics and Physics of Solids, 2011, 59(10): 2103－2115.

[17] LU N, ZEIDMAN B D, LUSK M T, et al. A monte carlo paradigm for capillarity in porous media[J]. Geophysical Research Letters, 2010, 37(23): 1－5.

[18] WILLSON, C S, LU N, LIKOS W J. Quantification of grain, pore, and fluid microstructure of unsaturated sand from X-ray computed tomography images[J]. Geotechnical Testing Journal, 2012, 35(6): 911－923.

[19] JOEKAR-NIASAR V, HASSANIZADEH S M, LEIJNSE A. Insights into the relationships among capillary pressure,saturation, interfacial area and relative permeability using pore-network modeling[J]. Transport in Porous Media,2008, 74(2): 201－219.

[20] FREDLUND D G, XING A. Equation for the soil-water characteristic curve[J]. Canadian Geotechnical Journal,1994, 31(4): 521－532.

[21] KHALILI N, HABTE M A, ZARGARBASHI S. A fully coupled fl ow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses[J]. Computers and Geotechnics, 2008, 35(6):872－889.