海上风机分段斜壁桶形基础的水平承载力计算方法

刘金龙，陈陆望，王吉利，汪东林

（1.合肥学院 建筑工程系，安徽 合肥 230601；2.合肥工业大学 资源与环境工程学院，安徽 合肥 230009；3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点试验室，湖北 武汉 430071；4.安徽建筑大学 土木工程学院，安徽 合肥 230601）

1 引 言

据测算，我国近海 10 m水深的风能资源约 1亿kW，近海20 m水深的风能资源约3亿kW以及近海30 m水深的风能资源约4.9亿kW，是陆地风能资源的2倍，具有巨大的风能开发潜力[1-2]。海上风电具有风速高、损耗低、产出高、环境污染小、不占用耕地等优点，近年来已成为各国竞相研究和开发的热点[3]。

然而海洋环境较为恶劣，地质条件极端复杂，存在厚度及覆盖范围较大的软土、可液化砂质土等不良地基，这大大增加了海上风电工程建设的难度与投资风险。可见，海上风电工程的基础设计极具挑战性。

目前海上风机多数采用重力混凝土和钢桩结构基础[4-5]。如2003年建成投产的丹麦Samso近海风电场采用了单立柱钢质单桩结构，桩径为4.5 m，为当时直径最大的桩[6]。我国第一座大型海上风电场——东海大桥海上风电工程（如图1所示）采用钢结构和混凝土互混的结构：先打下8根钢管桩，再在钢管桩顶部浇注成一个混凝土承台，以满足风机的承载、抗拔、水平移位等需要。但桩基础的施工对打桩要求比较高，施工过程对海床产生一定的扰动，费用也较高。特别在部分浅海不具备打桩的施工环境（大型施工船舶无法进入），传统的风电基础形式不再适用，需发展一种更加高效与经济的新型风电基础形式。

桶形基础就是为适应海洋地质条件而发展起来的一种基础形式，其上部封闭、底部开口，因像倒扣在土中的圆桶而得名，可用于海上风电工程、浅海石油与天然气资源开发、海上浮动式结构物的系泊工程等[7]，被称为导管架基础工程技术新时代的曙光。

目前研究与使用的桶形基础多为直壁圆桶形式[8-12]。如Europipe 16/11-E的导管架由4个直径12 m、桶高9.5 m的桶形基础承担[13]，平台总重量为5 240 t；渤海湾西南部海洋石油QHD32-6-4中的吸力锚为桶直径为6.0 m、桶高为3.2 m、单个锚重为 35 t的桶形基础；中国南海西部海域的文昌13-1、文昌13-2油田中，用于浮式生产存储、卸油系统系泊的吸力锚直径为5.0 m、高度为11.5 m，单个锚重为50 t[14]。

事实上，为了把应力扩散到更大面积的桶底土层上，可以采用斜壁形式的桶形基础[15-16]。目前对这种新型的桶形基础研究较少，缺乏有效的试验数据，对其承载力与稳定性的计算更无规范可参考。

考虑到施工的科学性与可行性，现进一步提出一种新型斜壁桶形基础——分段斜壁桶形基础。为此，本文基于力学分析方法，对分段斜壁桶形基础的水平承载力进行了系统性研究，考察了斜壁倾角、桶高、桶径、土性参数等对水平承载力的影响，为分段斜壁桶形基础的设计与应用提供参考。

2 水平承载力计算方法

2.1 计算模型

当分段斜壁桶形基础达到水平极限平衡状态时，其受力模型如图2所示。图中，H为桶体高度（m）；D为桶顶部直径（m）；β1为上部斜壁倾角（°）；β2为下部斜壁倾角（°）；Pu为水平极限荷载（kN）；Lp为水平荷载的作用高度（m）；σx为作用于外侧桶壁的水平土体抗力（kPa）；σx0为最大水平土体抗力（kPa）；σr为作用于外侧桶壁的径向土体抗力（kPa）；σz为作用于桶底的竖向土体抗力（kPa）；T1为作用于前侧外桶壁的摩擦合力（kN）；T2为作用于后侧外桶壁的摩擦合力（kN）；Tb为作用于桶底的摩擦力合力（kN）。桶形基础在水平极限荷载作用下绕A点旋转而发生失稳（失效）。

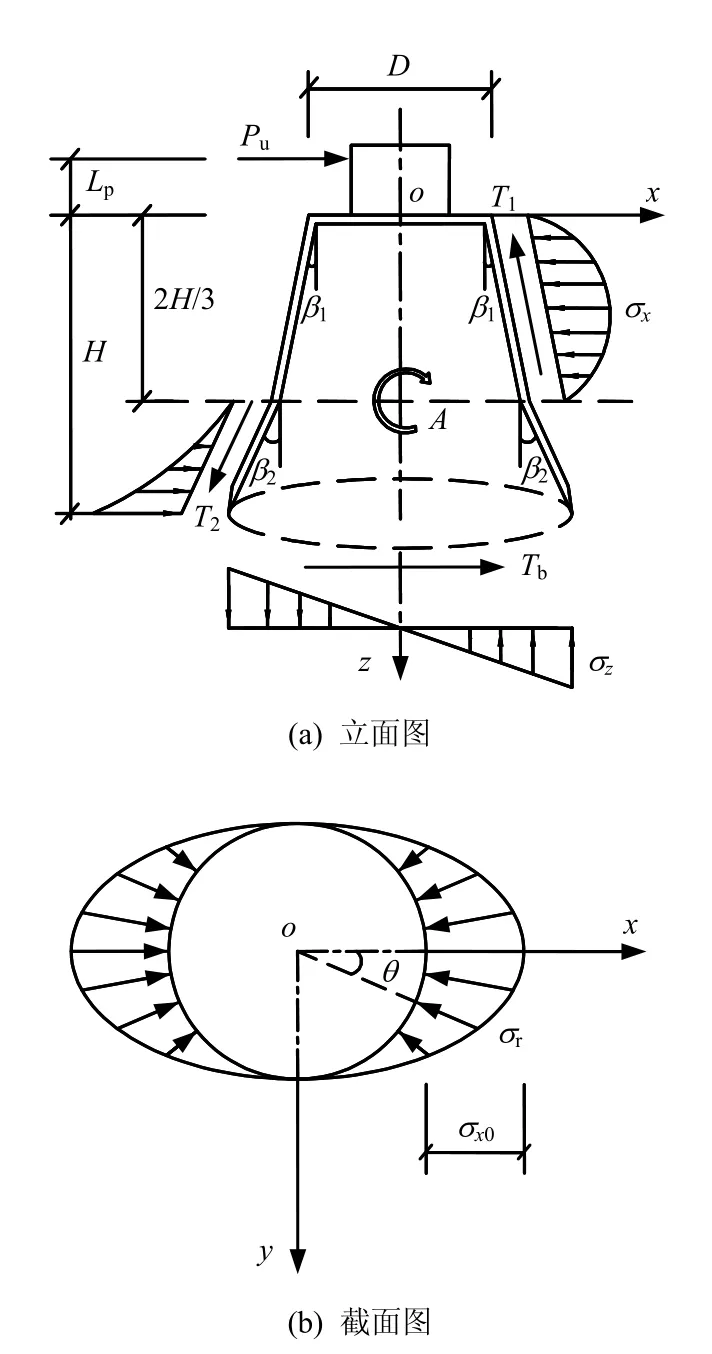
图2 分段斜壁桶形基础受力分析模型Fig.2 Analytic model of segmentally-tapered bucket foundation

2.2 基本假定

（1）笔者的前期研究结果表明，桶壁倾角对旋转点A的位置影响较小。A点位于距桶顶大约2H/3处，桶壁倾角的变化对A位置的影响程度较小（下文将进一步分析其影响程度）。故现假定旋转点A的位置为2H/3处（如图2(a)所示），为使力学分析过程更为简化。以旋转点A为界，桶壁上方2H/3范围向外倾斜β1，桶壁下方H/3范围向外倾斜β2，此即为本文所提出的分段斜壁桶形基础形式。

（2）桶基内部被土体填充密实无空隙，桶基与其内部的土塞视为一个统一刚性体，即内部土塞与桶内壁之间不再发生变形与变位。

（3）作用于外侧桶壁上的水平土体抗力服从Winkler假定，在xoz平面内水平抗力沿桶高呈抛物线分布，如图2(a)所示，其表达式为

式中：kx为水平向地基系数，可由m法确定，即kx=mz，其中m为比例常数，由试验确定；ω为桶基在水平荷载作用下产生的转角。

桶基在水平荷载作用下绕A点发生失效即倾覆破坏。故本文所指的桶基水平承载力即指桶基发生倾覆破坏时的水平抗力。

（4）在xoy平面内，土体径向水平抗力沿桶周呈三角函数关系分布，如图2(b)所示，其表达式为

（5）作用于外侧桶壁上的土体摩擦力τz与该处的径向水平土体压力σr成正比，即

式中：f为土体与桶壁之间的摩擦系数，由试验确定。

（6）作用于基底表面上的竖向土体抗力也服从Winkler假定，如图2(a)所示，其表达式为

式中：kz为竖向地基系数，可取kz≈ 2kx[17]。

2.3 受力分析

桶基前侧水平土压力合力N1（积分示意图见图3）为

图3 斜壁桶基侧壁积分示意图Fig.3 Integration on wall of tapered bucket

桶基前侧水平土压力合力N1对转动中心A点产生的弯矩M1为

由x方向力平衡、z方向力平衡、绕A点的弯矩平衡推导得到：

可见，式（13）即为本文所提分段斜壁桶形基础的水平承载力计算公式。需说明的是，鉴于倾角数值较小，在数学求解过程中对x方向、z方向的力平衡采取了近似简化处理（下文将论证这种简化做法的合理性）。

2.4 几种特殊情况

图2所示的分段斜壁桶形基础的倾角β1、β2取值是任意的，当β1、β2取值比较特殊时，可形成多种特殊的桶基构型，如图4所示。

根据式（13）便可得到，图4所示特殊结构形式的水平承载力计算方法。

（1）当β1=β2= 0 °时，变为传统的直壁桶形基础（见图4(a)），其水平承载力计算公式为

而式（14）与文献[17]所给的计算公式相同。因此，文献[17]所提的直壁桶形基础水平承载力计算公式，可看作是本文分段斜壁桶基水平承载力式（13）在β1=β2= 0 °情况下的一个特例。

图4 分段斜壁桶形基础的特例Fig.4 Special cases of segmentally-tapered bucket foundation

（2）当β1=β2=β≠ 0 °时，变为整个桶壁倾斜角度相同的桶形基础（见图4(b)），其水平承载力计算公式为

（3）当β1=0°、β2≠0°时，变为上部桶壁直立、下部桶壁倾斜的桶形基础（见图4(c)），其水平承载力计算公式为

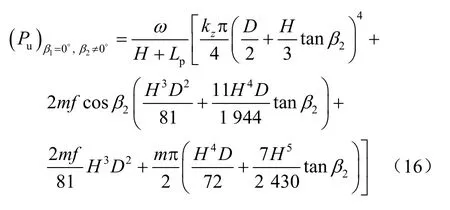
（4）当β1≠0°、β2=0°时，变为上部桶壁倾斜、下部桶壁直立的桶形基础（见图4(d)），其水平承载力计算公式为

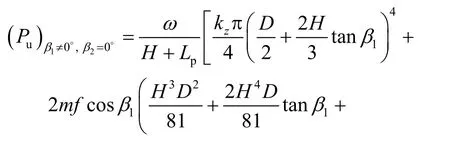
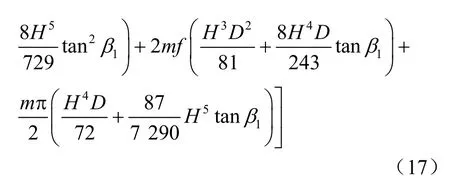
3 计算结果与模型试验的比较

关于桶形基础的模型试验较少，而关于斜壁桶形基础的试验研究更鲜有文献提及。文献[18]给出了一种直壁桶形基础的模型试验方案与实测结果，其参数为D= 0 .5 m ，Lp= 0 .1 m ，ω= 0 .02 rad，f=0.327 8。地基反力比例系数m需根据试验确定（原文献未提供），参考桩基规范流塑状黏性土m=6～14 M N/m4，此处取m= 8 000 kN/m4。

单桶基础水平承载力Pu试验结果与计算结果的比较见表1。

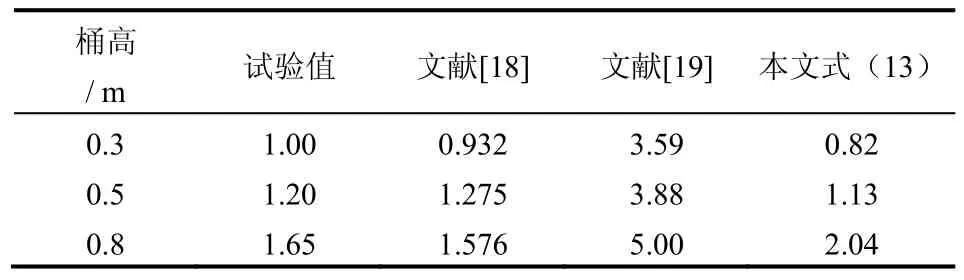
表1 水平承载力计算结果与试验结果的比较(单位: kN)Table 1 Comparison between theoretical results and model test value of horizontal bearing capacity of foundation (unit: kN)

由表 1数据可见，文献[18]与本文计算结果与实测值更为接近，而文献[19]的误差较大。进一步比较可知，文献[18]所提计算公式中所考虑的影响因素较多，导致其表达式是隐式方程，需进行复杂迭代计算才能求得桶形基础的水平承载力，不便于在实际工程中的应用。而本文所提计算方法式（13）为显函数，只要代入桶形基础的基本参数，很快即可得到水平承载力的计算值。

需要指出的是，以上公式仅在较小尺度的室内模型试验中进行了验证，是计算斜壁桶形基础水平承载力的一种尝试。倘要应用于工程实际，还需进一步开展大尺度（如1:1模型）的模型试验研究，有待进一步验证与修正。

4 参数敏感性分析

通过上述力学分析得到了分段斜壁桶形基础的水平承载力计算方法式（13），其含有较多的计算参数，有必要进一步探讨各计算参数对水平承载力的影响，即参数敏感性分析。

现以几内亚湾内Nkossa油气田的吸力锚（距刚果PoinLe Noire 西南60 km处）为分析对象进行参数敏感性分析，其参数为D=4 m，H= 1 2 m ，海域水深即Lp=175 m ，ω= 0 .02 rad ，f=0.327 8，m= 8 000 kN/m4。参数敏感性分析时，仅变换要考察的参数，其余参数取值不变。

4.1 桶壁倾角β1、β2对水平承载力Pu的影响

桶壁倾角β1、β2的不同取值对水平承载力Pu的影响见图 5。由图可见，分段斜壁桶形基础的水平承载力Pu随着桶壁倾角β1或β2的增大而急剧增大。当β2=2°时，β1=4°时的水平承载力比β1=0°时的水平承载力增加 41.5%；当β1=3°时，β2=6°时的水平承载力比β2=0°时的水平承载力增加31.0%。

图5 桶壁倾角对水平承载力的影响Fig.5 Influence of obliquity of wall on horizontal bearing capacity of foundation

海上风机主要承受风荷载、水流荷载、冰荷载和波浪荷载，这些荷载都使底部的桶形基础承受巨大的水平力。桶形基础的水平承载力往往是其设计过程中的控制参数。本文所提出的斜壁式桶形基础，仅通过使桶壁向外倾斜一个较小的角度β1或β2，便可获得较大的水平承载力，这个规律的认识对桶形基础的优化设计有重要的帮助。

当然实际工程中，桶壁倾角β1或β2越大，施工难度也越大，故应根据水平承载力的要求选择一个合适的桶壁倾角值。

4.2 桶壁倾角β1与β2的比较分析

分段斜壁桶形基础的水平承载力Pu随着桶壁倾角β1或β2的增大而急剧增大，但能否进一步区别β1与β2的贡献度，即β1与β2中哪个参数对提高桶基水平承载力的帮助更大。为了探讨这个问题，不妨引入体积压缩率的概念。

式中：αV为体积压缩率，反映施工前后土体体积的变化幅度；V前表示桶基贯入海床过程中，被挤入桶内的土体的原始体积，即为图6中ABB′A′断面绕对称轴旋转一周所得的体积。V后为桶内体积，为施工结束后桶内土塞的体积，即为图 6 中AEFF′E′A′断面绕对称轴旋转一周所得的体积。显然，β1与β2的不同取值对体积压缩率αV的数值有重要影响。

图6 土体压缩前后体积示意图Fig.6 Schematic diagram of soil volume before and after compression

图7给出了体积压缩率αV对分段斜壁桶形基础水平承载力的影响情况。可见，体积压缩率αV越大，桶基的水平承载力越高，与β2=0°、β1变化情况下的水平承载力比β1=0°、β2变化情况下的水平承载力增长幅度更大。如体积压缩率αV均为1.2时，β1=0°、β2变化情况下的水平承载力相比（Pu）β1=β2=0°增加1.16倍，而β2=0°、β1变化情况下的水平承载力相比（Pu）β1=β2=0°增加1.64倍。因此，与β2相比，β1对提高桶基水平承载力的贡献更大。认识这一点对桶形基础构型的优化设计有重要指导作用。

另一方面，体积压缩率αV越大，海床土体被压缩的比例越大，土体与桶壁之间的摩擦力越大，使得桶基的贯入施工难度越大。因此，从施工角度来说，体积压缩率αV越小（即β1、β2取值越小）越容易施工。不同海域海床土体的含水率、孔隙比等土性参数不同，故其压缩性及与桶基的摩擦系数不尽相同。具体工程中，应对体积压缩率αV与摩擦系数的关系进行试验研究，以便确定一个合理的体积压缩率αV数值，使其既能保证正常施工，又满足桶基的承载力要求。

可见，综合考虑承载力特性与施工难易程度方面的要求，采取β2=0°、β1变化的桶基构型更合理。即推荐优先使用上部桶壁倾斜、下部桶壁直立的桶形基础构型，如图4(d)所示。

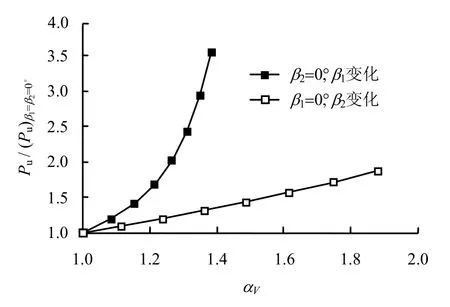
图7 体积压缩率对水平承载力的影响Fig.7 Influence of volume compression ratio on horizontal bearing capacity of foundation

4.3 地基反力比例系数m对水平承载力Pu的影响

在式（13）的推导过程中，桶侧与桶底土压力的计算均依赖于地基反力比例系数m，土性参数对桶形基础的影响也主要体现在该参数上。即地基反力比例系数m的取值是工程地质条件、海洋土物理力学参数的综合体现。

图8给出了β1=3°、β2=0°时桶基水平承载力Pu与地基反力比例系数m之间的相互关系。可见，水平承载力Pu随着地基反力比例系数m的增加而增大，并呈线性关系。从式（13）也可以看出，水平承载力Pu与地基反力比例系数m呈线性关系。

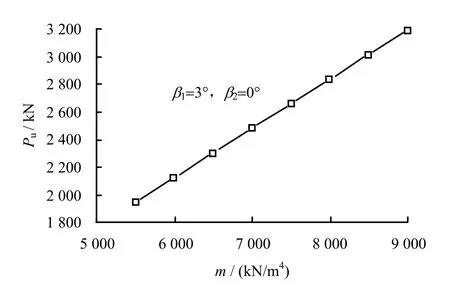
图8 地基反力比例系数对水平承载力的影响Fig.8 Influence of proportional coefficient of soil resistance on horizontal bearing capacity of foundation

实际工程中影响地基反力比例系数m的因素较多，其值难以准确测定。如在建筑桩基技术规范中指出，地基土水平抗力系数的比例系数m不仅与地基土类别有关，还与桩的类型和荷载的作用性质有关，软塑状黏性土对于预制桩和钢桩可取m=4.5～6.0 MN/m4，而对于灌注桩则取m=6.0～14.0 M N/m4。

这种m取值的大范围变动对水平承载力Pu的计算值影响较大。因此，亟需发展针对海洋土、海床地基反力比例系数m的准确确定方法，并建立相应的详细表格供查取。

4.4 桶基尺寸对水平承载力Pu的影响

β1=3°、β2=0°时水平承载力Pu与桶基顶部直径D、桶基高度H之间的相互关系见图9。可见，水平承载力Pu随着桶基顶部直径D或桶基高度H的增大而急剧增大。

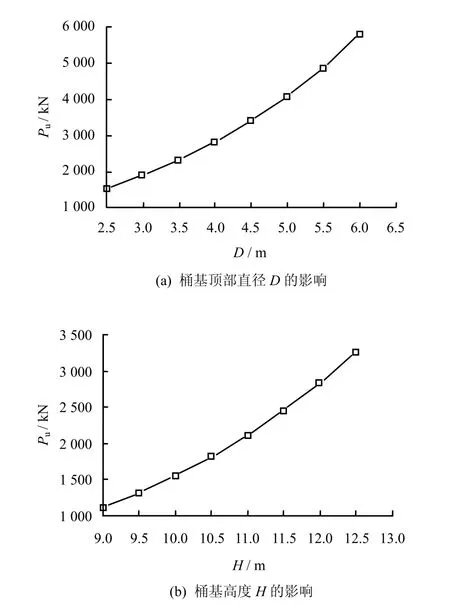
图9 桶基尺寸对水平承载力的影响Fig.9 Influence of size of bucket foundation on horizontal bearing capacity of foundation

桶基的高度与直径之比H/D是一个重要的设计参数，图10给出了β1=3°、β2=0°、D=4.0 m时H/D对水平承载力Pu的影响。可见，水平承载力Pu随着桶基高度与直径之比H/D的增大而急剧增大。但H/D越大，桶基越来越细长，制作与贯入难度越大。一般H/D的取值范围为1～3。

图10 桶基高度与直径之比对水平承载力的影响Fig.10 Influence of the ratio of height to top diameter of bucket foundation on horizontal bearing capacity

故实际工程中，桶基顶部直径D、高度H和桶壁倾角β1、β2等参数的最合理取值问题，需根据水平承载力要求、海床地质条件、土性参数、施工难易程度等综合确定。

4.5 海床深度对水平承载力Pu的影响

近海风电工程的建设与海床深度密切相关。海床越深，风机中心至桶基顶部的距离增加，即水平荷载的作用高度增加。故可用水平荷载的作用高度Lp来反映海床深度。

图11给出了β1=3°、β2=0°时水平荷载作用高度Lp对桶基水平承载力Pu的影响。Lp=180 m时的水平承载力比Lp= 1 50 m时的水平承载力降低了15.6%。桶基水平承载力Pu随着水平荷载作用高度Lp增加而急剧减小。

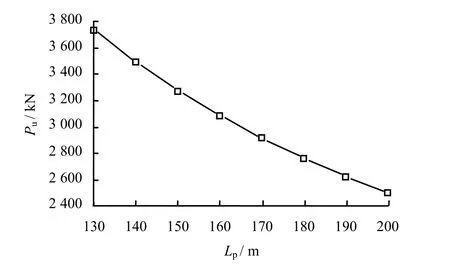
图11 荷载作用点高度对水平承载力的影响Fig.11 Influence of height of acting point on horizontalbearing capacity of foundation

可见，海床深度也是桶形基础设计中的一个重要参数。若海床较深，采用单个桶形基础难以满足要求时，可采用多桶联合基础，此时设计与计算方法更为复杂。

5 精确解与近似解的比较

前文提到，桶壁倾角对旋转点A的位置影响较小，计算中假定A点位于距桶顶2H/3处，且求解过程中对x方向、z方向的力平衡采取了简化处理。本节进一步探讨这种简化与假定的影响程度。

事实上，只有在β1=β2=β≠ 0 °情况下，不需要假定A点的位置通过上述类似推导过程可求得水平承载力的精确解，结果如下：

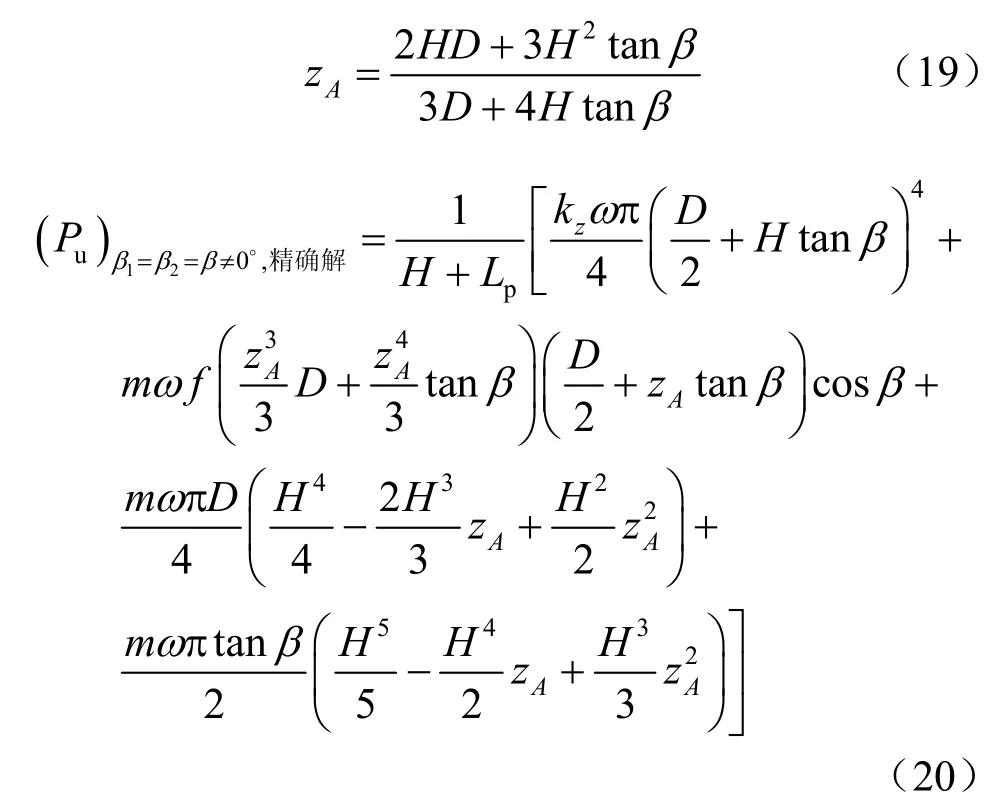
式中：zA为桶基旋转点A到桶基顶部的距离。先根据式（19）计算桶基旋转点A的深度zA，再与其他参数一起代入式（20）便得水平承载力的精确解Pu。当β=0°时，由式（20）也可推导得到式（14）。

根据桶形基础的构型可知，式（15）、（20）均为β1=β2=β≠ 0 °情况下水平承载力的计算公式，前者为近似解，后者为精确解。因此，可以通过比较式（15）、（20）的误差来考察简化与假定的影响程度。

仍以Nkossa油气田吸力锚的参数为例，计算得到旋转点深度zA与桶壁倾角β之间的相互关系，见图12。

图12 桶体旋转点深度与桶壁倾角之间的依赖关系Fig.12 Relationship between depth of rotation point and obliquity of wall

可见，桶体旋转点深度zA随着桶壁倾角β的增大略有增大，β=10°时的zA比β=0°时的zA增大5.1%。

β1=β2=β≠ 0 °情况下水平承载力的近似解与精确解比较分析见图13。可见，（Pu）式(15)/（Pu）式(20)随着桶壁倾角β的增大呈现先略增大后略减小的变化趋势，在β=6°左右（Pu）式(15)/（Pu）式(20)取得最大值1.054。也就是说，近似解与精确解的最大误差为5.4%，显然是可以接受的。且这种误差随着桶基顶部直径D或桶基高度H的减小会进一步降低。

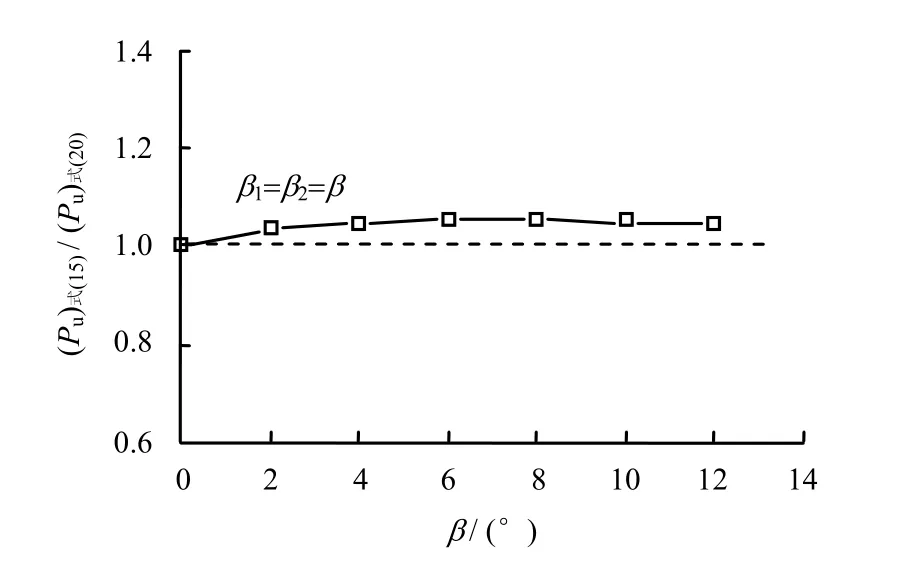
图13 β1= β2=β 时水平承载力近似解与精确解之间的关系Fig.13 Relationship between approximate solution and exact solution of horizontal bearing capacity at β1= β2=β

因此，计算中假定A点位于距桶顶2H/3处是可行的，其误差在可以接受的范围内。反之，若不通过假定A点的位置来减少未知数，从数学上就无法求解得到分段斜壁桶基的水平承载力表达式。可见这种假定做法也是必要的。下一步将结合具体试验对上述结论进行比较分析与修正。

6 结 论

（1）基于分段斜壁桶形基础的空间受力状态和基本假定，利用极限平衡法推导得到了分段斜壁桶形基础的水平承载力一般表达式，并进一步得到了4种特殊构型桶基的水平承载力计算方法。

（2）分段斜壁桶形基础的水平承载力随着上部或下部桶壁倾角的增大而急剧增大。基于体积压缩率的概念，论证并推荐优先使用上部桶壁倾斜、下部桶壁直立的桶形基础构型。

（3）分段桶形基础的水平承载力随着地基反力比例系数的增加而增大，并呈线性关系。影响地基反力比例系数的因素较多，有待发展针对海床地基反力比例系数的准确确定方法，并建立相应的表格供查取。

（4）分段斜壁桶形基础的水平承载力随着桶基顶部直径或桶基高度的增大而急剧增大，随着海床深度的增加而急剧减小。

（5）力学分析中，对桶形基础在水平承载力作用下的旋转点高度进行假定是可行和必要的，其对水平承载力的计算值影响较小。

还有待开展大尺度的模型试验对本文所提计算方法进行验证与修正。水平荷载、竖向荷载、弯矩共同作用下分段斜壁桶形基础的承载特性尚需进一步研究，且有待发展相应的施工技术与方法。

[1] 李大勇, 刘小丽, 孙宗军. 海上风电塔架基础的新型吸力锚研发[J]. 海洋技术, 2011, 30(3): 83－87.LI Da-yong, LIU Xiao-li, SUN Zong-jun. A novel type suction anchors for offshore wind turbines[J]. Ocean Technology, 2011, 30(3): 83－87.

[2] 赵世明, 姜波, 徐辉奋, 等. 中国近海海洋风能资源开发利用现状与前景分析[J]. 海洋技术, 2010, 29(4): 117－121.ZHAO Shi-ming, JIANG Bo, XU Hui-fen, et al.Exploration and application of ocean wind energy resources in coastal sea of China[J]. Ocean Technology,2010, 29(4): 117－121.

[3] 张超然, 李靖, 刘星. 海上风电场建设重大工程问题探讨[J]. 中国工程科学, 2010, 12(11): 10－15.ZHANG Chao-ran, LI Jing, LIU Xing. Exploration of major engineering problems of offshore wind farm[J].Engineering Sciences, 2010, 12(11): 10－15.

[4] 刘悦, 时志刚, 胡颖, 等. 海上风电技术特性对比分析[J].船舶工程, 2012, 34(1): 95－99.LIU Yue, SHI Zhi-gang, HU Ying, et al. Analysis on characteristic of offshore wind technology[J]. Ship Engineering, 2012, 34(1): 95－99.

[5] 黄维平, 李兵兵. 海上风电场基础结构设计综述[J]. 海洋工程, 2012, 30(2): 150－156.HUANG Wei-ping, LI Bing-bing. Reviews and comments on the design for offshore wind structures[J]. The Ocean Engineering, 2012, 30(2): 150－156.

[6] 尚景宏, 罗锐, 张亮. 海上风电基础结构选型与施工工艺[J]. 应用科技, 2009, 36(9): 6－10.SHANG Jing-hong, LUO Rui, ZHANG Liang.Foundation structure selection and construction process for offshore wind turbines[J]. Applied Science and Technology, 2009, 36(9): 6－10.

[7] ISKANDER M, EI-GHARBAWY S. Performance of suction caissons in sand and clay[J]. Canadian Geotechnical Journal, 2002, 39(3): 576－584.

[8] ZDRAVKOVIC L, POTTS D M, JARDINE R J. A parametric study of the pull-out capacity of bucket foundations in soft clay[J]. Geotechnique, 2001, 51(1):55－67.

[9] AUBENY C P, HAN S W, MURFF J D. Inclined load capacity of suction caissons[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(14): 1235－1254.

[10] HOULSBY G T, BYRNE B W. Design procedures for installation of suction caissons in sand[J]. Geotechnical Engineering, 2005, 158(GE3): 135－144.

[11] 王庚荪, 孔令伟, 杨家岭, 等. 水平载荷作用下土体与桶形基础的相互作用[J]. 工程力学, 2004, 21(2): 107－113.WANG Geng-sun, KONG Ling-wei, YANG Jia-ling, et al.Interaction of soil mass and bucket foundation under horizontal loads[J]. Engineering Mechanics, 2004, 21(2):107－113.

[12] 武科, 栾茂田, 范庆来, 等. 复合加载模式下桶形基础破坏包络面弹塑性有限元数值分析[J]. 工程力学, 2008,25(11): 156－161.WU Ke, LUAN Mao-tian, FAN Qing-lai, et al. Numerical analysis of failure envelopes of bucket foundation subjected to combined loads beased on elasto-plastic FEM[J]. Engineering Mechanics, 2008, 25(11): 156－161.

[13] TJELTA Tor-inge, STATOIL A S. Geotechnical aspects of bucket foundations replacing piles for the Europipe 16/11-E Jacket[C]//Offshore Technology Conference. Houston:[s. n.], 1995: 73－82.

[14] 袁中立, 秦延龙, 唐海燕. 浅海桶形基础平台[M]. 北京: 石油工业出版社, 2010.

[15] ZEINODDINI M, KEYVANI J, NABIPOUR M. Tapered suction caissons: A numerical investigation into their pull-out performance[J]. China Ocean Engineering,2009, 23(4): 695－707.

[16] 徐文强, 袁凡凡, 李火兵, 等. 斜壁桶形基础水平承载力的三维有限元分析[J]. 中国科学院研究生院学报,2012, 29(2): 200－205.XU Wen-qiang, YUAN Fan-fan, LI Huo-bing, et al.Horizontal bearing capacity of tapered bucked foundations based on three-dimensional finite element numerical analysis[J]. Journal of Graduate University of Chinese Academy of Sciences, 2012, 29(2): 200－205.

[17] 孙曦源, 栾茂田, 唐小微. 饱和软黏土地基中桶形基础水平承载力研究[J]. 岩土力学, 2010, 31(2): 667－672.SUN Xi-yuan, LUAN Mao-tian, TANG Xiao-wei. Study of horizontal bearing capacity of bucket foundation on saturated soft clay ground[J]. Rock and Soil Mechanics,2010, 31(2): 667－672.

[18] 施晓春, 徐日庆, 龚晓南, 等. 桶形基础单桶水平承载力的试验研究[J]. 岩土工程学报, 1999, 21(6): 723－726.SHI Xiao-chun, XU Ri-qing, GONG Xiao-nan, et al.Experimental study on horizontal bearing capacity of single bucket foundation[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 723－726.

[19] 刘振纹, 王建华, 秦崇仁, 等. 负压桶形基础地基水平承载力研究[J]. 岩土工程学报, 2000, 22(6): 691－695.LIU Zhen-wen, WANG Jian-hua, QIN Chong-ren, et al.Research on the horizontal bearing capacity of bucket foundations[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(6): 691－695.