一维对流-扩散试验各种边界条件及其统一形式解析解

张文杰，赵 培，贾文强

（上海大学 土木工程系，上海 200072）

1 引 言

压实黏土衬垫或黏土类防渗屏障广泛应用于填埋场及其他污染控制领域，除压实土料的渗透系数外，扩散和吸附性能对污染防控效果都有显著影响。室内土柱对流-扩散试验常用来研究各种黏土类屏障材料中污染物的迁移规律，通过对试验数据的拟合分析，可以确定扩散系数和阻滞因子。获取用于拟合的试验数据有两种方法：一种是截面分析，即经过一定试验历时后切片测试，获取溶质浓度沿深度变化曲线，该方法的优点是土柱不必完全击穿，因此，试验历时相对短；另一种是累积浓度法[1]，获得累积出流浓度随时间变化曲线，该法操作简单，但通常需要使出流浓度达到源浓度以获得完整的击穿曲线，因此，试验历时要长得多。试验数据的拟合多采用一维对流-扩散解析解[2-4]，然而不同边界条件对应不同的解析解，采用何种边界条件关系到数据拟合结果的正确性或者准确程度。

Shackelford[5-6]使用半无限边界解析解拟合土柱试验数据，认为土柱高度范围内溶质浓度可以用无限远处浓度梯度为0的解析解来求；Barry等[7-8]在对上文的讨论中提出不同意见，认为如果自由出流边界的溶液收集方法导致出流不连续，土柱底部应采用零浓度梯度或零浓度边界，且二者等价[9]；Rabideau等[10]认为，零浓度梯度边界不适合低渗流速度的情形，若存在垂直于扩散方向的水流，则应采用零浓度边界；余闯[11]、谢海建[12]等建立了污染物一维扩散解析解并进行验证，其下边界均采用零浓度边界；詹良通等[13]拟合土柱离心试验数据时使用了半无限边界的解析解。由此可见，国内外学者在进行土柱试验数据拟合或验证解析解时采用了不同的边界条件。边界条件到底该如何选择？使用不同边界条件解析解进行数据拟合产生的误差是否可以忽略等问题尚需进一步研究。

本文探讨了土柱试验通常涉及到的边界条件及其适用条件，给出了统一形式的边界条件，并求得统一形式的有限厚度土层对流-扩散-吸附解析解，通过算例对比了各边界条件解析解计算结果的差异，分析了因采用不同边界条件进行数据拟合产生的误差。

2 土柱试验的边界条件

一维土柱试验中，因对流和扩散引起的溶质通量可表达为[5]

式中：J为土孔隙流体中溶质通量；θ为体积含水率，对于饱和土θ等于孔隙率n；v为孔隙水流速，通常认为，v=V/θ，V为达西流速；cr为土孔隙流体中溶质浓度；z为从土柱顶面开始算起的溶质运移距离（向下为正）；t为时间；D为水动力弥散系数，是同时考虑分子扩散和机械弥散的综合参数。

考虑溶质质量守恒，由连续性条件知：

式中：Rd为考虑线性吸附的阻滞因子。

联立式（1）、（2），即得到考虑对流、扩散和吸附的土柱中溶质一维运移控制方程：

若忽略背景浓度，则初始条件为

为便于拟合分析，通常试验的土柱顶面采用溶液循环方法，或放置足够体积的已知浓度溶液，以保证在试验过程中入流浓度不变或近似不变，因此，上边界条件为

式中：0+为土柱上表面内侧的入流边界。

底边界条件较复杂，根据试验方法和底部出流条件，分为零浓度边界、自由出流边界、半无限边界、柯西边界4种。

2.1 零浓度边界

当土柱底部有与底面平行流动的纯水，流速和流量足够时，流水将溶质从土柱底面带走的速度足够快，或者土柱底面处的流动不连续，此时底面边界可设置为零浓度边界：

式中：H为试样厚度。

此时，底面孔隙中的溶质能完全扩散至边界外，这一边界条件也称Dirichlet边界，试验中土柱底部以纯水循环可（接近）实现此边界。在试验初期，溶质远未迁移至底面附近，底面处浓度和浓度梯度均为 0，可用此边界条件对应的解析解拟合试验数据；而当试验进行足够长时间后，此边界条件对应的底面处浓度梯度为（负）无穷大，而浓度仍为0，这与实际不符，因为土柱击穿后底面内边界会有少量溶质积聚，特别是土柱内溶质迁移以对流为主导时，此时内边界浓度不为 0。因此，对应的边界条件应表述为

式中：H+为土柱底面外边界。

2.2 自由出流边界

当底面处仅水压力梯度不为 0，即扩散作用相比对流来说可以忽略时，定义底部为自由出流边界，此时出流溶质的浓度梯度为0：

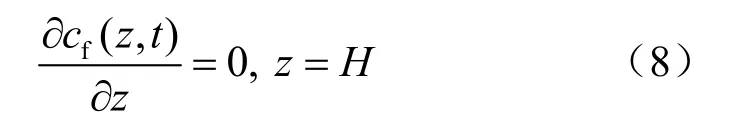
式中：cf为某时段内按出流量计算的平均浓度，当土柱内溶质迁移以对流为主导时，cf与cr接近，随对流作用比例下降，cf与cr之间的差异增大，流量为0即纯扩散时cf无意义。用Péclet特征数Pe表示对流与扩散在溶质迁移中所占比例，Parlange等[14]认为，当Pe＞4时，近似有cf=cr，此时边界条件为

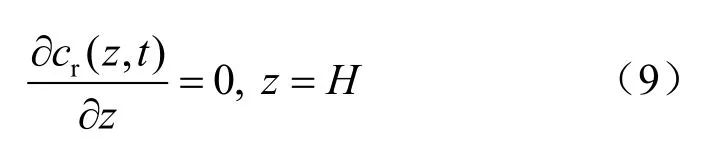
这一边界也称为Neumann边界。通常土柱试验在完全击穿（以源浓度出流）之前，底面后出流的溶液浓度大于先前出流的溶液，因此，浓度梯度不为0，但若底边界处孔隙中的溶液能被及时吸走，则底边界处没有浓度差，即不发生扩散，此时可认为浓度梯度为 0，故此边界也被称为完全吸收边界，对应一个理想状态。通常粗颗粒土料的土柱试验较多采用这一边界条件下的解析解进行拟合，但试验时应控制对流为主导，并注意底部浓度梯度，以接近这一边界的上述物理本质，而当土料渗透系数很小，以扩散为主导时，边界处孔隙中的溶液不易排出，不宜采用此边界。

2.3 半无限边界

半无限边界是指在无限深度处浓度梯度为0：

土柱试验中若土柱底部与收集到的出流溶液相接触，且出流溶液的浓度测量采用下面两种方式：一是出流达到一定体积后从底部移除并测量将之作为这段时间的平均出流浓度；二是持续测量累积浓度，在这两种情况下，底边界内外浓度均不同，即浓度梯度不为 0。边界条件式（10）对应的解析解在z=H处的浓度梯度不为0，取某时刻t的浓度计算值可拟合浓度剖面，取z=H处的浓度计算值可拟合平均出流浓度，或经变换后用于拟合累积浓度[1]。虽然式（10）定义无限远处的边界，但拟合时流速v已知，此定义与对流无关，拟合造成的误差仅来源于底边界的扩散速度，即式（10）确定的底边界处浓度梯度值与试验操作对应的真实浓度梯度之间的误差。

2.4 柯西边界

由上述可知，当土柱底部被击穿时，无论零浓度边界（对应浓度梯度为无穷大）还是自由出流边界（对应浓度梯度为 0）均基于理想假定，实际上土柱试验在击穿后底边界处浓度不为 0，而浓度梯度一般处于0与负无穷大之间，且出流浓度和浓度梯度并非固定值，这样的边界称为混合边界，即Cauchy边界：

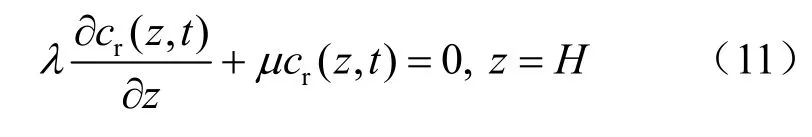
式中：μ、λ为描述边界条件的参数。λ正比于扩散系数，通常不为 0，这样，当接触参数μ趋向无限大，式（11）退化成零浓度边界，当μ=0，式（11）退化成零浓度梯度边界，μ取其他值时表示底边界处浓度和浓度梯度均不为 0，且浓度梯度值随浓度而变化。因此，式（11）可以看做各边界条件的统一形式。式中的两个参数μ、λ实际上可用一个值μ/λ表示（单位为1/m），称为Cauchy边界参数。

3 统一形式边界条件下的解析解

由式（3）～（5）、（11）定义的数学模型无法直接求解，可通过变换式

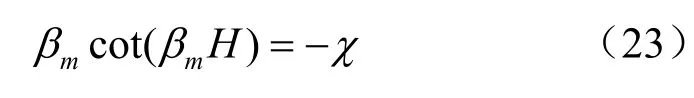
Péclet数Pe常对有限域级数解的敛散性有较大影响，满足收敛所需的项数m随Pe增大而增大，依据此级数形式解析解编制简单程序，其中m取20 000，可计算Pe=30对流为主导的问题。

4 不同边界条件解析解对比及拟合误差分析

式（21）对应的边界条件是前述各种边界条件的统一形式，因此，可以方便地对比不同边界条件下解析解的差别。算例中取土柱高度H=5 cm；孔隙水流速v= 3 × 1 0-6cm/s；水动力弥散系数D=5×10-6cm2/s；忽略吸附作用，取Rd=1；试样顶部为常浓度边界，底部分别取上述各种边界；模拟溶质运移时间分别为2、9 d。计算得到2、9 d后溶质浓度分布剖面分别如图1(a)、1(b)所示。

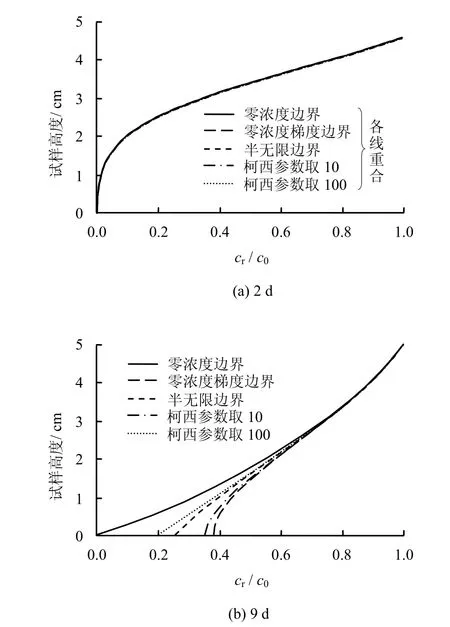
图1 不同底部边界条件解析解对比Fig.1 Analytical solutions for different boundary conditions

图1(a)为溶质运移2 d后的浓度剖面线，可见土柱未被击穿（击穿指试样底部出流达到某个浓度值或相对浓度值），图中各剖面线重合，说明此时各种边界条件下解析解结果相同。此时若使用解析解拟合试验数据，使用各边界条件均可，不存在差别。但需要指出的是，为了获得尽可能多的有效（非零的）数据点，以减小数据拟合误差，土柱试验通常进行到底部达到一定击穿浓度才终止。

图1(b)为溶质运移9 d后的浓度剖面线，此时土柱已被击穿，可见在试样上半部分各边界对应解析解的浓度基本接近，在试样下半部分各解差异较大，其中零浓度边界对应的底部浓度最低，零浓度梯度边界对应的浓度最高，半无限边界、柯西参数μ/λ取10和100的边界对应的浓度居中。如前所述，零浓度边界假定底部能充分扩散，与式（21）中μ/λ=∞的解相对应；半无限边界假定底边界处存在有限的扩散作用，本算例中与μ/λ=57的解答一致；零浓度梯度边界假定扩散为0，与μ/λ=0的解相对应。因此，计算所得底部边界处的浓度随底部浓度梯度的增大而减小，也随柯西边界参数μ/λ的增大而减小；μ/λ越大，代表底边界处扩散在溶质迁移中所占比例越大，亦即底部浓度梯度越大。

试验采取何种边界条件解析解拟合，应根据试验时底部边界处的具体情况，即综合考虑对流-扩散比例和浓度梯度情况来确定。若底部保持为纯水，则击穿后浓度梯度很大，接近零浓度边界的情形；若扩散为主导，土样底部接触出流溶液，测出流溶液的累积浓度，此时边界浓度梯度大于下为无限土层的情形，则采用μ/λ取较大值（如图1中取100）的边界；若土样底部接触出流溶液，出流溶液移除频率较高，则对应半无限边界；若土样底部不接触出流溶液，土的渗透性较好，底部孔隙中的溶液不积聚，则采用μ/λ取较小值（如图1中取10）的边界；若底部边界处扩散可以忽略，即符合自由出流条件，则采用零浓度梯度边界。

如某土柱试验为黏土试样，土样底部为透水石接出流管，则属前述底部接触出流溶液且出流溶液能及时移走的情形，对应（或接近）半无限边界。此处目的在于分析使用不同边界条件解析解拟合造成的误差，为了排除试验操作及数据本身离散性的误差影响，以半无限边界解析解数据为基准。取土柱高度H=5 cm，采用惰性溶质（取Rd=1），已知孔隙水流速v= 1 .7× 1 0-6cm/s，试验20 d后的溶质浓度分布剖面如图2中圆点所示，要拟合求水动力弥散系数D。拟合需满足所有基准点处浓度拟合值与基准值之差的平方和最小，编制简单程序采用步进搜索方法[15]求得最佳拟合值。使用无限边界的解析解拟合得到D=1.45 × 1 0-6cm2/s（基准解）。若用零浓度边界拟合，得到D=1.67 × 1 0-6cm2/s，偏大15%，且拟合残差较大；若用零浓度梯度边界拟合，得到D=1.32×10-6cm2/s，虽然拟合残差很小，但拟合值仍偏小 9%，误差不容忽视。因此，根据试验的边界条件合理选择解析解进行数据拟合，不仅是理论上的需要，也是数据处理准确性的需要。

图2 不同底部边界条件解析解拟合结果Fig.2 Fitting curves of analytical solutions for different boundary conditions

5 结 论

（1）土柱试验数据可用零浓度边界、零浓度梯度边界、半无限边界对应的解析解来模拟，每一种边界条件都与实际的试验条件相对应。

（2）柯西边界可看做各种边界条件的统一形式，此边界条件下的微分方程无法直接求解，通过引入变换式和辅助问题，求解得到适用于各种底边界条件的有限厚度土层中考虑对流、扩散、吸附的污染物运移统一形式解析解。

（3）算例表明，土柱未被击穿时各边界条件解析解无差别；土柱被击穿后，越靠近土柱底面，各种边界条件解析解计算结果差异越大，底面处浓度值随柯西参数μ/λ的增大而减小，μ/λ越大，代表底边界处扩散在溶质迁移中所占比例越大，亦即底部浓度梯度越大，这是选择何种边界条件解析解进行试验数据拟合的依据。

（4）拟合试验数据求水动力弥散系数时，根据试验时土柱底部的对流-扩散比例和浓度梯度具体情况，选择相应的边界条件解析解，不仅是理论上的需要，也是显著减小误差的需要。

[1] SHACKELFORD C D. Cumulative mass approach for column testing[J]. Journal of Geotechnical Engineering,1995, 121(10): 696－703.

[2] PARKER J C, VAN GENUCHTEN M T. Flux-averaged and volume-averaged concentrations in continuum approaches to solute transport[J]. Water Resources Research, 1984, 20(7): 866－872.

[3] SHACKELFORD C D. Transit-time design of earthen barriers[J]. Engineering Geology, 1990, 29(1): 79－94.

[4] ACAR Y B, HAIDER L. Transport of low-concentration contaminants in saturated earthen barriers[J]. Journal of Geotechnical Engineering, 1990, 116(7): 1031－1052.

[5] SHACKELFORD C D. Critical concepts for column testing[J]. Journal of Geotechnical Engineering, 1994,120(10): 1804－1828.

[6] SHACKELFORD C D, PATRICK L R. Solute break through curves for processed kaolin at low flow rates[J].Journal of Geotechnical Engineering, 1995, 121(1): 17－32.

[7] BARRY D A, ANDERSON S J. Discussion of ‘Critical concept for column testing'[J]. Journal of Geotechnical Engineering, 1996,122 (1): 84－87.

[8] BARRY D A, ANDERSON S J. Discussion of ‘Solute break through curves for processed kaolin at low flow rates'[J]. Journal of Geotechnical Engineering, 1996,122 (9): 781－785

[9] BARRY D A, SPOSITO G. Application of the convection-dispersion model to solute transport in finite soil columns[J]. Soil Science Society of American Journal, 1988, 52(1): 3－9.

[10] RABIDEAU A, KHANDELWAL A. Boundary condition for modeling transport in vertical barriers[J]. Journal of Environmental Engineering, 1998, 124(11): 1135－1139.

[11] 余闯, 方冬芳, 杜广印, 等. 均质土中考虑溶质蜕变效应的污染物迁移模型的解析解[J]. 东南大学学报(自然科学版), 2012, 42(6): 1206－1210.YU Chuang, FANG Dong-fang, DU Guang-yin, et al.Analytical solution on pollutant migration considering solute decay in homogeneous soil[J]. Journal of Southeast University ( Natural Science Edition) , 2012,42(6): 1206－1210.

[12] 谢海建, 唐晓武, 陈云敏, 等. 原始土层影响下成层介质污染物一维扩散模型[J]. 浙江大学学报(工学版),2006, 40(12): 2191－2195.XIE Hai-jian, TANG Xiao-wu, CHEN Yun-min, et al.One-dimensional model for contaminant diffusion through layered media[J]. Journal of Zhejiang University (Engineering Science), 2006, 40(12): 2191－2195.

[13] 詹良通, 曾兴, 陈云敏. 惰性污染物在低渗透性黏土中弥散作用离心模拟的相似研究[C]//第七届全国岩土工程物理模拟学术研讨会论文集. 杭州: [s. n.], 2013: 131－137.

[14] PARLANGE J Y, STARR J L, VAN GENUCHTEN M T,et al. Exit condition for miscible displacement experiments[J]. Soil Science, 1992, 153(3): 165－171

[15] 张文杰, 贾文强, 张改革, 等. 黏土-膨润土屏障中氯离子对流扩散规律研究[J]. 岩土工程学报, 2013,35(11): 2076－2081.ZHANG Wen-jie, JIA Wen-qiang, ZHANG Gai-ge, et al.Research on advection and dispersion of Cl-in claybentonite barriers[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2076－2081.