多道次双点渐进成形数值模拟与实验研究*

曹 江 ，王秋成* ，邱 磊 ，李 宁 ，魏瑞晖

(1．浙江工业大学机械工程学院，浙江杭州310014;2．杭州博冷科技有限公司，浙江杭州310019)

0 引 言

传统的金属板料成形技术广泛地应用于航空、航天、汽车、医疗器械、饮料容器等行业，由于模具制作周期长、制作费用比较高，故适用于产品定型后的大批量生产。当前对产品零件的需求日益呈现出多品种、小批量等特点，企业如何快速适应市场需求越来越成为获得竞争优势的关键。而近年来新出现的金属板料渐进成形技术(incremental forming，IF)，是一种无模成形(dieless forming)新技术，可明显缩短新产品开发周期，降低新产品制作成本，并具有很高的工艺柔性，可获得形状非常复杂的零件外形［1］。根据成形中与板料接触点的个数，可渐进成形技术可分为两类［2］:单点渐进成形(SPIF)和双点渐进成形(TPIF)。而根据渐进成形时所采用的道次数目，又可以将其分为单道次成形和多道次成形。相比单点渐进成形方法，双点渐进成形增加了一个全形或局部的支撑模具，且在成形的过程中，需要夹持装置随工具头同步向下移动或者凸模向上运动。根据Silva M B 等［3］学者的研究成果，双点渐进成形零件在成形极限和成形精度上均高于单点渐进成形;双点渐进成形更适应于商业上制作复杂零件［4］。

对于单道次渐进成形，零件厚度分布遵循余弦定律。根据余弦定律可知，当用于成形的板料越薄，成形角度越大时，成形零件越容易出现破裂现象，因此薄板直壁件成形一直是渐进成形研究中的一个难点问题［5］。当前，针对薄板陡角零件的渐进成形，多道次成形工艺是一种有效的解决方法。采用多道次渐进成形方法，通过引入更多的变形材料，使得某些局部材料的减薄现象得到减缓，从而制作出厚度分布更加均匀的陡角度成品。近年来，国内外许多学者开展了多道次渐进成形的相关研究，Skjodt M 等［6］采用多道次成形方法成功制作了球形件和直筒形样件，国内沈黎萍等［7］也成功制作了球形件，而周六如等［8］成功制作了方盒形样件，以上研究缺乏对多道次渐进成形机理与变形规律的深入研究，以及成形路径的优化设计等。

本研究针对多道次双点渐进成形中材料变形规律问题，建立典型圆锥台件双点渐进成形有限元模型。

1 多道次双点渐进成形数值模拟

1．1 材料与样品

本研究采用的板料为1060 圆形铝板，直径为160 mm，厚度为1 mm。板料参数如表1 所示。

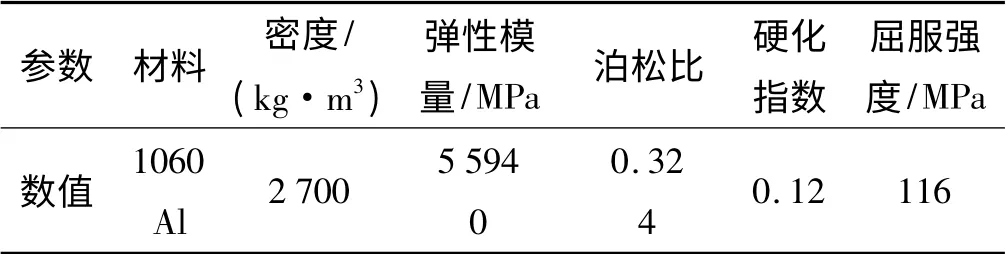
表1 材料参数

成形的目标零件如图1 所示。

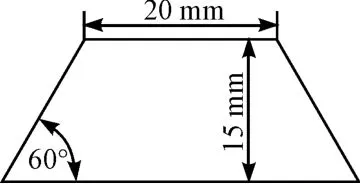
图1 目标零件

1．2 有限元模型的建立

本研究采用有限元软件ANSYS/LS-DYNA 作为数值模拟的平台，所建立的双点渐进成形有限元模型如图2 所示。

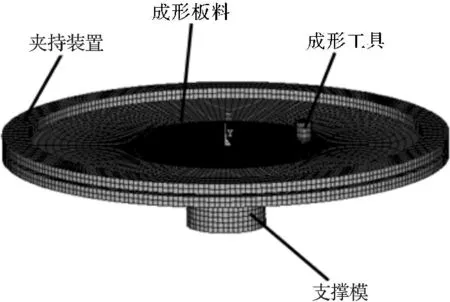
图2 双点渐进成形有限元模型

结合双点渐进成形过程的特点，夹持装置、支撑模具和成形工具头均不参与变形，因此本研究采用刚体模型;板料的单元类型选用shell163 显式壳单元，材料模型为三参数Barlat 材料模型［9］，夹持装置、支撑模具和工具头则均采用solid164 显式实体单元;综合模拟的精度和成本，选择映射法划分网格，将零件成形区域的网格大小设为1．5 mm，非成形区域设为3 mm，夹持装置、支撑模具和工具头的网格大小均设为2 mm。

结合成形特点，有3 个约束和3 个接触对需要定义。约束工具头的3 个平动自由度，夹持装置和支撑模具全约束;3 个接触对分别为板料与工具头、板料与夹持装置、板料与支撑模具，均为面面接触，由于工具头和板料的接触部位会进行良好的润滑，属于边界摩擦类型，摩擦系数取0．1，在板料与夹持装置、板料与支撑模具之间则无润滑条件，属于干摩擦，摩擦系数取0．25。

1．3 工具头与夹持装置运动轨迹的加载

工具头运动轨迹的加载是板料渐进成形模拟中的一个难点。在ANSYS/LSDYNA 中通过将三维运动分解为关于时间参数的3 个平面运动T－X、T－Y 和TZ 进行加载，X、Y、Z 的坐标可以从已获得的成形轨迹中直接提取，对于时间T 参数则要结合实际加工及有限元计算精度和成本进行设置。本研究进行的是多道次成形，还涉及到轨迹的衔接问题，通过直接将前后道次工具头X、Y、Z 的坐标进行合并，然后分别进行加载，可获得3 个时间历程曲线，四道次成形时的曲线如图3(a)、3(b)、3(c)所示。对于双点渐进成形，在实际成形过程中，夹持装置会同步向Z 向运动，因此除了对工具头轨迹的加载外，还需要给出夹持装置的运动轨迹，在第一道次加工时夹持装置的运动轨迹为工具头Z 向轨迹，当第一道次加工完成后，后续道次夹持装置位置保持不变，夹持装置四道次成形时间历程曲线如图3(d)所示。相比等高轨迹，螺旋轨迹在层与层之间不存在下刀问题，无压痕，成形质量更好，故选用螺旋轨迹进行成形模拟，而由于通用的CAM 软件无法直接生成该类型加工轨迹，本研究通过Matlab 编程的方法来获取圆锥台件多道次双点渐进成形下的螺旋加工轨迹。

图3 工具头与夹持装置运动轨迹时间历程曲线

2 多道次双点渐进成形路径设计

2．1 多道次渐进成形路径规划遵循的原则

(1)顺逆相间原则。采用顺逆相间原则将可以有效地避免所加工的零件出现扭曲现象，以及材料单向堆积现象，因此，针对相邻的两个道次应尽量采用相反方向的轨迹。

(2)变形合理原则。多道次渐进成形，理想情况应是每一道次的变形量合理且均匀。在渐进成形过程中，成形的影响因素较多，只通过参数的选择难以达到对成形的定量控制，因此，除了要选取合理的加工参数外，还要给每一道次分配合理的变形量。在多道次成形中，变形量的合理分配很大程度取决于所选取的成形角度，因为成形角度与零件的壁厚密切相关。

2．2 多道次双点渐进成形路径设计方案

本研究对壁角为60°的典型圆锥台件分别进行单道次、两道次和四道次成形，对两道次和四道次成形均设计了两种方案，该方案如图4 所示，两道次成形方案Ⅰ和Ⅱ的间隔角度分别为30°和15°，四道次成形方案Ⅰ按固定间隔角度设计，固定为10°，方案Ⅱ则按变间隔角度设计，随着成形角度的增大，逐渐减小间隔角度，分别为15°、10°和5°。为遵循顺逆相间原则，前、后道次的成形轨迹均按相反方向设计。

图4 两道次和四道次成形路径设计方案

模拟中所采用的成形工具头直径为6 mm，成形轨迹为螺旋轨迹，螺旋轨迹最重要的两个参数是螺距和步进旋转角［10］，螺距设为0．75 mm，步进旋转角度设为1°，考虑加工速度平稳，以单个螺距来计算，匀速走完一个螺距为3．6 s。

3 数值模拟结果分析

3．1 节点流动分析

通过绘制节点流动曲线图，可以观察到多道次成形过程中的材料流动规律。根据四道次成形方案Ⅰ，分别提取第一、二、三道次及成形结束后，在中心XZ截面上各节点坐标，绘制各道次的半截面曲线，并间隔几个节点，将各道次对应的节点采用虚线连接，该虚线即为节点流动曲线(曲线图如图5 所示)。由图5 可知，在第一道次时，节点几乎没有径向移动，从后续道次开始，各节点明显向内部移动，那么材料会从较大的圆周上流动到较小的圆周上，周向的应变将发生明显负增长。

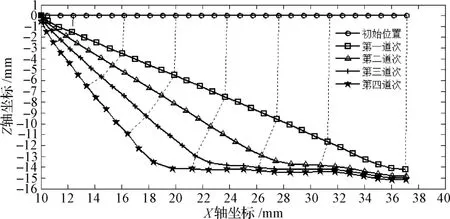
图5 四道次方案Ⅰ节点流动曲线示意图

为了比较不同道次数目和道次设计下材料流动情况，本研究取零件斜壁区域对应的相同节点号，绘制该节点随时间在X 方向上的位移曲线(曲线图如图6 所示)。由图6 可知，在单道次成形中节点位移量很小，而随着成形道次增多，节点流动非常明显，则说明从非零件形状区域流入零件形状区域的材料越多，同时发现，在相同道次不同间隔角度下，节点径向移动量基本相同。这说明成形道次数目是材料径向流动的最主要影响因素。

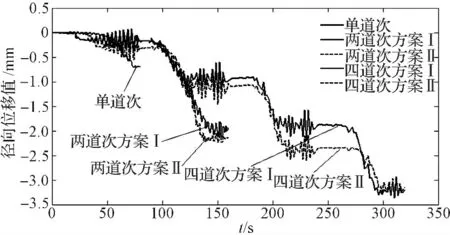
图6 节点随时间变化的位移曲线图

3．2 应变分析

通过对应变的分析，可进一步了解多道次双点渐进成形下的材料变形规律。本研究通过选取零件斜壁相同位置的单元，绘制随时间变化的应变曲线图(曲线图如图7 所示)。由图7 可知，在单道次成形中，第一主应变迅速增长为一个较大的数值，第二主应变几乎为零，而在两道次和四道次成形中，第一主应变和第二主应变均随着成形道次的增多不断增大，且处在同一量级，这进一步证实了3．1 节中周向应变负增长的情况。

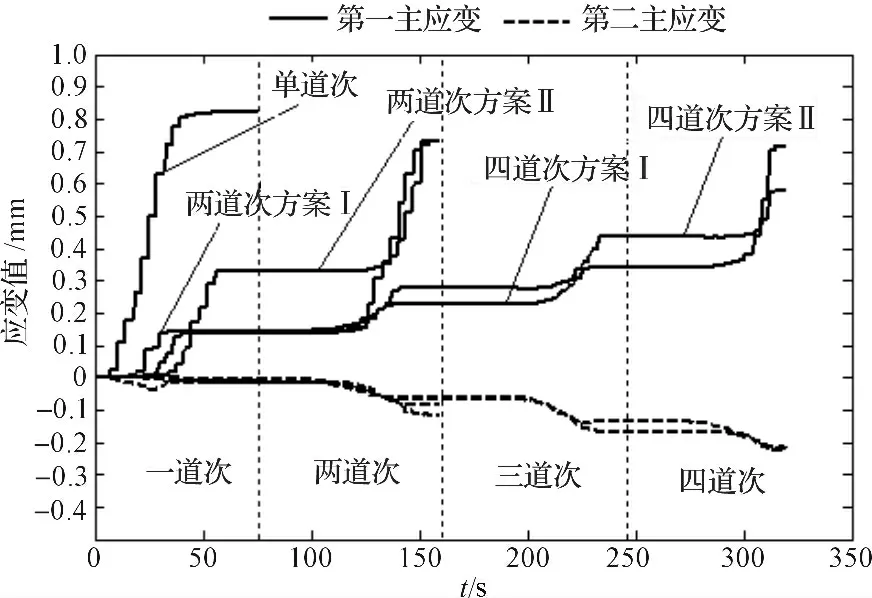
图7 随时间变化的应变曲线图

另外，本研究通过对比两道次的两个方案发现，最大第一主应变和最大第二主应变值差异均较小;对比四道次的两个方案发现，最大第二主应变值差异较小，而方案Ⅰ的最大第一主应变值则要明显高于方案Ⅱ，这是由于在前三道次时，方案Ⅰ的成形角度均未超过方案Ⅱ，第一主应变值始终低于方案Ⅱ，而进行第四道次时，第一主应变值则迅速增长超过方案Ⅱ的第一主应变值，这说明随着成形道次的增多，成形角度对应变值的影响增大。

3．3 壁厚分析

根据零件壁厚分布情况，可以直接对道次数目的影响和路径设计的合理性进行评估。过中心XZ 截面方向零件单元壁厚变化曲线图如图8 所示。可以发现，随着成形道次的增多，最小壁厚值不断增大，如相比单道次成形，两道次和四道次成形最小壁厚分别提高了约25%和50%，壁厚分布的均匀程度也不断提高。同时还发现，对于两道次成形方案Ⅰ和方案Ⅱ，斜壁厚度分布差异很小，最小壁厚分别为0．521 mm 和0．534 mm，仅相差约2．6%，而对于四道次成形的两种方案，方案Ⅱ和方案Ⅰ的最小壁厚分别为0．642 8 mm和0．597 7 mm，采用方案Ⅱ的最小壁厚提高约7．5%，斜壁厚度分布更均匀。因此，随着成形道次增多，成形角度对壁厚分布均匀性的影响越明显。

图8 截面单元壁厚分布比较图

4 实验验证

基于本课题组开发的渐进成形专用机床［11］，笔者采用螺旋进刀方式，以机床润滑油作为润滑剂，对模拟中各个方案进行渐进成形实验;本研究采用的材料参数与模拟中相同，工具头直径为6 mm，加工速度按照走完一个螺旋3． 6 s 来设置。在实验板料上印制2 mm的圆形网格，并在同一截面方向，从中心点开始等距离制作红点标记，有网格和红点标记的一面为非成形面。

采用四道次方案Ⅱ双点渐进成形的圆锥台如图9所示。观察零件非成形面的圆形网格变化可知，参与零件成形的区域，圆形网格在周向的直径均产生不同程度减小，且在零件斜壁开口处，周向直径减小达到最大，这与模拟中第二主应变的分布情况相同(分布云图如图10 所示)。本研究采用游标卡尺测量实验网格数据，通过取对数计算最大第二主应变值约为－0．2 mm，与模拟误差约为9%，实验和模拟结果基本相符。

图9 采用四道次方案Ⅱ实验成形的圆锥台

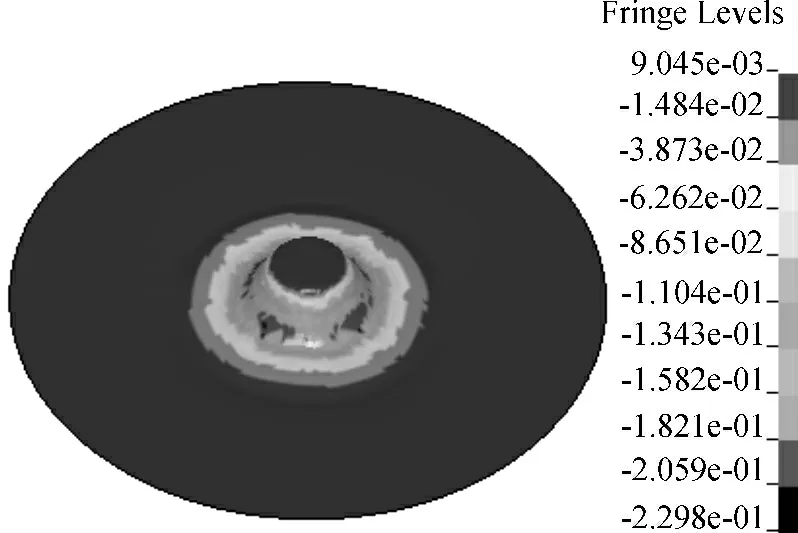
图10 四道次方案Ⅱ模拟结束后第二主应变分布云图

本研究采用游标卡尺测量各红色标记点的径向距离，并根据各点初始位置计算所产生的径向位移值，各方案下各标记点径向位移值的比较如图11 所示。可发现各标记点径向移动值均随着成形道次的增多而增大，对四道次成形的两种方案，各标记点径向位移值相差很小，对两道次的两种方案，由于方案Ⅰ参与变形的材料面积大于方案Ⅱ，则在7 号点之后将没有可比性，而在7 号点之前两方案各标记点径向位移值基本相同，因此验证了模拟中得出的成形道次数目是材料径向流动的主要因素。

图11 各标记点径向位移值的比较

针对实验成形零件，沿着中心截面方向，并间隔相同距离测量斜壁厚度，测量设备为专用的厚度计(包括一个测量表和一个顶针)，将测量结果绘制成厚度变化曲线图(曲线图如图12 所示)，可发现成形道次越多，最小壁厚越大，壁厚分布也越均匀，且成形角度对壁厚分布均匀性的影响增大。取四道次方案Ⅱ下的模拟和实验斜壁厚度变化曲线进行比较的结果如图13 所示。由图13 可知，壁厚变化规律一致，且最大壁厚误差控制在5%以内，因此可认为模拟与实验结果基本吻合。

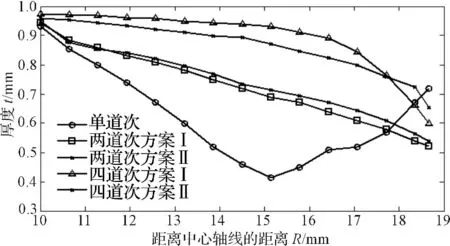
图12 各成形零件斜壁厚度分布的比较

5 结束语

(1)通过以上单道次、两道次和四道次双点渐进成形模拟，研究结果表明，多道次双点渐进成形中材料产生明显的径向流动，在周向方向的应变，特别是零件开口区域，出现明显的负增长;成形道次数目是材料径向流动的主要影响因素，随着成形道次增多，材料径向流动增大;同时，成形道次越多，零件最小壁厚越大，厚度分布均匀性越好，且成形角度对壁厚分布均匀性的影响增大;

图13 模拟和实验零件斜壁厚度分布比较

(2)考虑成形角度影响的变间隔角度路径设计方法，可提高多道次双点渐进成形零件壁厚分布均匀性，且成形道次越多作用越明显。

(3)在成形板料表面印制圆形网格和制作标记点进行验证实验，通过观察网格变化、以及对各标记点的径向移动和对零件斜壁厚度值的测量比较发现，模拟结果与实验结果基本吻合。

［1］CAO J，XIA Z C，GUTOWSKI T G，et al． A Hybrid Forming System:Electrical-Assisted Double Side Incremental Forming (EADSIF)Process for Enhanced Formability and Geometrical Flexibility［R］． Northwestern University，2012．

［2］JESWIET J，MICARI F，HIRT G，et al． Asymmetric single point incremental forming of sheet metal［J］． CIRPAnnals-Manufacturing Technology，2005，54(2):88-114．

［3］SILVA M B，MARTINS P A F． Two-point incremental forming with partial die:theory and experimentation［J］． Journal of Materials Engineering and Performance，2013，22(4):1018-1027．

［4］ATTANASIO A，CERETTI E，GIARDINI C，et al． Asymmetric two points incremental forming:improving surface quality and geometric accuracy by tool path optimization［J］．Journal of Materials Processing Technology，2008，197(1):59-67．

［5］王 莉，莫健华，黄树槐． 金属薄板直壁件数字化渐进成形过程的实验研究［J］．锻压技术，2004(6):9-11．

［6］SKJODT M，BAY N，ENDELT B，et al． Multi stage strategies for single point incremental forming of a cup［J］． International Journal of Material Forming，2008，1(1):1199-1202．

［7］沈黎萍，高锦张，蒋 松，等．板料渐进成形半球形件的路径研究［J］．锻压技术，2010，35(6):40-44．

［8］周六如．基于数控渐进成形技术的方形盒成形工艺［J］．锻压技术，2009(4):65-68．

［9］高锦张．板料数控渐进成形技术［M］．北京:机械工业出版社，2011．

［10］朱 虎，扶建辉，姜在宽．金属板材数控渐进成形螺旋线轨迹生成［J］．农业机械学报，2009(10):223-226．

［11］WANG Qiu-cheng，HU Hai-han． Experimentation and design of prototype device for three point incremental forming［J］． Applied Mechanics and Materials，2014(494):579-582．