全地形排爆机器人运动机构设计研究*

李 波 ，张 瑾 ，李国栋

(1．中国兵器装备集团上海电控研究所，上海200092;2．杭州电子科技大学机械工程学院，浙江杭州310018)

0 引 言

排爆机器人是指能代替人到不能去或不适宜去的有爆炸危险的环境中，直接在事发现场进行侦察、排除和处理爆炸物及其他危险品，也可对持枪、持械的恐怖分子实施有效攻击的机器人。排爆机器人的研制始于20 世纪60年代，随着国际上反恐形势日趋严峻和反恐斗争的深入，特别是“911”恐怖袭击事件以来，国内外的一些大公司、大学及科研院所，如美国的Remotec、iRobot，英国的P．W．Allen、ABP，德国的Telerob，国内的中科院沈阳自动化研究所、北京航空航天大学、上海交通大学等［1-2］，都先后从事相关系统和技术研究，并取得了卓有成效的进展。

排爆机器人在实际运行中受地形限制较大，如何实现全地形环境下的可靠运行，是国内外均在努力的方向。

本研究拟完成相关动力系统参数论证计算，并利用有限元方法分析主要传动系统器件参数，在此基础上设计一台高性能排爆机器人运动机构。

1 排爆机器人运动机构设计原理

机器人要在各种复杂地形下行走，楼梯、斜坡、障碍物是一定要克服的3 种地形要素。如果机器人的运动机构能通过上述3 种地形，就能在全地形条件下畅通无阻。

本研究针对以上设计需求，分析几种常用运动机构:

(1)轮式机构。该机构结构简单，速度快，易控制，被广泛应用在各种车辆上。但由于车轮与地面接触面积小，在软、湿路面上，易产生沉陷和打滑，且越障能力不足，不能独立完成复杂地形的移动［3］。

(2)履带式机构。该机构与地面接触面积大、压强小、转弯半径小，牵引附着性能、越野机动性、爬坡越沟性能均优于轮式，但具有速度慢、减振差等缺点［4］。

(3)轮履复合机构。兼具以上两种机构特点，既能在平整路面上快速移动，也能在沟壑纵横的道路上运行［5］。

本研究设计要求机器人最大移动速度为1．6 m/s，能上、下不超过30°的斜坡(楼梯)，跨越400 mm 壕沟，越过250 mm 高的障碍物，对机器人适应地形的能力提出了较高要求。经过初步分析，笔者决定采用六履带四轮复合式运动机构［6］。翻转臂履带轮的直径小于车轮，在高速运动时，前、后翻转臂均收起，只有车轮着地，因而可以高速行驶。

排爆机器人总装图如图1 所示。机器人在上、下楼梯或越障时，前、后翻转臂放下起辅助支撑车轮向上/向下移动作用，完成攀爬功能。两侧车轮拆除后，车体能作为履带式机构越过部分狭窄障碍物。

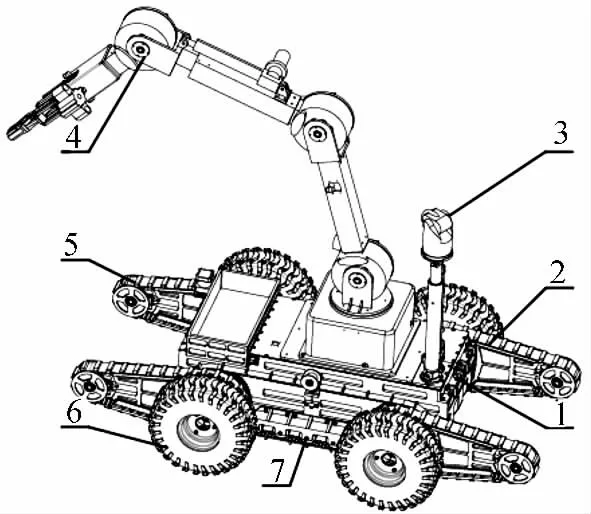
图1 排爆机器人总装图

2 排爆机器人运动机构参数计算

2．1 机器人动力系统的组成

机器人主体移动机构由一对主履带、翻转臂所组成，主履带通过两台后置伺服电机驱动，翻转臂通过前后各一台伺服电机驱动。

主驱动系主要由锂电池、直流无刷电机、集成式行星减速机、锥齿轮副、主驱动轮等组成，其原理如图2所示。

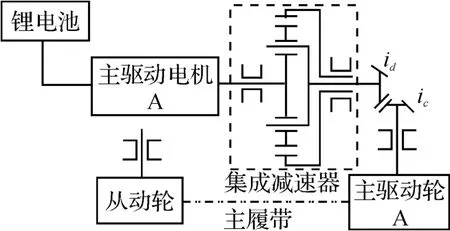
图2 机器人主驱动系统原理图

2．2 机器人传动比的计算

2．2．1 传动系最小减速比计算

机器人的最小减速比应由机器人行驶的最大速度及电机额定转速共同决定。机器人的行驶速度、系统的传动比如式(1～2)所示:

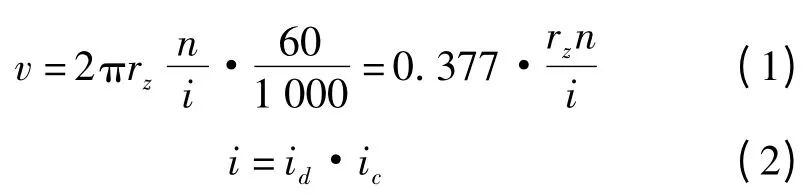
由式(1～2)得:

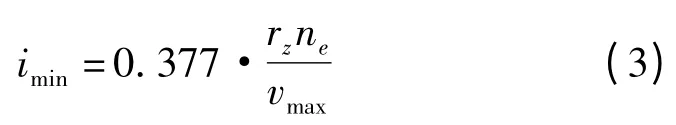
式中:v—机器人运动速度，km/s;n—驱动电机的转速，r/min;ne—电机额定转速，r/min;i—传动比;rz—车轮外半径，m。

设计采用BG 系列永磁无刷电机，额定转速:ne=37 000 r/min;采用6 英寸山地车车轮作为轮系机构，外径:rz=0．152 4 m。

由vmax=1．6 m/s(5．76 km/h)，ne=3 700 r/min，rz=6(0．152 4 m)代入式(3)得:

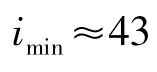
2．2．2 传动系最大减速比计算

机器人的最大减速比应由机器人行走时最小速度和电机额定转速共同决定。根据电机外特性，机器人在低速爬坡时，应以峰值转矩来计算传动比。若将nfp=ne代入式(3)计算，则会产生较大误差。所以，研究者应该用电机恒转矩区间内的特性来计算其在最低速稳定爬坡时的调速比，使机器人能够在设定的αmax=30°坡度上稳定爬坡，则其需要的牵引力为:

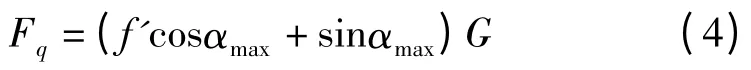
将式(4)代入式(3)，得:

式中:Tmax—电动机峰值转矩，N·m。

由电机外特性，选择恒功率临界点的速度nh=n，代入式(1)，得:

将vmin=0．5 m/s，vmax=1．6 m/s，imin=43 代入式(6)，得:

imax=137

2．3 机器人动力系统功率的计算

2．3．1 机器人额定功率计算

机器人在正常路面上行驶达到最大速度时，其所需功率即为最大额定功率，其计算公式如下:

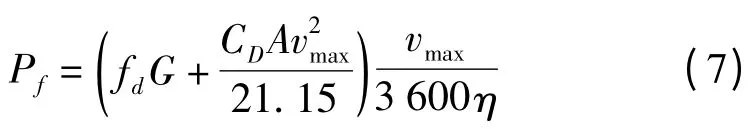
式中:Pf—机器人在正常路面高速行驶时的最大功率，kW;G—机器人自重，N;CD—风阻系数;vmax—机器人最高行驶速度，km/s;fd—机器人在正常路面上行驶时的摩擦系数;η—机器人的机械效率。

由于机器人运行速度相对不高，为简化计算而忽略风阻系数影响，即只考虑理想状态下在正常道路上稳定行驶时的额定功率。则式(7)可简约为:

式中:fd—摩擦系数，fd=sinα +f'cosα。若在正常路面上行驶，其坡度较小，故:cosα≈1，sin≈γ，则:

式中:f'—滚动摩擦系数，f' =0．03～0．04;γ—道路坡度，坡高与坡水平的距离之比，γ－0．025;fd=0．055～0．065。

机器人的机械效率由3 部分组成，如公式(10)所示:

式中:ηd—动力装置机械效率，ηd=0．80～0．95;ηch—传动装置机械效率，ηch=0．80～0．90;ηx—行驶装置的机械效率，ηx=0．85～0．90。

由于高速时，η 损失有所增加，η 应取较低值，即:η=0．578。

由设计任务要求机器人的标准配置:重量G =1 800 N，vmax=1．6 m/s(5．76 km/h)代入式(8)得:

Pf≈0．274 kW

为保障机器人完全具有带G=600 N 负载能力，防止过载而损坏，取安全系数K =2，机器人需要的额定总功率为:

Pe=2 ×0．274≈0．548 kW

2．3．2 机器人电机最大转矩计算

机器人主驱动电机最大转矩的选取，应满足爬坡和骁原地中心转向为目标的需要，计算公式如下式所示:

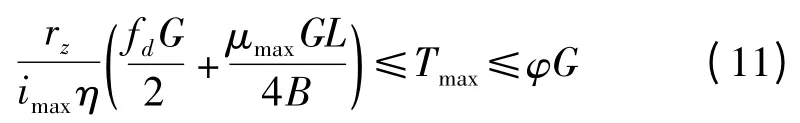
式中:Tmax—电机最大转矩，N·m;imax—最大传动速比;imin—最小传动速比;φ—履带与地面附着系数;rz—车轮半径，m。

由设计任务要求取:G =1 800 N，rz=0．152 4 m，vmax=1．8 km/h，μmax=1，imax=137，imin=43，fd=0．55～0．65，L=0．6 m，B=0．8 m，η =0．578，φ =0．4，代入式(11)，得:

0．867 5 N·m≤Tmax≤5．14 N·m

3 排爆机器人运动机构仿真

通过机器人运动机构参数计算可知，最大转矩靠锥齿传动轴传递到车轮，是关键主零件。下面以锥齿传动轴为例，论述有限元分析技术的应用。

该部件主要用于传递主驱动电机转矩到外行驶轮，分析件在组装图中的位置如图3 所示，是运动系统的关键部件。为了保证平台在运行过程中的可靠性，需要知道分析件工作中的最大变形量和最大应力值，再与其所用材料的许用值进行比较，得出分析部件的安全系数和安全度结论［7］。所以，这里借助有限元分析技术对该传动轴进行数值仿真模拟的建立和计算。

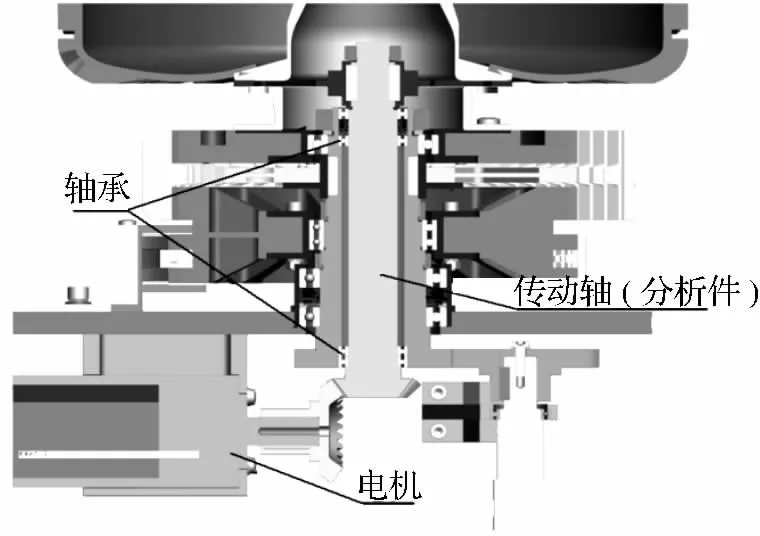
图3 分析件在组装图中的位置

不同的分析目的对于CAD 模型的要求不同。在建立有限元模型时，如果只关注结构整体，则可以将结构的细小特征压缩。例如，要分析结构整体模态，则可去除小的圆角、倒角和螺栓孔等。这就需要在简化模型时本着抓住主要矛盾、忽略次要矛盾的理念，对不影响整个模型受力的细小结构和影响生成高质量网格的结构进行简化和去除，保留主要结构，忽略次要结构［8］。

该零件选用45 号钢，其材料特性如表1 所示。

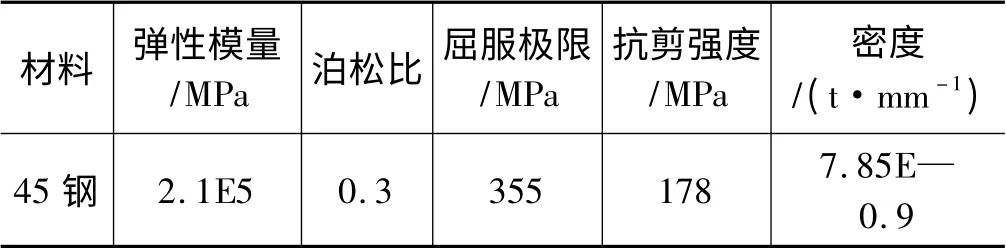
表1 选用材料属性

综合考虑模型最小几何特征和网格数目等因素，本研究将平均网格尺寸设置为1 mm，选用8 节点六面体单元SOLID185，总共得到161 358 个节点和153 812 个单元。

根据已知约束和载荷条件，本研究在有限元模型上添加对应位置的约束和载荷如图4 所示。

考虑该传动轴在电机启动的瞬间的应力值和变形量会是最大，此时的模型边界条件包含:

(1)约束条件。阶梯轴与固定轴承连接部分约束径向和轴向移动，以及绕径向和切向的转动，键槽部分约束切向移动和轴向的转动;

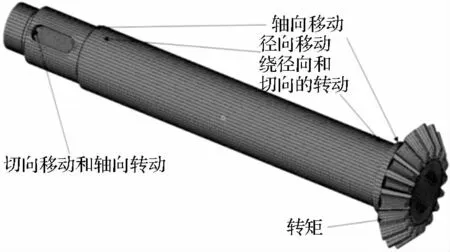
图4 边界条件施加位置

(2)载荷。考虑到齿轮传动中两对齿啮合和一对齿啮合两种情况，选用电机启动的瞬间只有一对齿啮合的特殊情况，施加转矩(考虑将转矩转化为力施加在单齿的切向方向上)为:

Tc=T×i×n=1 160 N·mm×42×18/22×0．81=32 288 N·mm

本研究将建立好得到的有限元模型导入大型有限元分析软件ANSYS 中，可得到模型的变形量和应力计算结果，其变形云图和应力值如图5 所示。

图5 轴模型有限元分析计算的变形、应力云图

由图5 可以看出，该部件最大变形量为0．064 mm，主要分布在锥齿轮部位;该部件最大应力为132 MPa，分布在模型的轴向固定槽处。

由上述计算结果可知，该模型的最大应力为132 MPa，小于该零件材料的屈服强度355 MPa。其安全系数为n=355/128 =2．7。通过应力云图可以看出分析件在轴向固定槽出现应力较大，其他大部分区域的应力值都很小，所以该零件在该种工况下足以满足其强度要求。

4 机器人运动机构的测试

历时近一年时间，目前本研究已完成排爆机器人运动机构的组装调试工作，并对机构进行以下测试:

(1)正常路面行驶速度的测试。在混凝土路面，负重60 kg，全速运行;激光测速仪测得速度v=1．61 m/s。

(2)爬楼梯测试。楼梯台阶高150 mm、间距300 mm，每层有14 个台阶，中间有转弯平台分隔，共用时t=11．8 s，测试现场如图6 所示。

(3)爬斜坡测试。斜坡倾角35°，从底部爬到顶部共用时约t =8 s。在斜坡任意位置可以暂停后重新启动。

(4)跨越障碍物测试。用大石块堆砌一道高250 mm、宽250 mm 的石槛，机构用时约t =5 s，顺利跨越。

以上测试表明机器人运动机构完全符合设计要求。

图6 爬楼梯试验图

5 结束语

本研究从运动学角度出发，在轮履复合机构越障机理的基础上，推导出了动力系统的传动比、额定功率、最大转矩等参数的实用数值，并运用有限元分析技术优化了传动系统主要部件的参数设计，提高了部件与整体系统的可靠性与安全性。最后对运动机构的运动性能进行了实地验证，为今后进一步改进设计提供了宝贵经验。

该排爆机器人运动机构尚未在复杂环境下进行严格测试，实际环境比本研究的试验环境要更复杂，对运动机构的性能将提出更高要求，这是下一步将要继续研究的方向。

［1］陈 波，李晓楠，王 进． 警用机器人一览［J］． 轻兵器，2005(6):28-29．

［2］王越超．我国危险作业机器人研究开发取得新进展［J］．机器人技术与应用，2005(6):11-18．

［3］曹其新，张 蕾．轮式自主移动机器人［M］．上海:上海交通大学出版社，2012．

［4］陈淑艳，陈文家．履带式移动机器人研究综述［J］．机电工程，2007，24(12):109-112．

［5］KIM J H，LEE C G． Variable transformation shapes of single-tracked mechanism for a rescue robot［C］//Proceedings of the 2007 IEEE International Conference on Control，Automation and Systems． Seoul:IEEE，2007:1057-1061．

［6］ROHMER E，YOSHIDA T，OHNO K，et al． Quince:A Collaborative Mobile Robotic Platform for Rescue Robots Research and Development［C］// The 5thInternational Conference on the Advanced Mechatronics． Tokyo:Japan Society of Mechanical Engineers，2010:225-230．

［7］张志文，等．机械结构有限元分析［M］．哈尔滨:哈尔滨工业大学出版社，2002．

［8］赵汝嘉，曹 岩．机械结构有限元分析及应用软件［M］．北京:高等教育出版社，2012．