线性二次调节器在机械臂非线性控制中的应用研究*

魏 来，贠 超 ，杨学兵

(北京航空航天大学机械工程及自动化学院，北京100191)

0 引 言

在工业生产线上，工业机械臂的应用可以提高工作效率，保证产品的稳定性，并改善工人的工作条件，因此，目前工业机械臂已经被广泛地应用在自动化生产过程中。为了满足自动化生产中更加精细的作业需求，如何提高机械臂的控制精度成为当今该领域的研究热点之一。针对轨迹型机械臂，例如焊接机器人，对如何提高其轨迹精度进行研究是重点之一。

机械臂是一个非线性的时变系统，在非线性控制理论中，计算力矩法［1-2］是一种比较适用于机械操作臂的控制方案。通过这种方法建立的控制器能够抑制扰动，并能保证机械臂在任何姿态下都能够跟踪目标轨迹。通过建立机械臂的动力学方程，机械臂系统被解耦和线性化，最终各个关节表现为独立的二阶系统。实现这种控制方法的前提是能够建立足够精确的动力学模型，然而在实际中很难做到这一点，例如，难以确定摩擦模型的结构。此外，随着机器人老化，动力学参数会变得不具有重复性，而且当机械臂抓持不同工具或工件时，工具或工件的惯量也会改变机械臂的动力学特性。

有缺陷的动力学模型会造成机械臂的伺服误差，导致控制精度下降。针对这一问题的研究，已经有部分学者取得了一定的成果。

文献［3］应用了一种自适应方法，并证明了这种方法的全局稳定性。这种方法依据机械臂的状态和伺服误差，系统调整动力学模型中的参数值，学习系统本身的动力学特性。随着人工智能技术的发展，后续的研究中人工神经网络和模糊控制［4-8］等技术被逐渐应用在机械臂控制技术中，以减小有缺陷模型带来的影响。Miyamoto［9］将反馈误差学习神经网络用在机械臂轨迹控制中。文献［10］中，设计了一个鲁棒模糊控制器用来稳定一类可解的非线性广义系统，这种方法对于机械臂适用。文献［11-13］将模糊PID 控制器应用到机械臂上。这些方法都能够在没有精确模型和参数的条件下处理高度复杂的动态系统。

线性二次型(LQR)易于实现且具有工程性，计算和实现更为容易［14］，已被广泛运用在工程中，运用线性二次调节器［15-16］，通过收集先前动作中的伺服误差信息生成误差修正项，消除动力学模型不精确引起的伺服误差。整个学习型控制器保持了原有基于动力学模型的非线性控制器结构，经过反复训练，通过提高机械臂关节空间的运动精度，达到提高轨迹精度的目的。该方法适用于做重复性工作的机械臂，当其需要完成新的任务时，之前的学习经验将失去作用。

笔者的研究过程包括一个两关节机械臂的仿真过程，以及在实验平台上的实验结果，经验证该方法能够起到抑制伺服误差、提高轨迹精度的作用。

1 机械臂控制器

具有学习功能的控制器是在基于动力学模型的非线性控制方法的基础上实现的。

机械臂动力学方程可以表述为如下形式:

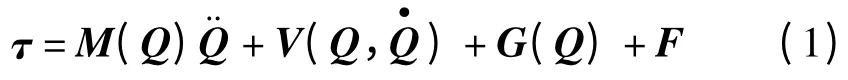
式中:τ—n ×1 的关节力或力矩组成的矢量;Q—n ×1的关节当前位置矢量;M(Q)—机械臂的n ×n 惯量矩阵;V(Q，)—n×1 的离心力和科氏力矢量;G(Q)—n×1 的重力矢量;F—n×1 的摩擦力矢量;n—机器人的自由度数［17］。

当本研究控制机械臂时，基于模型参数建立的动力学方程为:

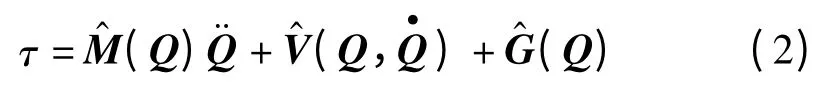
由于很难建立正确的摩擦模型，一般的控制器不包含摩擦模型。

采用线性化解耦控制律，令:

其中:

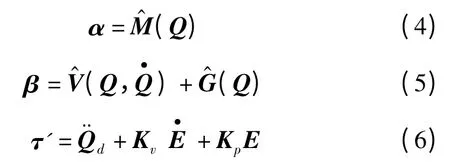
式中:Qd—n×1 的关节目标位置矢量;E，—n ×1 维的位置误差和速度误差矢量;矩阵Kv，Kp—n ×n 的对角矩阵，对角线元素分别为表示为kvi和kpi。

E 的表达式为:

将式(1，3)联立，可得到系统的闭环特性的误差方程为:

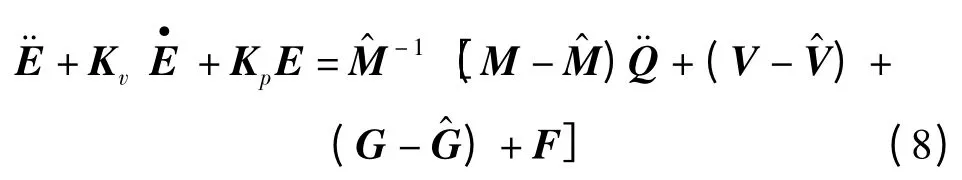
在基于模型的非线性控制方法中，通常将模型考虑为绝对精确，因此式(8)的右侧为零，此时闭环特性的误差方程变为:

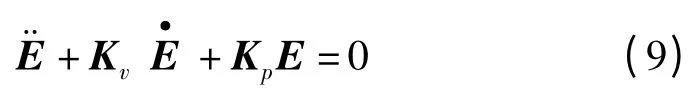
由于Kv和Kp是对角阵，此时机械臂可以被很好地解耦和线性化。式(9)可写成各关节独立的形式:

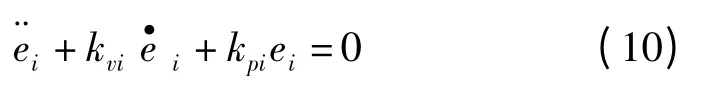
最终得到的控制系统如图1 所示。

光滑的目标轨迹是时间的连续函数，以关节角度Qd、角速度、角加速度矩阵的方式给出，整个系统可以准确地跟踪期望轨迹。

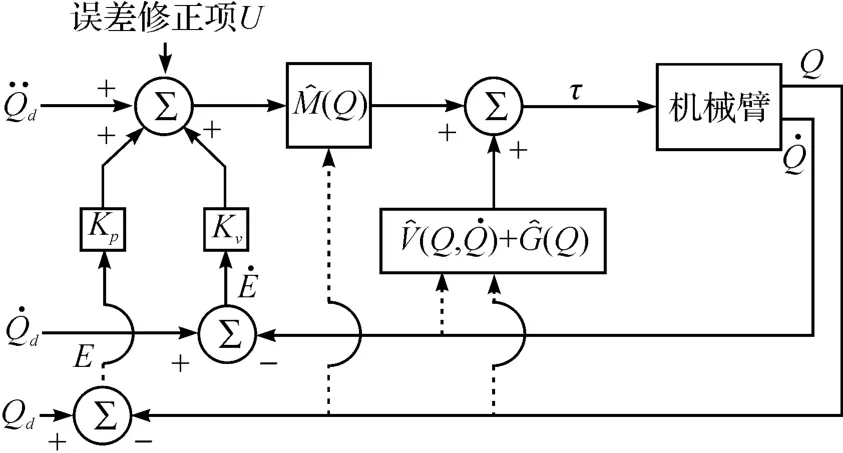
图1 基于模型的具有学习功能的机械臂控制器

上述便是基于模型的线性化解耦控制律，也称为计算力矩法。

然而通常情况下，精确的动力学模型很难得到。由于实际参数与模型参数的不一致，即式(8)右侧不为零，这将会引起伺服误差，甚至导致系统失稳。可以考虑在控制系统中增加一个误差修正项U，此时闭环特性的误差方程变为:

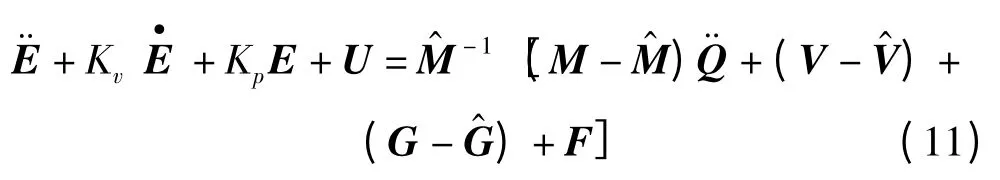
式中:误差修正项U—n ×1 的向量，形式为U =［u1，…，un］T。

如果修正项U 能够与式(8)右侧相等，便能补偿模型与实际的偏差，闭环特性的误差方程仍能保持为式(9)的形式，系统仍旧能够得到很好地解耦和线性化。

因此，如图1 所示，本研究要在控制系统设计时，引入线性二次调节器以生成误差修正项U。

2 线性二次调节器

机械臂的控制系统以一定的频率运行，机器人的各个关节的关节角度Qd、角速度、角加速度矩阵以离散点的形式以一定的频率发送。因此，误差补偿项U 也是离散发送的，可以将其考虑成离散时间决策的有限阶段马尔可夫决策过程模型。

模型包含4 个元素(S，A，Psa，R):

S—可能的状态集合，

A—可能的动作集合，

Psa—状态转移概率分布函数，

R—惩罚函数。

由于LQR 可以应用在有缺陷的模型中，只要调节次数足够多，仍能够起到理想的效果。LQR 的这一特性很好地解决了难以得到机械臂精确动力学方程的问题。

在有缺陷的模型中忽略模型误差，闭环特性的误差方程可表示为:

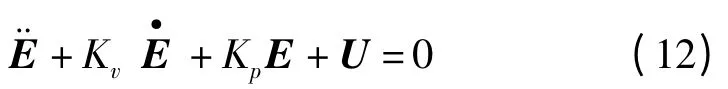
换成独立关节的形式，第i 个关节的误差方程为:

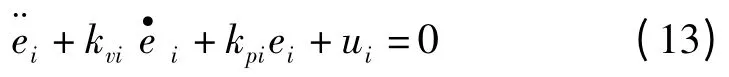
将该二阶系统设计为临界阻尼系统，即保证二阶系统的极点是两个相等的实根。此时，系统将以最短的时间运动到平衡位置而不出现震荡。因此，控制增益设定为:

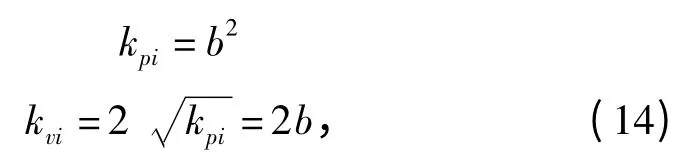
此时，微分方程(12)的通解为:

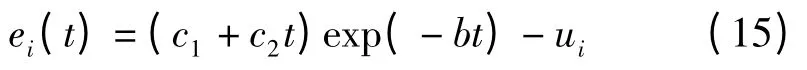
若初始条件为ei(0)和(0)，可得:

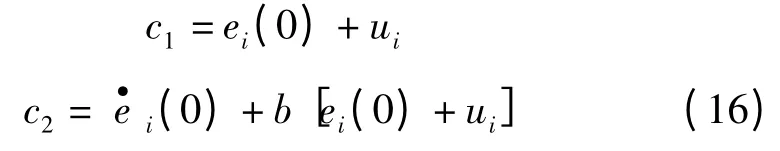
将式(16)代入式(15)，得到特解:

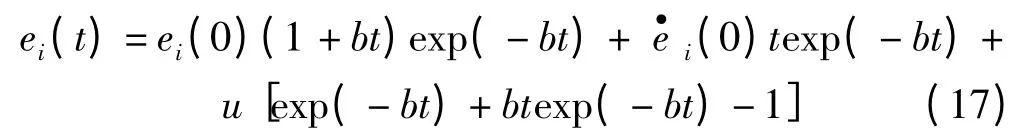
将式(17)对时间求导，可得:

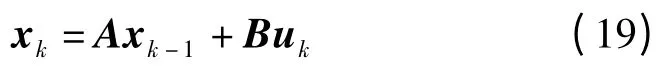
式中:

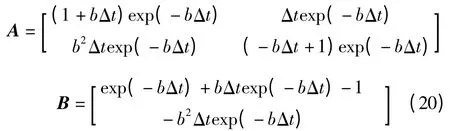
在b 和Δt 确定后矩阵A 和B 是常数矩阵，因此机械臂控制系统是一个离散的线性系统，且在当前状态xk-1和动作uk-1确定的条件下，下一时刻状态xk是确定的，即状态转移概率分布函数Psa=1。

利用LQR 产生最优控制策略，其中惩罚函数是状态xk和动作uk的函数，即:

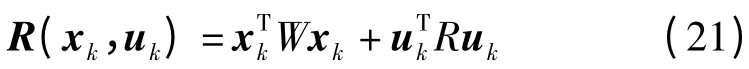
因此，机械臂单关节运动过程性能指标可以表示为:

通过运算求最优控制动作序列uk(k =1，…，N)，使性能指标最小。式(22)中可以起到抑制伺服误差的作用;另一项用来抑制动作幅度，以防止过度调节。

使性能指标最小的动作序列可以用下面的公式求得:

其中:

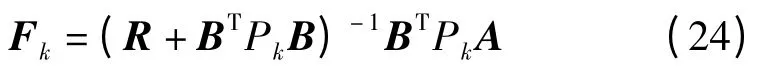
Pk可以通过逆向迭代的方式，用Riccati 方程［18］求得，即:

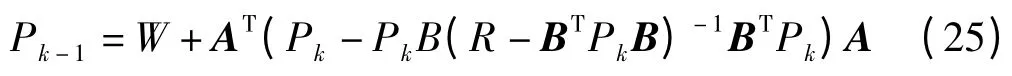
初始条件是:

线性二次型调节器对每个关节分开运算，通过提高每个关节的关节空间轨迹精度，以提高机械臂末端的轨迹精度。当机械臂重复同一动作时，每运行一次便可采集k 关节的伺服误差eik与ik，并生成一组误差修正项。

值得注意的是，新生成的误差修正项要累加到之前的误差修正项的和中，在下次运行时对模型误差做出修正。这样通过重复训练，整个机械臂可以逐渐接近于式(9)中理想的系统，直到伺服误差足够小时可以停止训练。

3 算例仿真

用ADAMS 软件进行仿真，建立一个简单的两个自由度(2DOF)机械臂。两自由度机械臂仿真如图2 所示。

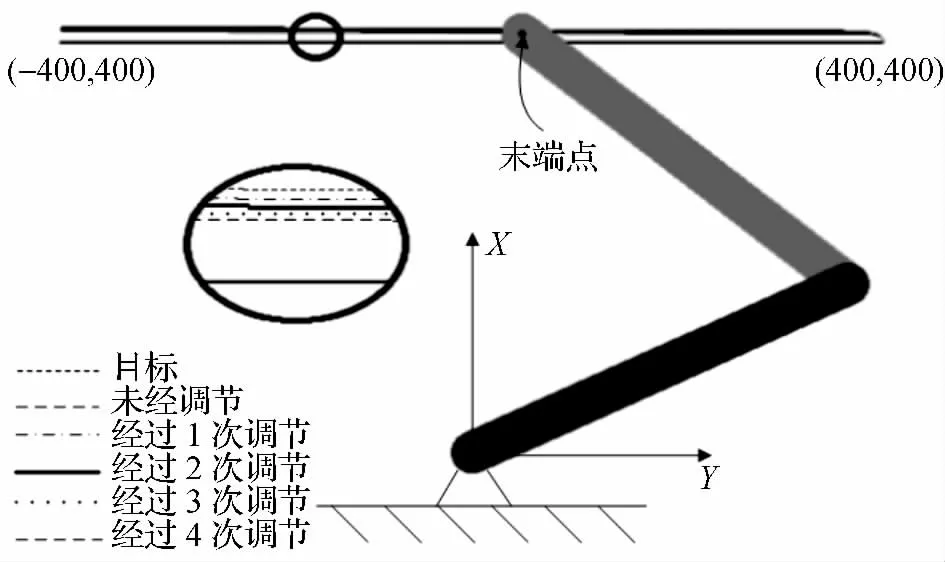
图2 两自由度机械臂仿真

两个连杆质量均匀分布且参数相同，均为:

长l=0．4 m，

宽0．04 m，

厚0．02 m，

质量m=2．693 kg，

转动惯量CI=4．2 ×10-2kg·m2，

控制增益设定为kpi=100，kvi=20。

为了验证控制算法对动力学模型误差的补偿，本研究设定有误差参数包括:将两杆质量设置为3 kg，转动惯量设置为CI=3．8 ×10-2kg·m2。

如图2 所示，控制机械臂末端从点(400，400)沿直线运动到(-400，400)，经过轨迹规划，关节角度、角速度、角加速度如图3 所示。

将该机械臂动力学方程表示为式(1)的形式，其中:

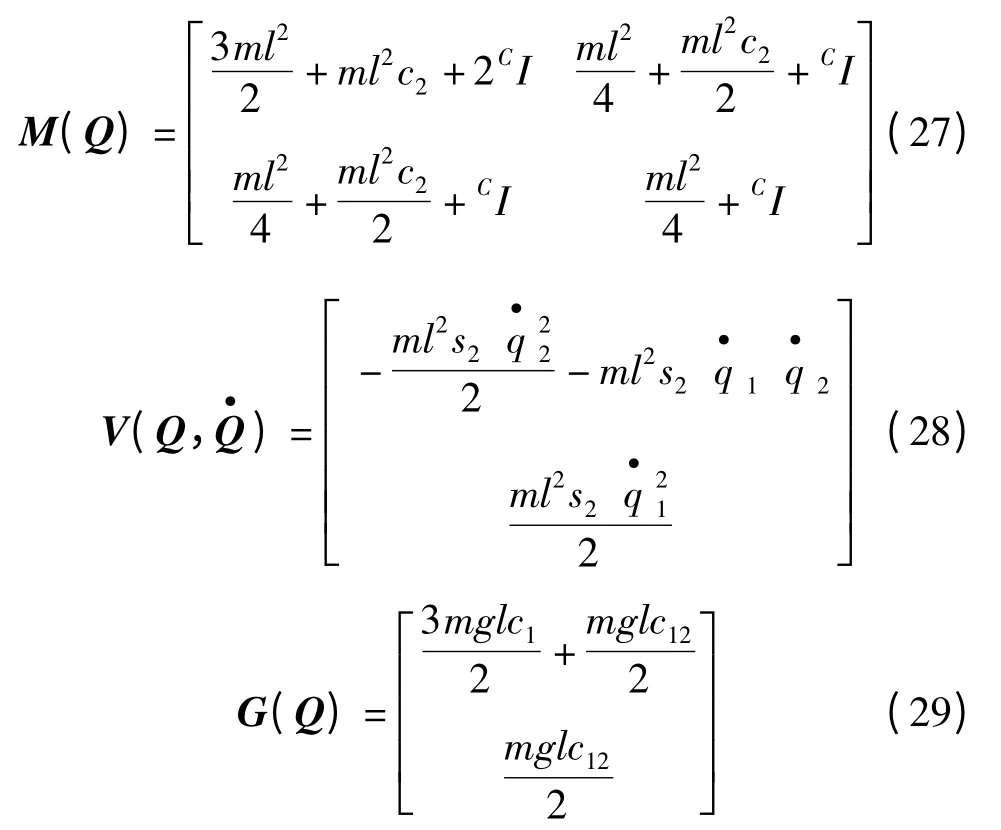
本研究建立如图1 中所示的控制系统，并进行多次运动仿真，并采集前一次运动过程中的速度与位置偏差在下次运行时进行误差修正。

ADAMS 动力学仿真结果如图2 所示，可以看出两自由度(2DOF)机械臂末端轨迹逐渐接近目标轨迹。这是由于经过四次调节，在关节空间实际运动轨迹与目标轨迹的角度偏差逐渐减小，使得机械臂末端在笛卡尔空间中的轨迹精度得到提高。

4 实验结果分析

实验平台如图4 所示。这是一个典型的机器人关节，由交流伺服电机通过同步齿形带驱动谐波减速器带动负载进行运动。

由于该算法分别针对单个关节进行调节，单关节实验平台可以用于验证算法的可行性。

图4 算法实验平台

本研究将关节角度目标轨迹设定为q =40·［1-cos(πt/3)］。关节角度轨迹误差随着调节次数增加的变化情况如图5 所示。

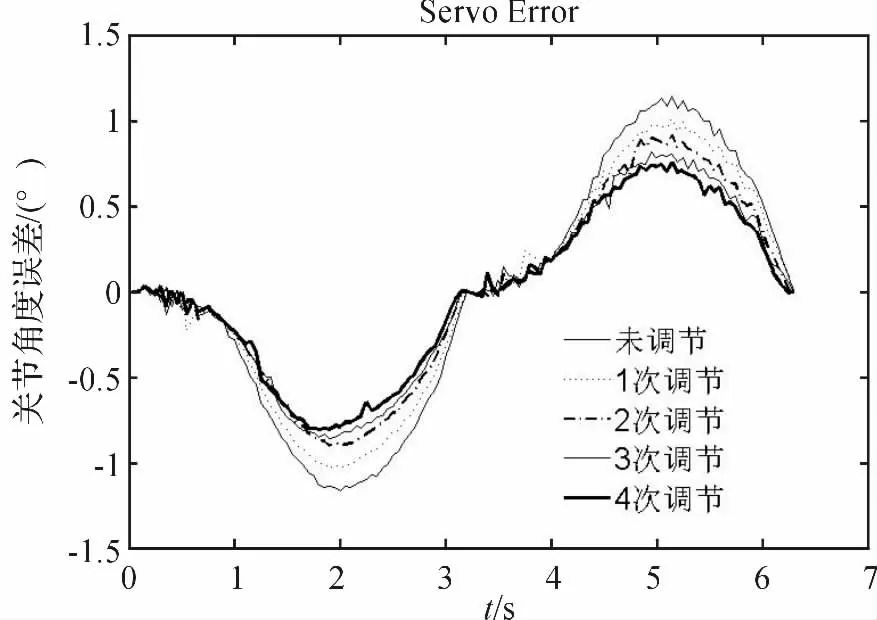
图5 伺服误差

最终得到的电机运动状态如图6 所示。整个过程电机速度较为接近标准的正弦曲线。参考图5 和图6可以看到，当正向运动时伺服误差为负，反向运动时伺服误差为正。经分析，该误差是由于在动力学模型中忽略了摩擦想所致。

调解中的关节角度误差如表1 所示。

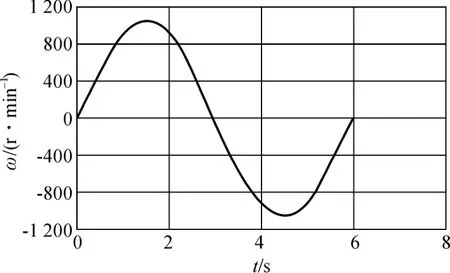
图6 电机运动状态

由图5 和表1 可知，经过了4 次调节，由于动力学模型偏差被逐渐补偿了，伺服误差大约减小了1/3，轨迹精度逐渐提高。实验结果很好地证明了该方法能够提高机械臂的运动精度。

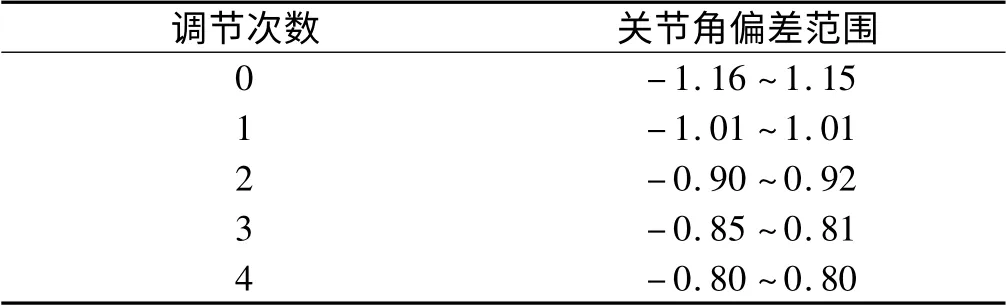
表1 调解过程中的关节角度误差

5 结束语

本研究提供了一种补偿机械臂动力学模型误差的方法，将误差修正项的确定归纳为有限阶段马尔可夫决策过程模型，并利用线性二次调节器(LQR)确定了最优的控制方案。该方法适用于机械臂的计算力矩控制法，能够有效地提高机械臂关节空间的轨迹精度，可应用于做重复工作的机械臂中。但是，该方法对于经常执行新任务的机械臂不适用。

本研究经过对两自由度机械臂仿真以及在机械臂单关节实验平台上的实验，验证了该方法的可行性。实验结果显示，伺服误差的减小速度很快。

［1］PAUL R． Modelling，trajectory calculation and servoing of a computer controlled arm［R］． STANFORD UNIV CA DEPT OF COMPUTER SCIENCE，1972．

［2］CRAIG J J． 机器人学导论［M］． Beijing:China Machine Press，2005．

［3］CRAIG J J，HSU P，SASTRY S S． Adaptive control of mechanical manipulators［J］． The International Journal of Robotics Research，1987，6(2):16-28．

［4］MURPHY R． Introduction to AI robotics［M］． Massachusetts:MIT press，2000．

［5］HAYKIN S S． Neural networks and learning machines［M］．Upper Saddle River:Pearson Education，2009．

［6］WAKILEH B A M，GILL K F． Use of fuzzy logic in robotics［J］． Computers in Industry，1988，10(1):35-46．

［7］KOSKO B． Neural Networks and Fuzzy Systems:A Dynamical Systems Approach to Machine Intelligence/Book and Disk［M］．Upper Saddle River:Prentice hall，1992．

［8］KARAKASOGLU A，SUDHARSANAN S I，SUNDARESHAN M K． Identification and decentralized adaptive control using dynamical neural networks with application to robotic manipulators［J］． Neural Networks，IEEE Transactions on，1993，4(6):919-930．

［9］MIYAMOTO H，KAWATO M，SETOYAMA T，et al． Feedback-error-learning neural network for trajectory control of a robotic manipulator［J］． Neural Networks，1988，1(3):251-265．

［10］WANG Y，SUN Z Q，SUN F C． Robust fuzzy control of a class of nonlinear descriptor systems with time-varying delay［J］． International Journal of Control Automation and Systems，2004(2):76-82．

［11］PRECUP R E，HELLENDOORN H． A survey on industrial applications of fuzzy control［J］． Computers in Industry，2011，62(3):213-226．

［12］BINGÜL Z，KARAHAN O． A fuzzy logic controller tuned with PSO for 2 DOF robot trajectory control［J］． Expert Systems with Applications，2011，38(1):1017-1031．

［13］PILTAN F，SULAIMAN N，ZARGARI A，et al． Design PID-like fuzzy controller with minimum rule base and mathematical proposed on-line tunable gain:applied to robot manipulator［J］． International Journal of Artificial intelligence and expert system，2011，2(4):184-195．

［14］胡寿松，王执铨，胡维礼．最优控制理论与系统［M］．上海:上海科学出版社，2005．

［15］SCOKAERT P O M，RAWLINGS J B． Constrained linear quadratic regulation［J］． Automatic Control，IEEE Transactions on，1998，43(8):1163-1169．

［16］TEDRAKE R，MANCHESTER I R，TOBENKIN M，et al．LQR-trees:Feedback motion planning via sums-of-squares verification［J］． The International Journal of Robotics Research，2010(29):1038-1052．

［17］BEMPORAD A，MORARI M，DUD V，et al． The explicit linear quadratic regulator for constrained systems［J］． Automatica，2002，38(1):3-20．

［18］白丽平．基于ADAMS 的机器人动力学仿真分析［J］．机电工程，2007，24(7):74-77．