R语言统计建模方法在满意度预测中的应用

中博信息技术研究院有限公司 魏利明 陈文冬

R语言统计建模方法在满意度预测中的应用

中博信息技术研究院有限公司 魏利明 陈文冬

R语言是一套完整的用于统计分析和制图的开源软件环境，并逐渐成为统计建模的重要工具之一。阐述了统计建模的基本步骤，及其相应的R语言处理方法与技巧，并以用户满意度预测为案例，探讨R语言在统计建模上的具体应用。

R语言；统计建模；用户满意度预测

1 R语言简介

R语言是一套完整的用于统计分析和制图的开源软件环境，由新西兰奥克兰大学统计系的Ross Ihaka和Robert Gentleman共同创立的S语言演变而来。R语言具备以下特点：

1）它是一种高效的应用于数据处理与存储的代码语言；

2）它具备强大的数组运算功能；

3）它具备完整且连贯的统计分析函数；

4）它具有出色的统计制图功能；

5）基于开源的设计可以让用户自定义函数包，上传网络能够让全球用户共享使用；

6）丰富详实的帮助文档和开源免费的升级迭代服务大大提升了数据分析的效率，从而大大降低了软件升级的成本。

根据2014年IEEE Spectrum的最新调查，R语言在全球编程语言的综合排名中位列第七，在统计语言中位列第一，远远领先于SAS（统计分析软件）。R语言当前已覆盖Windows、Unix 和MacOS平台，成为全球最流行的统计分析语言之一。

2 R语言统计建模的步骤

一般而言，统计建模是以计算机统计分析软件为工具，利用各种统计分析方法对批量数据建立统计模型和探索处理的过程，用于揭示数据背后的因素，诠释社会经济现象，或对经济和社会发展做出预测或判断[1]。概括来说，统计建模应具备三个基本要素：数据、方法和工具。

R语言统计建模则是以R语言为分析工具，通过编写统计分析代码，对目标数据进行描述、解释，并通过建立模型提炼数据规律和规则，进而对未来趋势做出符合一定概率的预测或判断。具体来说，有如下几个步骤。

1）明确目标与确立假设。这是统计建模初期最基础也是最重要的工作。统计建模往往要面对海量纷繁复杂的数据，这意味着，在横向上，分析者往往要面对多维有时甚至几十维的观测向量；在纵向上，样本量的累积会大大增加数据的纵深。当观测向量维度众多、体量巨大时，整体数据集就会形成一个极为庞大的数据矩阵。此时就需要有明确的分析目标和分析需求，建立起必要的假设，凸显核心问题，才能有效指导下阶段的统计建模工作。否则，必然会使分析工作丧失目的和方向，削弱模型的应用价值，最终导致建模工作的结果南辕北辙。

2）数据获取与清洗。数据获取与清洗是统计建模的重要环节，通常占到整个数据工作60%～80%的工作量。

数据获取就是从一定的渠道按照假设体系的要求搜集建模所需要的数据信息，获取的数据叫做原始数据。R语言提供了从多种渠道获取数据的方法，例如：通常使用“download.file()”和“read.table()”函数用于获取网络数据；利用“read.csv()”、“read.xlsx()”可以读取csv和Excel数据；此外，加载XML（可扩展标记语言）包可以编写网络爬虫爬取网页信息；加载jsonlite包可以爬取jason格式数据；利用httr包并注册指定的API（应用程序接口）可以实现与API数据的对接；通过RMySQL（R语言程序包）可以与数据库对接获取数据。

数据清洗是指对原始数据进行异常值和缺失值的检验和处理，使得原始数据成为可用于统计建模的“结构化数据”。异常值主要包括离群值、高杠杆值和强影响值，当观测值大于三个标准差通常被定义为异常值。在R语言中，通过“outlierTest()”函数可以检查模型的异常值，“influencePlot()”函数能够返回异常值的交互图形，便于识别异常值。对于缺失值的处理可通过多重插补进行替换，或将缺失值删除。“sum(is.na())”函数以及“colSums(is.na())”函数是识别缺失值最常用的函数，此外，可以借助“aggr()”或“matrixplot()”函数返回缺失值分布的图形。

3）变量筛选与降维。如果说数据获取与清洗使得数据“可用于”统计建模，那么变量筛选与降维就是使得数据“好用于”统计建模的重要环节。一个清洗后的结构化数据往往还达不到直接建模的要求，或者说虽然可用于建模，但预测的效果往往并不理想，因为数据具有“维度灾难”（“curse of dimensionality”）的特性，即观测维度过多，导致样本在高维空间出现分布稀疏而难以确定判别的边界，降低预测效果。因此在正式建模之前必须要进行变量的选取。在R语言中，可以借助caret包的“varImp()”函数对变量重要性进行计算，选取影响力强的变量用于建模；此外，在处理大矩阵数据集时，可以借助“fa.varimax()”或“fa.promax()”函数进行主成分分析，对数据进行适度降维，其中前者使用正交旋转法，后者使用斜交旋转法。

4）模型训练、预测与测试。这是统计建模的核心环节，将对预处理后的数据进行建模。首先，根据数据类型选取合适的算法，不同的算法对数据的要求各不相同，例如，经典最小二乘回归要求特征值和标记值均为数值型变量；二元logistic回归要求标记值为二元分类变量；而随机森林（random Forest）模型，变量类型既可以是连续的，也可以是离散的。数据类型与算法高度匹配，建模时需格外注意。其次，将数据切分为训练集与测试集，通过构建交叉验证体系[2]，依次进行模型训练、预测和测试，重点观察测试集的预测误差，选取误差最低的模型。在R中，不同的算法有各自的建模函数，通常使用“predict()”命令拟合预测函数，交叉验证通过for()循环实现。

5）模型调试与优化。对于同一数据集，不同的模型会体现出不同的预测效果，一个好的模型应遵循“机理简单、稳健性好、适用性强、便于推广”的准则[3]，而根据“奥卡姆剃刀定律”（“Occam‘s razor”）：“如无必要，勿增实体”，则是说在模型解释力不变的情况下，首应选取更简洁的模型，而复杂的模型虽然具有较低的训练误差，但往往随着模型复杂度的增加测试误差逐渐上升，导致模型出现过度拟合，降低其泛华能力，削弱应用价值。在R语言中，模型调试的方法极为灵活，不同的算法均有相对应的调整参数，通常第一步是模型间比较，即通过比较选取预测准确率最高的基本模型；第二部是模型内调整，即在模型内部进行参数调优，使准确率得到进一步提升。

6）模型应用与部署。统计建模的目的不是创建一个好看的数学模型，而是要用于预测未来趋势，指导业务开展。因此，广义上的模型部署是指形成对未来趋势预测的平台和软件，以及一揽子政策建议、营销策略、工作标准等；狭义上的模型应用仅指对未来的预测。R语言的优势在于利用灵活的计算函数建立离线模型，而在模型部署上，还需要协同相应的产品经理、运维人员、软件开发和测试等部门的技术人员，以及掌握Linux，Java，Hadoop，Spark等技术。因此，鉴于模型部署较高的技术门槛，在企业内部部署模型，需要多个部门多种人才的协同。

3 手机用户满意度预测模型

本文以某省运营商手机用户数据和满意度调研数据为数据源，借助R语言建立满意度预测模型，探讨R语言在统计建模上的具体应用。具体实现步骤如下：

1）建模目标与假设。本案建模的目标是构建手机用户的满意度预测模型，要求模型能够预测识别“满意用户”（7～10分）、“一般不满用户”（4～6分）和“极端不满用户”（1～3分）。基本假设为：用户的手机使用行为和人口属性对其满意度存在显著性影响，以用户客观数据为特征值，满意度为标记值构建预测模型，预测提前量为3个月。

2）数据获取与清洗。用户满意度由1～10分李克特量表回访所得，样本量5 000粒，按该省运营商手机用户在各地市用户规模的比例随机抽样。用户客观数据包括人口属性和手机使用行为数据，人口属性为用户性别和年龄，使用行为以3个月前的数值为统计时间点，包括：用户累计入网月数，是否更换套餐，当前套餐使用月数，会员等级，月租费用，月ARPU（每用户平均收入）值，月流量，月总通话时长，月短信数量，客观数据由运营商数据库提取。将满意度数据与客观数据进行一对一匹配，形成结构化数据集，删除缺失值，主要代码如下（“#”后为代码解释）：

df＜-read.csv(file=“whole.province.csv”,header = T) # 读取数据

colSums(is.na(df)) # 查看缺失值在变量中的分布

df2 ＜-df[complete.cases(df),] # 删除缺失值

3）变量筛选与降维。对清洗后的数据集进行维度约减，保留强维度，去除弱维度，利用决策树算法和caret包进行变量筛选，主要代码如下：

fit.rpart＜- rpart(满意度～ ., data = df2, cp=0.001) # 决策树初步建模

plotcp(fit.rpart) # 绘制CP（复杂性参数）图见图1。

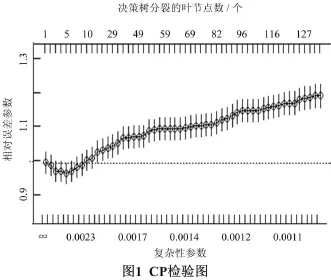
cptable$CP[which.min(cptable$xerror)] # 取误差值达到最小时的CP值

fit.rpart2＜-rpart(满意度～.,data=df2,cp=0.002831503) # 决策树二次建模

fit.Imp＜-varImp(fit.rpart2,scale=T,surrogates=F,competes=T) #自变量重要性计算

ggplot(fit.Imp,aes(x=name,y=Overall))+geom_bar(aes(fill=name), stat=“identity”)+coord_flip() # 自变量重要性直方图见图2。

4）模型训练、预测与测试。如前文所示，影响力较强的特征值依次是当前套餐使用月数、月短信、累计入网月数、月流量、年龄、月ARPU、均为数值型向量；标记值“满意度”为3分类变量。重新整合数据集，建立五折交叉验证，选取合适算法进行模型探索，以线性判别为例，经计算其训练集准确率为86.17%，测试集准确率为86.15%，主要代码如下：

5）模型调试与优化。本案适用的模型算法包括线性判别、随机森林、朴素贝叶斯、神经网络、支持向量机和自助整合等等，通过多种算法建模，汇总模型探索结果，如图3所示，在训练集准确率上，随机森林最高；在测试集准确率上，随机森林、支持向量机、线性判别均有不错的表现。具体模型效果表现见图3。

综合预测效果，选用随机森林进行进一步调试优化。引入建模参数importance计算自变量权重，引入proximity参数计算样本间近似值，引入ntrees参数并设置随机树为1 000棵，再次拟合模型，测试集准确率达到86.19%，较此前有所提升。主要代码如下：

6）模型应用与部署。至此R语言建模的工作已完成，接下来需要对模型进行软件开发和测试，嵌入运营商业务系统实施预测，实时了解用户未来3个月的满意度情况，以及不满用户的分布，并进行及时的关怀安抚工作。

4 小结

统计建模是一套完整的对数据进行获取、清洗、描述、解释，探索规律并最终做出预测的过程，它有着严谨的理论步骤，并依赖于专业的分析工具和方法。相对于其他统计分析工具，R语言在统计建模方面有着开源免费、处理灵活、函数功能健全等优势，但对编程和英语能力有较高的要求，同时在模型的部署上，技术门槛较高，需要协同多种技术背景和专业领域的人才共同参与实施。

[1] 米子川. 依数据进行统计建模的三个基本分析层次 [J]. 统计教育, 2010(10): 18-21.

[2] 吴喜之. 复杂数据统计方法——基于R的应用[M].北京：中国人民大学出版社, 2013: 33.

[3] 宋海燕, 曾宪福; 张立欣. 统计建模的探讨 [J]. 榆林学院学报, 2012(6): 29-31. ◆