非线性分数阶微分方程组奇异对偶系统正解存在性证明

张稳根，胡卫敏，刘 刚

（伊犁师范学院数学与统计学院，新疆 伊宁835000）

0 引言

近些年出现了很多关于分数阶微分方程及其应用的论文和专著［1－13］，其中大部分给出了一些特殊线性分数阶方程的可解性［3］.然而，D.Delbosco和L.Rodino在文献［4］中考虑了非线性分数阶微分方程Dsu＝f（t，u）的一个解的存在性（其中：0＜s＜1，f：［0，a］×R→R，0＜a＜＋∞为已知函数，且在（0，a）×R 上连续），应用Schauder不动点定理和Banach压缩映射原理得到了解的存在性.文献［5］用上下解方法考虑方程Dsu＝f（t，u）正解的存在性（其中：0＜s＜1，且f：［0，1］×［0，＋∞）→［0，＋∞）是已知的连续函数）.文献［6］分别用Krasnoselskii's不动点定理和锥上Leray－Schauder非线性抉择定理考虑奇异对偶系统

的正解存在性（其中：0＜s＜1；0＜p＜1；Ds，Dp为两个标准的Riemann－Liouville分数阶微分；f，ɡ：（0，1］×［0，＋∞）→［0，＋∞）是两个已知连续函数，且即f 和ɡ 在t＝0奇异）.本文分别用Krasnoselskii's不动点定理和锥上Leray－Schauder非线性抉择定理证明如下奇异对偶系统的正解存在性：

其中：0＜s＜1；0＜p＜1；Ds，Dp是两个标准的Riemann－Liouville分数阶微分；f，ɡ：（0，3］×［0，＋∞）→［0，＋∞）是两个已知连续函数，且

关于分数阶微分方程存在定理的发展和实际应用方程的情况参见文献［7］.文中涉及的分数阶积分和微分的定义及其相关基本性质，参见文献［8］或者文献［4］.

本文将用到的两个不动点定理.一个是Krasnoselskii's不动点定理；另一个是锥上Leray－Schauder非线性抉择定理.

引理1［1］设E 为一Banach空间，K⊂E 为E 上的一个锥.Ω1和Ω2是E 的开子集且连续且全连续.若下列条件之一成立：

（ⅰ）对于u∈K∩∂Ω1，有‖Au‖≤‖u‖；且对于u∈K∩∂Ω2，有‖Au‖≥‖u‖.

（ⅱ）对于u∈K∩∂Ω1，有‖Au‖≥‖u‖；且对于u∈K∩∂Ω2，有‖Au‖≤‖u‖.则A 在K∩上有一个不动点.

引理2［9］假设E 为一Banach空间，且C 是E 的闭凸子集.U 是C 的开子集且0∈U，A：→C 是连续的紧映射.那么如下结论至少有一个成立：

（2）存在u∈∂U 和λ∈（0，1）使得u＝λAu.

1 预备定理

记C［0，3］为所有定义在［0，3］上连续实函数组成的空间.令X＝C［0，3］×C［0，3］，其范数定义为

定义1［8］连续函数w：（0，3）→R 的0＜s＜1阶分数阶微分定义如下：

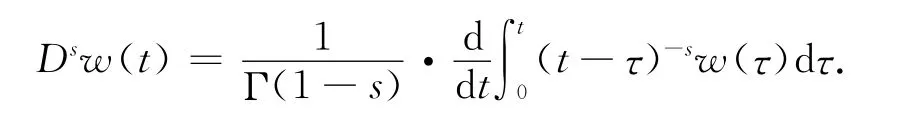
定义2［8］连续函数w：（0，3）→R 的0＜s＜1阶分数阶积分定义如下：

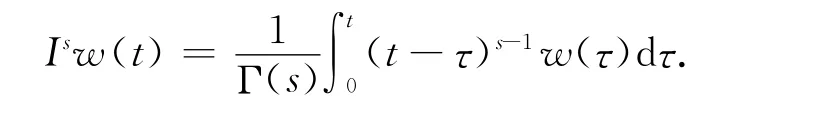
定义3［8］对于（u，v）∈X，s，p∈（0，1），连续分数阶导数Ds，Dp，如果

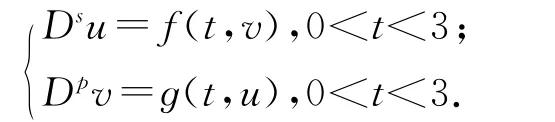
那么（u，v）是分数阶微分方程组对偶系统（1）的一个解.考虑如下积分方程对偶系统：

其中t∈（0，3）.

接下来证明，在某些条件下，方程组（1）等价于方程组（2）.首先，给出如下预备定理：

在［0，3］上连续.

证明 由tσF（t）的连续性和函数易知G（0）＝0.对于任何t0∈［0，3］，如果G（t）→G（t0）（t→t0，t∈［0，3］），则证明完成.为方便，证明分三种情形.

情形1 t0＝0，∀t0∈（0，3］.由于tσF（t）在［0，3］上连续，所以存在常数M＞0，使得｜tσF（t）｜≤M，t∈［0，3］.因此

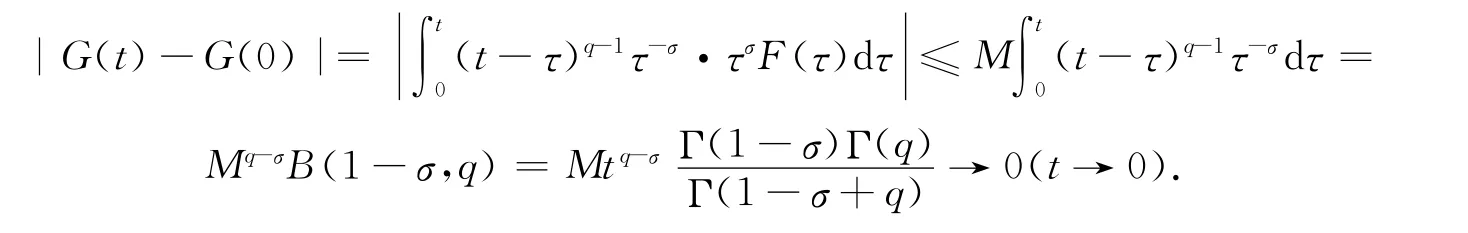
其中B 为Beta函数.

情形2 t0∈（0，3），∀t∈（t0，3］.

首先，有

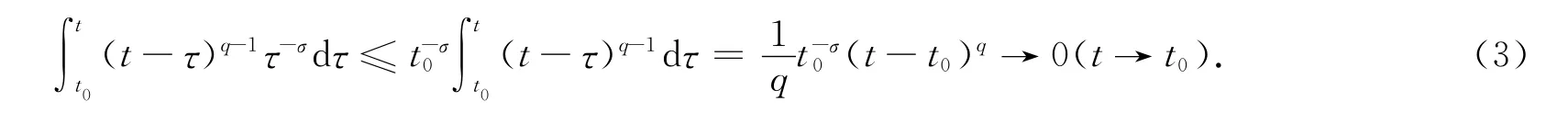
由（3）式可知

情形3 t0∈（0，3］，∀t∈［0，t0）时，证明类似情形2.省略.

定理2 假设0＜σ1＜s＜1，0＜σ2＜p＜1.f，ɡ：（0，3］×［0，＋∞）→［0，＋∞）连续，且连续.那么，方程组（1）等价于方程组（2）.

证明 ∀（u，v）∈X，由定理1可知Isf（t，v（t）），Ipɡ（t，u（t））∈C［0，3］.如果（u，v）∈X 是方程组（2）的一个解，那么∀t∈（0，3），有Dsu（t）＝DsIsf（t，v（t））＝f（t，v（t）），Dpv（t）＝DpIpɡ（t，u（t））＝ɡ（t，u（t）），即（u，v）是方程组（1）的一个解.

相反地，如果（u，v）∈X 是方程组（1）的一个解，则（u，v）∈X，且Dsu＝f（·，v（·））∈C（0，3］，Dpv＝ɡ（·，u（·））∈C（0，3］（C（0，3］表示所有定义在（0，3］上的连续实函数组成的空间，由文献［4］中命题2.4把R＋换成（0，3］得到），有IsDsu（t）＝u 和IpDpv（t）＝v.由于IsDsu（t）＝Isf（t，v（t））和IpDpv（t）＝Ipɡ（t，u（t）），因此∀t∈［0，3］有u（t）＝Isf（t，v（t）），v（t）＝Ipɡ（t，u（t）），即（u，v）是方程组（2）的一个解.

设K⊂X 为一个锥，定义

定义K 的子集

所考虑的正解（u，v）满足（u，v）∈D.

假设算子A：X→X，定义

即

定理3 假设0＜σ1＜s＜1，0＜σ2＜p＜1.f，ɡ：（0，3］×［0，＋∞）→［0，＋∞）连续而τσ1f（t，y）和τσ2ɡ（t，y）在［0，3］×［0，＋∞）上连续.则算子A：K→K 连续且全连续.

证明 ∀（u，v）∈K，有v∈K1＝｛y∈C［0，3］：y（t）≥0，0≤t≤3｝.由于

由定理1和f 的非负性可知A1：K1→K1.令v0∈K1，‖v0‖＝c0，如果v∈K1且‖v－v0‖＜1，那么‖v‖＜1＋c0∶＝c.由tσ1f（t，y）的连续性，知tσ1f（t，y）在［0，3］×［0，c］上一致连续.因此，∀ε＞0，存在δ＞0（δ＜1）使得∀x1，x2∈［0，c］，｜x1－x2｜＜δ时，有

显然，如果‖v－v0‖＜δ，那么∀t∈［0，3］有v0（t），v（t）∈［0，c］，｜v（t）－v0（t）｜＜δ.因此，∀t∈［0，3］，当v∈K1，‖v－v0‖＜δ时，有

由（7）式得

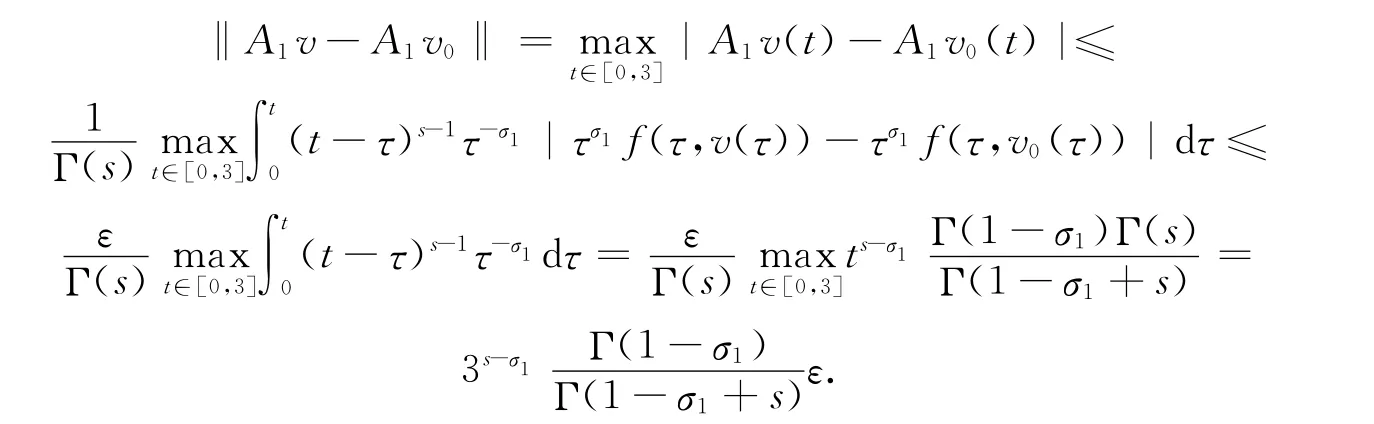
由v0的任意性可知A1：K1→K1连续.类似地，有A2：K1→K1也连续.即A：K→K 连续.

假设M⊂K 有界，即存在一个常数b＞0，使得‖v－v0‖＜b.由于tσ1f（t，y），tσ2ɡ（t，y）在［0，3］×［0，∞）上连续，令

∀（u，v）∈M，有

类似地，有

因此

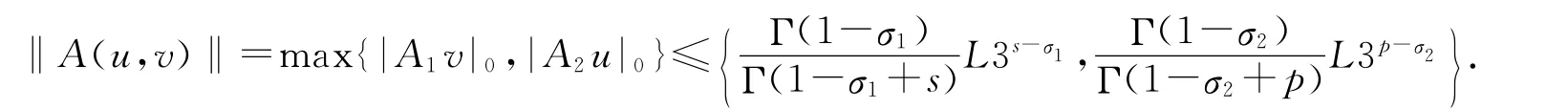
即A（M）有界.

∀ε＞0（ε＜min｛c1，c2｝），令δ＝min｛δ1，δ2｝，其中：

类似（4）式的证明，∀（u，v）∈M，t1，t2∈［0，3］，当t1＜t2时，有

现在证明：如果t1，t2∈［0，3］，且0＜t2－t1＜δ1，那么

（9）式的证明可分成如下三种情形：

情形1 t1＝0.由（8）式和t2＜δ1可知

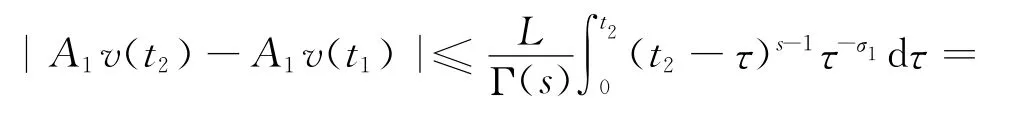
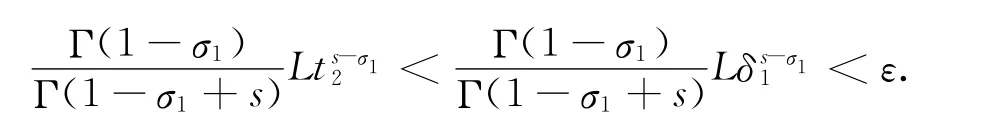
情形2 3＞t1≥δ1.由（8）式得

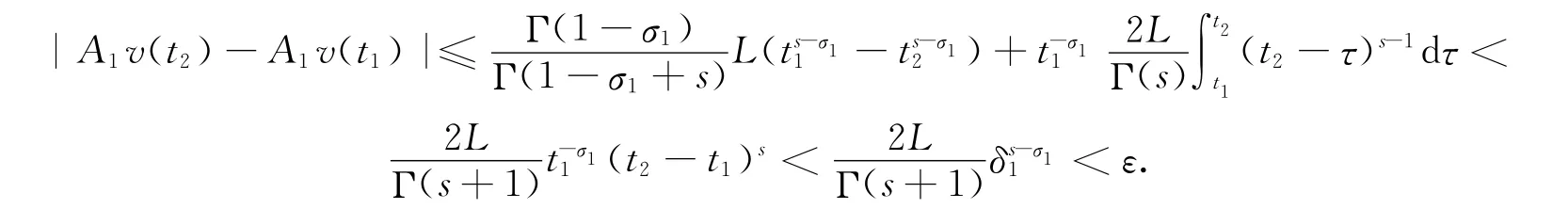
情形3 0＜t1＜δ1.由（8）式和t2＜2σ1可知

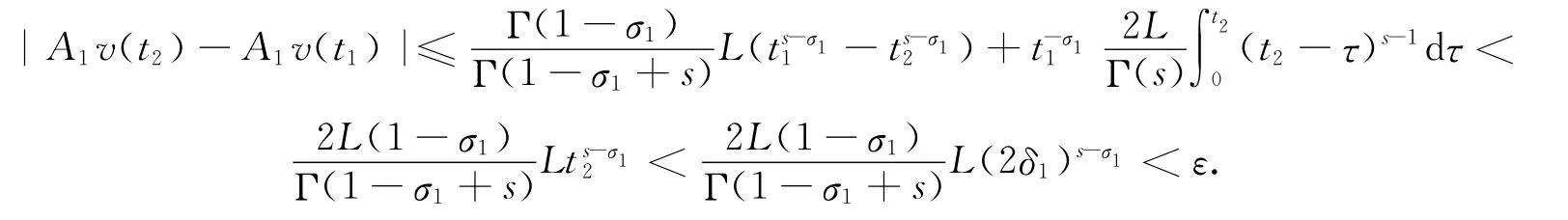
同理可证：如果t1，t2∈［0，3］，满足0＜t2－t1＜δ2，那么｜A2u（t2）－A2u（t1）｜＜ε.

因此，如果t1，t2∈［0，3］，满足0＜t2－t1＜δ，那么

因此，A 等度连续.由Arzela－Ascoli定理可知紧.所以算子A：K→K 全连续.

2 主要结果及其证明

定理4 假设0＜σ1＜s＜1，0＜σ2＜p＜1.f，ɡ：（0，3］×［0，＋∞）→［0，＋∞）连续，且在［0，3］×［0，＋∞）上连续.若存在两个独立的正常数ρ，μ，ρ＞μ，使得：

则方程组（1）至少有一个正解.

步骤1 假设Ω2＝｛（u，v）∈K：‖（u，v）‖≤ρ｝.对于（u，v）∈K∩∂Ω2，有0≤u（t），v（t）≤ρ，∀t∈［0，3］成立.由假设（H1）知，对于t∈［0，3］，有

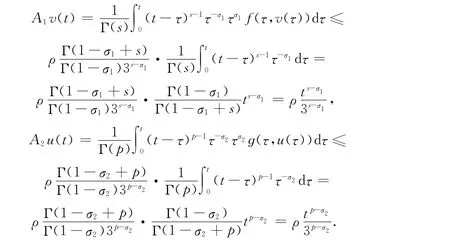
因此对于（u，v）∈K∩∂Ω2，有

步骤2 假设Ω1＝｛（u，v）∈K：‖（u，v）‖＜μ｝.对于（u，v）∈K∩∂Ω1，有0≤u（t），v（t）≤μ，∀t∈［0，3］成立.由假设（H2）知，

所以‖A（u，v）‖≥μ＝‖（u，v）‖对于（u，v）∈K∩∂Ω1成立.

因此，由引理1的（ⅱ）和定理2，证明完毕.

定理5 假设0＜σ1＜s＜1，0＜σ2＜p＜1.f，ɡ：（0，3］×［0，＋∞）→［0，＋∞）连续，且和tσ2ɡ（t，y）在［0，3］×［0，＋∞）上连续.若如下条件被满足：

（H3）存在两个增函数φ，ψ：［0，∞）×（0，∞），使得在［0，3］×［0，＋∞）上，有tσ1f（t，y）≤φ（w）和

（H4）存在r＞0，使得

则方程组（1）有一个正解.

证明 假设（u，v）∈K 为

的任一解，其中r∈（0，1），A 由（5）式给出.由定理3知A：K→K 连续且全连续.进而有A：K→D 和定理4中一样.由条件（H3）和（10）式可知，对于t∈［0，3］有

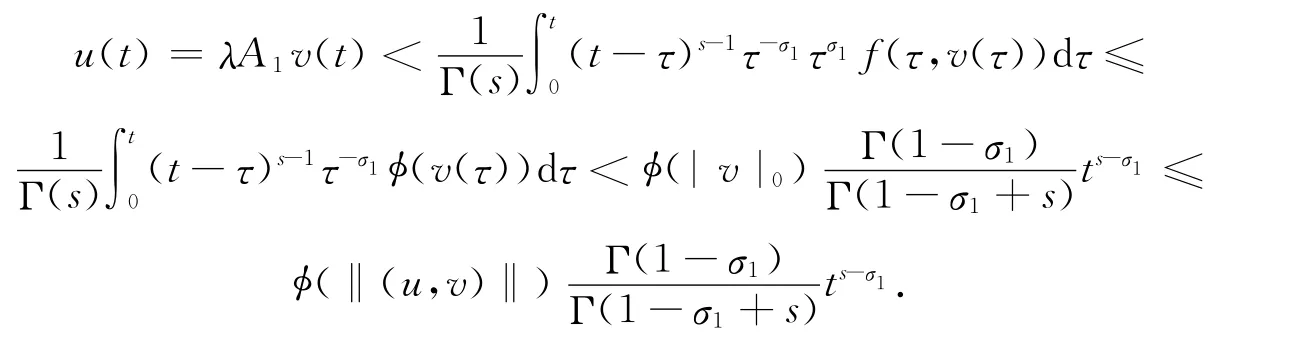
因此

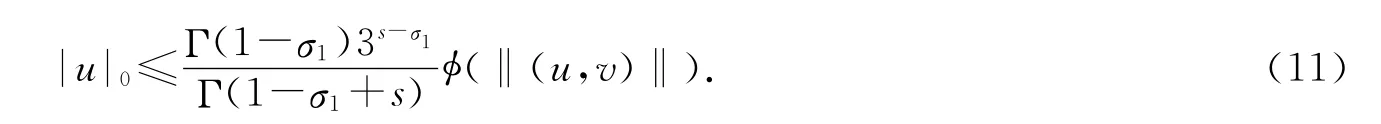
同理可得

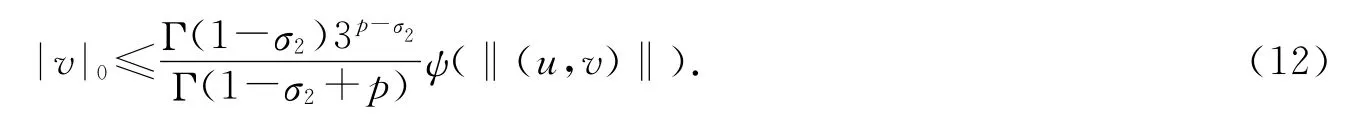
结合（11）和（12）式可得

由条件（H4）和（13）式可知‖（u，v）‖≠r.所以（10）式的任一解（u，v）满足‖（u，v）‖≠r.令U＝｛（u，v）∈K：‖（u，v）‖＜r｝.引理2保证了A 有一个不动点（u，v）∈¯U∩D.

由定理2可知，方程组（1）有一个正解.

例1 考虑分数阶微分方程对偶系统

其中0＜σ1＜s＜1，0＜σ2＜p＜1.则方程（14）有一个正解.

为了说明方程（14）有一个正解，可应用定理2，取

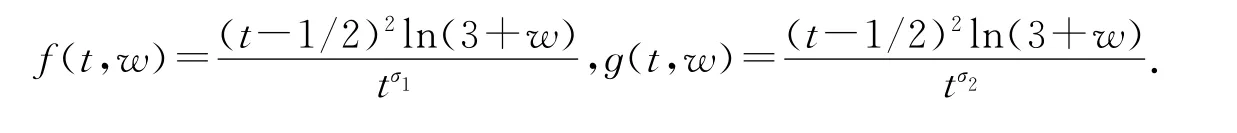
［1］KRASNOSELSKII M A.Positive solutions of operator equations［M］.Groningen：Noordhoff，1964：1－30.

［2］MILLER K S，KROSS B.An introduction to the fractional calculus and fractional differential equation［M］.New York：Wiley，1993：44－184.

［3］KILBAS A ANATOLY，SRIVASFAVA H HARI，TRUJILLO.Theory and applications of fractional differential equations［M］.Amsterdam：North－Holland Mathematics Studies，Elsevier Science BV，2006：56－90.

［4］DELBOSCO D，RODINO L.Existence and uniqueness for a nonlinear fractional differential equation［J］.J Math Anal Appl，1996，204：609－625.

［5］ZHANG S.The existence of a positive solution for a nonlinear fractional differential equation［J］.J Math Anal Appl，2000，252：804－812.

［6］BAI C Z.The existence of a positive solution for a ingular coupled system of nonlinear fractional differential equations［J］.Applied Mathematics and Computation，2004，150：611－621.

［7］KILBAS A A，TRUJILLO J J.Differential equations of fractional order：methods，results，and problems［J］.J Appl Anal，2001，78：153－192.

［8］SAMKO S G，KILBAS A A，MARICHEV O I.Fractional integrals and derivatives：theory and applications［M］.Switzerland：Gordon and Breach Science Publishers，1993：35－85.

［9］ZHAO G，SUN S R，HAN Z L，et al.The existence of multiple positive solutions for boundary value problems of nonlinear fractional diffusion equations［J］.Commun Nonlinear Sci Numer Simulat，2011，16：2086－2097.

［10］XU X J，JIANG D Q，YUAN C J.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation［J］.Nonlinear Analysis，2009，71：4676－4688.

［11］张丽娟，胡卫敏.一类Dirichlet型非线性分数阶微分方程边值问题的正解［J］.东北师大学报：自然科学版，2012，44（2）：39－43.

［12］刘刚，胡卫敏，张稳根.非线性分数阶微分方程边值问题的多重正解的存在性［J］.云南大学学报：自然科学版，2012，34（3）：258－264.

［13］许晓婕，胡卫敏.一个新的分数阶微分方程边值问题正解的存在性研究［J］.系统科学与数学，2012，32（5）：580－590.