混合双分数布朗运动下欧式期权的定价

徐 峰

(苏州市职业大学 商学院，江苏 苏州 215104)

混合双分数布朗运动下欧式期权的定价

徐 峰

(苏州市职业大学 商学院，江苏 苏州 215104)

提出一种新的不具有平稳增量的随机过程—混合双分数布朗运动，用来刻画标的资产的价格，进行欧式期权定价的研究.假设标的资产由混合双分数布朗运动驱动，运用对冲原理建立混合双分数布朗运动环境下的欧式期权价值所满足的偏微分方程，并采用边界条件和变量代换的方法得到该偏微分方程的解，即欧式期权的定价公式，其结果可看作是混合分数布朗运动和双分数布朗运动驱动下的一种推广.

混合双分数布朗运动；欧式期权；定价；长记忆性

传统的期权定价都是在假设标的资产服从几何布朗运动的基础上进行研究的，然而近年来大量的实证研究表明，金融资产的对数收益率并非服从正态分布，而是服从一种“尖峰厚尾”的分布，而且其价格之间也并非是随机游走的，存在着长记忆性和自相似性等分形特征，这导致了大量由布朗运动驱动的定价模型不符合真实的市场.分数布朗运动[1]已成为弥补上述模型缺陷最为简单的方法.

但是，文献[2]指出分数布朗运动不是半鞅，许多研究者用不同的方法给出了分数布朗运动的离散逼近，并指出直接将分数布朗运动应用于金融环境将会产生套利机会[3-4]，这使得分数布朗运动似乎不适合用于刻画金融资产价格变化的行为模式.从而，部分学者开始研究修正的分数布朗运动，如混合分数布朗运动、双分数布朗运动等[5-6]，由于双分数布朗运动不仅具有自相似性和长记忆性的特征，而且在一定的限制条件下是半鞅，因此可以应用于期权定价领域.

本文提出一种新的不具有平稳增量的随机过程—混合双分数布朗运动，用来刻画标的资产(如股票)的价格，进行欧式期权定价的研究.本文的结果可作为混合分数布朗运动和双分数布朗运动驱动下的一种推广.

1 预备知识

1.1 混合双分数布朗运动的定义与性质

定义1 如果满足均值为0，协方差为

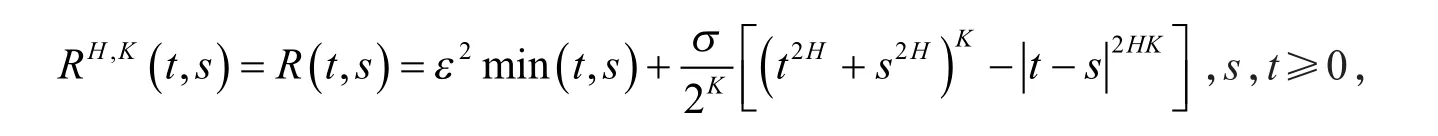
当K=1时，混合双分数布朗运动就退化成混合分数布朗运动；当时，混合双分数布朗运动就退化成双分数布朗运动.

由定义易知，混合双分数布朗运动具有以下性质.

性质1是HK-自相似的，即对任意α＞0，过程具有相同的分布；

性质2 当具有长记忆性；

性质3 当不是半鞅.

这些性质的证明可见参考文献[6].

1.2 模型假设

对金融市场做如下假设：市场无摩擦，即交易费用为零，无税收，不存在无风险套利机会；没有对交易头寸方向的限制，允许买空卖空证券；无风险利率r为常数；标的资产(如股票)的价格变化过程St服从过程

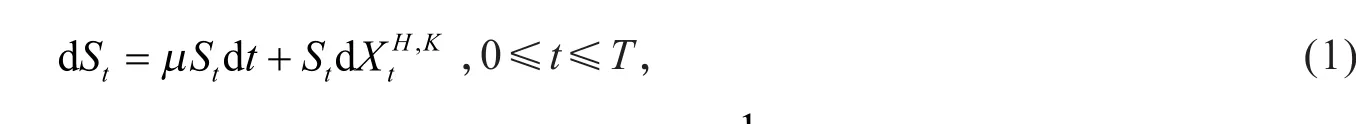
根据文献[7]易得到下面的引理.

引理1 随机微分方程(1)的解为

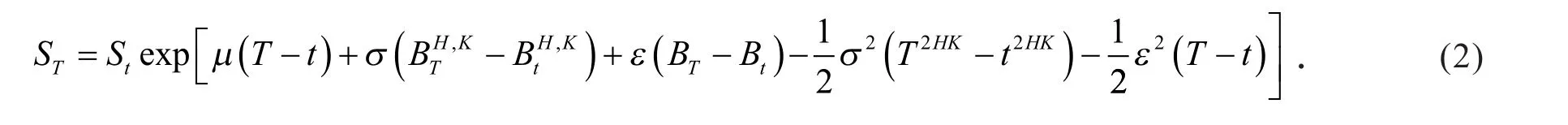
2 主要结果与证明

定理1 设Ct=C(t，St)是欧式看涨期权在t时刻的价格，股票价格满足方程(1)，则Ct满足偏微分方程

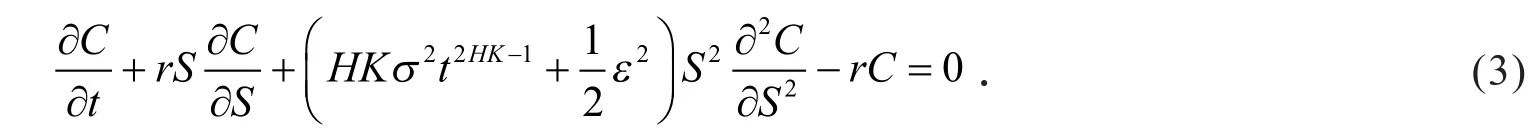
证明构建一个买入一份期权C和卖空Δ份股票S的资产组合Π，即Π=C-ΔS，则

选取适当的Δ使得资产组合Π在(t，t+dt)上是无风险的，即dΠ=rΠdt.令，则有

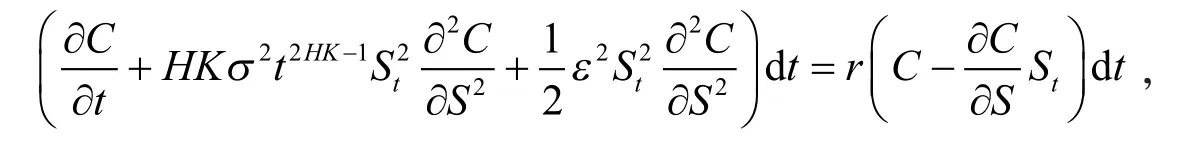
即有

定理2 假设到期日为T，履约价格为K，则混合双分数布朗运动下欧式看涨期权在任意时刻t∈ [0，T]的价格Ct为

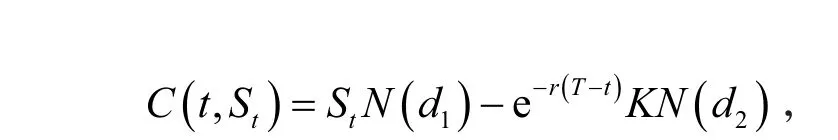
证明由定理1得Ct满足偏微分方程(3)，且边界条件为C(T，S)=(S-K)+.令S=ex，C=V(t，x)，则易得

将上式代入式(3)，则有

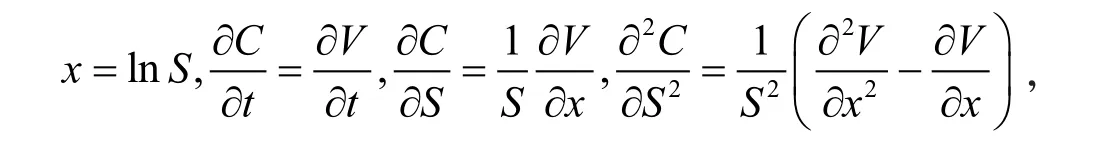
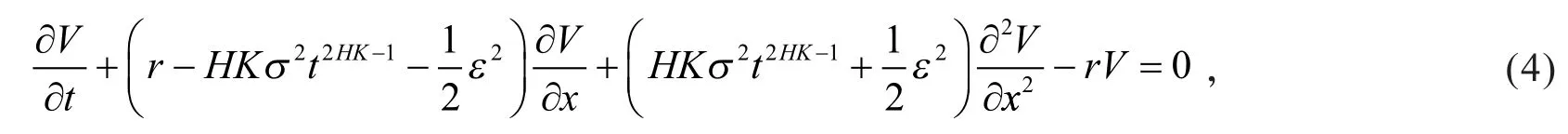
令

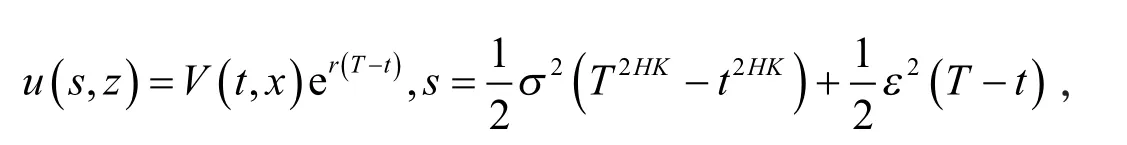
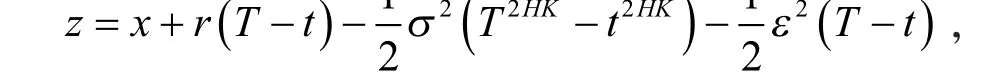
则有

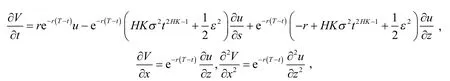
将上式代入式(4)，则有

根据热传导方程经典解理论[8]，式(5)有唯一强解

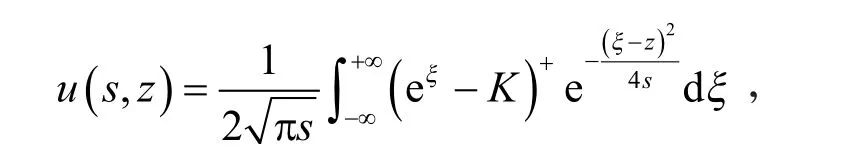
将边界条件代入可得

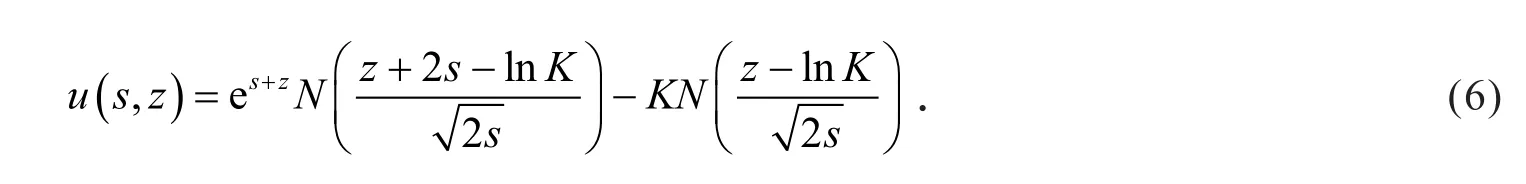
1

1

对式(6)做逆变换易得定理2成立.

推论1 当K=1时，可得到混合分数布朗运动驱动下的欧式看涨期权在t时刻的价格为

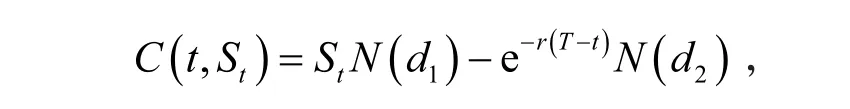
注1 该结论与文献[9](当n=1时)中得出的结果一致.

注2 当ε=0时，推论1的结果即为双分数布朗运动环境下欧式期权的定价公式，与文献[10]的结果一致.

采用类似的方法同样可以推导出欧式看跌期权的定价公式，不加证明地给出下面的定理.

定理3 假设到期日为T，履约价格为K，则混合双分数布朗运动下欧式看跌期权在任意时刻t∈ [0，T]的价格Ct为

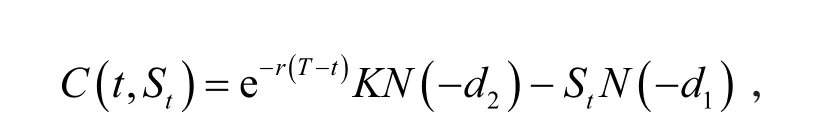
3 结论

本文假设标的资产由混合双分数布朗运动驱动，利用偏微分方程的方法探讨了欧式期权的定价问题.采用混合双分数布朗运动刻画金融资产的价格变化过程在一定程度上比传统模型有所改进，可以看作是混合分数布朗运动和双分数布朗运动驱动下的一种推广.另外，混合双分数布朗运动也可以应用于探讨奇异期权(如重置期权、障碍期权等)的定价问题.

[1] MANDELBROT B，VAN N J W. Fractional Brownian motion，fractional noises and application[J]. SIAM Review，1968，10：422-437.

[2] LIN S J. Stochastic analysis of fractional Brownian motion[J]. Stochastics and Stochastics Reports，1995，55(1/2)：122-140.

[3] BENDER C，ELLIOTT R J. Arbitrage in a discrete version of the Wick-fractional Black-Scholes market[J]. Mathematics of Operations Research，2004，29(4)：935-945.

[4] BJǒ RK T，HULT H. A note on Wick products and the fractional Black-Scholes model[J]. Finance and Stochastics，2005，9(2)：197-209.

[5] LEI P，NUALART D. A decomposition of the bi-fractional Brownian motion and some applications[J]. Statistics and Probability Letters，2009，79(5)：619-624.

[6] RUSSO F，TUDOR C. On the bifractional Brownian motion[J]. Stochastic Processes and their applications，2006，116(5)：830-856.

[7] ALOS E，MAZET O，NUALART D. Stochastic calculus with respect to Gaussian processes[J]. Annals of Probability，2001，29(2)：766-801.

[8] 邵宇，刁羽. 微观金融学及其数学基础[M].北京：清华大学出版社，2008：663-674.

[9] 徐峰，郑石秋. 混合分数布朗运动驱动的幂期权定价模型[J]. 经济数学，2010，27(2)：8-12.

[10] 赵巍. 分形市场视角下的期权定价模型及其套期保值策略研究[J].合肥工业大学学报：自然科学版，2013，36(11)：1388-1392.

(责任编辑：沈凤英)

Pricing European Option in a Mixed Bi-fractional Brownian Motion

XU Feng
(Business School，Suzhou Vocational University，Suzhou 215104，China)

Assuming that the underlying asset is driven by the mixed bi-fractional Brownian motion，this paper proposes a partial differential equation formulation for valuing European option by hedge principle. Moreover，using the boundary condition and the method of variable substitution，we obtain the solution to this partial differential equation-the pricing formula for European option.

mixed bi-fractional brownian motion；european option；pricing；long memory

F830.9；O211.6

A

1008-5475(2015)01-0050-04

2014-10-30；

2014-11-28

苏州市职业大学创新基金资助项目(2013SZDYY05)

徐 峰(1980-)，男，江苏泰兴人，讲师，硕士，主要从事金融数学研究.