不确定性参数灵敏度分析的随机响应面法*

方圣恩 张秋虎 林友勤 张笑华

(1.福州大学土木工程学院，福州 350116)(2.合肥工业大学土木与水利学院，合肥 230009)

引言

数值和数学模型已广泛应用于复杂工程问题的模拟和计算，以进行结构设计和优化、静动力分析、缺陷或损伤诊断、安全性评估等［1］.但现实结构中总存在着不确定性，在分析大量结构参数时容易导致分析结果的失真和矛盾，同时又需耗费大量的计算成本［2］.因此，灵敏度分析(sensitivity analysis，缩写SA)［3］对确定模型参数来说是十分必要的，其通过量化参数不确定性对响应变异性(比如方差)的贡献来识别参数重要性［4］.具体分为参数主效应(main effects)分析和相互效应(interaction effects)分析.

目前已有的SA方法大多基于数学或统计学方法，各有其适用范围［5］.可以一次单独分析一个参数，也可以采用随机抽样的方式同时分析多个参数［6］.然而对同一个问题，不同的SA方法可能给出不同的判断结果.Saltelli等［3］将SA方法分为散点图(scatterplot)法、导数(derivatives)法、回归系数(regression coefficients)法及方差(variance-based)法等四大类.各种方法分别对应于线性或非线性模型的基本假设，有着各自的优缺点.散点图可以将参数和响应间关系通过可视化方式体现出来，非常直观，但是判断上往往带有主观性且无法自动获取相关灵敏度指标［7］.通过偏微分求导的方式则要求参数—响应间关系可以函数化，该方法容易理解且计算效率高，但仅能对参数设计点附近小范围内的不确定性进行分析，无法提供灵敏度的全局信息［8］.此外，通过对参数—响应样本进行线性或非线性回归，可以搜索整个参数不确定性空间，得到的标准回归系数往往就是灵敏度指标［9］.但为了得到足够的分析精度，回归法往往需要大量的样本，导致对复杂模型来说计算量大为增加，实用性不强.最后，方差法可以很好地了解模型的灵敏度组成模式，尤其适用于模型的线性、单调性和可叠加性未知的情况［10，11］.方差法基于条件方差的计算，分解出各参数对响应方差的独立影响，同时还能估计高阶相互效应的影响.但这种方法实现过程比较复杂，计算量大，不利于实际应用.因此，可以在SA过程引入meta-model(如Kriging模型)来快速进行参数—响应间的不确定性传播，以大幅提高计算效率［12，13］.但传统meta-model对参数总体效应和高阶相互效应的估计精度往往不足.由此可见，一个好的SA方法要具备全局性、计算高效性和实用性强等特点.

有鉴于此，本文结合随机响应面(stochastic response surface，缩写SRS)，利用偏导方式求解得到参数灵敏度系数，以量化参数对响应变异性(单位响应变化)的贡献率.所提出方法通过数值梁进行验证，并与方差分析(analysis of variance，缩写ANOVA)法进行对比，验证了本文方法的正确性.

1 随机响应面理论

随机响应面可以看作是对确定性响应面理论的扩展，前者通过基于Hermite多项式的多项式混沌展开式(polynomial chaos expansion)来建立不确定性参数x和响应y之间的联系［14］:

式中ξ={ξi}表示服从标准正态分布N(0，1)的标准随机变量，是原参数向量x的变换;ai为表达式各项的系数，通过回归方式求解;Γp(·)表示多维p阶Hermite多项式［14］:

将x转换为ξ可以保证Γp(·)的正交性，即E [ Γp·Γq]=0(p≠q).对SA来说，这种转换能保证分析过程同等对待(无量纲化)不同类型的参数.然后通过概率配点法［14］(probabilistic collocation method)计算拟合SRS所需的样本，再利用回归分析求得ai，最后得到SRS的显式多项式表达式.相关理论的详细介绍可以参阅文献［14］，本文不再具体阐述.

2 灵敏度分析的随机响应面法

本节中基于公式(1)推导参数的灵敏度系数矩阵.首先对ξ(而非x)求偏导数，以此同等对待不同类型的参数.同时考虑到偏导数问题往往难以求解，需要结合数值分析方法，使得求解过程复杂化.而SRS表达式中的参数本身就是随机参数，且多项式分解后对ξ求偏导容易实现.此外，求解过程考虑了参数不确定性的完整空间，是一种全局方法.这里以常用的二阶SRS为例:

响应y对ξi偏导的期望值为:

式中随机标准变量的均值为0，即E(ξi)=0.因此，向量y=(yk)(k=1，2，…，m)的偏导矩阵θ可以表示为:

所对应的期望值矩阵为:

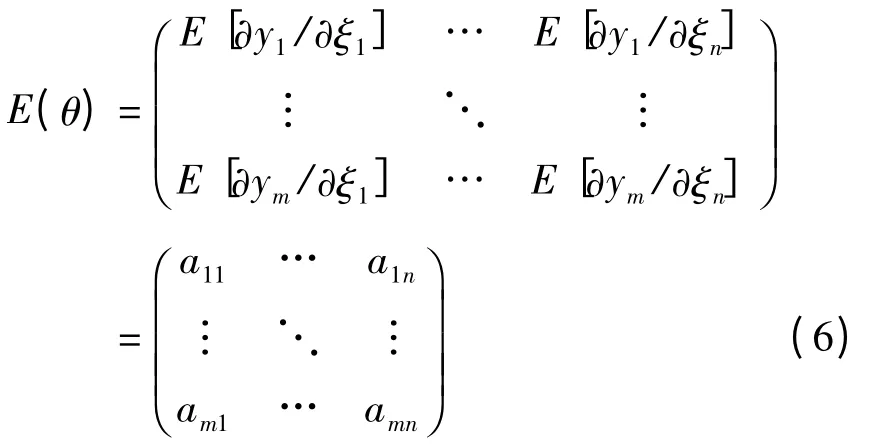
式中矩阵元素aki即式(1)中一阶项的系数，其代表了参数对响应的主效应.该结论可以通过3参数的2阶SRS来证明，其中xi=μi+σiξi(i=1，2，3).即:

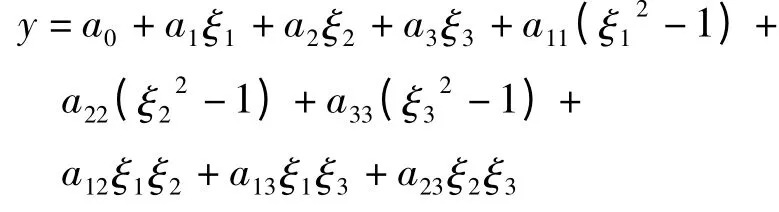
由此求得:

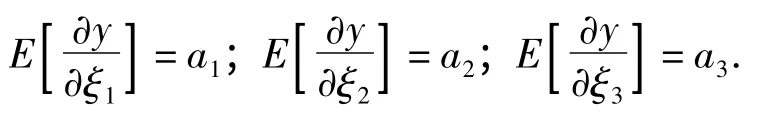
同时，y对原参数(x1，x2，x3)的偏导数为:

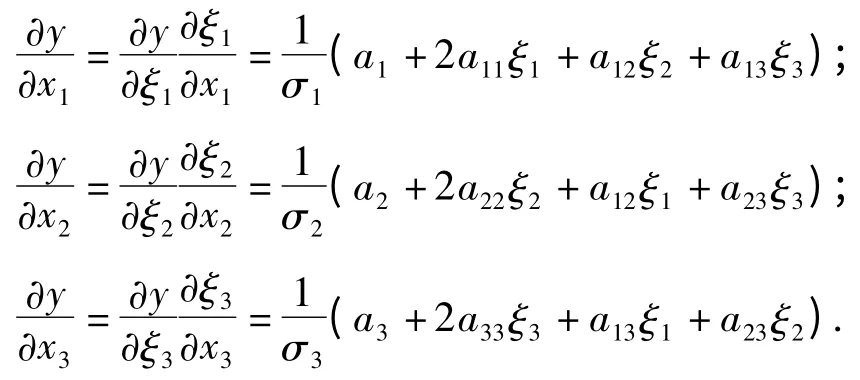
式中σi(i=1，2，3)是参数xi的标准差.因此容易求得:

因为xi的概率分布是已知的，E［∂y/∂xi］实际上是对应于xi均值的常数(假设为bi)，所以可以进一步得到:

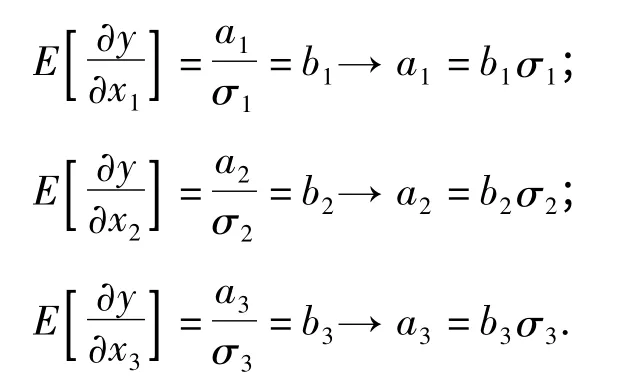
由上式可见，系数ai实际上综合考虑了xi的均值和标准差，其中均值可以看作是参数xi的确定性部分，而标准差则代表了不确定性部分，相当于传统灵敏度分析中的“对参数扰动”，而这种“扰动”必须基于参数的某个设计点，即本文中的均值.若是标准差脱离了均值进行分析，那就失去了SA的意义.最后值得一提的是，系数ai是一种稳定估计，即更高阶(如3阶)SRS表达式中一阶项所对应的ai几乎不会有变化［14］，这一特点对本文提出的SA方法来说是有利的.因为在构建metamodel时，可能无法确定模型的阶数，若是基于高阶和低阶模型得到的SA结果是不同的，那么灵敏度分析方法也就失去了可靠性.但是采用SRS则不存在这个问题，因此其具有更优的适用性.

3 灵敏度分析的方差分析法

为了进行比较，本文同时采用了ANOVA法估计参数不确定性对响应变异性的影响.ANOVA通过估计不同样本组的组间与组内均方(mean of square)来研究样本不确定性或误差的来源［15，16］，其中样本来源于服从正态分布的总体.ANOVA法可以分离各参数的效应，以估计参数对模型总体变异性的独立影响，或不同参数组合相互效应对模型总体变异性的影响.具体实施上，本文采用了2k因子设计［15，16］(2kfactorial design，缩写2kFD)来实现参数的SA.该设计基于ANOVA，每个参数仅有2个水平(可看作上下界值)，通过实验设计方法得到不同的参数和水平组合，在通过试验或数值计算求得样本;然后通过回归分析拟合样本得到一个线性模型，模型表达式的各项系数即相当于参数不确定性的效应系数.

4 算例

本文基于数值悬臂梁(图1)来验证所提出方法的可行性和可靠性.采用数值算例可以避免试验数据中混杂了其他的不确定性来源(比如环境噪声、人为误差等)，这些不确定性可能导致分析过程无法辨别响应变异性是否源于参数的不确定性，导致分析目标不明确.

图1 数值悬臂梁示意图Fig.1 Schematic diagram of the numerical cantilever beam

所采用的悬臂梁长2 m，截面尺寸0.2 m×0.2 m;材料参数为杨氏模量(E)30 GPa，密度(D)2400 kg/m3，泊松比(P)0.2.上述几何参数与材料特性均假设为名义值(均值).梁的有限元模型被划分为20个相同梁单元，并假设单元10包含了4个不确定性参数E、I(截面惯性矩)、D、P，以此分析参数不确定性对梁前5阶振动频率的影响.此外，由图2可见，梁的5阶振动模态中包括了4阶弯曲模态和1阶轴向变形模态.

图2 悬臂梁振动模态Fig.2 Vibrational modes of the cantilever beam

本算例设计了两种情形:1)参数不确定性水平相同，即每个参数的名义值作为均值，而表示不确定性的标准差设为1%;2)参数不确定性水平不同，即假设I的标准差为2%，其他3个参数的标准差仍为1%.第一种情况可以在同等条件下估计参数灵敏度，而第二种情况则考虑到现实结构中不同参数的不确定性水平可能不同，因此需要区别对待.

4.1 参数不确定性水平相同

首先建立包含4个参数的2阶SRS，即通过概率配点法得到20个样本，然后基于回归分析求得SRS的表达式系数.由第2节可知，表达式中1阶项的系数反映了各参数对频率的主效应.与此同时，为了进行比较，还利用2kFD进行SA，所需的样本数为24=16.两种方法的SA结果分别列于表1和2，其中为了便于比较，表中数值为当频率发生单位变化时，各参数对频率变异性的贡献率.

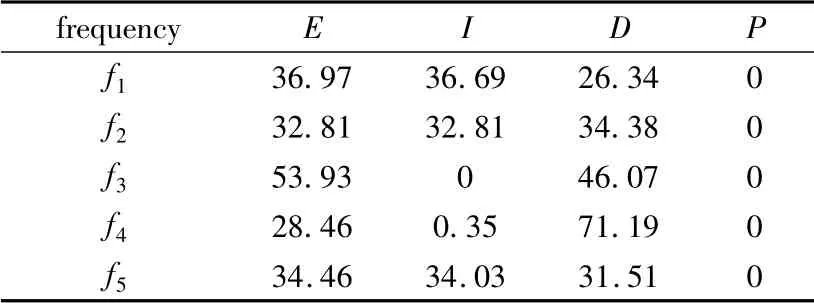
表1 参数不确定性对频率变异性的贡献率(情形1:SRS)Table 1 Parameter uncertainty percentage contributions to frequency variability(scenario 1:SRS)

表2 参数不确定性对频率变异性的贡献率(情形1:ANOVA)Table 2 Parameter uncertainty percentage contributions to frequency variability(scenario 1:ANOVA)

由表可见，两种方法给出了完全一致的分析结果，验证了本文方法的正确性.对第1阶频率而言，E和I的贡献率相同，且比D高10%左右，说明联系单元10截面抗弯刚度的参数对频率的影响比密度大;而在第2、5阶频率上，E、I、D三者的贡献率基本相同.同时对第3阶轴向变形模态来说，截面惯性矩I此时不起作用，因为其仅和抗弯刚度相关，与截面轴向刚度无关;而且在第4阶模态上，由于单元10处于模态节点处，此时I的影响也几乎为零.值得注意是，P对所有5阶频率都没有任何影响.上述观察结果可以通过悬臂梁振动频率的理论公式［17］来解释:

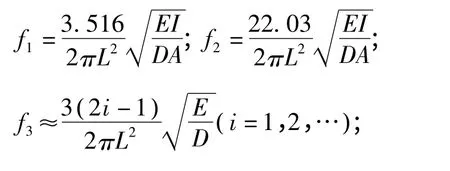
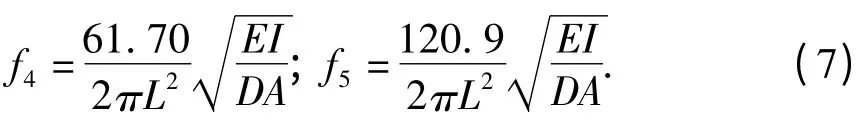
式中L和A分别表示梁长和截面积.由上式可见，对弯曲频率来说，E、I、D的影响应该是相同的;而P对频率则无任何影响.算例分析中，第1阶频率中D的贡献率可能受到单元10在1阶模态振型中位置的影响，此时E、I的影响会变大一点.这点推测可以在第4阶频率的分析中得到证实:该阶模态振型中单元10正好处于模态节点处，使得此单元的抗弯刚度EI不发挥作用(主要是截面惯性矩I不起作用)，因此I的影响几乎为0.而同样作为材料参数，此时D的贡献率却是E的2.5倍，说明E的影响也被大大削弱了.最后，对第3阶轴向振动模态来说，仅E和D对频率的变异性有贡献，这点和理论公式一致.由上述分析可见，SA可以有效地对参数不确定性的影响进行量化，从而发现对分析模型重要的参数.理论公式虽然能一定程度上反映问题，但容易造成误判(因为理论公式中的参数是对整根梁而言的，而不是针对某个局部单元)，特别是对复杂工程结构来说，通常无法得到频率的理论公式，此时SA方法更能体现其价值.

最后要说明的是，表1、2仅给出了参数的主效应，因为本算例中参数的相互效应影响非常小(EI、ED和ID对5阶频率的总体贡献率仅分别为0.40%、0.28%、0.02%、0.51%和0.31%)，所以未考虑.由此可以认为频率的总体变异性是各参数不确定性独立影响的叠加.

4.2 参数不确定性水平不同

本小节中根据E、I、D的不同不确定性水平，重新构建了SRS和2kFD进行分析，结果列于表3和4.基于4.1节的分析结果，本分析中不再考虑P.由表可见，在I增加了1倍的不确定性后，第1、2、5阶频率中I的贡献率也变成了E和D的2倍.该结果是合理的，因为在频率理论公式中3个参数的权重是相同的.同时对剩下的两阶频率而言，此时I依然没有影响，即便其不确定性水平提高了1倍，原因还是I对这两阶模态不相关，这从另一方面也说明了上节的分析结果是正确的.最后，对第4阶频率来说，D的贡献率仍然是E的2.5倍，说明其没有受到I不确定性水平改变的影响，同时也证明了上节的分析结果是正确的.

4.3 方法适用性讨论

由算例结果可知，SRS法给出的SA结果是可靠和准确的.但也存在一个问题，即既然ANOVA法可以给出准确的分析结果，那么提出SRS法是否必要?为此从以下几点进行讨论.首先，SRS和ANOVA方法都要求参数不确定性服从正态分布，从这点上说，二者皆属于概率SA法.但要注意的是，SRS可以直接给出不确定参数和响应间关系的随机表达式，应用上更简便，同时可以表示参数和响应的非线性关系;而2kFD建立的是线性模型，要求参数和响应间不存在强非线性.同时，2kFD分析时仅考虑参数的上下界，而对界限内的概率分布情况是一种弱要求，这对ANOVA分析的结果是有一定的影响的;而SRS理论则是完全基于参数概率分布假设的，分析过程更严格.最为重要的是，对拥有较多参数的复杂结构来说，2kFD所需的样本数呈指数级增长，使得计算成本激增.比如10个参数情况，2kFD至少需要210=1024个样本;而相同参数数目下，SRS仅需要132个样本，计算量上要小得多.由上述分析可见，两种方法各有其自身的适用范围，在某些情况下，SRS法更具优势.

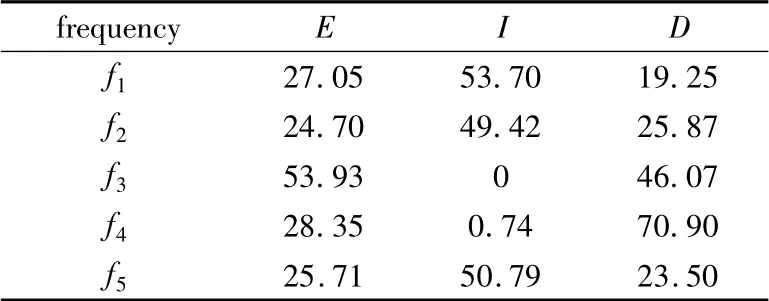
表3 参数不确定性对频率变异性的贡献率(情形2:SRS)Table 3 Parameter uncertainty percentage contributions to frequency variability(scenario 2:SRS)

表4 参数不确定性对频率变异性的贡献率(情形2:ANOVA)Table 4 Parameter uncertainty percentage contributions to frequency variability(scenario 2:ANOVA)

5 结论

本文针对工程中不确定性参数的灵敏度分析问题，提出了一种随机响应面法，即基于对SRS表达式的偏导求解，推导出参数灵敏度系数，实现对参数不确定性影响的量化.文中基于一根包含不确定单元参数的数值悬臂梁来验证所提出的方法，并与ANOVA法进行对比.分析结果表明，本文方法可以准确地估计参数灵敏度，并给出各参数对频率响应变异性的贡献率，使得灵敏度分析结果更客观.同时，SRS的构建过程无需大量样本，在计算成本上有着一定的优势.最后，所提出的方法可以进一步应用于复杂结构的参数灵敏度分析上.

1 Saltelli A，Tarantola S，Campolongo F，Ratto M.Sensitivity analysis in practice:a guide to assessing scientific models.Chichester:John Wiley＆Sons Ltd，2004

2 Hornberger G M，Spear R C.An approach to the preliminary analysis of environmental systems.Journal of Environmental Management，1981，12:7～18

3 Saltelli A，Ratto M，Andres T，Campolongo F，Cariboni J，Gatelli D，Saisana M，Tarantola S.Global sensitivity analysis:the primer.Chichester:John Wiley＆Sons Ltd，2008

4 Chan K，Saltelli A，Tarantola S.Sensitivity analysis of model output:variance-based methods make the difference.In:Proceedings of the 1997 Winter Simulation Conference，Atlanta，USA，1997

5 Iman R L，Helton JC.An investigation of uncertainty and sensitivity analysis techniques for computer models.Risk Analysis，1988，8(1):71～90

6 Hamby D M.A review of techniques for parameter sensitivity analysis of environmental models.Environmental Monitoring and Assessment，1994，32(2):135～154

7 Chan Y H，Correa CD，Ma K L.The generalized sensitivity scatterplot.IEEE Transactions on Visualization and Computer Graphics，2013，19(10):1768～1781

8 Punzo V，Ciuffo B.Sensitivity analysis of car-following models:methodology and application.In:Proceedings of the 90th Transportation Research Board Annual Meeting，Washington，2011

9 Ratto M，Pagano A，Young P.State dependent parameter metamodelling and sensitivity analysis.Computer Physics Communications，2007，177(11):863～876

10 Cukier R I，Levine H B，Shuler K E.Nonlinear sensitivity analysis of multiparameter model systems.Journal of Computational Physics，1978，26(1):1～42

11 Saltelli A.Making best use of model evaluations to compute sensitivity indices.Computer Physics Communications，2002，145(2):280～297

12 Storlie C，Helton J.Multiple predictor smoothing methods for sensitivity analysis:description of techniques.Reliability Engineering and System Safety，2008，93:28～54

13 Ciuffo B，Punzo V，Qualietta E.Kriging meta-modelling to verify traffic micro-simulation calibration methods.In:Proceedings of the 90th Transportation Research Board Annual Meeting，Washington，2011

14 Isukapalli S S.Uncertainty analysis of transport-transformation models［PhD Thesis］.New Brunswick Rutgers:The State University of New Jersey，1999

15 Montgomery D C.Design and analysis of experiments(6th edition).New York:J.Wiley＆Sons，2004

16 Myers R H，Montgomery D C，Anderson-Cook C M.Response surface methodology:process and product optimization using designed experiments(3rd edition).New York:John Wiley＆Sons，2009

17 Chopra A K.Dynamics of structures:theory and applications to earthquake engineering(4th Edition).Upper Saddle River:Prentice Hall，2011