考虑司机反应延迟和次近邻车辆影响的格子模型*
2015-03-01杜勇武佳尹吉庆叶双双
杜勇 武佳 尹吉庆 叶双双
(武警后勤学院基础部数学教研室,天津 300309)
前言
通过研究交通流的动力学模型人们发现处于自由流和阻塞流之间的交通流存在着阻塞转移的现象.后来有一些学者运用非线性分析的方法对这种现象进行了研究,如Kurtze和Hong从交通流的流体力学模型中导出了KdV方程[1],他们展示了中性稳定性曲线附近出现的孤立子.Komastsu和Sasa[2]运用同样的方法在车辆跟驰模型也推导出了mKdV方程,通过在临界点周围时出现的扭结—反扭结的密度波来描述交通阻塞现象.同时在扩展模型[3]和差分方程模型[4,5]中也可推导出mKdV方程.说明几类主要模型都能描述交通流的堵塞转移现象.为了更加真实描述交通流现象,T.Nagatani提出了关于时间连续空间离散的单车道格子流体力学模型[6],为交通流的研究开创了一个新的方向.2004年薛郁在一维交通流格子模型的基础上,分别考虑最近邻和次近邻车以及考虑前、后近邻车相互作用进行车辆优化的交通流格子模型[7],结果显示次近邻车辆信息对模型有致稳作用.祝会兵从分析司机的细致行为出发,提出了考虑司机反应延迟的格子流体力学模型[8],指出延迟时间越长越容易造成交通阻塞.该模型未引入次近邻车辆因素.
本文在车辆次近邻交互跟驰模型和司机反应延迟模型的基础之上,基于次近邻车辆对格子模型的致稳作用和司机反应延迟时间对格子模型稳定性破坏作用,提出了基于司机反应延迟的次近邻车辆交互的格子模型,能够更加真实地反映行驶车辆的交通流行为.
1 考虑司机反应延迟和次近邻车辆交互影响的格子流体力学模型
通过改进优化流量函数提出如下格子流体力学模型,

上式中第一个方程是流体力学的连续性方程的空间离散形式,由方程

得到,反映了车辆数守恒.第二个方程为车流量控制方程,由方程

离散化后得到,其中V(ρ(x))为优化速度函数[8],

vmax是车辆运行的最大速度;hc为车辆行驶的安全距离;τ为时间步长;a为司机敏感系数.(1)中j表示一维格子的j点,ρj,vj分别表示j点处t时刻的车流密度和速度;ρ0为平均密度,空间步长为平均车头距1/ρ0.τ为车辆延迟时间,可以分为机械延迟和司机延迟,其中nτ表示司机的延迟时间,n为权重,车辆流量的调整由于司机的反应延迟会出现时滞.(1)中第二个方程表示在位置j处时刻t时的流量ρjvj需要j+1和j+2处t-nτ时的流量来控制,其中等号右侧第二式为近邻与次近邻车辆之间的优化流量差,γ为权重系数.
把(1)第二个方程带入第一个方程,消去ρjvj化简得密度方程

2 线性稳定性分析
首先考虑均匀交通流的稳定性.定义密度为常数ρ0,速度为常数V(ρ0)时的交通流为均匀交流.方程(2)在均匀流时的解为

令yj(t)为均匀稳定流的小扰动,则有ρj(t)=ρ0+yj(t).然后,代入(2)得到方程在线性化之后的方程为

通过展开yj(t)∝exp(ikj+zt),得到关于z的如下方程

再展开z=z1(ik)+z2(ik)2+…,代入上式,得到ik的一阶和二阶系数

如果z2是负值,那么这种均匀稳定的交通流在长波模式下就是不稳定的.如果z2为正值,那么均匀流是稳定的.因此,中性稳定性的条件为z2=0,即

对于长波模式下的小扰动情形,τ在满足下列条件时,均匀流是不稳定的.即

优化速度的导数V'(ρ0)当ρ0=ρc(ρc为临界密度)时取到最小值.如果τ<τc,那么均匀流在不考虑密度的情况下往往是稳定的.ρ=ρc,τ=τc临界点.
由(7)可知,n=0时,a会随着γ的增加而减小,行驶车辆对于交通阻塞的敏感度会下降,模型的稳定性增强.当γ=0时,a会随着n的增加而增加,模型的稳定性减弱.
3 非线性分析及mKdV方程
运用约化摄动法对模型进行非线性稳定性分析.考虑模型粗颗粒下的长波模式,描述长波模式的最简单的方法就是长波的泰勒展开.因在临界点(ρc,τc)附近的长波变化会出现慢变量行为,故当0<ε≪1时,定义慢变量

其中b为常数.假设密度:

把以上式子带入(2)中展开到ε的5次幂,则得到如下的偏微分方程
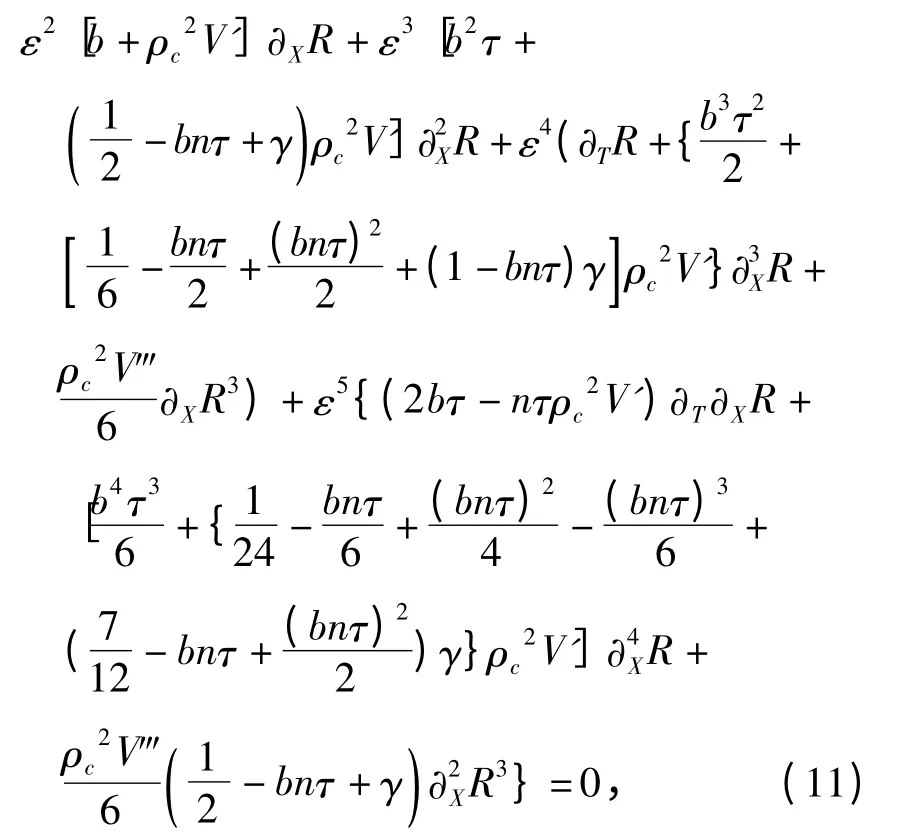
其中,


其中,

式(11)可化为方程

其中

作变换
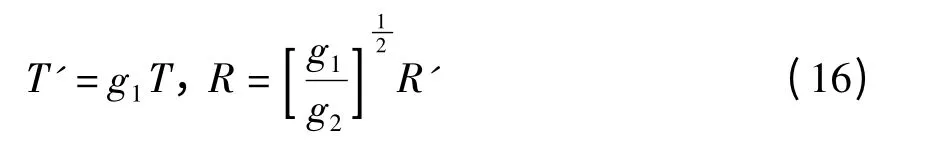
把(16)中的变换代入到(14),得到(14)的规范化方程为

如果忽略(17)中的O(ε)项,(17)就是mKdV方程,且有扭结孤立波解

基于R'(X,T')=R'0(X,T')+εR'1(X,T'),需要正确的考虑O(ε).为了选择扭结解(18)中的传播速度c的值,需要满足如下可解条件

其中,

通过积分(19),并仿照文献[9]的计算得到

于是把(21)和(16)代入(18)中得到方程(17)的解

到扭结解的振幅
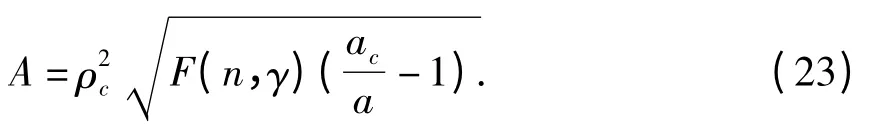
其中

其中,

因扭结解代表共生相,所以式(22)既包含低密度自由流相位也包含高密度的阻塞相位,分别用ρ=ρc-A,ρ=ρc+A表示.得到坐标系(ρ,a)下相图(图1).由ρ=ρc-A得到密度与敏感度的关系
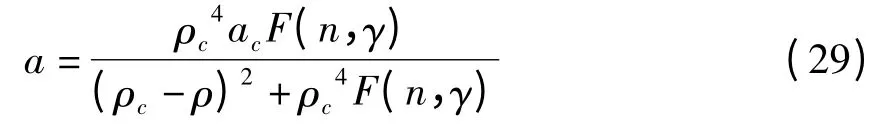
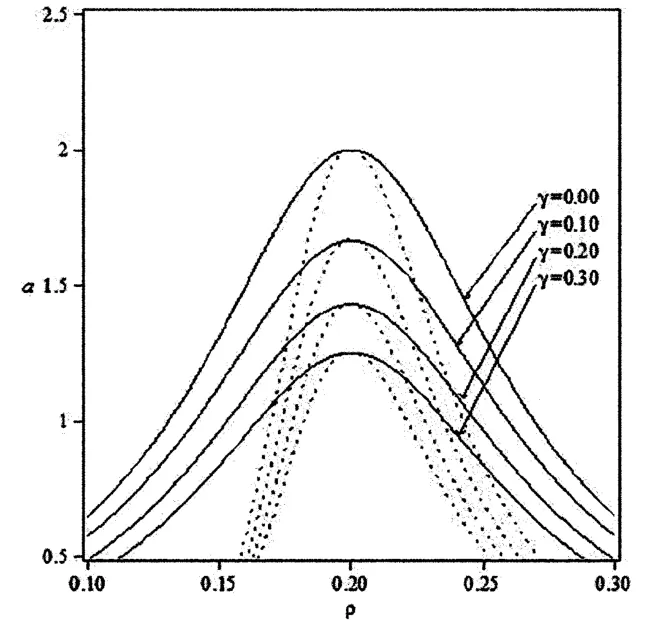
图1 取不同值时密度-敏感度相图Fig.1 The phase diagram on(ρ,a)-plane for n=0
图1描述n=0,γ分别取0,0.1,0.2,0.3时密度-敏感度相图,即中性稳定性与共存曲线的相图.其中共存曲线与中性稳定性曲线,分别用实线与虚线表示.由图可知,随着γ的增大,共存曲线与中性稳定性曲线都越来越低,不稳定区域越来越小(阻塞的区域越来越小)即稳定区域越来越大,说明交通流的稳定性增强.因此,次近邻车辆的行为对格子流体力学模型有一定的致稳作用,而且这种作用随着强度系数的增大而增大.结论与薛郁优化车辆的流体力学格子模型[7]的结果相符.
下面进行参数分析.首先,令F(n,γ)=C,(C为常数)即为参数n,γ的关系式.如图2所示n与γ成负相关,由曲线的斜率逐渐增大可知,随着n的增大γ也变化的越来越快.相同条件下,n的扰动相对γ来说对模型稳定性的影响会更大.

图2 参数关系图Fig.2 The relation diagram on(n,γ)-plane

图3 n,γ取不同值时密度-敏感度相图Fig.3 The phase diagram on(ρ,a)-plane for obtaining the different with n,γ
通过共存曲线来进一步论证上述结论.图3描述n取0.05,0.1,0.15时,γ分别取值0.1,0.2,0.3时的密度—敏感度相图,作者只分析参数变化对共存曲线的影响.因为车辆反应延迟主要来自机械延迟,司机反应延迟只占其中的小部分,所以n分别取值0.05,0.1,0.15.图3中n=0.05用点线表示,n=0.10用破折线表示,n=0.15用直线表示.图中最上面三条线是γ=0.1的情形,中间是γ=0.2的情形,最下面是γ=0.3的情形.通过观察图3分析发现,γ取相同值时,敏感系数ac随着n越大不断增大,共存曲线的位置不断上升,稳定区域不断减小.表明司机的敏感程度减弱,或者说当司机感知车头间距的延迟时间增大时交通拥堵现象更容易发生,这与实际交通现象时吻合的.也和文献[8]的结论相同.
4 结论
本文模型中综合考虑司机反应延迟和次近邻车辆两因素,既考虑了司机细致行为又考虑交通流动力学行为对运行车辆的调整.两个因素成负相关,对模型稳定性起相反作用,共同造成交通流的复杂性.薛郁优化车辆的流体力学格子模型[7]和祝会兵基于司机反应延迟的流体力学格子模型[8]是本模型的特殊情形.说明本文结论正确,符合实际交通流行为,同时也说明模型更全面的反映交通流的实际行为.
1 Kurtze D A,Hong D C.Delay effect on phase transitions in traffic dynamics.Physical Review E,1995,5(2):218~225
2 Komatsu T,Sasa S.Kink solution charactering traffic congestion.Physical Review E,1995,52:5574~5582
3 Nagatani T,Nakanishi K.Delay effect on phase transitions in traffic dynamics.Physical Review E,1998,57(6):6415~6427
4 Nagatani T,Nakanishi K,Emmerich H.Phase transition in a difference equation model of traffic flow.Physica A,1998,31:5431
5 Nagatani T.Stabilization and enhancement of traffic flow by the next-nearest-neighbor interaction.Physical Review E,1999,60(6):6395~6401
6 Nagatani T.TDGL and MKdV equations for jamming transition in the lattice model of traffic.Physical A,1999,264:581~592
7 薛郁.优化车流的交通流格子模型.物理学报,2004,53(1):25~30(Xue Y.Lattice models of the optimal traffic current.Acta Physica Sinica,2004,53(1):25~30(in Chinese))
8 祝会兵.基于驾驶行为细致分析的交通流建模与模拟[博士学位论文].上海:上海大学,2008(Zhu Huibing.Traffic flow modeling and simulation based on a detailed analysis of driving behavior[PhD Thesis].Shanghai:Shanghai University,2008(in Chinese))
9 Ge H X,Cheng R J,Dai SQ.KdV and kink-antikink soluti-ons in car-following models.Physica A,2005,357:466~476
10 杜勇,化存才,郑志波,袁娜.一种岔路口分流交通流格子模型的孤立波阻塞分析.动力学与控制学报,2013,11(2):133~136(Du Y,Hua C C,Zheng Z B,Yuan N.Analysis of soliton in a split-flow traffic flow lattice model on the crossing road.Journal of Dynamics and Control,2013,11(2):133~136(in Chinese))
