神经元高低状态切换发放的神经动力学*

徐旭颖 王如彬

(华东理工大学理学院认知神经动力学研究所，上海 200237)

引言

动物不同的行为状态反映在大脑中是由脑整体活动的不同模式引起的.神经电生理实验表明，动物在被麻醉条件下的初级视皮层可以观察到慢波睡眠现象［1，2，3］，而从非麻醉动物清醒状态下体感皮层所观察到的现象中发现［4］，神经元膜电位可以在“高”、“低”两个不同状态之间进行自发的周期性切换［5］.

这种阈下活动的特点是神经元膜电位呈现出双峰分布的现象.实验表明这种“高”、“低”状态之间的切换也可以由感知刺激引起［1，4，6，7］.有趣的是这种由感知刺激引起的切换与神经元自发进行的切换非常相似.在大鼠和猫的神经电生理实验中报道了另一种有兴趣的特征，即刺激的响应依赖于自发波动的状态.而这种波动状态依不同的动物实验而有所不同.当感知刺激作用在大鼠时，记录到的神经响应位于神经发放的“低状态”，这要比高状态时的神经响应强烈的多［4，7］.相反，在猫的感知刺激实验中，情况却正好相反［6］.这种具有高低状态切换的神经发放所产生的原因目前还不清楚.事实上对于神经元膜电位的各种表达模式以及神经网络之间的相互作用了解得仍然很少，特别是对于神经发放的编码模式和认知行为之间关系的理解还有很多困难.所以从还原论的角度出发，从最简单的单个神经元开始研究其状态切换这一现象对于深刻理解脑内的神经信息处理的机制无疑是一个很好的有效的研究方法.就实验的角度而言，目前神经电生理实验所能记录到的是单个或少数的很有限的神经元集群的活动，而无法也不可能在刺激作用下记录到大规模神经元集群中所有神经元的活动.然而单个神经元的实验数据是容易测得的，因此在探讨网络行为的神经动力学机制之前需要首先搞清楚单个神经元膜电位高低状态发放的动力学机制，它是我们研究认知行为与网络活动的基础.

实验表明激活单个皮层神经元可以对感知觉和运动输出起到调节作用［8，9］.同时还发现大鼠单个皮层神经元的重复性的高频簇发放可以触发皮层状态在慢波睡眠和快速眼动睡眠之间的切换［10］.这表现为受到刺激的神经元的膜电位由高幅低频振荡状态切换为低幅高频振荡状态，或与之相反.与此同时，神经网络局部场电位的模式也会随时间发生改变，可以用局部场电位来描述皮层整体的状态［17，18，19，20，23］.因此，单个皮层神经元的高低状态同时也能够反映皮层不同的整体状态，如高幅低频振荡和低幅高频振荡这两个状态分别类似于慢波睡眠和快速眼动睡眠［11，12，13］.这些结果都能够支持单个皮层神经元能够对动物的行为状态起到调节的作用［10］.

本文将通过单个神经元高低状态切换的动力学模型来模拟这种切换的特性:双稳定性、方向性和自发性［5，14］.所谓双稳定性，即神经元受到外界刺激后，可以稳定在一种状态，受到下一次刺激后，便会翻转稳定在另一个状态.这两个不同状态的切换可以分别由“高状态”和“低状态”来描述.也就是说，神经元在外界刺激下可以在高、低两个状态之间进行跳跃.而方向性是指神经元在高、低两个状态之间进行切换时并不是任意的.在特定的情况下，切换只能从“高状态”跳“低状态”，或者只能从“低状态”在跃迁到“高状态”.自发性则是指在没有任何突触输入的情况下，神经元可以在“高状态”和“低状态”之间进行自发的周期性的切换.

1 生物物理模型

基于H-H方程并根据浦肯野细胞的特点给出单个神经元的动力学模型如方程(1)-(5)所示.该类单个神经元的动力学模型［14］包含三类离子电流:一个瞬时的向内电流(这里指的是钠电流)，一个慢速h型电流，以及向外电流(这里指的是钾电流和漏电流).根据下述模型的数值模拟可以观察到神经电生理实验中的双稳定性、方向性和自发性，用以考察神经元双向切换的动力学机制.

其中，离子电流的表达式分别如下:

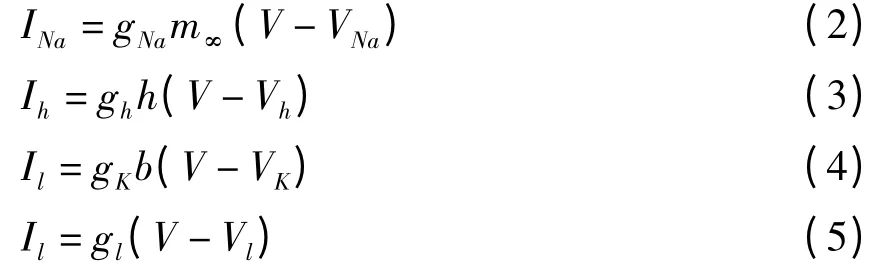
在浦肯野细胞中发现了两种向内电流，分别为钠电流和钙电流［15，16］.胞体浦肯野细胞的双稳定性与钠电流有关［15］，而树突的双稳定性与钙电流有关［16］.在本文的模型中，为简单起见仅使用钠电流.但事实上双稳定性应该是这两种电流共同作用的结果［14，21，22］.

在讨论神经元高低切换的双稳定性和方向性时，该模型包含了两个动力学变量，神经元膜电位V和h型电流的失活率h.在讨论神经元高低切换的自发性时，则在之前的基础上增加了一个动力学变量，钾电流的失活率b.关于h和b的动力学方程［14］如下:

方程(1)～(7)中，V表示神经元膜电位，INa，Ih，Ik，Il分别表示钠电流、慢速h型电流、钾电流和漏电流.gNa，gh，gK，gl分别表示钠电导、慢速h型电导、钾电导和漏电导，VNa，Vh，VK，Vl分别是对应的反转电位.m∞，h∞，b∞分别表示钠通道，h型通道和钾通道的失活项，h，b为对应通道的失活变量，τh，τb为对应突触时间常数.Tm，σm，Th，σh，Tb，σb，τ0b，aα，bα，kα，aβ，bβ，kβ为常数.

2 结果分析与讨论

2.1 切换发放的双稳定性

有两种刺激方式可以实现神经元在高、低两个状态之间的切换.一种是加入一个简单的外部电流，另一种则是瞬时提高钠电导至某一数值.

如图1所示，上图表示在10s的时间长度中，每隔2s加入一个持续时间为0.1s，强度为7.2μA/cm2的脉冲刺激电流;下图显示，在加入这些完全相同的刺激的时候，神经元的膜电位在高(-45mV左右)、低(-65mV左右)两个状态之间切换.

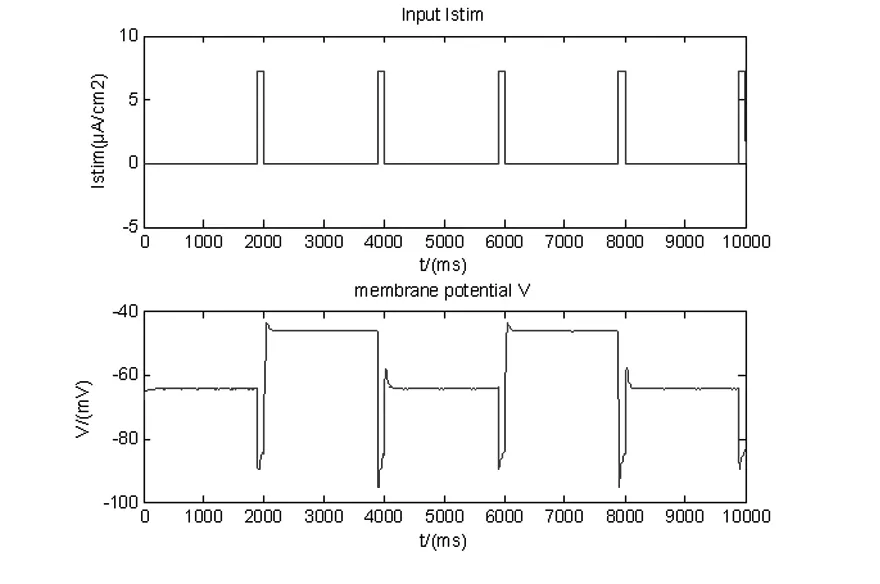
图1 加入外部电流Fig.1 Add a brief outward current

如图2所示，上图表示在10s的时间长度中，每隔2s或1s加入一个持续时间为4ms的刺激，使得钠电导的强度为从0.06mS/cm2瞬间增加至1.2mS/cm2;下图显示，在加入这些完全相同的刺激的时候，神经元的膜电位在高(-45mV左右)低(-65mV左右)两个状态之间切换，并且这种切换产生了比较复杂的发放:膜电位在瞬间超过0mV，并迅速回落，形如动作电位但又不完全是动作电位.

图2 瞬时提高钠电导Fig.2 Increase the sodium conductance instantaneously

以上两个结果说明该动力学模型能够描述神经元的双稳态特性.即神经元有两个稳定状态，其余均为不稳定的状态.当神经元受到外界刺激后，可以稳定在一种状态，受到下一次刺激后，破坏了原有的稳定状态，但是可以通过系统自身的调整翻转稳定在另一个状态.这两个状态分别是“高状态”和“低状态”.也就是说，神经元在外界刺激下可以在高、低两个状态之间进行切换.这种切换产生的可能机制是离子在细胞膜内外的运动.当钠电导瞬时提高至一定水平时，会引起轻度的去极化，使得少量的钠离子通道被激活并使之内流，从而引起去极化的幅度增大.同时增大的去极化又反过来激活更多的钠离子通道，导致大量钠离子内流.当到达膜电位最高点时，钠离子通道失活，h型通道激活，于是产生了膜电位的复极化现象，当膜电位减少到-45mV附近时，导致h型通道的开放受到抑制.此时，钾离子外流，钠离子内流达到新的平衡，即膜电位处于稳定状态.同时，根据h型通道受到抑制的不同，分别稳定在“高状态(-45mV)”或“低状态(-65mV)”.

2.2 切换发放的方向性

在本文给出的模型中，切换的方向性主要是依靠钾电导的不同来实现的.图3至图5分别描述了由于钾电导的取值不同造成的切换形式的改变.这三个图的上图分别表示膜电位的变化情况，即高低状态的切换，下图表示的是模型中的两个动力学变量V和h的相平面图.其中红色实线表示=0的点，而蓝色“+”号所连成的线则表示=0的点，这两条线的交点即黑色圆圈所标注的点就是系统的稳定点，也就是系统的两个稳定状态.其余的点都是不稳定的，即经过一段时间后最终都会停留在两个稳定状态之一.图中的绿色实线表示系统在受到刺激之后，从其中一个稳定点过渡到另一个稳定点的转迁过程.

如图3所示，上图表示gK=0.1mS/cm2时，在瞬时提高钠电导的外界刺激下，膜电位可以从“低状态”切换到“高状态”，在相同刺激下，也可以从“高状态”切换到“低状态”，也就是说此时的切换具有双向性;下图也同样表明，系统在这两个平稳的状态之间相互转迁.

图3 gK=0.1mS/cm2时的膜电位图及h-V相位图Fig.3 Membrane potential and h-V phase plane when gK=0.1mS/cm2

如果对钾电导的取值做一些增减后也可以观察到整个系统切换状态的改变.

图4 gK=0.09mS/cm2时的膜电位图及h-V相位图Fig.4 Membrane potential and h-V phase plane when gK=0.09mS/cm2

如图4所示，上图表示gK=0.09mS/cm2时，在同样的外界刺激下，膜电位可以从“低状态”切换到“高状态”，但是之后再给予同样的刺激，膜电位仍然处于“高状态”而不再变化到另一个稳定态，也就是说此时的切换具有单向性，仅能从“低状态”切换到“高状态”;下图也同样表明，系统只能从膜电位较低的平稳状态转迁到膜电位较高的平稳状态，然后绕着该平稳状态作周期性转迁.

图5 gK=0.105mS/cm2时的膜电位图及h-V相位图Fig.5 Membrane potential and h-V phase plane when gK=0.105mS/cm2

如图5所示，上图表示gK=0.105mS/cm2时，在同样的外界刺激下，膜电位可以从“高状态”切换到“低状态”，但是之后再给予同样的刺激，膜电位仍然处于“低状态”而不再变化到另一个稳定态，也就是说此时的切换具有单向性，仅能从“高状态”切换到“低状态”;下图也同样表明，系统只能从膜电位较高的平稳状态转迁到膜电位较低的平稳状态，然后绕着该平稳状态作周期性转迁.

以上的三个结果表明该动力学模型能够描述神经元在受到某种特定刺激后产生状态切换时可能具有的双向性或单向性.也就是说切换可以是任意方向的，即“高状态”到“低状态”，或“低状态”到“高状态”均可;也可以是单方向的，即只能从“高状态”到“低状态”，或者只能从“低状态”变化到“高状态”.

2.3 切换发放的自发活动

关于模型的双稳定性和方向性的讨论中，都需要加入外界刺激才能引起以上的各种变化.假如不考虑刺激条件，神经元是否还能进行这些状态的切换呢?事实上动物的在体或离体的实验记录都表明，神经元膜电位可以在“高”、“低”两个状态之间进行自发的周期性的切换［5］.因此需要进一步考察本文所给出的模型是否具有这种自发切换的能力.

由于之前的模型只含有两个动力学变量，过于简单没办法实现自发切换，于是我们在原有动力学模型的基础上增加一个动力学变量，即钾电流的失活率b.

计算结果如图6所示，上图为不加任何外界刺激的情况下，膜电位呈现出自发的周期性的两态切换的现象;而下图即膜电位的分布图，可以看出膜电位呈现出双峰分布的形式，也就是说膜电位基本处在高、低两个稳定状态之一.

图6 自发切换的膜电位及其分布图Fig.6 Membrane potential of spontaneous transitions and its distribution

从这个可以产生自发切换的模型中加入刺激，每隔2s或1s加入一个持续时间为4ms的刺激，使得钠电导的强度为从0.06mS/cm2瞬间增加至1.2mS/cm2，可得到图7和图8所示的计算结果.

图7 自发切换的模型中加入刺激Fig.7 Add stimuli to the model which can exhibit spontaneous transitions

如图7所示，上图显示了加入的外界刺激，主要是之前介绍过的瞬时提高钠电导的方法;下图结果显示，加入了外界刺激以后，能够自发切换的单个神经元发生切换的情况变得复杂了很多.其中黑色箭头表示神经元自发切换的情况;绿色箭头表示在给予外界刺激后神经元也做出切换;而红色箭头表示，就算给予外界刺激神经元却没有进行任何切换.这是由于能够自发切换的神经元本身有一个自身的稳定性，外界刺激的加入破坏了这种稳定性，所以它可能由一个稳定状态转迁到另一个稳定状态，也可能仍然转迁到自身原来的稳定状态.另一个值得注意的现象是从图中红色箭头和绿色箭头的比较中，我们发现，当神经元处于“低状态”时，它更容易受到外界刺激的影响从而发生状态的切换，而当其处于“高状态”时则不容易受到外界刺激而产生切换.因为从图中可以发现，中间的红色箭头处，虽然神经元处于“低状态”，但是它受到刺激后并没有产生切换.

图8显示的是膜电位的分布图，可以看到也是呈现出双峰分布的现象，即膜电位主要分布在高(-45mV)、低(-65mV)两个状态.

图8 膜电位分布图Fig.8 Distribution of membrane potential

以上的结果说明该动力学模型确实能够描述神经元进行自发的周期性切换的现象.并且在这种情况下，神经元对刺激的响应与自身所处的状态有一定的关系.相对而言，当神经元处在“低状态”时，对外界刺激的响应较大，这与已有的实验结果相符［4］，［7］.

3 结论

本文构造了单个神经元实现高低状态切换的动力学模型，该模型能够准确地描述这种切换的三个动力学特性:双稳定性、方向性和自发性，主要结论如下:

(1)当神经元受到外界刺激后，可以稳定在一种状态.受到下一次刺激后，便会翻转稳定在另一个状态.这两个状态分别是“高状态”、“低状态”.也就是说，神经元在外界刺激下可以在高低两个状态之间进行切换.

(2)神经元在受到某种特定刺激后所产生的状态切换具有双向性或单向性的特征.换句话说，切换可以是任意方向的，即从“高状态”切换至“低状态”，或从“低状态”切换至“高状态”均可;也可以是单方向的，即只能从“高状态”到“低状态”，或者只能从“低状态”变化到“高状态”.

(3)神经元也可以在自发的条件下做周期性的状态切换.并且在这种自发切换情况下，神经元对外界刺激的响应与自身所处的状态有一定的关系.相对而言当神经元处在“低状态”时，对外界刺激的响应较大.

上述结论与已经观察到的实验现象非常吻合［1，4-7］，说明本文提出的对单个神经元的两态切换的研究是成功的和有效的.我们的目标是研究神经元集群和网络行为的两态切换，以及了解神经元集群在耦和条件下单个神经元的两态切换对网络行为贡献的作用，以此作为了解单神经元和网络行为之间神经发放动力学机制的基础.

1 Anderson J，Lampl I，Reichova I，Carandini M，Ferster D.Stimulus dependence of two-state fluctuations of membrane potential in cat visual cortex.Nature Neuroscience，2000，3:617～621

2 Lampl I，Reichova I，Ferster D.Synchronous membrane potential iuctuations in neurons of the cat visual cortex.Neuron，1999，22:361～374

3 Steriade M，Nunez A，Amzica F.Intracellular analysis of relations between the slow(＜1Hz)neocortical oscillation and other sleep rhythms of the electroencephalogram.Journal of Neuroscience，1993，13:3266～3283

4 Petersen C C H，Hahn T T G，Mehta M，Grin-vald A，Sakmann B.Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex.In:Proceedings of the National Academy of Sciences，2003，100:13638～13643

5 Nestor Parga，Larry F，Abbott.Network model of spontaneous activity exhibiting synchronous transitions between up and down states.Neuroscience，2007，1:57～66

6 Haider B，Duque A，Hasenstaub A R，Yu Y，McCormick D A.Enhancement of visual responsiveness by spontaneous local network activity in vivo.Journal of Neurophysiology，2007，97:4186～4202

7 Sachdev R N S，Ebner F F，Wilson C J.Effect of subthreshold up and down states on the whisker evoked response in somatosensory cortex.Journal of Neurophysiology，2004，92:3511～3521

8 Brecht M，Schneider M，Sakmann B，Margrie T W.Hisker movements evoked by stimulation of single pyramidal cells in rat motor cortex.Nature，2004，427:704

9 Houweling A R，Brecht M.Behavioural report of single neuron stimulation in somatosensory cortex.Nature，2008，451:65

10 Cheng Y T，Li M M P，Yang D.Burst spiking of a single cortical neuron modifies global brain state.Science，2009，324:643～646

11 Steriade M，McCormick D，Sejnowski T.Thalamocortical oscillations in the sleeping and aroused brain.Science，1993，262:679

12 Destexhe A，Contreras D，Steriade M.Spatiotemporal analysis of local field potentials and unit discharges in cat cerebral cortex during natural wake and sleep states.Journal of Neuroscience，1999，19:4595

13 Gervasoni D，et al.Global forebrain dynamics predict rat behavioral states and their transitions.Journal of Neuroscience，2004，24:11137

14 Yonatan L，Séverine M，Paul C，Kazuo K，Haim S，Yosef Y，Michael H.Bistability of cerebellar Purkinje cells modulated by sensory stimulation.Neuroscience，2005，8:202～211

15 Llinas R，Sugimori M.Electrophysiological properties of in vitro Purkinje cell somata in mammalian cerebellar slices.Journal of Physiology，1980，305:171～195

16 Llinas R，Sugimori M.Electrophysiological properties of in vitro Purkinje cell dendrites in mammalian cerebellar slices.Journal of Physiology，1980，305:197～213

17 Wang R B，Zhang Z K，Chen G R.Energy coding and energy functions for local activities of brain.Neurocomputing，2009，73(1-3):139～150

18 Wang R B，Zhang Z K，Chen G R.Energy function and energy evolution on neural population.IEEE Transactions on Neural Networks，2008，19(3):535～538

19 Wang R B，Zhang Z K.Energy coding in biological neural network.Cognitive Neurodynamics，2007，1(3):203～212

20 Liu Y，Wang R B，Zhang Z K，Jiao X F.Analysis on stability of neural network in the presence of inhibitory neurons.Congnitive Neurodynamics，2010，4(1):61～68

21 汪雷，刘深泉.皮层锥体神经元模型的动力学分析.动力学与控制学报，2011，9(1):49～53(Wang L，Liu S Q.Dynamical analysis of cortical pyramidal neuron model.Journal of Dynamics and Control，2011，9(1):49～53(in Chinese))

22 王海侠，陆启韶，郑艳红.神经元模型的复杂动力学:分岔与编码.动力学与控制学报，2009，7(4):293～296(Wang H X，Lu QS，Zheng Y H.Complex dynamics of the neuronal model:bifurcation and encoding.Journal of Dynamics and Control，2009，7(4):293-296(in Chinese))

23 王如彬，张志康，沈恩华.大脑皮层内神经元集团的能量演变.动力学与控制学报，2008，6(1):55～60(Wang R B，Zhang Z K，Shen E H.Energy evolution of neural population in cerebral cortex.Journal of Dynamics and Control，2008，6(1):55～60(in Chinese))