多涡卷Chua混沌吸引子的设计与性能分析*

孙克辉 艾星星 左婷 朱从旭

(1.中南大学物理与电子学院，长沙 410083)(2.新疆大学物理科学与技术学院，乌鲁木齐 830046)

引言

相比单涡卷和双涡卷混沌系统，多涡卷混沌系统具有更加复杂的动力学行为和更广泛的应用前景，因此，关于多涡卷混沌吸引子的研究正成为混沌领域的研究热点.国内外研究人员在该领域先后提出了用分段线性、阶梯波和符号函数等来产生多涡卷混沌吸引子的方法［1-7］.然而这些提出的非线性函数多为不连续的，存在突变点［1-12］.众所周知，混沌具有初值敏感性［13］，而函数的不连续和突变对混沌信号可能会造成一定的影响，物理实现也存在一定的困难.因此，研究采用连续的非线性函数产生多涡卷混沌吸引子具有重要研究意义.在非线性电路研究中，蔡氏电路是最早提出并且研究得最为透彻的一个混沌电路.Chua电路中，随着电路参数的变化，系统可呈现十分丰富的动力学行为，如倍周期分岔、单涡卷、周期、双涡卷等.由于Chua电路简单且容易实现，本文在Chua电路基础上，采用由连续函数双曲正切函数和线性函数叠加而成的非线性函数，研究基于连续非线性函数的多涡卷混沌吸引子设计方法及其动力学性能.

论文的安排如下，首先设计了两类连续的非线性函数，并将连续的非线性函数应用于Chua系统中，得到了单方向的多涡卷混沌吸引子，并对其进行了性能分析，讨论了系统参数的选取方法;然后设计了基于非线性函数的网格多涡卷混沌吸引子，并对网格多涡卷混沌系统进行了性能分析，最后给出结论.

1 基于Chua系统的单方向多涡卷混沌吸引子模型与性能分析

1.1 单方向多涡卷混沌吸引子的建模

多涡卷混沌系统的设计方法如下:选取适当的混沌系统并设计合适的非线性项，进行非线性项替代，并且使得在求平衡点的过程中能将平衡点计算简化为一元方程和一个线性方程组的求解.此方法的关键在于设计能产生多涡卷混沌吸引子的非线性函数，并注意调整平衡点的位置与类型.若设计的平衡点为指标2的鞍焦点则能产生涡卷，若为指标1的鞍焦点则能产生键带，设计的平衡点是指标1与指标2相间隔便能产生多涡卷混沌吸引子［5-7］.Chua系统微分方程为

其中α=10，β=16，h(x)是一个分段线性函数.

构造一个连续非线性函数替代原有的分段线性函数产生多涡卷吸引子，设计系统的非线性函数h(x)为

以上非线性函数h(x)是由线性的kx和非线性tanh(x)组合而成.因tanh(x)是连续的，连续函数相加减还是连续的，所以函数h(x)是连续的.k是线性项kx的斜率，p是非线性项的平移因子，可以控制产生涡卷的大小，p越大，吸引子范围越大.参数n的选取对非线性函数有较大的影响，n越大，tanh(nx)在各点的斜率越大，当n趋于无穷大时，tanh(nx)无限逼近符号函数.这里连续非线性函数是多涡卷混沌系统中产生多涡卷混沌吸引子的关键所在，tanh(x)函数波形如图1所示，当k=0.3，p=0.5，n=20时，以能产生六个涡卷为例，h(x)的波形如图2所示.

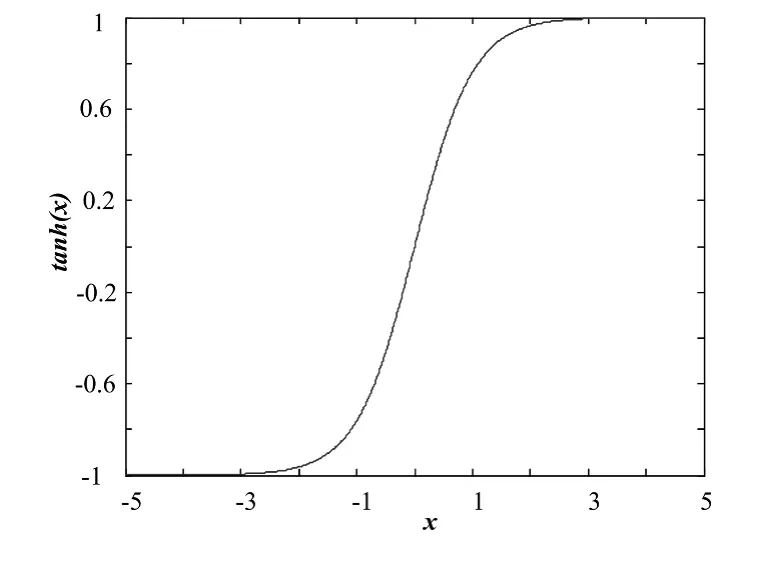
图1 tanh(x)函数波形Fig.1 Wave of tanh(x)

图2 非线性连续函数波形Fig.2 Wave of continuous nonlinear function

下面分析系统的平衡点特性，令式(1)左边等于零，得到平衡点方程组为h(x)=0，x+z=0，y=0.以两涡卷为例，则有x-0.5tanh(nx)=0，用一元不动点迭代法可求得x1=0.125，x2=-0.125，x3=0.系统在平衡点的Jacobian矩阵为

其中i=1，2，3.由此可得平衡点x1的3个特征值分别为-3.6228，0.2103±3.1116i.x2的3个特征值分别为-3.6228，0.2103±3.1116i.x3的3个特征值分别为27.3457，-0.6728±3.9173i.可见x1、x2平衡点为指标2的鞍焦点，可以形成涡卷，而x3平衡点为指标1的鞍焦点可以形成键带，通过键带将两个涡卷连接在一起，从而形成两涡卷吸引子.

1.2 单方向多涡卷混沌吸引子的数值仿真

取k=0.3，p=0.5，n=20，初始值为(0.3，0.1，0)，在Matlab中利用龙格-库塔法进行数值仿真，涡卷数目越多，呈现出完整吸引子的仿真时间越长，得单方向多涡卷吸引子相图如图3所示.

图3 单方向多涡卷吸引子相图(a)两涡卷(b)三涡卷(c)四涡卷(d)五涡卷(e)六涡卷(f)七涡卷Fig.3 Phase phase diagram of single direction multi-scroll attractors(a)two-scroll(b)three-scroll(c)four-scroll(d)five-scroll(e)six-scroll(f)seven-scroll

由图可知，利用连续的非线性函数可得到多涡卷混沌吸引子，并且系统是在x方向产生多涡卷吸引子，平衡点的分布位置是由连续非线性项所确定，得到吸引子清晰，大小一致，处于同一水平位置，y的取值范围一致，有利于电路实现，因为若每个吸引子的y范围太大，当涡卷数目太多时，会导致有些涡卷的y值会超出元器件的取值范围，不利于电路实现.

1.3 单方向多涡卷混沌吸引子的性能分析

这里以四涡卷吸引子为例，分析当系统参数变化时，系统的动力学特性.设p=0.5、n=20，参数k在［0，1］内变化，仿真步长为0.002，得到四涡卷吸引子随参数k变化的分岔图如图4所示.可见，纵坐标分为四个区域，这与四涡卷吸引子相图相对应;系统k参数在较大范围内处于混沌状态，对于保密通信应用而言，相应密钥范围空间大，可提高保密系统抗穷举攻击的能力.计算四涡卷吸引子关于参数k的最大Lyapunov指数曲线如图5所示，可见，最大Lyapunov指数在［0.072，0.826］范围内是正的，结果与图4所示的分岔图显示的范围相一致.此外，从图中可知，对于k参数而言，当k取0.3时吸引子大小和系统复杂性都比较合适.

图4 四涡卷吸引子关于参数k的分岔图Fig.4 Bifurcation diagram about k of four-scroll attractors

设k=0.3，n=20，参数p在［0.2，10］范围内变化，且仿真步长为0.002，四涡卷吸引子的关于参数p的分岔图如图6所示，可见参数p在该区域内系统是混沌的，p取0.5是正确的，而且随着参数p的增大，分岔图呈现持续增长的趋势，说明吸引子随p参数增加而变大，可见通过改变p的大小能够控制涡卷的大小，这对多涡卷混沌系统的应用具有实际意义.同样，计算四涡卷吸引子关于参数p的最大Lyapunov指数如图7所示.可见，系统在［0.2，10］范围内最大Lyapunov指数为正，表明系统在该范围内处于混沌状态，与分岔图6相一致，尽管在p=2.79附近，系统最大Lyapunov指数出现极小值，但其值仍然为正，所以此时附近系统也是处于混沌状态.

图5 系统最大Lyapunov指数随参数k变化的波形Fig.5 Largest Lyapunov exponent about k of system

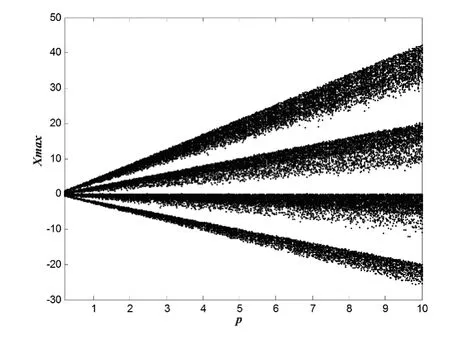
图6 四涡卷吸引子关于参数p的分岔图Fig.6 Bifurcation diagram about p of four-scroll attractors

图7 最大Lyapunov指数随参数p变化的波形Fig.7 Largest Lyapunov exponent about p of system

设k=0.3，p=0.5，参数n在［3，25］范围内变化，且仿真步长为0.005，四涡卷吸引子的关于参数n的分岔图如图8所示，为了能够清楚的观察其分岔行为，将区间［3，5］放大可得图9，可见系统是以倍周期分岔方式进入混沌.同样，计算四涡卷吸引子关于参数n的最大Lyapunov指数如图10所示.可见，系统在［3.66，25］范围内最大Lyapunov指数为正，表明系统在该范围内处于混沌状态，与分岔图8相一致.而且随着参数n的变化，系统可呈现极限环、周期、混沌等动力学状态，如图11示.

图8 四涡卷吸引子关于参数n的分岔图Fig.8 Bifurcation diagram about n of four-scroll

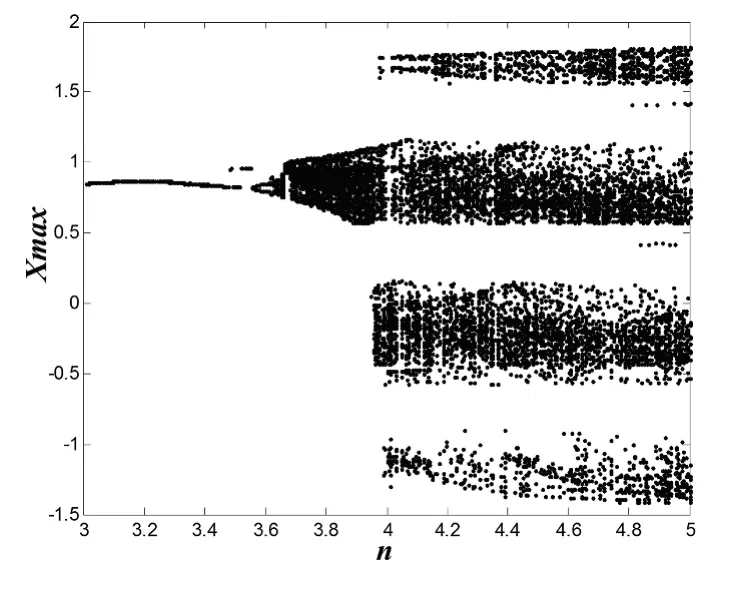
图9 区间放大后的分岔图Fig.9 Bifurcation diagram of region expinson

图10 最大Lyapunov指数随参数n变化的波形Fig.10 The largest Lyapunov exponent about n

为了更好地验证系统的混沌特性，计算y=0.01为截面的四涡卷混沌吸引子的Poincaré截面如图12示，截面上是一些成片的密集点，说明系统是混沌的，并且主要密集地分布在四条并行的线上，说明系统处于四涡卷混沌吸引子状态，截面上分散的点，说明涡卷之间通过键带连接.

图11 参数n变化时的吸引子相图Fig.11 Phase diagrams with different n

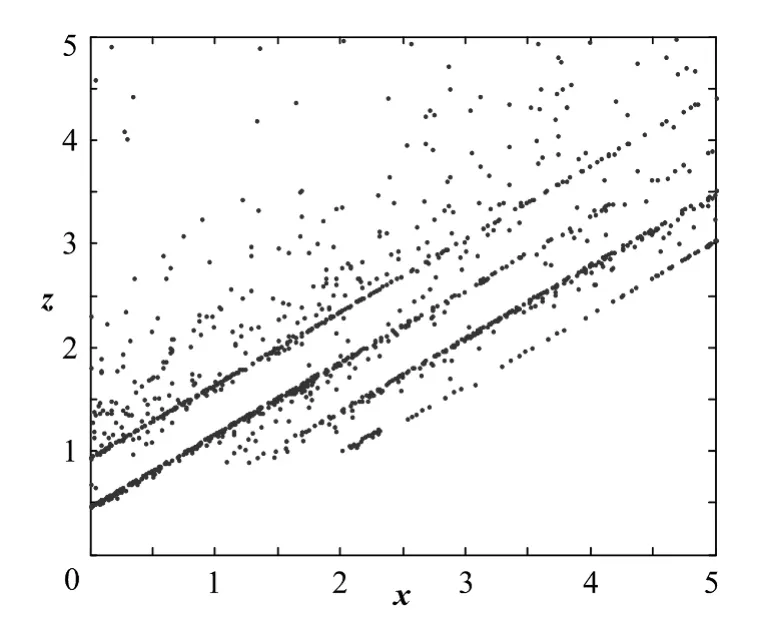
图12 四涡卷混沌吸引子的Poincaré截面图Fig.12 Poincarésection of four-scroll chaotic attractor

2 基于Chua系统的网格多涡卷吸引子的建模与仿真

2.1 网格多涡卷吸引子的建模

网格多涡卷混沌吸引子在不同的方向上同时产生多涡卷，具有更为复杂的拓扑结构.为了设计网格多涡卷混沌吸引子，在y方向上引入一个非线性项，其微分方程为

式中，α=10，β=16，h(x)控制x方向的涡卷数目，f(y)控制y方向涡卷的数目.

以上函数中，k是线性项kx的斜率，p是非线性项的平移因子，能够控制产生涡卷的大小，p越大，吸引子范围越大，q为比例因子，控制y方向平衡点的位置.设k=0.5，p=0.25，q=0.25，n=20，以5×4网格多涡卷混沌吸引子的平衡点为例，可得x-y相平面上鞍焦点分布如图13所示，图中符号“○”表示平衡点为指标2的鞍焦点，可产生涡卷.

图13 5×4网格多涡卷吸引子的鞍焦点分布Fig.13 Saddle-focus distribution of grid 5×4 multi-scroll attractor

2.2 网格多涡卷混沌吸引子的数值仿真

取k=0.5，p=0.25，q=0.25，n=20，取初始值为(0.3，0.1，0)，采用龙格库塔法进行数值计算，得到的吸引子相图如图14所示.

图14 Chua网格多涡卷混沌吸引子(a)2×2多涡卷(b)2×3多涡卷(c)3×3多涡卷(d)3×5多涡卷(e)5×4多涡卷(f)6×5多涡卷Fig.14 Saddle-focus distribution of grid 5×4 multi-scroll attractor(a)2×2multi-scroll(b)2×3 multi-scroll(c)3×3 multi-scroll(d)3×5 multi-scroll(e)5×4 multi-scroll(f)6×5 multi-scroll

由图可知，利用连续的非线性函数能够得到网格多涡卷混沌吸引子，平衡点的分布位置是由连续非线性项所确定，得到的吸引子清晰，大小一致，而且通过改变非线性函数可以得到任意数目的多涡卷混沌吸引子.

2.3 网格多涡卷混沌吸引子的性能分析

以2×2网格多涡卷吸引子为例，分析系统参数变化时，系统的动力学特性，仿真步长均为0.002.1)设p=0.25，q=0.25，n=20，参数k在［0，2］内变化，计算2×2网格多涡卷吸引子关于参数k的最大Lyapunov指数曲线如图15(a)所示.可见，最大Lyapunov指数在［0.146，1.736］范围内是正的，表明该范围内系统处于混沌态.2)设k=0.5，q=0.25，n=20，参数p变化，且p∈［0，4］，计算2×2网格多涡卷吸引子关于参数p的最大Lyapunov指数曲线如图15(b)所示.可见，最大Lyapunov指数在［0，0.644］和［2.262，4］范围内是正的，表明在该范围内系统处于混沌态，但在区间［0.664，2.262］存在周期态窗口.3)k=0.3，p=0.25，n=20，参数q变化，且q∈［0，2］，计算2×2网格多涡卷吸引子关于参数q的最大Lyapunov指数曲线如图15(c)所示，可见，最大Lyapunov指数在［0，0.51］和［0.766，0.95］范围内都是正的，表明在该范围内系统处于混沌态，且在区间［0.51，0.766］和［0.95，2］存在周期态窗口.4)设k=0.5，p=0.25，q=0.25，参数n在［0，25］内变化，计算2×2网格多涡卷吸引子关于参数n的最大Lyapunov指数曲线如图15(d)所示.可见，最大Lyapunov指数在［0，25］范围内是正的，表明在该范围内系统处于混沌态.

图15 2×2多涡卷系统的最大Lyapunov指数Fig.15 Largest Lyapunov exponent of 2×2 multi-scroll system(a)parameter of k(b)parameter of p(c)parameter of q(d)parameter of n

为了更好地验证系统的混沌特性，计算z=-0.5为截面的2×2网格多涡卷吸引子Poincaré截面图如图16所示，截面上是一些成片的密集点，表明系统是混沌的，并且主要密集地分布在四块区域，说明系统是处于2×2网格多涡卷吸引子的状态.

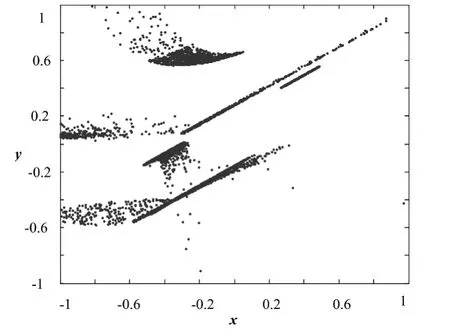
图16 2×2多涡卷混沌吸引子的Poincaré截面图Fig.16 Poincarésection of 2×2 multi-scroll chaotic attractor

3 结论

本文研究了基于连续非线性函数的Chua系统多涡卷混沌系统的建模、仿真与动力学特性问题，通过构造连续的非线性函数，在Chua系统中得到了单方向与网格的多涡卷混沌吸引子，得到的多涡卷混沌吸引子相图清晰、涡卷大小相同.讨论了系统参数对多涡卷吸引子及其性能的影响，为正确选取系统参数提供了实验依据.研究表明，基于连续非线性函数的Chua多涡卷吸引子具有丰富的动力学特性，多涡卷混沌系统的理论分析和数值分析得到的结果相一致，说明多涡卷混沌吸引子设计方法可行.下一步将研究多涡卷吸引子的电路实现及其应用.

1 禹思敏.用三角波序列产生三维多涡卷混沌吸引子的电路实验.物理学报，2005，54(04):1500～1509(Yu S M.Circuit implementation for generating three dimensional multi-scroll chaotic attractors via triangular wave series.Acta Physica Sinica，2005，54(04):1500～1509(in Chinese))

2 刘明华，禹思敏.多涡卷高阶广义Jerk电路.物理学报，2006，55(11):5707～5713(Liu M H，Yu S M.Multi-scroll Jerk circuits.Acta Physica Sinica，2006，55(11):5707～5713(in Chinese))

3 张朝霞，禹思敏.用时滞和阶跃序列组合生成网格多涡卷蔡氏混沌吸引子.物理学报，2009，58(1):120～130(Zhang Z X，Yu SM.Combination of hysteresis and step sequences generated grid multi-scroll Chua chaotic to attract sub.Acta Physica Sinica，2009，58(1):120～130(in Chinese))

4 王发强，刘崇新.一类多折叠环面多涡卷混沌吸引子的仿真研究.物理学报，2007，56(04):1983～1987(Wang F Q，Liu CX.Simulation of a family of multi-folded torus and multi-scrolI chaotic attractors.Acta Physica Sinica，2007，56(4):1983～1987(in Chinese))

5 谌龙，彭海军，王德石.一类多涡卷混沌系统构造方法研究.物理学报，2008，57(06):3337～3341(Chen L，Peng H J，Wang D S.Studies on the construction method of a family of multi-scroll chaotic systems.Journal of Physics，2008，57(6):3337～3341(in Chinese))

6 包伯成，徐强，徐煜明等.三维多涡卷Colpitts混沌系统及其数字硬件实现.电路与系统学报，2011，16(1):69～73(Bao B C，Xu Q，Xu Y M，et al.Three-dimensional multi-scroll coipitts chaotic system and its digital hardware implementation.Journal of Circuits and Systems，2011，16(1):69～73(in Chinese))

7 Mustafa T，Hidayet O.Recognition of multi-scroll chaotic attractors using wavelet-based neural network and performance comparison of wavelet families.Expert Systems with Applications，2010，37:8667～8672

8 Yu SM，LüJ H，Chen G R.A family of n-scroll hyperchaotic attractors and their realization.Physics Letters A，2007，364:244～251

9 Sanchez L C.Automatic synthesis of chaotic attractors.Applied Mathematics and Computation，2011，217(9):4350～4358

10 Xu F，Yu P.Chaos control and chaos synchronization for multi-scroll chaotic attractors generated using hyperbolic functions.Mathematical Analysis and Applications，2010，362:252～274

11 Li G L，Chen X Y.Constructing piecewise linear chaotic system based on the heteroclinic Shil’nikov theorem.Communications in Nonlinear Science and Numerical Simulation，2009，14:194～203

12 Liu C X，Yi J，Xi X C，An L M，Qian Y，Research on the multi-scroll chaos generation based on Jerk mode.Procedia Engineering，2012，29:957～961

13 李清都，杨晓松.基于拓扑马蹄的混沌动力学研究进展.动力学与控制学报，2012，10(4):293～299(Li Q D，Yang X S.Progresses on chaotic dynamics study with topological horseshoes.Journal of Dynamics and Control，2012，10(4):293～299(in Chinese))