分数阶复杂网络的混合投影同步研究*

杨丽新 江俊

(西安交通大学强度与振动国家重点实验室，西安 710049)

引言

自从复杂网络的小世界特性和无标度特性被发现以来［1-2］，复杂网络就吸引了大量自然科学和工程应用领域方面的科研人员关注［3-4］.其主要原因是复杂网络已经广泛应用于实际生活中，例如经济系统、因特网、生物神经网络以及大型机器人系统等.复杂网络的应用，不仅简化了系统的控制方法，而且节省了大量的能源和经费，作为复杂网络的一个重要动态特性，同步已经得到了广泛的研究，并且存在着大量的复杂网络同步结果.过去十几年，许多关于混沌同步的控制方法已被提出，文献［5］研究了复杂网络的带有耦合延迟的全局同步，接着，文献［6］基于牵引控制，讨论了一类较为一般的复杂网络系统的同步问题，提出了一种简化近似公式来估计牵制结点个数和未知的耦合强度等.

然而，研究复杂网络的同步成果，考虑的节点大多数为整数阶导数，近几年来，分数阶微积分的应用领域越来越广泛，分数阶模型更加准确地刻画实际系统的物理现象，2010年，房建安等研究了加权网络的牵引控制问题［7］，给出了分数阶动力学网络的控制性能与分数阶次，以及耦合强度的关系，随后，很多学者研究了复杂网络的同步问题［8］.然而，分数阶复杂网络的同步控制问题还处于起步和探索阶段，有许多问题值得去研究.

本文基于分数阶系统的稳定性理论，主要讨论分数阶混沌动力学网络的混合投影同步控制问题，给出了一类具有不同节点的分数阶混沌动力学模型，为使得该类网络达到混合投影同步，设计了非线性控制器，并得到了实现同步的充分条件，数值仿真结果进一步验证了所提方法的有效性.

1 准备知识和问题描述

目前为止，已经有多种分数阶微分的定义，常用的是Riemann–Liouvile和Caputo定义，由于后者更适合描述分数阶微分方程的初值问题，因此，本文采用Caputo定义，简单描述如下

其中Γ(·)表示Gamma函数.

考虑一般的分数阶线性微分方程［9］

其中X∈Rn，A∈Rn×n，0＜q≤1.

对于线性分数阶系统(2)，若|arg(λi(A))|＞qπ/2成立，则分数阶系统(2)渐近稳定.

我们考虑含有N个节点的分数阶动力学网络如下:

其中q∈(0，1］;xi(t)=(xi1(t)，xi2(t)，…，xin(t))T∈Rn分别表示第i个节点动力学系统的阶数和状态变量，Fi:Rn→Rn是非线性连续函数，用来描述第i个节点的动力学行为，Γ是内部耦合矩阵，C=(cij)N×N∈RN∈N是外部耦合矩阵，表示网络的拓扑结构和耦合强度，矩阵元素cij定义如下:如果节点i和节点j之间有边连接且(i≠j)，则cij＞0，否则，cij=0(i≠j)，矩阵C的对角元素定义如下:

假设复杂网络的孤立节点的解满足下式:

其中G:Rn→Rn是非线性光滑函数.s(t)可以是一个稳定点，或者周期解，也可以是混沌轨迹.

定义1 对于给定的分数阶复杂网络(3)，若存在一个非零矩阵Λ，使得Λs(t)‖=0，i=1，2，…，N成立，即复杂网络实现了混合投影同步，其中，Λ=diag(λ1，λ2，…，λn)称为标度矩阵，λi表示标度因子.

假设1 假设存在正的常值L，满足不等式‖f(y)-f(x)‖≤L‖y-x‖，其中x和y是时变向量.

2 主要结果

我们考虑如下受控的分数阶复杂网络

其中，ui(t)∈Rn(i=1，2，…，N)是待设计的非线性控制器.

为了设计控制器的方便，我们可把目标节点和分数阶网络系统重新写成如下形式

式中，Ai，B∈Rn×n，g(s(t))和fi(xi(t))分别是参考轨迹和第i个节点动力学系统的的非线性部分.

定义误差向量

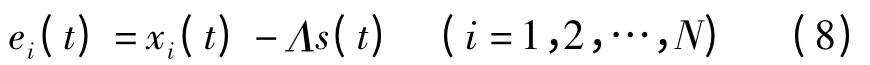
我们可以得到具体的误差动力学系统如下:

我们的目标是设计合适的控制器ui(t)，使得误差系统在原点稳定.为此，我们设计如下的控制器，以定理形式给出.

定理1 对于给定的标度矩阵Λ和初值条件xi(0)，s(0)，若设计如下的控制器

式中，Λ=diag(λ1，λ2，…，λn)是标度矩阵，ki是正的反馈增益，则分数阶网络(7)可以实现混合投影同步.

证明:根据误差向量的定义

把控制器(10)式代入(9)式，得到下式:

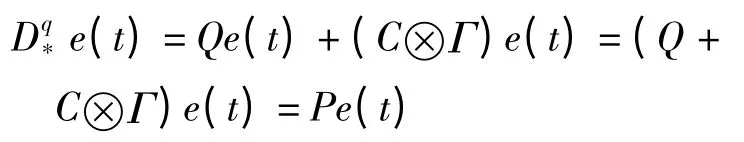
式中，Q=diag(Ai-kiIn)(i=1，2，…，N)

只要我们选取合适的反馈增益ki，使得矩阵P的任意特征值满足成立，根据分数阶系统的稳定性定理，则可以实现分数阶网络的混合投影同步.

3 数值仿真

我们选分数阶超混沌Chen系统为网络目标节点:

当q=0.98，a=35，b=3，c=12，d=7，r=0.5，系统(12)呈现超混沌吸引子，如图1所示.

图1 分数阶超混沌Chen系统的吸引子Fig.1 The attractor of Chen fractional-order hyper-chaotic system

下面考虑一10个节点的分数阶复杂网络，前5个节点为一个新的超混沌分数阶系统，动力学方程为:

参数取值为q=0.98，e=10，f=15，h=40，θ=10，d=2.5，系统(13)产生超混沌吸引子，如图2所示.

图2 分数阶超混沌新系统的吸引子Fig.2 The attractor of the new fractional-order hyper-chaotic system

其余5个节点为分数阶超混沌Lorenz系统，如下描述

当参数取值为q=0.98，(a，b，c，r)=(10，8/3，28，-1)，系统(14)超混沌状态.

我们考虑10个节点的网络，则具有不同节点的分数阶动学网络可以表示为下式:

图3 分数阶超混沌Lorenz系统的混沌吸引子Fig.3 The attractor of Lorenz fractional-order system

图4 同步误差随时间的变化历程，当标度矩阵为Λ=diag(-1，1，1.-2)Fig.4 Time evolution of synchronization errors E(t)with scaling matrixΛ=diag(-1，1，1.-2)

为了数值仿真的简单起间，选取内部耦合矩阵为Γ=I4，外部耦合矩阵任意选取为

定义eij(t)=xij(t)-Λjsj(t)(i=1，2，…，N;j=1，2，3，4)，则网络系统状态变量均方误差:

状态变量的初始值分别选取在区间(-5，5)间任意选取，选取标度矩阵为对角阵，元素分别为λ1=-1，λ2=1，λ3=1，λ4=-2，为了方便，我们固定阶数q=0.98，得误差随时间演化如图4所示:

4 结论

研究了分数阶复杂网络系统的混合投影同步问题，我们所讨论的分数阶复杂网络有更广泛的形式，即内部和外部耦合矩阵都不必要满足对角和可约简的条件，同时以分数阶混沌系统的稳定性理论为基础，设计合适的非线性控制器，实现了不同节点的分数阶复杂网络的混合投影同步，数值仿真进一步的说明了此方法的有效性.

1 Watts D J，Strogatz SH.Collective dnamics of small-world networks.Nature，1998，393(6684):440～442

2 Barabasi A L，Albert R.Emerging of scaling in random network.Science，1992，286:509～512

3 张刚，张伟.复杂网络的脉冲同步.动力学与控制学报，2009，7(1):1～4(Zhang G，Zhang W.Impulsive synchronization of complex networks.Journal of Dynamics and Control，2009，7(1):1～4(in Chinese)

4 尚磊，郑永爱.输出耦合的复杂网络自适应脉冲同步.动力学与控制学报，2012，10(1):48～51(Shang L，Zheng Y A.Adaptive impulsive synchronization of complex networks coupled with the outputs.Journal of Dynamics and Control，2012，10(1):48～51(in Chinese)

5 Sun W，Chen SH，Guo WL.Adaptive global synchronization of a general complex dynamical network with non-delayed and delayed coupling.Physics Letters A，2008，372:6340～6346

6 Tang Y，Wang Z，Fang J.Pinning control of fractional-order weighted complex networks.Chaos，2009，19(1):1311～1321

7 Tang Y，Fang J.Synchronization of N-coupled fractionalorder chaotic systems with ring connection.Communication in Nonlinear Science and Numerical Simulation，2010(2)，15:401～412

8 Duan Z S，Chen G R，Huang L.Synchronization of weighted networks and complex synchronized regions.Physics Letters A，2008，372(21):3741～3751

9 Matignon D.Stability results for fractional differential equations with applications to control processing，In:Computational engineering in systems and application multi-conference.Lille:IMACS，IEEE-SMC Proceedings，1996，2:963～968