预变形对非线性结构响应特征的影响*

王珺 赵环迪 陈力奋

(复旦大学力学与工程科学系，上海 200433)

引言

局部非线性在许多复杂机械和工程结构中都存在，通常位于部件的结合处，例如轴承［1，2］、套管［3］、齿轮［2，4］等.关于局部非线性的理论研究方法，姚红良等［5］做出了突出的贡献.然而实际情况中，整个系统尤其是非线性元件除了受动态激励外，还常常受到其它载荷，如重力、装配缺陷等引起的预载等.这些载荷大小的变化会改变系统的静平衡点，进一步影响非线性元件的动态特性.例如，在零静载时对称的非线性弹簧，在预载荷作用下会成为非对称［6］，由此使得一些适用于处理对称非线性的方法，例如描述函数［7］等不再适用.与此同时，外激励的类型和幅值也多种多样，导致非线性结构表现出非常复杂的响应特征.

已经有一些学者对存在预载和复杂外激励的非线性系统进行了理论和实验研究，典型的是一种T字型的梁结构，最初由Ferreira［8］采用，此后Siller［9］和Ozge［10］等也将其应用于各自的研究.研究表明，当响应位移较大时，实验中的装配缺陷会对非线性系统响应有明显的影响，包括缝隙，预变形等.例如，存在预变形的立方刚度弹簧会表现得像一个不对称的软弹簧［8］;这些研究初步揭示了带预变形非线性系统复杂的响应特征，但没有关注在不同的外激励和预变形下非线性结构响应特征的变化过程.

本文在与实验结合的基础上，进行了仿真分析.在仿真计算过程中，通过自动判断稳定性、递归细分和并行计算，极大地减少了计算时间.仿真结果表明，不同参数下的非线性系统存在丰富的非线性现象，预变形和外激励幅值对系统的非线性特征影响显著，进一步揭示了在不同的外激励和预变形下非线性结构响应特征的演变过程.

1 实验梁的非线性频响特征

本文采用文献［8-10］中的T字型结构进行实验研究，实验试件和激振器如图1a所示.其中，矩形截面主梁尺寸1000×12×8，二个横梁尺寸500×13×1.42(单位:mm);材料常数E=2.1×1011Pa，ρ=7.8×103kg/m3.外激励下横梁的大变形使得主梁的一端受到非线性约束支撑.实验装置搭建过程中，由于重力、装配误差等因素的影响，使得T字型梁成为一个带预变形的非线性结构，如图1b所示.

图2为改变外激励幅值的大小，进行恒力控制下从低到高的单向扫频实验结果.

图3为当外激励幅值逐渐从增大到时，分别从高频到低频(黄色)、再从低频到高频(其他颜色)扫频，测量到的离端点250mm处的位移响应.

图1 T字型梁结构的实验装置Fig.1 The experiment equipment of the T–beam structure

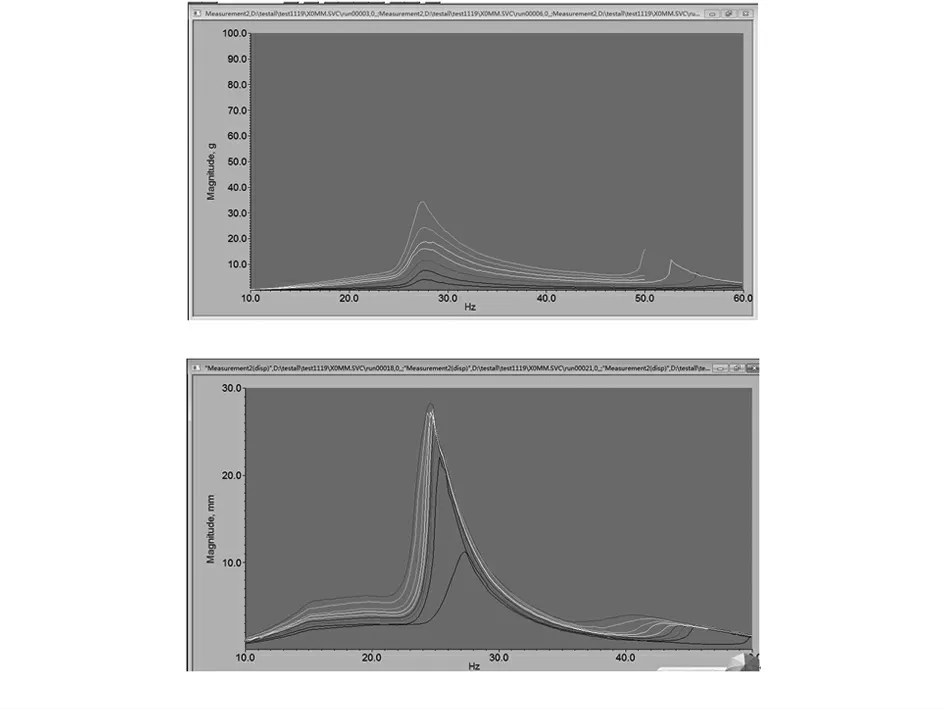
图2 恒力控制下端点处自频响应的实验结果Fig.2 The experimental results of the self-excited response under constant force amplitude

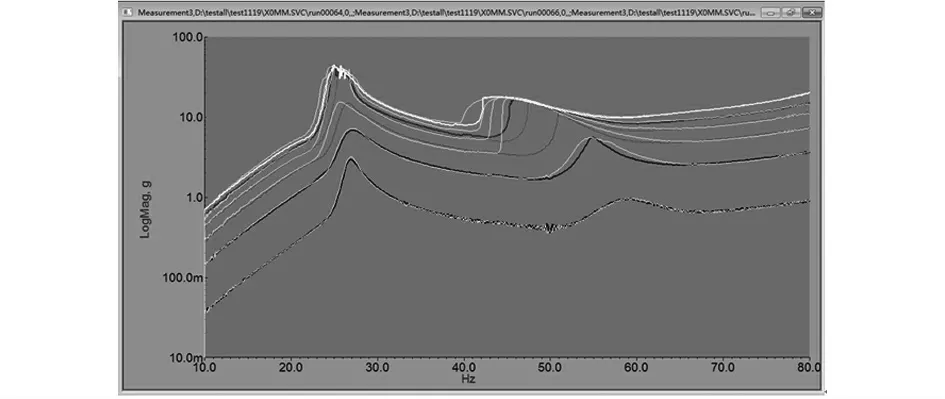
图3 离端点250mm处的位移响应Fig.3 The displacement response 250mm away from the beam’s end

2 含预变形非线性结构的理论与计算

对于带预变形的T字型梁，从图2中可以看出，存在着明显的软特性.而在图3中不难发现，当外激励幅值较小(如0.4N)时就已经出现跳跃现象.为此，本文接下来对含预变形的非线性结构进行理论和数值的仿真分析.

2.1 基本理论

考虑图4所示的单自由度质量—阻尼—弹簧系统，其中大变形产生的非线性弹簧同时具有线性和立方刚度，即弹簧的变形x(取弹簧自然伸长时为x=0)与弹簧对m的作用力F存在如下关系:

式中，k为线性刚度系数，k*为立方刚度系数;负号则表示结构受到的弹簧力方向与位移方向相反.

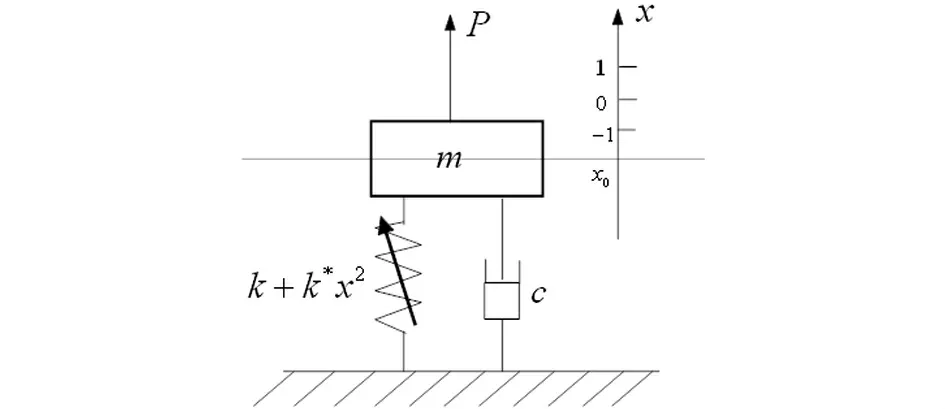
图4 含非线性弹簧的单自由度质量-阻尼-弹簧系统Fig.4 A mass-damp-string system of one dimension with a nonlinear string

若因为重力等原因，系统静平衡状态时弹簧存在一个预变形x0，则此时弹簧对m的作用力为:

当m相对静平衡位置有一个位移Δx，弹簧对m作用力的增量为:

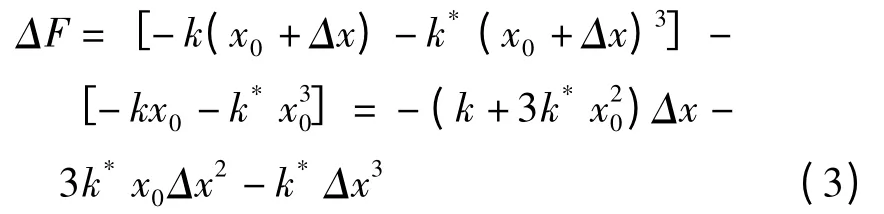
不难发现，式(3)中线性项的系数是随x0变化的.如果m受到的其它作用力(如重力)不会因为Δx的产生而有任何改变，则上式即是m受到的合力.于是系统在外激励P作用下的运动微分方程为:

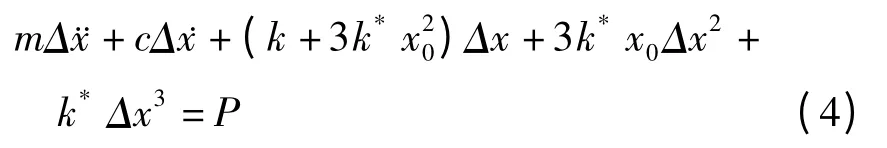
由于Δx的一次项系数随着x0而变化，系统理论上的线性频率表达式为:

显然，也与预变形x0相关.

对于式(4)可以作如下简要分析:

1.当Δx为小量时，二次项和三次项相对于一次项可以忽略，系统主要表现线性行为;随着Δx的增大，二次项影响逐渐显著;Δx继续增大，三次项开始占据主导地位.

2.当x0=0时，系统只存在三次项的非线性;随着x0的增大，二次项开始体现作用.x0继续增大，则非线性项相对线性项越来越不重要，系统又呈线性特征.

因此，对于这样一个同时存在平方和立方非线性的模型，随着预变形x0和外激励幅值F的变化，将会出现跳跃、超谐波共振、次谐波共振等丰富的非线性现象.

2.2 计算方法的改进

为模拟扫频实验中从低频到高频，以及从高频到低频的实验过程，本文在matlab计算平台上进行了仿真计算，主要步骤有:

1)采用经典的5阶定步长龙格-库塔法，计算系统在某一初始条件、一定预变形和恒力幅值简谐外激励作用下的响应.

2)待系统稳定后，截取一段时域响应进行傅利叶变换;考虑到弱非线性时的主频响应占主导，以及与扫频实验相匹配，取幅值最大的一个频率作为主频响应，并以这个幅值与激励力幅值之比作为拟线性的频响.

3)为模拟实验时的扫频，初始频率点时以位移和速度均为0作为初始条件，此后的频率点均以系统在上一个频率点(已达到稳定)最后时刻的运动状态(位移和速度)作为初始条件;参照实验进行从低到高和从高到低改变外激励频率的大小，并比较计算结果.

龙格-库塔法计算时域响应时，关键在于如何判断系统是否达到稳定，是第2步计算的前提，也是最主要的计算耗费所在.文献［11］中对任意参数都采用固定的计算周期数.事实上，系统在不同频率点达到稳定需要的时间是很不一致的;一般地，在初始点(零初始条件，而其它点是一个较接近稳态的初始条件)和突变点需要较长的时间，而在曲线光滑的位置只需要很短的时间就能达到稳定;在一些特殊的点比如次谐波共振点则需要非常长的时间.文献［11］采用固定周期数的方法，在大部分点上浪费计算时间，而在某些点处又不能真实地反映稳态情况.针对上述情形，本文在计算中采用了自动判断稳定性的方法，基本思想是:以外激励周期截取系统时域响应，比较邻近几段的差异，以此来判断系统是否达到稳定.由此，在曲线的光滑点可以极大地减少计算时间;而对长时间不收敛的参数点则可认为是可能的特殊点.

为了进一步减少计算量，在扫频范围内首先采用较大的初始频率间隔进行扫频计算，当发现频响曲线出现“异常”，即斜率的绝对值变化很大或者斜率的正负号改变(峰值或谷值)时，进行递归细分，直到斜率变化平缓或细分到设定的下限值.由此，既准确地描述了频响曲线的整体形状和关键位置细节信息，又大大加快了计算速度.

此外，由于不同物理参数(预变形和外激励幅值)取值的频响曲线计算时，相互之间没有影响，因此，本文在matlab计算平台上采用并行计算，又一次极大地节约了计算时间.

随着高等教育的不断改革，高校也更注重对学生综合素质的培养。而实验课的教学是高校对学生综合素质培养必不可少的课程之一，现如今各个高校均配有实验室，对实验设备要求也越来越高，都希望采购先进的实验仪器设备来让学生进行体验。而学生通过一次次的实验能够深刻地了解理论知识，锻炼自己的动手能力，也能够通过实验进行创新，所以实验教学仪器在实验教学中发挥着重要作用。也可以说没有实验仪器的实验课程是无法开展的。

综上所述，本文在仿真计算过程中，通过自动判断稳定性、递归细分和并行计算，极大地减少了计算时间.

2.3 参数设置

仿真计算中物理参数的取值，是以T字型梁的静力学和扫频实验测得的数据为基础的.图5a为T字型梁的静力学实验所测得的力和位移关系曲线，图5b是外激励幅值为F=0.025N时的恒力扫频实验结果曲线.按照(3)式将图5a中的实验数据进行非线性拟合，求出线性刚度系数k=3.4324N/mm和立方刚度系数k*=0.1533N/mm3.根据k和图5b的线性扫频实验得到的一阶固有频率，取定等效质量m=0.1kg.

图5 确定T字型梁物理参数的实验结果ig.5 The experimental results to identify the physical parameters of the T-beam

3 仿真结果的非线性现象分析

在计算结果中，对任意4个外激励频率相邻的数据点(fi，xi)，i=1，2，3，4，(f1＜f2＜f3＜f4)，其中xi为对应于频率fi激励下的响应，令:

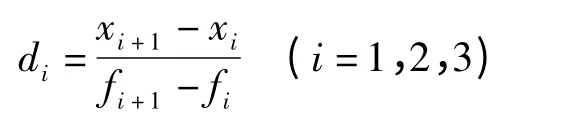
计算结果中，当|d2|＞n|d1|且|d2|＞n|d3|时，其中n为给定的常数，定义频率点:

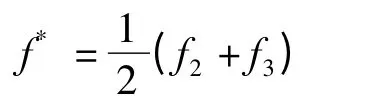
处为一个跳跃点，d2为f*处的斜率，本文分析中取n=2.通过计算结果中跳跃点的筛选，能有效地反映频响曲线跳跃的位置.

3.1 硬化和软化的跳跃

对于不同的预变形和激励力幅值的取值，系统表现出了硬化和软化的跳跃现象.

图6是固定激励力幅值F=10N时，跳跃点f*位置随预变形的变化，图7是此时几条典型的频响曲线.从图中可以清晰地看出，随着预变形的增大，系统由硬化逐渐过渡到软化，临界点在大约x0=5mm处;最终跳跃消失，呈线性特征.这与理论分析完全符合.

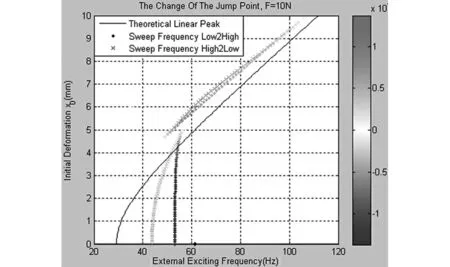
图6 跳跃点位置随预变形的变化Fig.6 The change of the jump point in terms of the initial deformation

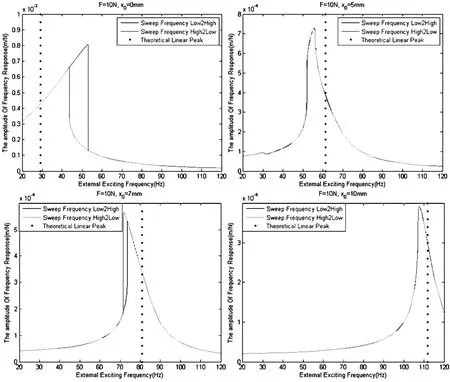
图7 F=10N时几条典型的频响曲线Fig.7 Some typical frequency response curve while F=10N

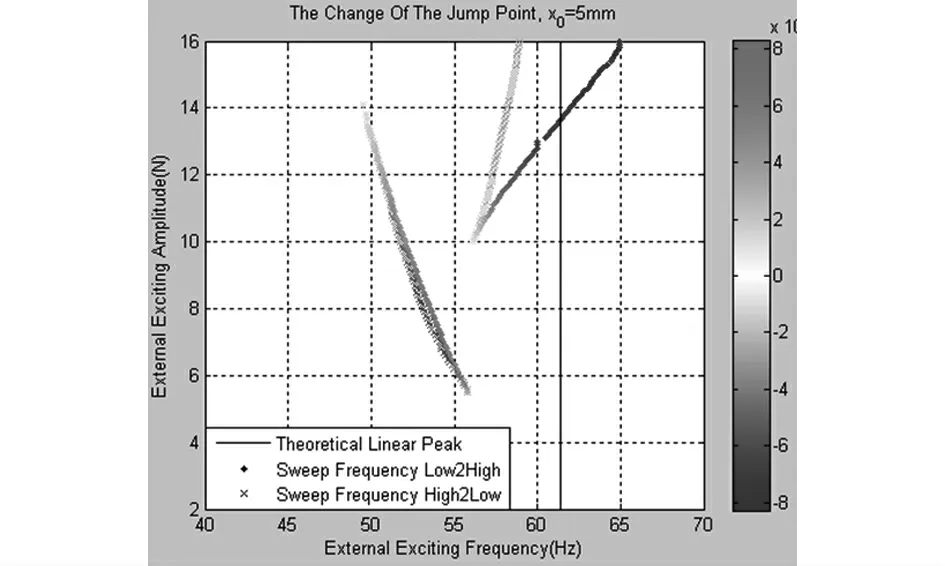
图8 跳跃点位置随外激励幅值的变化Fig.8 The change of the jump point in terms of the external exciting amplitude

(颜色表示跳跃点的斜率，其中从高到低扫频时的斜率为通常意义下斜率的相反数)

图8是固定预变形x0=5mm时，跳跃点位置随激励力幅值的变化.图9是此时几条典型的频响曲线.由图中可以看出，随着激励力幅值的增大，系统由线性逐渐过渡到软化，最终呈现硬化.考虑到本模型中各项系数均为正，则激励力幅值与系统响应幅值呈单调关系，这些结果也与理论完全符合.

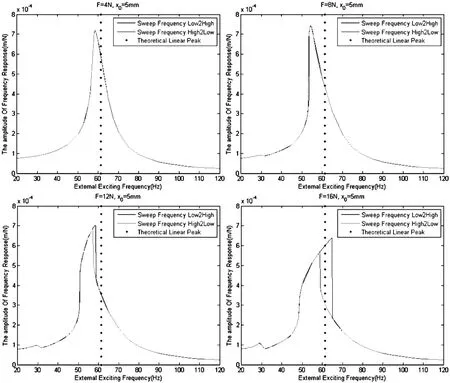
图9 x0=5mm时几条典型的频响曲线Fig.9 Some typical frequency response curve while x0=5mm

3.2 超谐波共振

图10是固定激励力幅值F=10N时，峰值位置随预变形的变化.由图中可以看出，左端的峰值正好对应于约线性固有频率1/2处的超谐波共振，这是平方非线性的特征，随着预变形的增大最终消失;两种扫频方式在此处是完全重合的.而两种扫频方式的主共振峰值相对位置的变化也体现了系统硬化→软化→线性的变化.

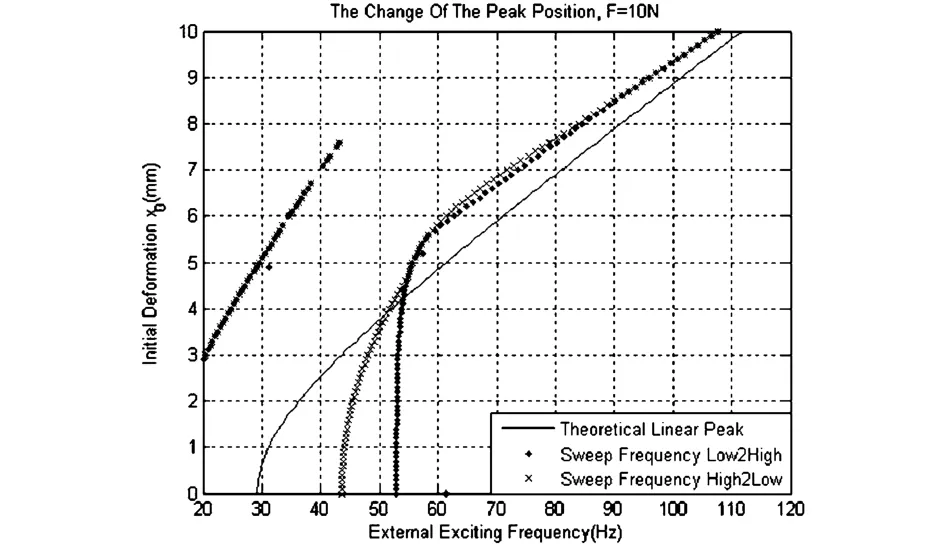
图10 峰值位置随预变形的变化Fig.10 The change of the peak position in terms of the initial deformation

图11是固定预变形x0=5.1mm时，峰值位置随激励力幅值的变化.左上角的峰值对应于线性固有频率1/3处的超谐波共振，这是立方非线性的特征，在激励力幅值比较大时才开始出现;两种扫频方式在此处也是完全重合的.

图11 峰值位置随外激励幅值的变化Fig.11 The change of the peak position in terms of the external exciting amplitude

3.3 次谐波共振

计算过程中通过观察时域收敛的情况，发现当预变形x0=1.8～2.6mm，外激励幅值超过临界值F*≈15N时，固有频率2倍处出现了次谐波共振的现象，如图12所示.这一现象与文献［11］中的理论预测相符.另一方面，次谐波共振随着x0的增加从无到有再消失的变化过程，也体现了二次项的影响逐渐增大再减小的变化过程.

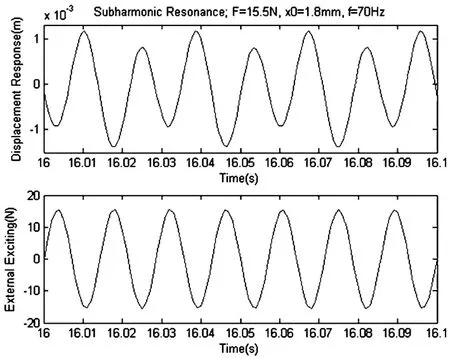
图12 次谐波共振示例Fig.12 An example of subharmonic resonance

(所取参数下，系统线性固有频率为35.31Hz，约为外激励频率70Hz的一半左右)

4 结论

本文在实验研究的基础上，通过建立单自由度仿真模型，数值求解过程中通过计算方法的改进，极大地减少了计算量，成功地对存在预变形的立方刚度非线性进行了仿真.随着预变形和激励力幅值的变化，观察到了丰富的时域和频域的非线性响应现象，并揭示了其变化的过程，得到了与理论推测相符的结果.进一步需要研究的问题是如何更有效地提高计算速度，以更完整地体现非线性现象;并扩展到多自由度系统，直至模拟连续系统(如梁)的非线性效应.可以预见，多自由度系统将出现内共振等更加丰富的非线性现象，但也对程序和算法的优化提出了严峻的挑战.

1 Kim Y B，Noah ST，Choi Y S.Periodic response of multidisk rotors with bearing clearances.Journal of Sound and Vibration，1991，144(3):381～395

2 Kahraman A，Singh R.Non-linear dynamics of a geared rotor-bearing system with multiple clearances.Journal of Sound and Vibration，1991，144(3):469～506

3 Bindemann A C，Ferri A A.Large amplitude vibration of a beam restrained by a non-linear sleeve joint.Journal of Sound and Vibration，1995，184(1):19～34

4 Padmanabhan C，Singh R.Spectral coupling issues in a two-degree-of-freedom system with clearance nonlinearities.Journal of Sound and Vibration，1992，155(2):209～230

5 姚红良，韩清凯，冯霏等.多自由度局部非线性系统频域响应及非线性位置的辨识方法.动力学与控制学报，2011，9(2):107～110(Yao H L，Han Q K，Feng F，et al.NOFRF of the locally nonlinear MDOF system and the detection method of the nonlinearity position.Journal of Dynamics and Control，2011，9(2):107～110(in Chiniese))

6 Royston T J，Singh R.Experimental study of a mechanical system containing a local continuous stiffness non-linearity under periodic excitation and a static load.Journal of Sound and Vibration，1996，198(3):279～298

7 Ozer M B，Ozguven H N，Royston T J.Identification of structural non-linearities using describing functions and the Sherman-Morrison method.Mechanical Systems and Signal Processing，2009，23(1):30～44

8 Ferreira J V.Dynamic response analysis of structures with nonlinear components［PhD Thesis］.London:Imperial College，1998

9 Siller H R.E.Non-linear modal analysis methods for engineering structures［PhD Thesis］.London:Imperial College/University of London，2004

10 Arslan O，Aykan M，Ozguven H N.Parametric identification of structural nonlinearities from measured frequency response data.Mechanical Systems and Signal Processing，2011，25(4):1112～1125

11 Nayfeh A H，Mook D T.Nonlinear oscillations.New York:John Wiley，1979