焦作市龙寺废弃矿山边坡危岩体稳定性及其稳定可靠度研究

李雄峰，陈鹏宇，师华鹏

（1.中国地质大学工程学院，武汉 430074；2.内江师范学院，内江 641100）

1 引言

改革开放以来，我国经济步入了快速发展的轨道，矿山开采数量及规模都得到了突飞猛进的发展。截止目前，我国共有中大型矿山9 000多座，小型矿山26万余座，占地面积近4×104k m2。随着矿山资源的逐步枯竭，每年有大量的废弃矿山产生，尤其对于以矿兴起的城市更是进入了“多事之秋”，遗留的大量工矿废弃土地，不仅占用了宝贵的土地资源，还对生态环境造成严重危害，给矿区人民的生产生活带来诸多不便。近年来，随着人们对环境保护的重视，矿山治理成为环保的一个重要方面。对于露天废弃矿山，由于前期开采不规范，超采、多占等因素造成矿山及周边环境恶化，同时形成大量高陡边坡及不规则采坑，产生安全隐患。矿山边坡一般坡度高、坡度大，地质结构复杂，并且在爆破开挖过程中产生大量的次生结构面。这些次生结构面与构造结构面相互交错切割形成形态各异的块体，块体失稳脱落是边坡破坏的常见形式。本文基于分块极限平衡法，对焦作市龙寺某废弃矿山边坡一危岩体开展稳定性计算，并对结构面参数敏感性进行分析，基于蒙特卡罗法提出其功能函数，对危岩体的稳定可靠度进行评价。

对危岩体稳定性评价的定性方法主要有地质历史分析法、赤平投影法、工程地质类比法等；定量计算方法主要有数值模拟法、静力计算法、人工神经网络和系统识别法等。许多学者对危岩体的稳定性评价问题进行了大量的研究。胡显明［1]等利用赤平投影法与危岩体裂隙统计进行了南门湾危岩体稳定性分区研究；王林峰［2]等基于可靠度理论建立了三种破坏模式的危岩体可靠指标和失稳概率评价模型；何满潮［3]等依据工程岩体的力学介质分类，利用块体理论与赤平投影方法，建立了块裂力学介质工程岩体中块状岩体的稳定可靠性分析模型；谢全敏［4]等将蒙特卡罗边界可靠度分析方法应用于某水利工程枢纽危岩块体的稳定性评价中，其结果与实际监测结果吻合。本文基于分块极限平衡法在蒙特卡罗法的基础上提出了矿山边坡危岩体稳定性分析的定量计算方法，在前人的研究基础上对矿山危岩块体的稳定性进行分析研究。

2 分块极限平衡法计算原理

2.1 分块方法及块间力假定

经典的块体理论假定岩体结构面为平面，结构面切割形成的块体为刚体，块体失稳模式为脱离岩体或沿结构面产生滑移等平动形式。分块极限平衡法［5－6]是根据块体滑移面的数量进行分块的，当岩体的抗剪强度指标除以安全系数时，在滑动面和分块的垂直分界面上也达到剪切极限。

具体做法是：沿滑移面的交棱线作竖直面对块体进行分割，因而一个分块只有一个滑移面，如图1所示。分块间的分界面上的作用力有：法向力→E，水平向剪切力→T及垂向剪切力→X。一般垂向剪切力较小，为使方程可解，忽略垂向剪切力→X。

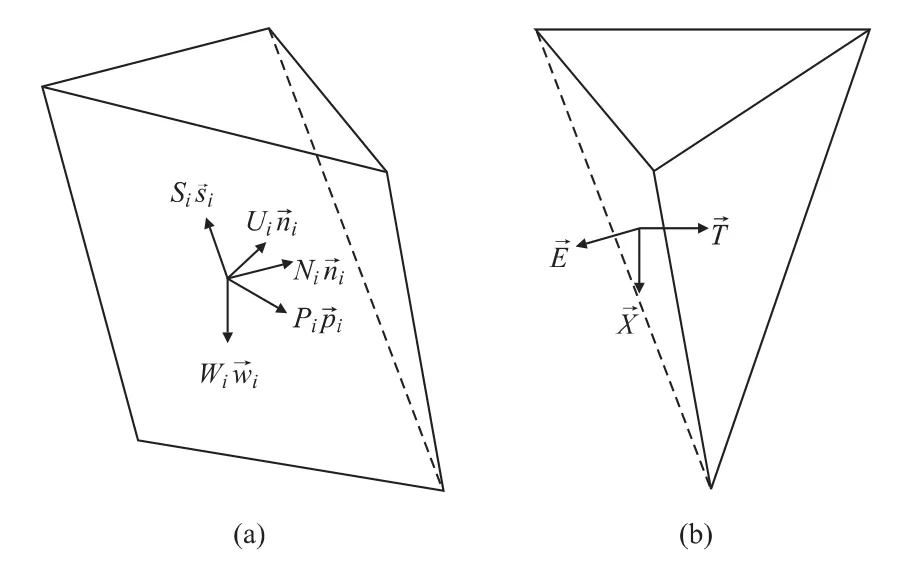
图1 分块及分块上的作用力

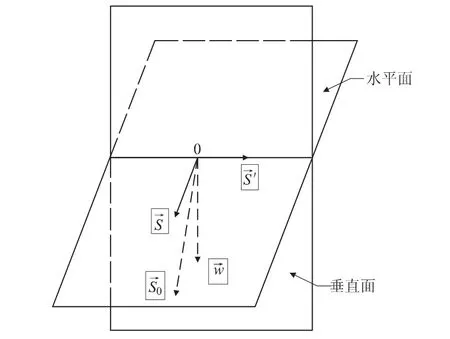
图2 三个正交方向

2.2 建立平衡方程

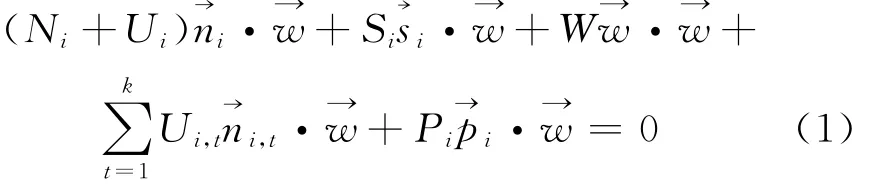
因此有：

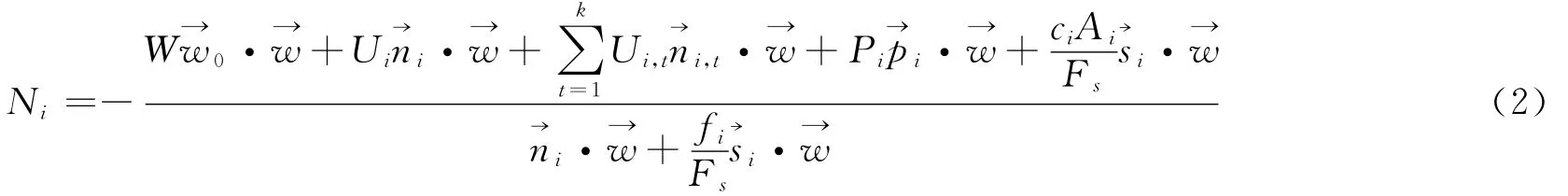
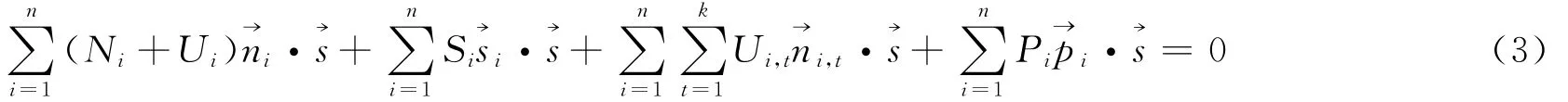
因此有：

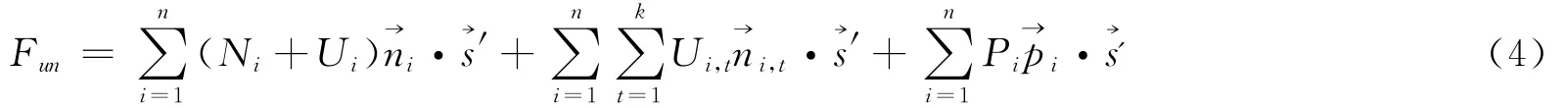
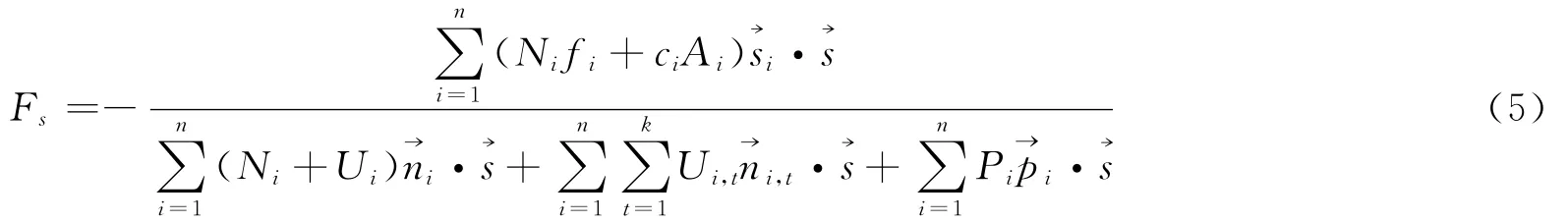
以上5式中：

Wi为分块i的重力，重力方向矢量；Ni，Ui，为分块i底滑面上的法向支持力，水压力及其方向矢量；Si为分块i底滑面上的阻滑力大小，根据强度折减定义，可表示为：

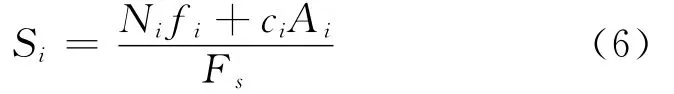
这里，ci，fi，Fs分别为滑面i的有效粘聚力，有效摩擦系数，稳定系数为分块i阻滑面上的阻滑力方向矢量。各分块的阻滑力方向矢量为过滑动方向矢量的直立面与该分块底滑面的交线方向，因此各分块的阻滑力方向矢量的水平投影方向与滑动方向相反。据此可得：

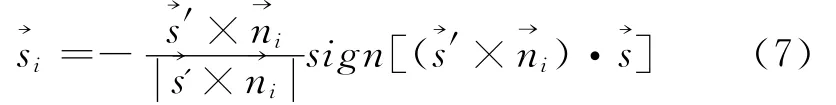
其中，Ui，t，→ni，t为分块i除滑面外其余面上的水压力，水压力方向矢量；Pi，为分块i所受的地震力、锚固力等其他外荷载的合力，合力方向矢量。

3 稳定可靠度评价［7]

3.1 基本理论

危岩块体破坏概率模型中控制危岩块体的基本随机变量为f（x1，x2，…，xm）则危岩块体破坏模式的功能函数为：

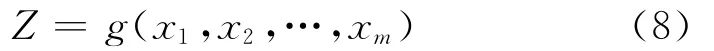
危岩块体破坏概率为：

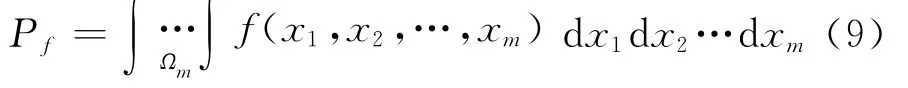
其中，Ωm表示危岩块体的破坏域；为x的概率密度函数。失效概率为：

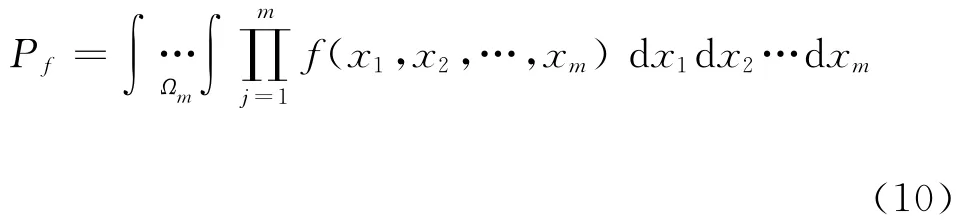
3.2 蒙特卡罗法

蒙特卡罗法［8]又称随机模拟法，是一种依据统计抽样理论，使用随机数（或更常见的伪随机数）来解决很多计算问题并利用计算机研究随机变量的数值计算方法。基于大数原理，理论上抽样次数越多，计算结果越精确，但模拟次数随置信水平和变量数呈几何级数增长。并且要产生符合某一概率分布的随机数，必须以（0，1）区间的均匀分布随机数作为基础。

危岩块体的破坏状态函数为：

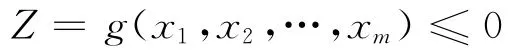
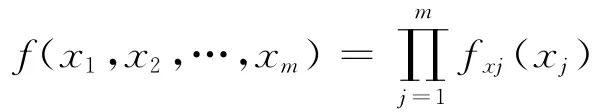
根据平均法原理，当

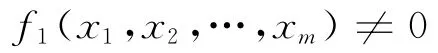
当（x1，x2，…，xm）∈Ωm且f≠0时

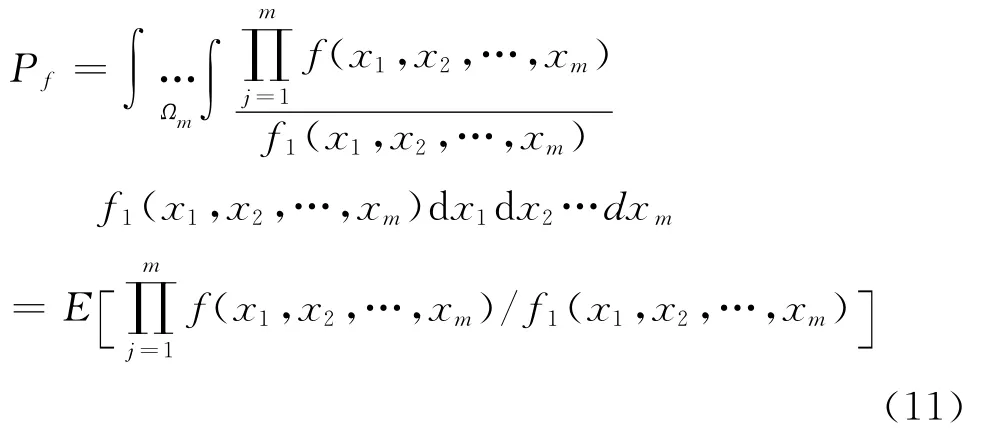
故有Z ＝g（x1，x2，…，xm）的失效概率与可靠度指标为：

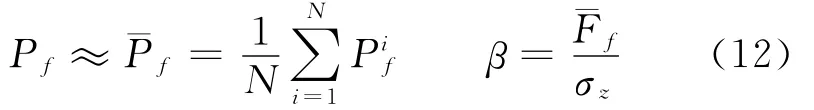
方差为：

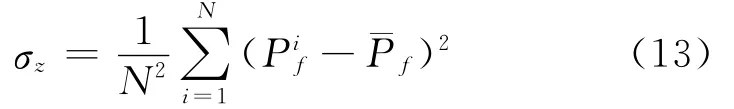
4 工程实例分析

4.1 工程地质背景

焦作市龙寺废弃矿山位于焦作市北部解放区上白作乡龙寺村，矿山所在区域属于低山丘陵地貌，边坡主要地层为奥陶系灰岩，颜色为浅灰色－灰黑色，岩层厚度为中厚层－后层状。受区域构造运动的影响，采场岩体节理裂隙发育。矿山地下水类型主要为碳酸盐岩类岩溶裂隙水，该含水岩组裂隙及溶洞发育，为接受大气降水创造了良好条件，水量丰富，雨季雨水随裂隙迳流。

危岩体的稳定性评价与稳定可靠度评价是对危岩体进行防治设计的前提。CIV－1采石场边坡位于龙寺矿山东北部，是该矿区面积最大、坡高最高的边坡，如图3所示。该边坡坡顶高程348 m，坡脚地面高程243 m，最大坡高105 m，边坡整体向西南倾斜，坡度75°～85°。由于长时间的露天开采石灰岩，爆破开挖及自然风化等因素的影响，导致区内的边坡高陡，边坡岩体节理裂隙发育，结构面整体较平直，一般有钙质填充，弱风化－强风化，裂隙面整体较平直，局部倾角变化，微粗糙。由于开挖无序以及节理裂隙发育，在边坡上部往往形成危岩体。

图3 CIV－1采石场边坡

危岩体1位于CIV－1采石场边坡中上部，该危岩体前方和左侧为临空面，右侧受岩层面切割，底部为钙质、泥质填充的软弱面，后缘发现较多陡倾裂隙和较宽的拉裂缝。危岩体1由多个危岩块体叠置构成，块体与块体之间结合差，节理裂隙张开，层面为碎块夹层，局部岩体风化破碎，上部危岩块体后缘切割面较缓。危岩体1主控结构面及节理发育情况如图4、5所示。由3组主控结构面产状与危岩体形态特征分析认为该危岩体可能破坏模式为滑塌式破坏或滑移破坏［9]。

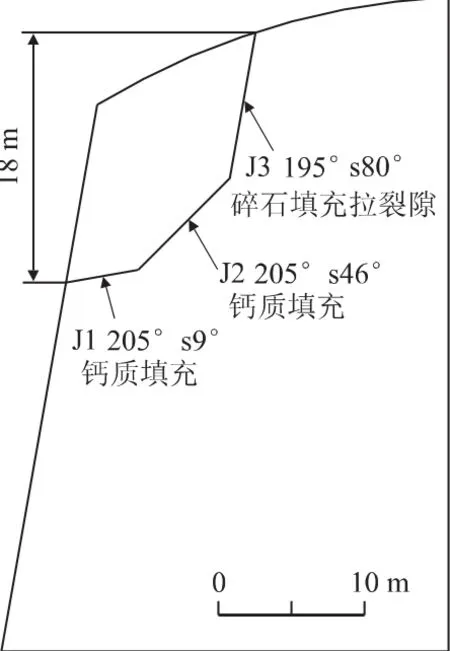
图4 危岩体1主控结构面示意图

4.2 结构面参数取值

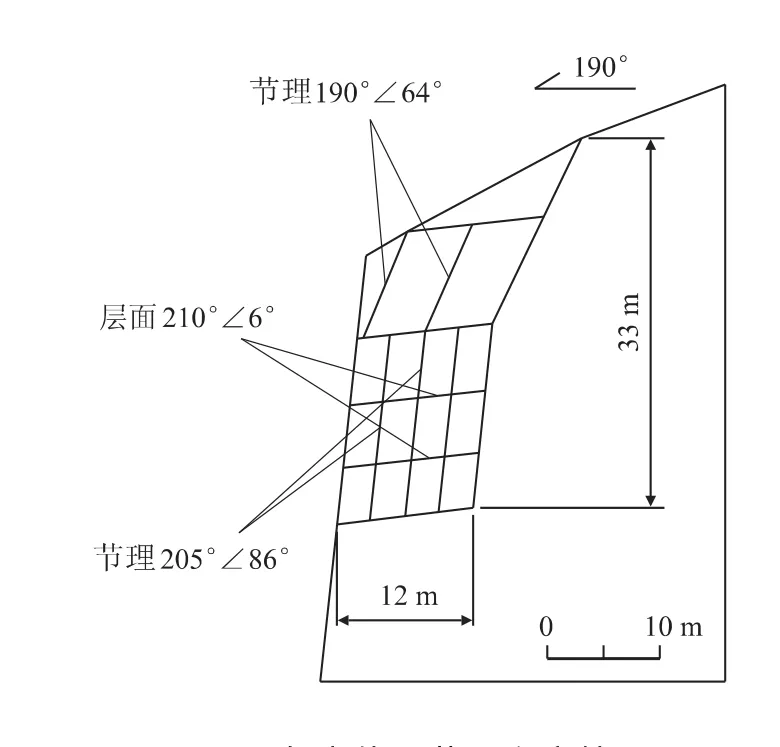
图5 危岩体1节理发育情况

根据现场调查结果显示，CIV－1采场边坡岩层产状近水平，但是节理裂隙发育，发育有两组以上有规律（产状相对固定）的结构面，边坡岩体被结构面切割成形成大小不等的块体，并且已经出现了危岩崩塌现象，由此可以认为CIV－1采场边坡属于节理控制型坡体结构，稳定性和破坏模式受控于结构面与临空面的组合特征。为得出该危岩体的优势结构面产状，根据实地勘察测量，并通过赤平投影分析［10]，危岩体1沿3个结构面（J1、J2、J3）滑动，第一组节理的走向0°～10°之间，倾向近似为东西向，在平面上与地层的走向基本垂直；第二组节理走向为290°左右，平面上与地层走向小角度相交；第三组节理走向近似为300°，与岩层走向一致。结构面等密度图和走向玫瑰花图如图6所示。

结构面的强度参数［11]常采用试验法或经验公式确定，考虑到边坡岩质坚硬，现场取样困难，对该地区的结构面进行测线法统计。本文通过现场采取摄影方式对结构面的粗造度进行数据采集，采用经验公式确定结构面的剪切强度。利用CAD得到了现场测量和拍摄的结构面表面轮廓起伏幅度，在此基础上结合锯齿状结构面几何模型，得到结构面的粗糙度系数JRC范围在3.23～7.78之间，平均值4.82。在 Barton［12]提出的JRC－JCS 模型基础上，通过摩尔－库仑准则拟合，获得剪切强度参数c、φ值如表2中所示。

4.3 分析计算

对危岩体1按照滑面数量进行分块，如图7所示。当各结构面强度参数c、φ取范围中值时，对滑动方向进行0°～360°的变化，采用分块极限平衡法计算结果如图8所示，其中法向力1、2、3分别指J1、J2、J3结构面上的法向力。当不平衡力Fun为0时，此时的安全系数Fs最小，为1.302，滑动方向为201°，不同强度参数取值对应的滑动方向及安全系数如表1所示，J1、J2、J3法向支持力分别为19 823 k N、19 830 k N、6 063 k N。

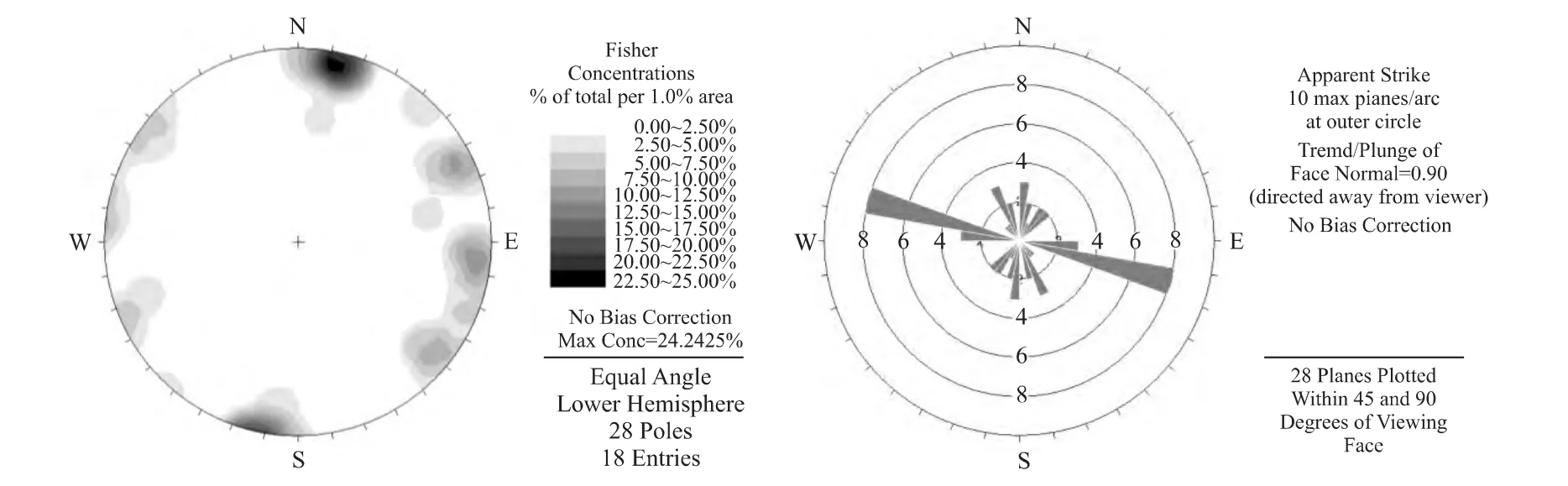
图6 结构面等密度图与走向玫瑰花图

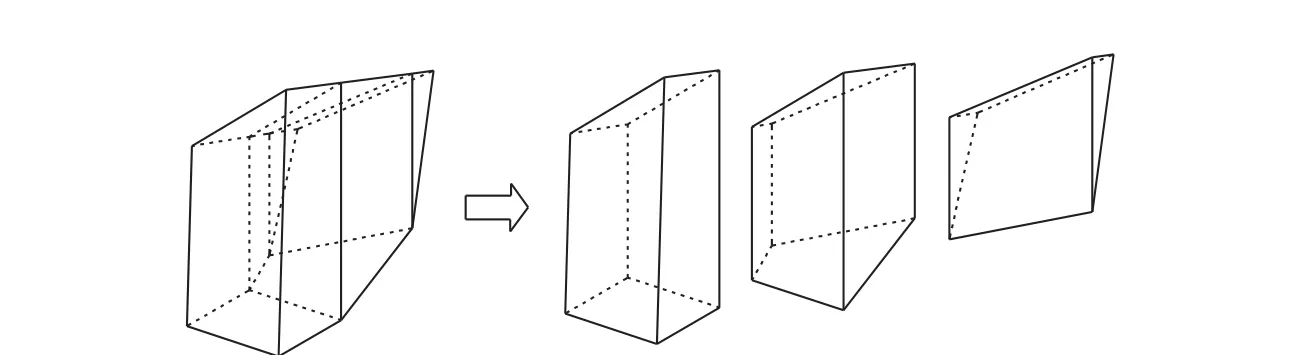
图7 危岩体1的分块

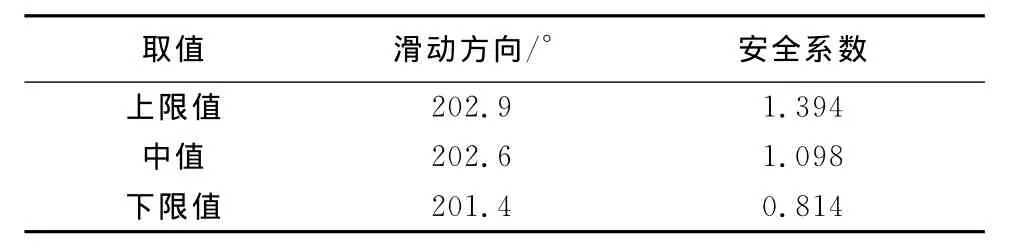
表1 不同强度参数取值对应的滑动方向及安全系数

4.4 稳定可靠度分析

该危岩体在3组主控结构面切割下易发生滑移破坏，结构面参数统计表如表2所示。根据上述评价方法提出滑移式危岩的可靠度功能函数如式（14）：

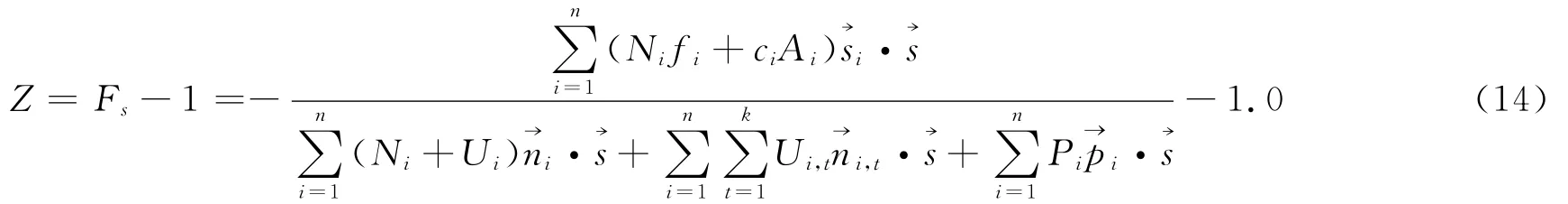
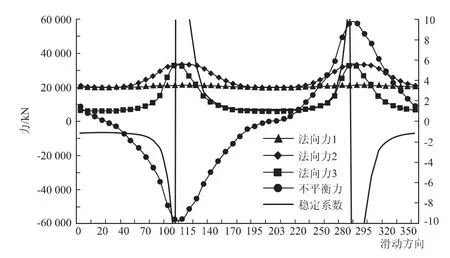
图8 分块极限平衡法稳定性系数及不平衡力随滑动方向变化图

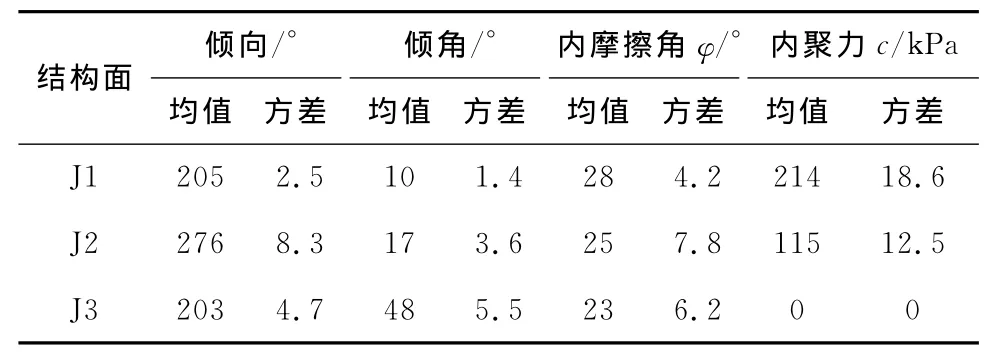
表2 结构面统计参数表

其中→s与给定的块体滑动方向即水平方位角（倾向）有关；Ni为地面上的法向支持力，即与滑动面的倾角α有关；c为结构面的粘聚力，且服从正态分布；阻滑力与tanφ有关。故综合上述关系，得到4个随即变量的均值与方差建立的危岩的可靠度功能函数可写成为：

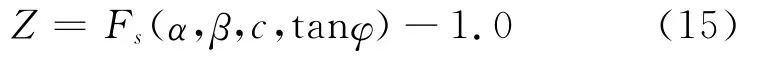
综合考虑状态函数的非线性和计算量，选取Rosenbleuth点估计法用来估计参数的概率范围。在均值点减、加一个标准差作为区间下限、上限取值点，记为下列4个取值区间：

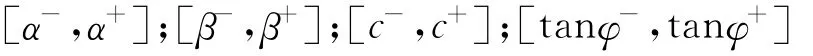
上述取值点的基本变量组合为24个，故结果中有24＝16个稳定性系数值。

由式（13）可得该16个取值的均值与方差为：

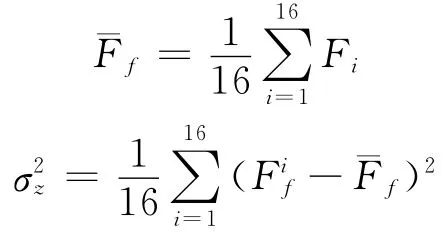
由式（11）、（12）可得可靠度指标和失稳概率为：

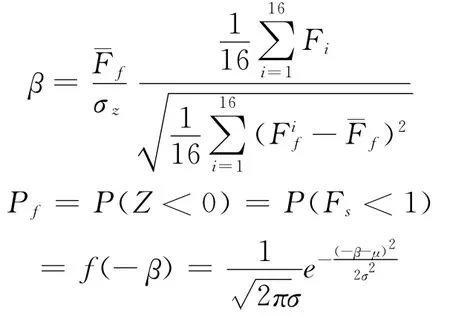
根据正态分布表获得破坏概率Pf与可靠度指标β的关系。张倬元［13]根据边坡失稳概率将边坡稳定性分为稳定（Pf＜5%），基本稳定（Pf＝5%～30%），欠稳定（Pf＝30%～60%），稳定性差（Pf＝60%～90%）和不稳定（Pf＞90%）5个等级。经计算分析得出该危岩体的可靠度指标为2.7～4.2；失稳概率为12%～27%属基本稳定区，与稳定性系数具有一致性。

5 结论

（1）本文基于分块极限平衡法，对矿山边坡稳定性进行了分析，综合考虑结构面强度参数的取值范围，得出该危岩体的安全系数在0.814～1.394之间，滑动方向为201.8°～202.7°，滑动方向为295°～305°处稳定性最差。

（2）在危岩体稳定性评价的基础上提出了稳定可靠度的功能函数，分析得到该危岩体的可靠度指标为2.7～4.2；失稳概率为12%～27%属基本稳定区，结果与实际情况相符。

（3）根据结构面剪切强度、连通与充填状态值，得到了3组主控结构面控制的危岩块体，此类受节理控制的块体中，层面与构造节理的组合方式控制着边坡的破坏模式。由于发育有两组近乎正交的陡倾优势节理，边坡中的岩体大部分都是被结构面切割形成块状或板状，且未发现楔形体结构，可能发生滑移和倾倒破坏。

（4）本方法也可应用于该地区矿山危岩崩塌灾害的评价，为应对突发性崩塌灾害防治决策提供依据。对该危岩体的治理工程，需要进一步根据相关规范公式计算各危岩体的稳定性，评价各区段的稳定可靠度，根据危岩体稳定性分区综合确定防治措施。

［1]胡显明，晏鄂川，杨建国，等.巫溪南门湾危岩体稳定性分区研究［J].工程地质学报，2011，19（3）：397－402.

［2]王林峰，陈洪凯，唐红梅.危岩稳定可靠度计算方法研究［J].人民长江，2012，43（23）：14－17.

［3]何满潮，苏永华，景海河.块状岩体的稳定可靠性分析模型及其应用［J].岩石力学与工程学报，2012，21（3）：343－348.

［4]谢全敏，朱瑞赓，池秀文.危岩块体稳定性的可靠性分析［J].化工矿山技术1998，27（3）：1－4.

［5]李天扶，王晓岚.岩质边坡抗滑稳定分析中的潘家铮分块极限平衡法［J].西北水电，2007，（2）：4－8.

［6]张奇华.多滑面块体的分块极限平衡分析法［J].岩石力学与工程学报，2007，26（8）：1625－1632.

［7]祝玉学.边坡可靠性分析［M].北京：冶金工业出版社，1993.

［8]DUNCAN J M.Factors of safety and reliability in geotechnical engineering［J].Journal of Geotechnical and Geoenvironmental Engineering，2000，126（4）：307－316.

［9]刘宝臣，潘宗源，郑金.桂林市喀斯特危岩体发育特征及稳定性分析［J].自然灾害学报，2013，22（1）：183－189.

［10]石根华.岩体稳定分析的赤平投影方法［J].中国科学，1977，8（3）：160－171.

［11]雍睿，唐辉明，胡新丽，等.结构面抗剪强度参数线性拟合方法适用性研究［J].岩土力学，2012，33（2）18－124.

［12]Barton N.Review of a new shear strength criterion for rock joints［J].Engineering Geology，1977，（7）：287－332.

［13]张倬元，王士天，王兰生.工程地质分析原理［M].北京：地质出版社，2005.