非平稳高斯序列最大值与部分和的几乎处处中心极限定理

汪园芳， 吴群英

(桂林理工大学 理学院， 广西 桂林 541004)

非平稳高斯序列最大值与部分和的几乎处处中心极限定理

汪园芳， 吴群英

(桂林理工大学 理学院， 广西 桂林 541004)

摘要：假设{Xspan,n≥1}为标准化非平稳高斯序列，在协方差和常数列{uspan,1≤i≤n,n≥1}满足适当的条件下，获得了最大值与部分和的几乎处处中心极限定理，并优化了臧庆佩所获得的结果.

关键词：几乎处处中心极限定理； 最大值与部分和； 非平稳高斯序列； 收敛性

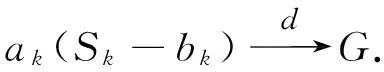
上式中：G为分布函数.

对于G的任意连续点x都有

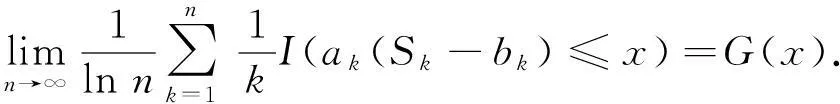
上式中：I(·)为示性函数.

Fahrner等[3]及Cheng等[4]将部分和形式的几乎处处中心极限定理推广到最大值形式的几乎处处中心极限定理.Csaki等[5]将几乎处处中心极限定理应用到平稳高斯列.Dudzinski[6]将部分和形式的几乎处处中心极限定理推广到部分和与最大值的形式，记

对任意x,y∈R,有

上式中：I(·)为示性函数；Φ(·)为标准正态分布函数.

Zang[7]将部分和与最大值的几乎处处中心极限定理从平稳的高斯序列推广到非平稳的高斯序列,本文在Zang[7]的基础上将权重从1/k推广到exp(lnβk)/k.记X1,X2,…,Xn为标准化的非平稳高斯序列，有

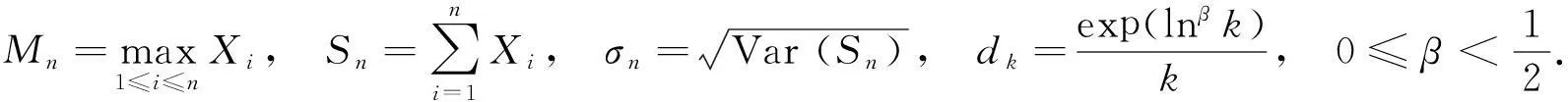
记an～bn表示当n→∞时，an/bn→1，an≤bn表示当n→∞时，存在常数K>0使an≤Kbn.

1主要结果

定理1假定{Xn,n≥1}为标准化非平稳高斯序列，其协方差阵中的元素ri,j满足

且对任意n≥1，有

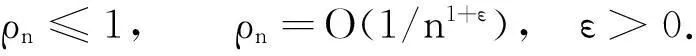
如果常数列{un,i}满足n→∞，对某τ≥0,有

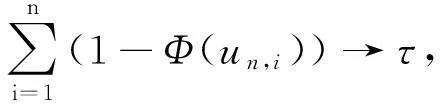
则对任意x∈R,有

(1)

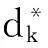
2几个引理

引理1[8]设ξ1,ξ2,…为一列有界的随机变量序列，如果存在ε>0使得

成立, 则有

引理2[9]设{Xn,n≥1}为标准正态变量，ri,j=Cov(Xi,Xj)，则对任意的实数ui,i=1,2,…,n,有

引理3[7]在定理1的条件下，对1≤k0有

证明由文献[7]得到

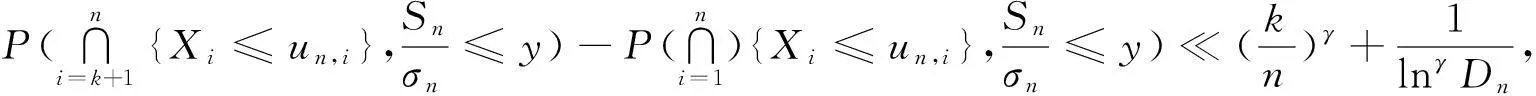
由文献[8]可知

(2)

由式(2)，引理得证.

引理4[10](Toeplitz引理) 设实数{xn;n≥1}满足

如果x=0，并且实数阵列{an,k;n≥1,k≥1}符合条件

则有

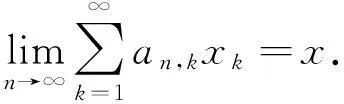
3定理1的证明

证明当β=0时，文献[7]已经给出证明，因此，只需证明0<β<1/2这种情况下成立即可.

当0≤ri,j≤ρ|i-j|时，有

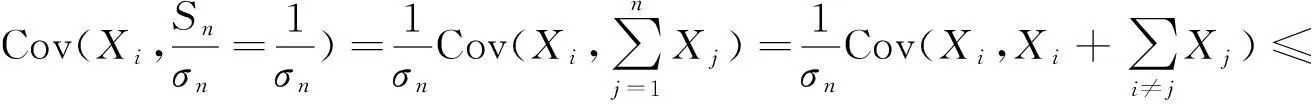
(3)

因此，存在δ和n0，对任意n>n0，有

(4)

设Yn是一标准化随机变量，且与Sn/σn有有相同的分布，并且与(X1,X2,…,Xn)相互独立，则由正态比较引理和式(4)得

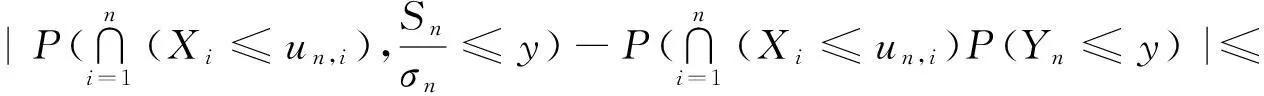
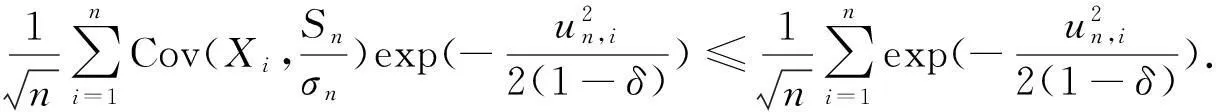
定义vn,使1-Φ(vn)=1/n，由文献[9]知

(5)

再由式(5)可得

(6)

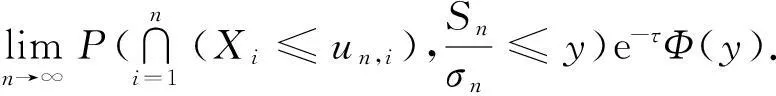
再根据引理4,得到

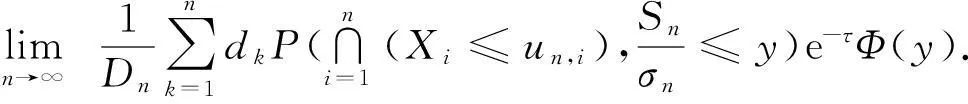
(7)

所以要证明定理1，只要转换成证明

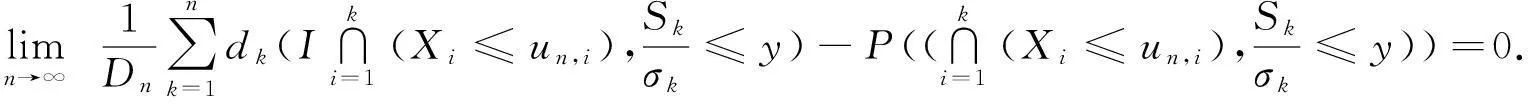
(8)

根据引理1，要证明式(8)，只要证明存在某ε>0，对任意y∈R，使

(9)

(10)

(11)

下面再来估计T2，首先来估计|E(ξkξl)|.由引理3推出

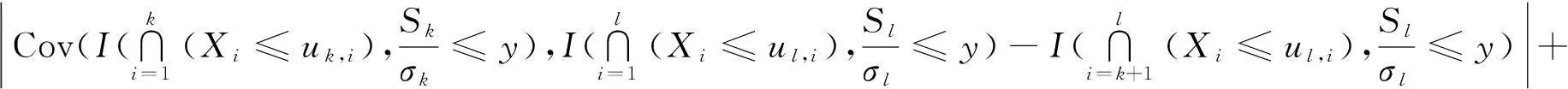
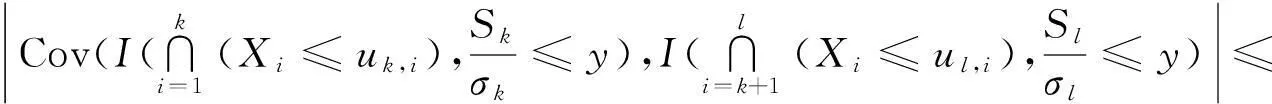
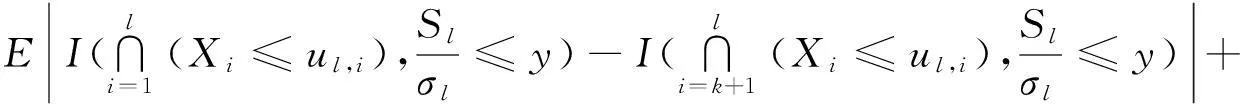
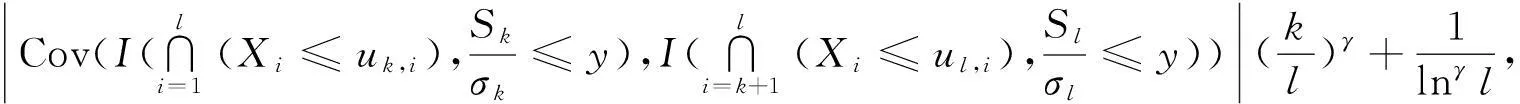
(12)

由定理1的条件知

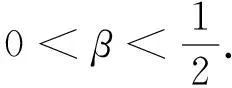
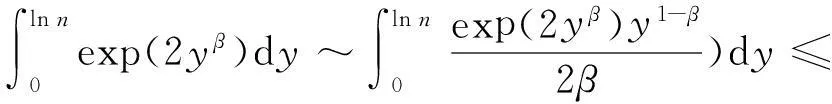
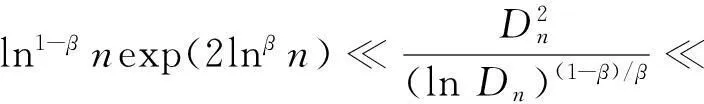
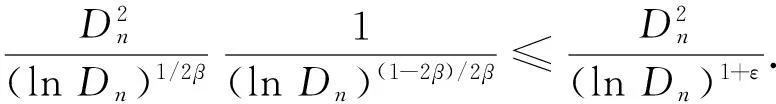
(14)

取0<ε<γ/β-2，再根据式(2)推出

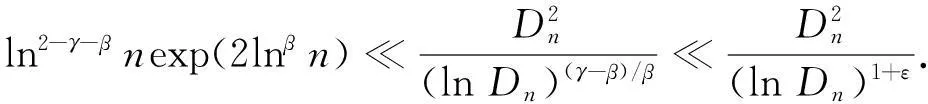
(15)

结合式(10)~式(15)，则式(9)成立.由引理1，则式(8)成立.再根据式(7)，定理1得证.

参考文献：

[1]BROSAMLERGA.Analmosteverywherecentrallimittheorem[J].MathProcCambPhilosSoc，1988,104(3):561-574.

[2]SCHATTEP.Onstrongversionsofthecentrallimittheorem[J].MathNachr，1988,137(1):249-256.

[3]FAHRNERI,STADTMULLERU.Onalmostsurecentralmax-limittheorems[J].StatistProbabLett,1998,37(3):229-236.

[4]CHENGShi-hong,PENGLiang,QIYong-cheng.Almostsureconvergenceinextremevaluetheory[J].MathNachr,1998，190(1):43-50.

[5]CSAKIE,GONCHIGDANZANK.AlmostsurelimittheoremsforthemaximumofstationaryGaussianSequences[J].StatistProbabLett,2002,58(2):195-203.

[6]DUDZINSKIM.ThealmostsurecentrallimittheoremsinthejointversionforthemaximaandsumsofcertainstationaryGaussiansequences[J].StatistProbabLett,2008,78(4):347-357.

[7]ZANGQing-pei.Almostsurecentrallimittheoremforanon-stationarysequence[J].JInequAppl,2010,10:1155-1163.

[8]WUQun-yin.Almostsurecentrallimittheoryforproductsofsumsofpartialsums[J].ApplMathJChineseUniv,2012,27(2):169-180.

[9]LEADBETTERMR,LINDGRENG,ROOTZENH.Extremesandrelatedpropertiesofrandomsequencesandprocesses[M].NewYork:Springer,1983:84-85.

[10]吴群英.混合序列的概率极限理论[M].北京：科学出版社，2006:89-90.

(责任编辑： 陈志贤 英文审校： 黄心中)

Almost Sure Central Limit Theorem for Maxima and Partial

Sums of Non-Stationary Gaussian Sequence

WANG Yuan-fang, WU Qun-ying

(College of Science, Guilin University of Technology, Guilin 541004, China)

Abstract：Suppose {Xspan,n≥1} is a standardized non-stationary Gaussian sequence. The almost sure central limit theorem for maxima and partial sums is derived under some conditions on the covariance function and the constant sequence {uspan,1≤i≤n,n≥1}. The result generalizes the one obtained by Zang Qing-pei.

Keywords：almost sure central limit theorem; maxima and partial sums; non-stationary Gaussian sequence； convergence

基金项目：国家自然科学基金资助项目(11361019)； 广西省研究生教育创新计划资助项目(YCSZ2014158)

通信作者：吴群英(1961-)，女，教授，博士，主要从事极限理论的研究.E-mail:wqy666@glut.edu.cn.

收稿日期：2014-05-21

中图分类号：O 22.4

文献标志码：A

doi:10.11830/ISSN.1000-5013.2015.01.0116

文章编号：1000-5013(2015)01-0116-05