二维直方图的HEVC帧内快速深度决策算法

许东旭, 林其伟

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

二维直方图的HEVC帧内快速深度决策算法

许东旭, 林其伟

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

摘要：针对高效率视频编码(HEVC)帧内预测高额的计算复杂度，提出一种基于二维直方图的快速深度决策算法.首先，对当前最大编码单元(LCU)采用3×3矩阵进行滤波；然后，分别统计原始LCU以及滤波后LCU的像素分布，生成二维灰度直方图.通过该二维直方图所表征的纹理特征，进行深度的自适应选择，减少不必要的深度计算.实验结果表明：同原始HM10.1相比，文中提出的算法可以节省编码时间21.6%，同时保证视频质量几乎不变.

关键词：高效率视频编码； 深度； 二维直方图； 快速模式选择； 编码单元； 灰度直方图

高效率视频编码(high efficiency video coding,HEVC)是继H.264之后，又一新的视频编码标准.相比H.264,它引进了大量的创新技术，即更多编码单元尺寸的选择及更多帧内预测模式的选择.同时，创新性地引入了3种新型编码单元的概念：编码单元(coding unit，CU)，预测单元(prediction unit，PU)，变换单元(transform unit，TU).这些创新技术使HEVC相比于H.264在提供相同视频质量的同时，又可节省将近50%比特率[1]，但是它也引入了巨大的计算复杂度.如为了得到最优的CU，HEVC需穷尽地递归搜索CU,PU,TU的最优组合[2]，同时对于每个CU帧内又需要遍历高达35种的预测模式.所以，现阶段很多学者围绕CU尺寸的快速选择以及帧内模式的快速决策这2个角度，做了大量的努力.Silva等[3]利用5个滤波模板求得当前PU的主要边缘方向，并依据求得的主要边缘方向进一步减少模式计算的数量.Shen等[4]对当前编码块与其周围相邻的编码块的空间相关性做了研究.Jiang等[5]利用Sobel算子提取当前CU的边缘信息，按生成的边缘梯度直方图进一步排除冗余的预测模式.Ting等[6]利用DCT变换后的系数进行边缘检测，以此进一步减少模式数量.Xu等[7]的前期工作对基于自相关函数的快速深度决策算法进行了报导.Zhang等[8]采用4个方向的梯度滤波器判断当前CU的纹理特征，提前决定当前CU是否进行分割.Kim等[9]利用离线设置的率失真代价(rate-distortion cost，RDcost)阈值，提前终止某些CU的进一步分割.文献[8-9]的主要思想都是采用某种策略终止某些块的分割进程，即对分割的子树进行修剪.上述这些算法都在一定程度上减少了HEVC的编码复杂度，但HEVC仍不利于实时应用，所以有必要进一步研究高效准确的快速算法来优化HEVC编码器.从子树修剪的角度加速HEVC的编码器是个好方法，但搜索深度仍然固定.本文从提取当前最大编码单元(largest coding unit，LCU)内部的纹理特征角度，利用改进的二维直方图法[10]，建立二维直方图与当前LCU深度之间的统计关系，提出了一种新的快速深度决策算法.

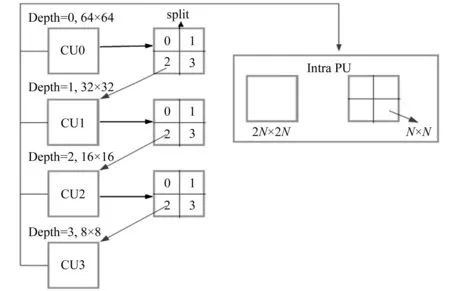
图1　递归CU结构的图解Fig.1　Illustration of the split procedure of recursive CU

1HEVC帧内预测过程

HEVC采用四叉树的递归分割结构，如图1所示.首先，当CU不划分时称为LCU，其尺寸为64×64，深度为0，对该LCU进行预测编码，得其率失真(rate-distortion，RD)代价.然后，对LCU进行分割，此时CU的尺寸为32×32，深度为1，同样对当前CU进行预测编码，得其RD代价.若当前CU尺寸为8×8时，即深度为3时，便不再进行分割.接着,从8×8的CU尺寸开始，往上进行修剪：比较4个8×8的RD代价是否小于其上一深度对应的16×16尺寸CU的RD代价，若小于，则选择8×8的CU尺寸;否则，选择16×16尺寸的CU;如此比较下去，直到深度为0.最后,选出具有最小RD代价的CU作为最终的分割模式.

对于帧内2N×2N的CU，其对应的PU尺寸只能为N×N或2N×2N.而N×N的PU在当前CU为8×8时，才被允许使用.

图2　HEVC的帧内算法流程图Fig.2　Flowchart of the intra prediction in HEVC

同时，在每个深度级上，HEVC的帧内预测需在包括2~34等33种角度预测模式以及planar和DC模式之间进行率失真优化(rate distortion optimization，RDO)计算后，选取具有最小RD代价的模式作为最优的预测模式.可见其计算量相当巨大.为了缓解对35种模式进行RDO计算所带来的高额计算复杂度，HEVC进行粗略模式选择(rough mode decision，RMD)过程[11]：首先，利用Hadamard变换代替RDO计算；然后，从35种模式中粗略选出N个具有最小的Hadamard代价(即对残差进行Hadamard变换求得该残差的变换绝对差值和，同时考虑需要编码的比特数这两者所花费的代价)作为候选模式，并且考虑了当前CU来自左边与上边CU的最有可能模式(most probable modes，MPMs)；最后，对这可能的N到N+2个候选模式进行RDO计算，从中选出代价最小的预测模式作为最优的模式.该算法极大地提高了HEVC的编码速度.帧内总的预测算法流程，如图2所示.

2基于二维灰度直方图的快速深度决策算法

文中算法之所以考虑二维直方图，是因为普通的一维直方图只是统计了某一个LCU的像素组成，不能反映出该LCU所有像素的位置信息及其内部特征.通常一个LCU块内部周围的像素相关性是非常强的，所以要充分利用这些相关性.基于上述分析，首先，根据当前像素与其周围像素的相关程度(与当前像素的距离大小)的高低采用不同的权值进行求和，并通过当前像素与滤波后的像素联立构造二维像素直方图.可见该二维直方图不仅利用了该像素本身携带的信息，而且还利用了其周围像素的信息，这在一定程度上可以反映出当前LCU的纹理特征.然后，利用该提取的纹理特征选择当前LCU最有可能的深度范围，跳过不必要的深度计算，加快编码速度.

2.1　二维直方图的构造

图像的灰度直方图是统计某一幅图像的灰度级内容，它表达了某一幅图像各个灰度级出现的次数或者概率.其横轴覆盖的灰度级范围可以表示出当前图像的色调变化情况，纵轴可以表示当前色调范围内的灰度值数量或者频率.从灰度直方图可以读出该幅图像的很多信息.比如，如果某一灰度级出现的次数很多，说明组成该幅图像的灰度值种类较少，该幅图像色调比较单一，纹理可能相对平坦；相反，如果组成该幅图像的灰度级有很多种，说明该幅图像的色调变化剧烈，纹理可能很复杂.由此可知:可以通过统计当前LCU的灰度组成，来判别当前LCU是否平坦.因为直观上，一个LCU若处于一幅图像的背景区域，那么其纹理应该相对平坦，对于纹理较为平坦的LCU，一般不可能分割到太小的尺寸；相反，一个LCU若处于图像的边缘或细节区域，那么其纹理应该会相对复杂，此类LCU一般要分割到比较小的尺寸.所以,研究一个LCU的纹理特征有助于提前决策出当前LCU需要进行RDO计算的深度级，从而跳过不必要的深度计算.

通过构造二维直方图来提取当前LCU的纹理特征.因为二维直方图不仅利用了本身的像素信息，而且也包含了周围像素的信息，这在很大程度上能够表示出当前CU的内部纹理特征.而对于纹理比较复杂的编码块，一般会分割到比较小的尺寸，即比较大的深度，对于此类编码块，可以直接跳过大尺寸分割时的编码计算；反之亦然.

为了减少计算量，首先对当前64×64 尺寸的LCU分成16×16个4×4的子块；然后，对每个4×4子块的像素进行求平均；最后，对于64×64的LCU，可以得到16×16=256个像素值.把由这256个像素所组成的LCU记为P.通常来讲，距离当前像素越近的像素与当前像素的相关程度应该越高，所以根据当前像素与其周围像素相关程度的高低分配不同的权值，同时需要满足权值的累加和为1.定义矩阵模板为

(1)

利用该模板进行滤波，并把滤波后的LCU记为Q.取P中的任一像素值(记为X)和Q中的任一像素值(记为Y)，X与Y都属于[0,255]区间内，统计由(X,Y)组成的坐标出现的次数，并把相应坐标出现的次数记为Z，可见Z属于[0,256]区间内.最后由(X，Y,Z)可以生成当前LCU的二维灰度直方图.通过以上描述可知，该二维灰度直方图不仅考虑了当前像素的信息，还包含了其周围像素的信息.

HEVC中某个典型的纹理较平坦的LCU的二维灰度直方图，如图3所示.由图3可知：通过使用HEVC的编解码参考软件HM 10.1，该LCU经过RDO计算后，最终以当前深度0作为最优的深度.HEVC中某个典型的纹理复杂的LCU的二维灰度直方图，如图4所示.由图4可知：该LCU经过RDO计算后，最终分割到了深度3.图3~4有力地证明了之前的假设，即LCU的二维灰度直方图确实能在一定程度上反映出当前LCU需要分割到的深度级.

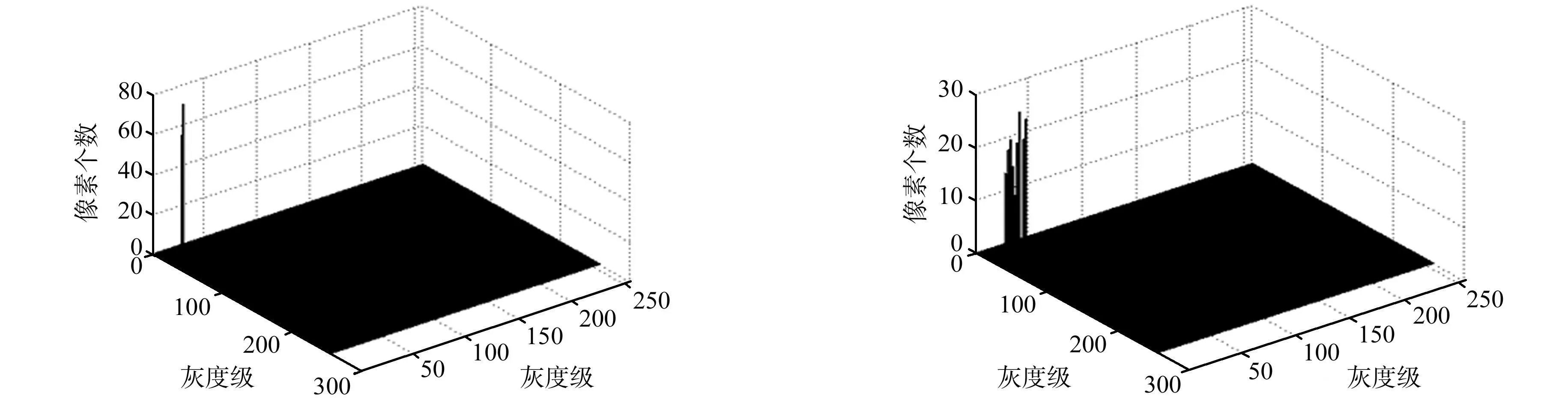
图3　典型的纹理平坦的LCU二维灰度直方图　　　　　图4　典型的纹理复杂的LCU二维灰度直方图Fig.3　Typical two-dimensional histogram 　　　　　Fig.4　Typical two-dimensional histogram of a homogeneous LCU 　　　　　　　　　of a complicated LCU

2.2　算法流程

从图3~4所示2种典型纹理的LCU的直方图特征可以进一步发现：对于图3的灰度值对应的最大像素个数是一个较大的值，说明这类平坦的LCU主要仅有几种灰度组成，很有可能是平坦的；相反，对于图4比较分散，其灰度值对应的最大像素个数值较小，说明该类LCU由多种灰度级构成，该类LCU内部的灰度变化可能会比较剧烈.根据这样的特点，考虑选取当前LCU生成的二维直方图中灰度值对应的最大像素个数值，结合设置的阈值进行判断.

经过以上分析及对大量阈值和不同序列进行测试后，基于二维直方图的快速深度决策算法具体有如下3个步骤.

步骤1对当前LCU分成16×16个4×4的子块，然后对每个4×4子块的像素进行求平均，得到256个像素值.采用式(1)所示的模板对这256个像素进行滤波，统计由该原始LCU以及滤波后的LCU的像素分布，构造二维灰度直方图.

步骤2找出该二维灰度直方图最大的像素个数值，记为max_value.

步骤3判断max_value所属的区间.如果max_value<10，则当前LCU的最小深度级设置为2；如果10≤max_value<30，则当前LCU的最小深度级设置为1；如果30≤max_value<40，则当前LCU的最小深度级设置为1，同时最大深度级设置为2；如果40≤max_value<50，则当前LCU的最大深度级设置为2；如果max_value≥50，则当前LCU的最小与最大深度级同时设置为0.

经过上述分析可知:文中算法是采用4个阈值，即10,30,40,50，将搜索的深度区间分为5种，即[2,3],[1,2,3],[1,2],[0,1,2],[0].可以看出:相比HEVC原始帧内预测算法均统一进行4个深度级[0,1,2,3]的RDO计算，采用文中算法至少可以减少1个深度级的RDO计算.若此时减少的刚好是深度级3，则可以减少64次CU的RDO计算，减少的编码时间相当可观.

为了证明4个阈值(10,30,40,50)的合理性，取纹理特征互不相同的4个序列，量化参数分别选取22，27，32，37，统计其命中率,结果如表1所示.通过表1可以看出：基于二维直方图快速深度决策算法对于测试序列命中率高达90%以上，说明文中算法可精确排除不必要的深度计算.

表1　文中算法命中率

3实验结果与分析

采用HM10.1测试模型，测试的环境为具有Intel(R) Core(TM)2 Quad CPUQ9400 @2.66 GHz,4.0 GB内存的计算机，采用VS2008编译器.因为文中只针对帧内编码进行优化，故采用的编码配置为全帧内编码模式，量化参数(quantization parameter,QP)分别选取22,27,32,37，序列全部统一编码50帧，其余为默认配置[12].

分别选取了A，B，C，D，E 5个等级的分辨率共11个序列进行测试.需要注意的是，本节所用的11个实验序列不与表1中的统计序列重合.由于文献[4]同样提出了帧内快速深度决策算法，所以本实验也实现了文献[4]的快速深度决策算法部分，用以与文中算法进行比较.采用文献[4]和文中算法与原始HM10.1比较的实验结果，如表 2所示.表2中：BDBR(Bjøntegaard delta bit rate)与Y-BDPSNR(Y-Bjøntegaard delta peak signal-to-noise ratio)是文献[13]中提出的评价准则，分别表示在同样的客观质量下，2种方法的平均码率节省情况，以及在给定的同等码率下，2种方法的平均Y-PSNR(Y-peak signal-to-noise ratio)的差异.

时间改变量Δt定义为

(2)

式(2)中:tHM10.1(QPi),tpro(QPi)分别为原始HM10.1和文中算法在不同QP值下的编码时间.

由表2可知：文中算法与原始HM10.1相比，平均Y-BDPSNR仅降低0.036 dB,平均BDBR仅增加0.865%，同时可以节省21.6%的编码时间.从表2可以进一步看出：文中算法对于像PartyScene这类纹理清晰的序列有较好的预测，基本不会影响其率失真性能，且同时可以减少23.8%的编码时间.与文献[4]相比，两者的率失真性能几乎相近，但文中算法编码时间减少量更多，提高了2.2%.文中算法是基于当前LCU块的内部纹理特征，而文献[4]是基于一帧视频内空间上的连续性，即当前LCU块与周围已编码的LCU块最优深度之间满足的较强相关性.所以，文中算法独立于文献[4]的算法，可以与其进一步融合，更大地减少HEVC的帧内编码复杂度.

表2　文中算法与文献[4]比较的实验结果

图5　文中算法与原始HM10.1算法的RD曲线Fig.5　RD curves of the proposed algorithm and original algorithm

Traffic序列(class A 2 560×1 600)分别采用文中算法与原始HM10.1算法的RD曲线，如图5所示.由图5可知：该序列采用文中算法后的RD曲线与采用原始算法的RD曲线几乎重合，即在不同的比特率上,文中算法几乎与HEVC原始算法取得相同的Y-PSNR，这也进一步说明文中算法具有较高的命中率.

4结束语

通过构造二维直方图提取当前LCU的纹理特征，并利用该纹理特征进行深度的自适应选择，跳过不必要的深度计算.实验结果表明：文中算法可以保证取得与原始HM10.1几乎相同的率失真性能，同时可以减少编码时间21.6%，极大地降低了HEVC的编码复杂度；而且，文中算法独立于现阶段出版的大部分帧内快速算法，可以与其他帧内快速算法融合,进一步减少HEVC的帧内编码复杂度.现阶段所做的研究工作都在快速CU尺寸决策的层面上进行，今后的工作将尝试对帧内35种预测模式进行优化，使多种方法融合，以更大地减少HEVC的编码复杂度.

参考文献：

[1]HAN G J,OHM J R,HAN W J,et al.Overview of the high efficiency video coding (HEVC) standard[J].IEEE Transactions on Circuits and Systems for Video Technology,2012,22(12):1649-1668.

[2]BOSSEN F,BROSS B,SUHRING K,et al. HEVC complexity and implementation analysis[J].IEEE Transactions on Circuits and Systems for Video Technology,2012,22(12):1685-1696.

[3]da SILVA T L,AGOSTINI L V,da SILVA CRUZ L A.Fast HEVC intra prediction mode decision based on EDGE direction information[C]∥20th European Signal Processing Conference.Bucharest:IEEE Press,2012:1214-1218.

[4]SHEN Li-quan,ZHANG Zhao-yang,AN Ping.Fast CU size decision and mode decision algorithm for HEVC intra coding[J].IEEE Transactions on Consumer Electronics,2013,59(1):207-213.

[5]JIANG Wei,MA Han-jie,CHEN Yao-wu.Gradient based fast mode decision algorithm for intra prediction in HEVC[C]∥2nd International Conference on Consumer Electronics, Communications and Networks.Yichang:IEEE Press,2012:1836-1840.

[6]TING Y C,CHANG T S.Fast intra prediction algorithm with transform domain edge detection for HEVC[C]∥Asia Pacific Conference on Circuits and Systems.Kaohsiung:IEEE Press,2012:144-147.

[7]XU Dong-xu,LIN Qi-wei,DONG Xiao-hui.Fast intracoding unit size decision algorithm for high-efficiency video coding[J].Journal of Electronic Imaging,2014,23(1):1-13.

[8]ZHANG Yong-fei,LI Zhe,LI Bo.Gradient-based fast decision for intra prediction in HEVC[C]∥Visual Communications and Image Processing.San Diego:IEEE Press,2012:1-6.

[9]KIM J,CHOE Y,KIM Y G.Fast coding unit size decision algorithm for intra coding in HEVC[C]∥IEEE International Conference on Consumer Electronics.Las Vegas:IEEE Press,2013:637-638.

[10]谢晶,贾克斌.一种基于二维直方图的H.264/AVC快速帧内预测判决算法[J].电子与信息学报,2005,27(7):1053-1057.

[11]ZHAO Liang,ZHANG Li,MA Si-wei,et al.Fast mode decision algorithm for intra prediction in HEVC[C]∥Visual Communications and Image Processing.Tainan:IEEE Press,2011:1-4.

[12]BOSSEN F.HM 10 common test conditions and software reference configurations[C]∥12th Joint Collaborative Team on Video Coding Meeting.Geneva:[s.n.],2013:JCTVC-L1100.

[13]BJONTEGARD G.Calculation of average PSNR differences between RD-curves[C]∥13th Video Coding Experts Group Meeting.Austin:ITU-T VCEG,2001：VCEG-M33.

(责任编辑： 黄晓楠英文审校： 吴逢铁)

Fast Depth Decision Algorithm Based on Two-Dimensional

Histogram for HEVC Intra Coding

XU Dong-xu, LIN Qi-wei

(College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China)

Abstract：In order to further reduce the great computational complexity for high efficiency video coding (HEVC) intra coding prediction high cost case, a fast depth decision algorithm based on two-dimensional histogram has been proposed in this paper. First, a 3×3 matrix is used to filter the current largest coding unit (LCU). Then, a two-dimensional histogram which is based on the distribution of gray values of the original LCU and the filtered LCU can be generated. By using the two-dimensional histogram, some of the depth levels which are unnecessary can be skipped. Experimental results show that the proposed algorithm can save 21.6% of the encoding time on average with negligible loss of coding efficiency compared with the original HM10.1.

Keywords：high efficiency video coding; depth; two-dimensional histogram; fast mode decision; coding unit; gray histogram

基金项目：福建省自然科学基金资助项目(2012J01275)

通信作者：林其伟(1959-)，男，副教授，主要从事HEVC中的快速算法的研究.E-mail:qwlin@hqu.edu.cn.

收稿日期：2013-12-23

中图分类号：TN 919.81

文献标志码：A

doi:10.11830/ISSN.1000-5013.2015.01.0023

文章编号：1000-5013(2015)01-0023-06