考虑多失效行为的核电厂可修系统可靠性数值仿真

戈道川，杨燕华，张若兴，丑 强（．上海交通大学核科学与工程学院，上海 0040；．国家核电技术公司北京软件技术中心，北京 0009）

考虑多失效行为的核电厂可修系统可靠性数值仿真

戈道川1，杨燕华1，张若兴2，丑 强2
（1．上海交通大学核科学与工程学院，上海 200240；
2．国家核电技术公司北京软件技术中心，北京 100029）

摘要：为分析含有顺序、冗余及功能相关等多失效行为的核电厂安全系统的可靠性，提出了基于动态故障树模型的可靠性数值仿真方法。通过对部件多失效行为的随机模拟及动态逻辑门成功准则的判定，实现了对含有多失效行为的核电厂安全系统的可靠性数值模拟。案例分析结果表明，该方法能对多失效行为的复杂系统进行可靠性分析，具有较强的适应性。

关键词：数值仿真；可靠性；动态故障树；多失效行为；核电厂

目前，国际上普遍采用动态故障树（DFT）模型对多失效行为系统进行可靠性建模分析。DFT在静态故障树的基础上引入了多种动态逻辑门［1］。DFT定量分析的主要方法有：状态空间法和容斥原理法。状态空间法是将DFT转化为马尔科夫链模型，通过求解Chapman－Kolmogorov微分方程［2］，来获得系统的可靠性指标。这种方法存在3个缺陷：1）要求系统满足马尔科夫性，即系统的失效和修复时间服从指数分布；2）状态空间规模随系统部件的增加呈指数型增长；3）无法对存有定期试验和维修的设备进行建模。容斥原理法［3］是通过求解不交化割序发生的概率来获取系统的不可靠度，这种方法仅适用于不可修系统。故障树的仿真分析主要集中在静态系统［4－5］，技术趋于成熟。文献［6］初步提出了一种基于最小割序集（MCSS）的DFT数值仿真技术，但未涉及如何处理部件由于维修、试验而导致的功能需求失效。此外，这种仿真技术依赖于DFT的MCSS。针对大规模、高耦合的DFT，获取完整的MCSS十分困难。

为了克服以上方法的缺陷及考虑核电厂安全系统的实际情况，本文提出一种基于模拟部件多失效行为和判定动态逻辑门成功准则的数值仿真方法。该方法无需获取系统的MCSS，直接通过模拟部件的多失效行为及判定动态逻辑门的成功准则来获取系统的可靠性指标，为含有多失效行为的核电厂安全系统可靠性评价提供一种新的分析手段。

1　可修系统可靠性指标

假设对象为连续工作的可修系统，且只有运行和停役两种状态。系统在t时刻的状态变量X（t）定义为：

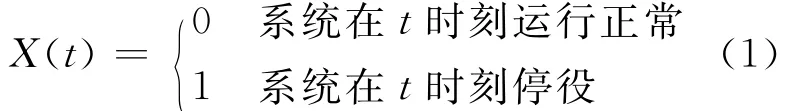
系统主要的可靠性指标（瞬时可用度、平均可用度、极限可用度）定义如下。

瞬时可用度指的是系统在某时刻能正常运行的概率［7］，用A（t）表示，则：

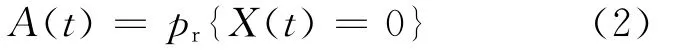
平均可用度是系统在某段时间内的平均可用性，用Aav（t）表示，则：

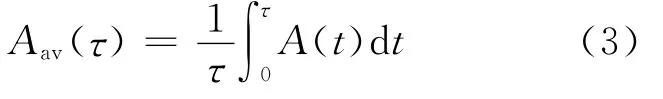
式（3）表示系统在（0，τ）时间段内的平均可用度。此外，文献［8］将系统在统计期间时间内的可用度Ac定义为：

其中：t1为工作时间；t2为统计时间

极限可用度是在统计期间无穷大时间内系统平均可用度的极限，可表示为：

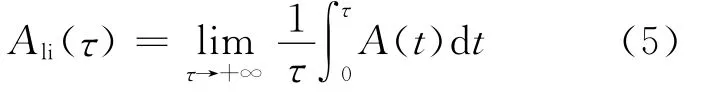
当式（5）的极限存在时，这个极限值被称为系统的极限可用度，也称为稳态可用度。

2 部件多失效行为和动态门成功准则

2．1 部件多失效行为

部件多失效行为指的是部件在发生失效时表现出的多随机性行为。系统部件按照供给功能的主次关系大致分为两类：一类为在役部件；另一类为备件（包括冷备件、热备件和温备件）。其中，冷备件在主件正常运行时处在停役状态，只有当主件失效时，才会投入运行。因此，冷备件在备用状态下不会失效。热备件则与之不同，它在备用状态下就以全功率的模式运行。因此，热备件在备用和运行工况下失效概率特性是一致的。温备件是冷备件和热备件的一个折衷方案。它在备用状态下以一个低功率的模式运行，直到替换失效的主件。通过以上分析发现，冷备件和温备件的失效行为与主件状态密切相关，本文将此类备件失效行为定义为半随机事件，定义在役部件和热备件的失效行为为随机事件。

此外，部件功能丧失的原因除随机失效外，试验、维修导致的不可用也是一个因素。这类失效是由于部件定期的试验和维修活动造成的。本文将这类活动定义为虚拟部件，并将由此引发的部件失效事件定义为确定事件。核电系统中部件多失效行为大致可归为以下3类（表1）。

表1　 部件多失效行为分类Table 1 Category of component multi－failure behavior

2．2 动态门成功准则

DFT中动态门有：优先与门（PAND）、功能相关门（FDEP）、顺序强制门（SEQ）及备门（SPARE）。此外，DFT也可能含有静态门，如与门、或门和表决门。图1为DFT中常见门。其中，椭圆形符号表示一个广义的输入事件，它既可以是一个基本事件也可以是一个门事件。圆形符号表示对象只能是基本事件。

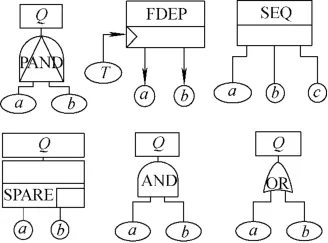
图1　 核电厂安全系统常见逻辑门Fig．1 Common logic gate for safety system of nuclear power plant

动态门成功准则是指动态门产生失效输出时，门下事件发生失效时应满足的组合和顺序条件，它可通过门的行为表达式来定义。文献［9］给出了各种门的行为表达式来定义门的成功准则，表2列出几种常见门的情况。关于更多复杂门，可参考文献［9－10］。

表2　 门成功准则的行为表达式Table 2 Behavior expression for successful rule of gate

表2中，以优先与门为例，a→b表示只有当事件a、b均失效且a先于b失效，才满足优先与门成功准则；再以两输入备门为例，（a→ba）＋（bd→a）表示a发生后b发生，则满足备门成功准则，或b先发生而后a发生同样也满足成功准则。需注意的是：当备件为热备件时，热备件在备用和运行工况下失效概率特性是一致的，故热备门的代数模型可写成（a→b）＋（b→a），这跟与门的行为表达式是一致的。因此，热备门在逻辑上等价静态与门；当备件为冷备件时，由于冷备件不可能在备用状态下失效，故冷备门的代数模型只能写成a→ba。此外，通过观察FDEP的行为表达式，发现功能相关门在逻辑上可等价地转化为静态或门。文献［10］指出顺序强制门可由冷备门的组合形式来等价表达。因此，动态逻辑门的成功准则最终可由优先与门、温备门及冷备门来表示。

3　仿真算法

3．1 部件多失效行为的仿真

假设部件具备完美的可维修性，即部件无论何时发生故障，均能立即进行维修并修复到一个全新状态。部件在时间轴上形成由交替出现的运行时间序列（T1，T2，…，Tn）和停役时间序列（O1，O2，…，On）构成的部件运行状态图，如图2所示。

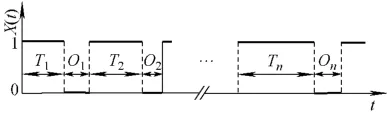
图2　 部件的运行状态图Fig．2 Running state diagram of component

假设T1，T2，…，Tn独立同分布，分布函数Fi（t）＝pr｛Ti≤t｝（1≤i≤n）；O1，O2，…，On也服从独立同分布，且分布函数Ri（t）＝pr｛Oi≤t｝。则Ti、Oi可由式（6）随机抽样获得。

式中，ε、η为在区间［0，1］上服从均匀分布的随机数，由随机数生成器产生。

针对多失效行为是随机事件的部件，其运行状态总是运行和停役交替出现（图2），可由式（6）直接模拟，直到达到规定任务时间。对于多失效行为是半随机事件的部件，情况稍显复杂。对冷备件来说，当主部件处在Ti时间段内，冷备件一定是停役状态。因此，冷备件的状态模拟只发生在主部件处在Oi时间段内，在此期间可由式（6）模拟得到。而对于温备件，情况更为复杂，这是因为温备件在备用和运行状态下运行功率不一，存在两个不同的失效分布函数。假设温备件在运行状态下的失效分布函数Fi（t）＝pr｛Ti≤t｝，在备用状态下的失效分布函数Gi（t）＝pr｛Ti≤t｝。显然，当主件处在停役时间段内，温备件的状态模拟则由式（6）完成。假设温备件在运行和备用状态下的修复时间分布是一致的，则当主件处在运行时间段内，温备件的运行状态可由式（7）模拟。

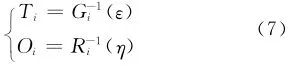
此外，鉴于虚拟部件的发生已事先确定，这类活动的影响应在部件的状态图上首先得到确认。因此，部件多失效行为的模拟仿真可按照确定事件→随机事件→半随机事件的顺序进行。

3．2 门成功准则的判定

在完成对部件多失效行为的数值仿真后，需对门成功准则进行判定以确定系统发生故障的时间序列。通过比较门下所有输入事件（包括门事件和基本事件）的运行状态图，最终确定目标系统的失效时间段。首先以两输入优先与门系统为例，成功准则判定示意图如图3所示。

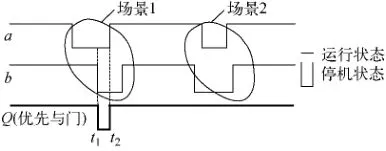
图3　 优先与门成功准则判定示意图Fig．3 Judging diagram for successful rule of PAND

在图3的场景1中，部件a和b均失效，且a先于b失效。根据优先与门成功准则，场景1显然符合。两部件失效区间的交集［t1，t2］即为系统的停役时间。而场景2中，尽管两部件均失效，但部件a后于b失效，故系统不会失效。

再以两输入冷备门系统为例，其成功准则判定示意图如图4所示。

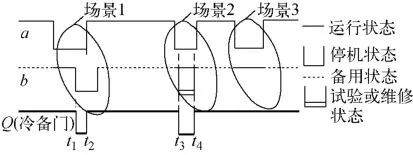
图4　 冷备门成功准则判定示意图Fig．4 Judging diagram for successful rule of cold standby door

在图4的场景1中，冷备件b在主件a的停役期间发生了随机失效，导致系统在［t1，t2］时间段内失效。场景2情况特殊，从随机抽样的角度看，冷备件b在主件a的停役期间未发生随机失效，但由于备件在此期间存在规定的维修或试验活动，导致备件b的功能需求失效，从而导致系统在备件b停役时间段［t3，t4］失效。在场景3中，冷备件在主件的失效期间未发生随机失效，系统运行正常。同理，或门、与门及温备门也可根据它们的成功准则进行判定。

3．3 统计量分析

假设系统的任务时间为Tm，通过N次仿真模拟，得到N组系统失效样本。每个样本可是一个有序的时间序列（按照时间的先后排列），也可是一个空集（说明系统在任务期间内不失效）。当样本不为空时，假设第i组样本为可得到式（8）～（12）。

系统平均可用度根据式（4）定义，则系统在N次模拟中的平均不可用度为：

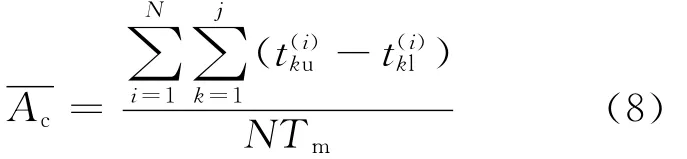
令ψi（t）为第i次模拟中系统在t时刻状态变量，则：

根据式（2），则系统在t（t≤Tm）时刻的不可用度可表示为：

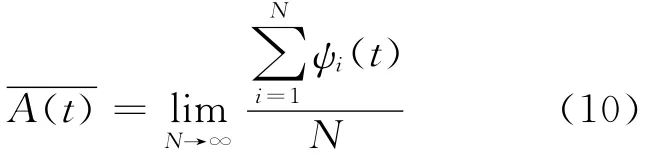
系统在t（t≤Tm）时刻的瞬时可用度A（t）可表示为

可修系统的可靠度R（t）是指系统首次故障时间超过t的概率。为了有别于式（9）的定义规则，本文定义系统在t时刻状态变量φi（t）如下：

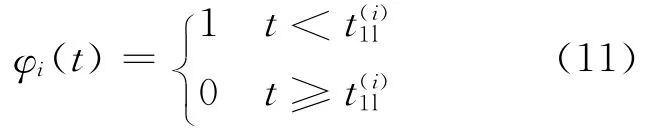
则系统在t时刻的可靠度R（t）可表示为：

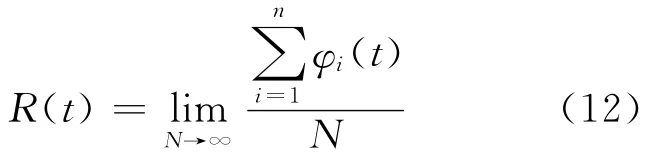
则系统在t时刻的不可靠度F（t）可表示为F（t）＝1－R（t）。

4 算例验证

算例为一个含有多失效行为的高度复杂系统，包括顺序失效、冗余失效以及功能相关失效。系统简化DFT模型如图5所示。

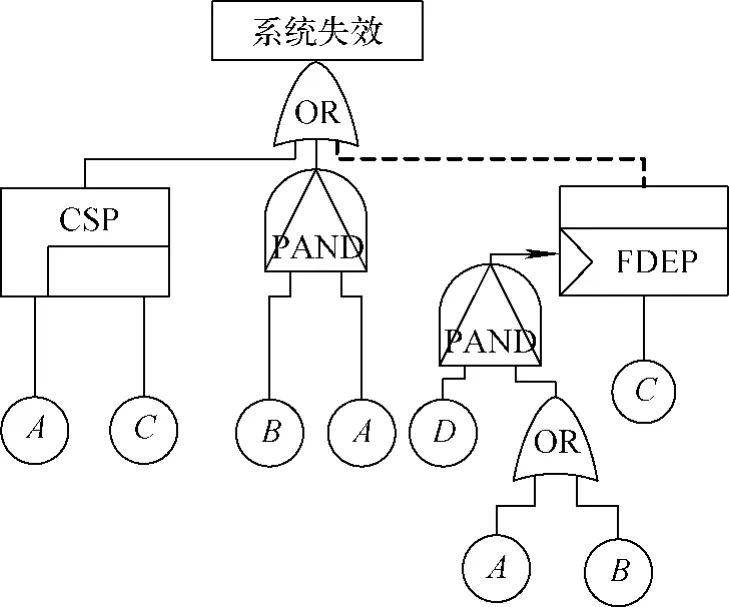
图5 算例的DFT模型Fig．5 DFT model of example

建立系统顶门成功准则的代数模型，如式（13）所示。

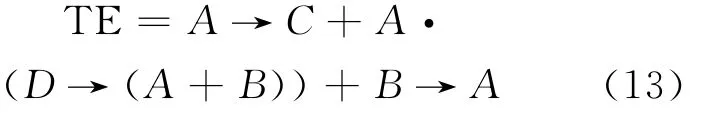
假设部件失效和修复时间服从指数分布，相关参数列于表3。

表3 部件的失效参数Table 3 Failure parameter of component

为了对比分析，采用Markov模型对算例可靠性进行精确建模分析。图6为系统的Markov模型（阴影部分表示系统处于失效状态）。

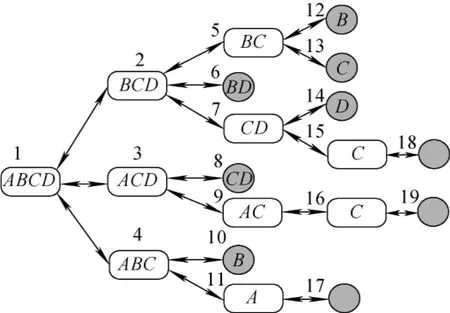
图6 算例Markov模型Fig．6 Markov model of example system

建立的系统状态概率微分方程为：

式中：P（t）＝［p1（t），p2（t），…，p19（t）］，pi（t）为系统在t时刻处在状态i的概率；Q为状态转移矩阵，可从算例的Markov模型中获取。

假设设备在初始时刻完好，则P（0）＝［1 0 00000000000000000］。P（t）可由下式求得：

则系统在t时刻的不可用度可表示为：

需注意的是，求可修系统在t时刻的不可靠度时，需将系统的失效状态定义为吸收态，即令Q中失效状态对应行的所有元素为0，这与求解系统的不可用度方法不同。

在不同时刻，分别采用Markov模型法和数值仿真法对算例进行不可靠度分析。仿真次数N＝1．0×106，计算结果列于表4。可看出，数值仿真获取的系统不可靠度与Markov模型的一致，验证了本文仿真算法的正确性。

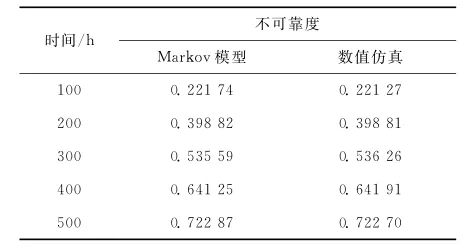
表4　 案例系统的不可靠度Table 4 Unreliability of example system

5　应用

在核电厂概率安全分析（PSA）中，全厂断电（SBO）事故的严重程度仅次于冷却剂丧失事故（LOCA）和热阱丧失事故的第三重要始发事故。因此，对核电厂电力供应系统进行PSA，具有重要的现实意义。

核电厂电力供应系统主要由厂外电源和场内电源（应急柴油发电机供应）组成。正常情况下，电厂电源由电网供应，场内电源作为应急电源处于冷备用的状态。电力供应系统的故障后运行流程为：当丧失厂外电源后，通过电子传感器发送信号启动备用电源，备用电源收到启动信号后立即启动，为电厂提供电力以确保电厂的安全运行。为确保柴油发电机组的可靠性，电厂会定期对其进行试验和预防性维修。而一旦柴油发电机组处在试验或维修状态时，将丧失提供备用功能。因此，电厂的电力供应系统存在3种失效模式：1）传感器模块先于主电源失效，在丧失主电源的情况下，无法正常启动备用电源，从而导致全厂断电；2）备用电源正常启动，但在主电源修复期间发生了随机失效，导致全厂断电；3）主电源失效时，备用电源处在试验或维修状态，无法提供备用电源，导致电厂失效。根据供电系统的多失效行为，建立核电厂全厂断电事故DFT，如图7所示。

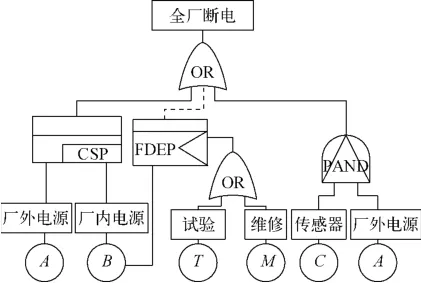
图7　 核电厂全厂断电DFT模型Fig．7 DFT model for station blackout of nuclear power plant

建立系统顶门成功准则的代数模型为：

TE＝A→B＋A·（T＋M）＋C→A（17）

假设部件的失效和修复时间均服从指数分布，系统部件的可靠性参数列于表5。

采用本文提出的方法对系统可靠性进行了数值仿真分析，通过Matlab平台编程计算，获得核电厂电力供应系统年平均不可用度为3．9×10－7（仿真次数N＝5．0×108）。这一结果表明，该电厂电力供应系统的年不可用度非常低，满足电厂可靠性设计要求。其供电系统随时间变化的平均不可用度及停役时间概率分布示于图8。

表5　 部件可靠性参数Table 5 Reliability parameter of component

图8　 系统平均不可用度及系统停役时间概率分布Fig．8 Average unavailability of system and probability distribution of system outage

6　结论

实际核电厂安全系统存在多失效行为，即顺序失效、冗余失效、功能相关失效以及试验、维修引起的设备不可用等。本文提出了一种基于部件多失效行为模拟和动态门成功准则判定的数值仿真方法。通过DFT建模和数值仿真，实现了对含有多失效行为的核电厂供电系统的可靠性分析，为系统的安全评估提供了可信数据。与以往的评价技术（如静态故障树分析法、Markov模型分析法等）相比，本文提出的数值仿真算法优势为：1）仿真模型真实反映了系统的多失效行为，是一种模拟现实技术，能对多失效行为系统进行有效的可靠性分析；2）这种仿真方法不依赖于DFT的最小割序集，通过对门成功准则的递归判定可实现对DFT的仿真计算；3）相对于传统的Markov模型法，数值仿真克服了状态空间爆炸难题，且不受部件失效和修复时间分布的限制，具有较强的适应性；4）此方法能提供更多的系统可靠性指标，如系统的平均可用度、可靠度、系统停役时间的累积分布等。

参考文献：

［1］ DUGAN J B，BAVUSO S J，BOYD M A．Dynamic fault－tree models for fault－tolerant computer systems［J］．IEEE Transactions on Reliability，1992，41（3）：363－377．

［2］ DEVOOGHT J，SMIDTS C．Probabilistic reactor dynamicsⅠ：The theory of continuous event trees［J］．Nuclear Science and Engineering，1992，111：229－240．

［3］ YUGE T，YANAGI S．Quantitative analysis of a fault tree with priority AND gates［J］．Reliability Engineering and System Safety，2008，93（11）：1 577－1 583．

［4］ 陈兆兵，曹学武．核电系统的故障树可靠性定量分析数字仿真［J］．计算机仿真，2005，22（10）：222－224．CHEN Zhaobing，CAO Xuewu．Digital simulation of reliability qualitative analysis of fault tree in nuclear power plant［J］．Computer Simulation，2005，22（10）：222－224（in Chinese）．

［5］ 文建国，孙作佩，陈争新．基于故障树的蒙特卡罗仿真在可靠性评价中的应用［J］．海军航空工程学院学报，2010，25（1）：88－92．WEN Jianguo，SUN Zuopei，CHEN Zhengxin．Research on the Monte Carlo simulation in reliability assessment based on fault tree analysis［J］．Journal of Naval Aeronautical and Astronautical University，2010，25（1）：88－92（in Chinese）．

［6］ LIANG X，HONG Y，ZHANG Y，et al．Numerical simulation to reliability analysis of fault－tolerant repairable system［J］．Journal of Shanghai Jiaotong University，2010，15（5）：526－534．

［7］ RAUSAND M，HOYLAND A．System reliability theory：Models，statistical methods，and application ［M］．Canada：Wiley－Interscience，2004．

［8］ 史进渊．发电设备主机的可靠性模型［J］．动力工程，1991，11（1）：12－16．SHI Jinyuan．Reliability model of generating equipment host［J］．Power Engineering，1991，11（1）：12－16（in Chinese）．

［9］ MERLE G，ROUSSEL J M，LESAGE J J．Algebraic determination of the structure functions of dynamic fault trees［J］．Reliability Engineering and System Safety，2001，96（2）：267－277．

［10］MERLE G．Algebraic modeling of dynamic fault trees，contribution to qualitative and quantitative analysis［D］．France：ENS de Cachan，2010．

Numerical Simulation of Reliability of Nuclear Power Plant Repairable System with Multi－failure Behavior

GE Dao－chuan1，YANG Yan－hua1，ZHANG Ruo－xing2，CHOU Qiang2
（1．School of Nuclear Science and Engineering，Shanghai Jiao Tong University，Shanghai 200240，China；2．Software Development Center，State Nuclear Power Technology Corporation，Beijing100029，China）

Abstract：To analyze the reliability of safety system having multi－failure behavior，such as sequence－，redundancy－and function－dependent failure behaviors，in nuclear power plant，a dynamic fault tree model based on numerical simulation approach was proposed in this paper．It is implemented to analyze the reliability of safety system having multifailure behavior in nuclear power reactor through randomly simulating the multi－failure behavior of component and judging the success rule of dynamic logic gate．The results of the case study indicate the proposed method is applicable for evaluating the reliability of complicated system with multi－failure behavior，and offers great generality．

Key words：numerical simulation；reliability；dynamic fault tree；multi－failure behavior；nuclear power plant

作者简介：戈道川（1984—），男，安徽六安人，博士研究生，从事核电厂概率安全研究

收稿日期：2014－04－15；修回日期：2014－07－18

doi：10．7538／yzk．2015．49．08．1410

文章编号：1000－6931（2015）08－1410－07

文献标志码：A

中图分类号：TL364．5