二维浮式结构物与完全非线性波相互作用数值分析

顾思琪，朱仁庆，吴梓鑫

(江苏科技大学船舶与海洋工程学院，江苏镇江212003)

随着海洋工程向深海发展，海洋结构物所处的海洋环境更趋恶劣.在恶劣海浪作用下，可能会产生严重的波浪爬升、相对运动和上浪等流体强非线性冲击现象，这些都会对海洋浮式结构物产生很大的局部冲击破坏载荷.因此，探索强非线性波浪与海洋浮式结构物的相互作用、发展稳定高效的数值预报方法，不仅对海洋水动力学的发展具有重要的理论意义，而且对海洋工程结构物的设计和防护具有重要的工程价值.

早期，人们对波浪与结构物完全非线性相互作用的研究大都以试验为主.近十年来，经过水动力学研究者们的不懈努力，数值方法不断获得突破，取得了令人鼓舞的成果［1］.目前，主要基于两种理论模型对其展开研究，即势流模型和粘性流体模型.基于势流理论的数值模拟中，最经典的是1976年由 Longuet-Higgins和 Cokelet［2］提出的混合欧拉-拉格朗日方法(MEL)数值模型，它可用于处理完全非线性波面运动.文献［3］中基于势流理论和高阶边界元模型，建立了无限水域中波物作用的完全非线性模型.文献［4-6］中基于完全非线性的势流理论(fully nonlinear potential theory，FNPT)，采用QALE-FEM方法模拟了方形数值水池中水波与坐底波形水坝的流固耦合响应，并将其推广成功实现了二维陡波与浮体的完全非线性流固耦合模拟.而基于粘流理论的数值水池，主要结合自由表面追踪技术，求解连续方程、N-S方程.通过引入 VOF，MAC，SPH 和 LEVEL -SET 等［7-10］重构自由面的数值方法，不但可以充分考查由于粘性作用导致的各种复杂流动特征，而且可以处理结构物在波浪激励下的大幅运动，以及波浪翻卷、破碎、合并等流体完全非线性运动等问题.因此，基于 N-S方程构建数值波浪水池，研究粘流中波浪与结构物的相互作用等问题，已成为当今国际上的一个重点发展方向.文献［11］中利用MAC差分格式，对欧拉动力学方程进行离散求解，利用VOF法处理自由表面的演变，研究了二维完全非线性波在舱内的运动特性.文献［12］中用VOF法对FPSO的上浪问题作了研究，其计算对固定的FPSO模型可以得到较好结果，但对运动的船和波浪之间的相互作用问题则尚不能给出理想结果.文献［13-14］中采用区域分解思想、远处流场和船体的运动通过势流理论来计算，船体附近的流动通过求解N-S方程来模拟，这种分开求解的方式具有一定的局限性，与真实情况中波浪与船体的相互作用有较大差别.

文中以ANSYS-14.5软件的Workbench为计算平台，结合二次开发功能，建立了具有造波和消波功能的二维数值波浪水池.文中就干舷高度不同的结构物遭遇波浪的完全非线性现象以及波浪对结构物运动响应和上浪的影响分别进行了数值模拟研究，并采用VOF法追踪自由液面，精确地描述了波浪与结构物相互作用问题，得到了结构物遭遇波浪后甲板上的上浪水位高度和结构物的纵摇、垂荡、横摇等运动响应.

1 物理模型

1.1 流体运动控制方程

控制方程包括连续方程和不可压缩粘性流体的N-S方程.

连续方程

对于不可压缩流体，方程简化为

式中:v为流体速度，ρ为流体密度.

动量方程

式中:ν为流体的运动粘性系数，Fb为作用于流体的质量力，p为流场压强.

1.2 自由液面追踪

文中采用VOF法对自由液面进行求解，由此确定自由液面的位置.自由液面的标记采用流体体积函数法，体积分数αq定义为单元内第q相流体所占体积与该单元的体积比.若αq=1则表示该单元内全部为第q相流体，若αq=0则表示该单元内没有第q相流体，若0＜αq＜1则表示该单元为交界面单元.αq满足方程

1.3 波浪理论

对于stokes三阶波，其波面方程和水质点的速度分别为［15］:

波面方程

x方向速度分量

z方向速度分量

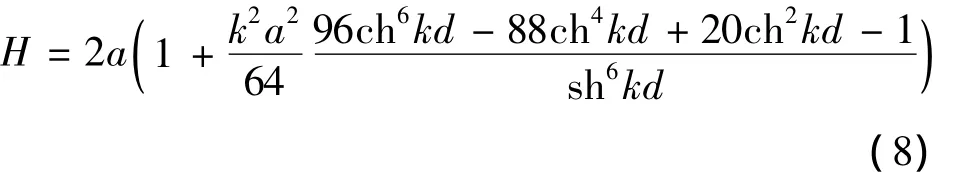
2 数值模型

2.1计算模型

文中所采用的二维数值波浪水池模型见图1.波浪水池长15m，高2 m，其中水深1.5 m，水池末端5m长的区域为消波区.坐标系原点位于入射边界的静水面处，ox轴上方全部定义为空气，密度1.225 kg/m3，ox轴下方全部定义为水，密度998.2kg/m3.

图1 数值水池示意Fig.1 Schematic diagram of the numerical wave tank

图1中将浮式结构物简化成一方形结构，长1 m，吃水0.18 m，干舷0.04 m，船体中横剖面位于x=5.5 m处.在数值计算中设置水位监测点P1、P2、P3，分别位于x=5.0 m，5.1 m和5.2 m处.

流场网格和结构网格全部采用四边形结构化网格划分.网格的质量直接影响计算结果的精度，文中经过多次试算，确定了较合理的网格划分方案:沿水池长度方向网格尺寸为dx=λ/100，沿水池高度方向网格尺寸为dz=H/8，在自由液面处对网格进行加密以提高计算精度，其高度为dz=H/30.为了适当地减少网格以减少计算工作量，在远离自由液面处网格以一定比例向上下逐渐稀疏.

2.2 边界条件及参数设置

水池顶部边界设置为压力入口条件(Pressure-inlet)，底部边界为无滑移固壁条件(Wall)，右侧边界设置为压力出口条件(Pressure-outlet)，左侧边界定义为速度入口条件(Velocity-inlet).文中基于边界造波法模拟stokes三阶波，由于软件Fluent的模块中没有提供完整的波浪模拟环境，因此需要通过用户自定义模块(UDF)，将UDF文件嵌入共享库中并与Fluent连接.

同时，在Fluent中采用非定常分离隐式求解器求解，压力方程选用加权体积力格式(Body Force Weighted)，压力速度耦合方式采用PISO算法，体积分数法为几何重构(Geo-Reconstruct)，压力参考值为一个标准大气压，重力加速度为9.8066 m/s2，时间步长为0.005s.

2.3 消波设置

为防止水池末端波浪反射而干扰入射波场，在水池末端应设置消波装置.文中采用阻尼消波方法，即在特定的消波区域内添加阻尼项以达到减弱或消除该区域内的波动.具体实现方式为在水池后端设置阻尼消波区，通过在其动量方程中添加自编UDF程序 DEFINE_SOURCE(momentum，c，t，dS，eqn)实现消波.文中采用设置速度入口造波，为了保证流动的连续性，维持质量守恒，在消波区内只需对动量方程中 z方向的分量加载 DEFINE_SOURCE((z_momentum，c，t，dS，eqn)，x方向不作处理.

消波区内，动量方程如式(9).

式中:ν为运动粘性系数;C(x)为消波系数，其函数表达式为:

式中:L为波长;x0，xL分别为消波区左、右边界的x坐标值;α为阻尼经验参数;ρ为流体密度.

3 结果与分析

3.1 波浪数值水池

稳定的波浪是波物相互作用数值模拟的前提，为了验证波浪数值水池的正确性，文中首先对波浪周期T=1.13s，理论波长λ=2 m，理论波高H=0.16 m的三阶stokes波进行了数值模拟.图2给出了数值波浪水池在x=1 m和2 m处波面(A)随时间的变化历程曲线.在波浪的传播过程中，随着传播距离的增加，波高是有衰减的，这是由于流体粘性作用的影响导致波浪能量耗散的缘故，因此，图2中x=2 m处波幅计算值与理论值偏差较x=1 m处大.总体而言，数值模拟的波形比较稳定，波浪周期、波幅参数等与理论解吻合良好，波形具有“上尖下平”的非线性特征.

图3为不同时刻波浪水池消波区内的波形图，图中较为清晰地显示了波浪的传播在受到消波区内附加阻尼的影响后波形逐渐衰减的过程.从图中可观察到，在接近水池出口处，消波区自由液面高度值已趋于0 m，从而验证了文中阻尼消波方法的可行性.

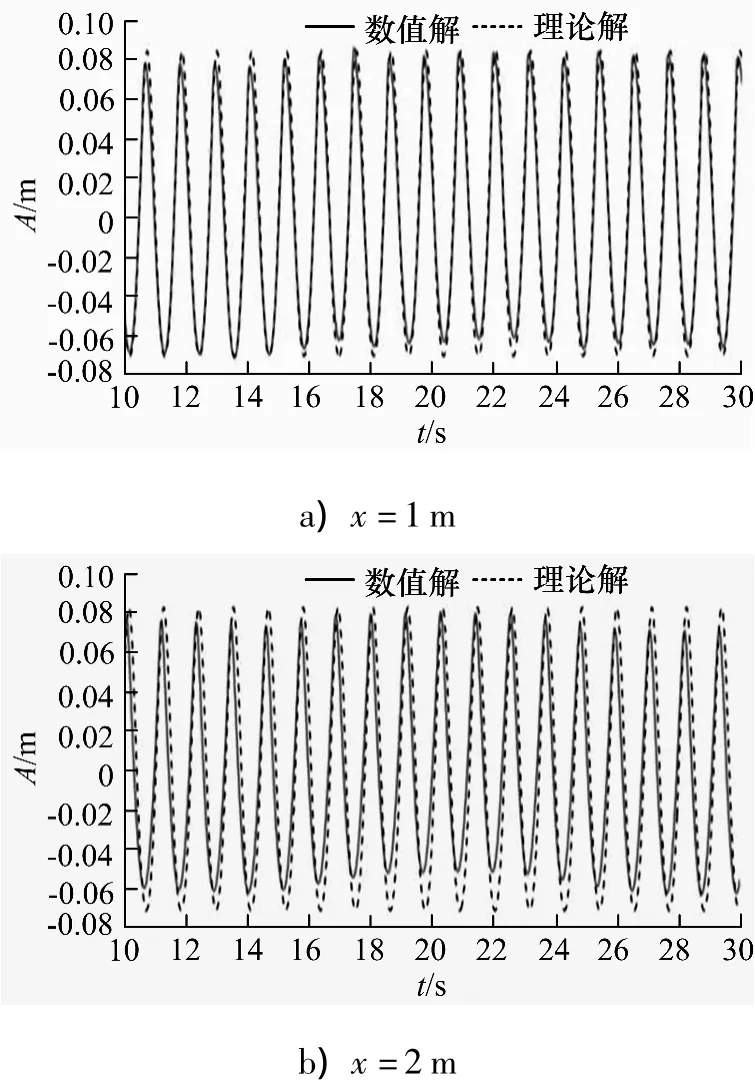
图2 数值波形与理论解对比Fig.2 Comparison of numerical and theoretical wave forms

图3 不同时刻消波区内的波形Fig.3 Waves’shape in the damping domain at different time

3.2 波浪与浮体的相互作用

3.2.1 二维甲板上浪验证实例

为验证文中计算方法的可行性和有效性，下面将基于ANSYS Workbench计算平台，对迎浪状态下二维固定结构物甲板上浪过程进行数值模拟，并将计算结果与有关文献中的试验值进行比较，以验证数值方法的有效性.波物相互作用问题是双向流固耦合问题，文中基于软件ANSYS，采用迭代耦合的方法求解流固耦合问题，其主要思路是流体方程和结构方程按顺序相互迭代求解，各自在每一步得到的结果提供给另一部分使用，直到耦合系统的解达到收敛，迭代停止［16］.

1)计算模型说明

数值波浪水池和结构模型如图4，模型尺寸与文献［16］中甲板上浪试验模型保持一致.图中水池长13.5 m，其中2 m为消波区，水深1.035 m.结构模型已简化为方形结构物，底部为半径0.08 m的圆弧，长和型深分别为1.5 m和0.248 m，吃水为0.198 m，干舷为0.05 m.

图4 计算域示意图Fig.4 Diagram of computational domain

2)计算结果

在甲板上浪的数值模拟中，波浪要素与文献［17］中试验条件保持一致，波长和波高分别为2 m和0.16 m.为了与试验结果对比，在模拟甲板上浪过程中对结构上WL1和WL2两点的波形时历进行了监测，其中点WL1位于甲板迎浪侧的首端点，点WL2与WL1的距离为0.075 m.图5为文中数值模拟结果与试验结果的对比图，由图可知，数值模拟结果与试验结果基本吻合，具体表现在结构甲板上浪时间以及甲板监测点上浪水位高度(Hs)均与试验结果基本吻合，从而验证了文中计算方法的可靠性.如图5所示，第一个波浪约在7s时到达WL1处，第二个波浪约在8s到达，且在第一个波浪涌上甲板时，部分水体被船首阻挡反射，使得船首附近的自由液面被抬高.因此，在第二个波到达船首时，波高增大许多，超过第一个波高的50%，引起的上浪现象也更为严重.

图5 FPSO模型监测点处波形时历Fig.5 Time-history of wave at probe WL1 and WL2

从数值模拟结果与试验值的对比可以看出，文中的计算方法是有效可行的，计算结果误差较小，满足计算要求，所以该方法适用于下文数值计算.

3.2.2 不同波浪要素下浮体与波浪的相互作用

具有波高、波长等波浪要素不同的规则波，对浮体的作用力也不尽相同.在与波浪接触时，结构物不仅会受到波浪的冲击载荷，而且会受到上浪水体的影响.除此之外，由于波浪的形态变化，结构物水下体积也随之发生改变，浮心位置也会发生变化，因此结构物在波浪中的运动响应是由多种因素共同作用产生的.文中针对二维问题，只考虑浮体的横摇、垂荡和横荡运动，研究浮体中横剖面模型在波浪作用下的载荷与运动响应.

图6为干舷高度为0.04 m时，浮式结构物在波高H分别为0.12，0.16 m的三阶stokes波作用下的运动响应时历曲线和上浪水位高度值.从图中可看出，在不同的波高下，结构物的垂荡与横摇曲线呈现一定的周期性，且其周期与波浪周期大致相同.第一个波浪到达甲板并发生上浪现象的时间大致为6s，在经历了第一个上浪过程后，水体的质量改变了结构物的重心，结构物的垂荡时历曲线有整体下移趋势.就上浪水位而言，对于干舷相同的结构物，波高大的波浪更容易造成上浪现象.

图6 两种波高的波浪作用下浮体的运动响应与上浪水位Fig.6 Comparison between the data of floating body with different wave heights

图7是干舷高度为0.04m时，λ分别为2m和2.5 m的三阶stokes波作用下的运动响应时历曲线和上浪水位高度(图中变量含义见上文).由于不同波长的影响，浮体的横荡值也会不同，波长较大的波浪作用下浮体的横荡值也随之增大.波长分别为2.0 m和2.5 m的波浪，其周期分别为1.13s和1.27s，在这两种波长作用下的结构物垂荡和横摇时历曲线的周期也不尽相同.观察上浪水位高度图可以发现，波长小的波浪上浪水位较大，即上浪量也随着波陡的增加而增加.这是由于在波长较大的波浪作用下结构物的横摇幅值也较大，如图7c)所示，因此在随后的上浪过程中，上浪的水体较容易随着结构物的摆动流入水池中，产生上浪水位高度较小的现象.

图7 两种波长的波浪作用下浮体的运动响应与上浪水位Fig.7 Comparison between the data of floating body with different wavelengths

3.2.3 不同干舷高度的浮体与波浪的相互作用

足够的干舷不仅可以保证船舶有一定的储备浮力，也可以减少船舶上浪.干舷高度的不同，受到波浪冲击时结构物的受力也不相同.图8为在相同波浪下，干舷分别为0.02 m和0.04 m的浮式结构物运动时历曲线和上浪水位高度图(图中变量含义见上文).与图6，7对比可发现，相对于波浪要素的影响来说，浮体干舷对结构物的横荡值影响更大些，干舷较大的结构物的漂移距离要远远大于干舷较小的结构物.而对结构物垂荡和横摇运动来说，干舷较大的结构物其运动幅值也会较大，但差值不会特别明显.在结构物发生第一个上浪过程之前，干舷高度不同的两个结构物的垂荡和横摇曲线几乎重合，在结构物发生上浪后，两者才产生了变化.原因在于，在相同的波浪下，干舷小的结构物更容易上浪，冲上甲板的水体不会立刻流回水域，而会沿着甲板流动并持续一段时间，此时这部分水体也会影响结构物的运动响应.

图8 两种干舷高度浮体的运动响应与上浪水位Fig.8 Comparison between the data of floating body with different freeboards

图9为波浪与浮体相互作用时的流体形态和结构应力云图.从图中可以观察到，上浪现象是波浪和船首下沉运动两种机制组合作用的结果.其过程是:水体沿船首升高，波浪高于船首涌到甲板上，水体沿甲板流动，从甲板另一侧流出，主要对背浪侧的流体环境产生扰动，严重时还伴有气泡和漩涡产生.在文中的计算模型中，浮体材料为结构钢，弹性模量E=2.1×1011Pa，因此结构几乎没有变形产生.但是在t=7.6s左右时，上浪部分水体流经甲板时，结构的底部与甲板的中部所受应力较大，应引起注意采取结构的加强措施.

4 结论

基于ANSYS Workbench平台的流固耦合模块，利用UDF程序进行二次开发实现速度入口造波，采用VOF方法追踪气液两项自由面，在水池后方采用动量方程中添加源项形成阻尼消波，成功建立二维数值波浪水池，实现了波浪与结构物相互作用的完全非线性数值模拟.

1)将设置造波边界法应用于Fluent模块，成功模拟了效果良好的三阶stokes波.消波区域采用阻尼消波，避免了波浪到达右端固壁边界后产生反射波.

图9 波浪与自由运动浮体的相互作用Fig.9 Interaction between wave and freely floating structures

2)采用双向流固耦合的方法，分别对不同干舷高度的结构物在不同波浪要素的波浪作用下的载荷与响应进行了对比研究，得到了结构物遭遇波浪后的运动响应和监测点的上浪水位高度，发现结构物的运动响应幅值和甲板上浪水位高度都会随着波陡的增加而增加.同时，增加结构物干舷的高度能在一定程度上减少甲板上浪，但会使其运动响应幅值尤其是横荡幅值增加，在结构设计时应加以权衡.

3)展示了波浪与浮体相互作用时的流体形态和结构应力云图，观察到了波浪与结构物相遇后波浪沿船首爬升、破碎、飞溅等完全非线性现象.并注意到上浪部分水体流经结构物甲板时，结构底部与甲板的中部所受应力较大，应注意采取结构的加强措施.

References)

［1］ Ma Qingwei.Advances in numerical simulation of nonlinear water waves［M］.Singapore:World Scientific Publishing Co Pte Ltd，2010:1 -39.

［2］ Longuet·Higgins M S，Cokelet E D.The deformation of steep surface waves on water:a numerical method of computation［J］.Proceedings of the Royal Society of London，Series A 350，1976(1660):1 -26.

［3］ Zhou B Z，Wu G X，Teng B.Fully nonlinear wave interaction with freely floating non-wall-sided structures［J］.Engineering Analysis with Boundary Elements，2015(50):117-132.

［4］ Ma Q W，Yan S.Quasi ALE finite element method for nonlinear water waves［J］.Journal of Computational Physics，2006，212:52 -72.

［5］ Yan S，Ma Q W.Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method［J］.Journal of Computational Physics，2007，221(2):666 -692.

［6］ Yan S，Ma Q W.Numerical simulation of interaction between wind and 2D freak waves［J］.European Journal of Mechanics B/Fluids，2010，29(1):18 -31.

［7］ Hirt C W，Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundaries［J］.Journal of Computational Physics，1981，39(1):201 -225.

［8 ］ Stanley Osher，James A Sethian.Fronts propagating with curvature-dependent speed:Algorithms based on Hamilton-Jacobi formulation ［J］.Journal of Computational Physics，1988(01):12 -49.

［9］ Monaghan J J.Smoothed particle hydrodynamics［J］.Reports on Progress in Physics，2005，68(8):543 -574.

［10］ Yabe T，Xiao F，Utsumi T.The constrained interpolation profile method for multiphase analysis［J］.Journal of Computational Physics，2001，69(2):556 -593.

［11］ 朱仁庆，王志东，杨松林.完全非线性波的数值模拟［J］.船舶力学，2002，6(5):14-18.Zhu Renqing，Wang Zhidong，Yang Songlin.Fully nonlinear wave simulations［J］.Journal of Ship Mechanics，2002，6(5):14 -18.(in Chinese)

［12］ Nielsen K B，Mayer S.Numerical prediction of green water incidents［J］.Ocean Engineering，2004，31(3 -4):363-399.

［13］ Kleefsman K M，Loots G E.The numerical simulation of green water loading including vessel motions and the incoming wave field［C］∥Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering.Halkidiki，Greece:OMAE，2005:981 -992.

［14］ 朱仁传，缪国平，林兆伟.运动船体甲板上浪的三维数值模拟［J］.水动力学研究与进展A辑，2008，23(1):7-14.Zhu Renchuan，Miao Guoping，Lin Zhaowei.3-D numerical simulation of green water occurrence on oscillating shuip［J］.Journal of Hydrodinamics Ser A，2008，23(1):7-14.(in Chinese)

［15］ 陶建华.水波的数值模拟［M］.天津:天津大学出版社，2005:17-252.

［16］ 朱仁庆，李辰，顾思琪，等.弹性液舱内液体晃荡研究［J］.江苏科技大学学报:自然科学版，2013，27(3):214-218.Zhu Renqing，Li Chen，Gu Siqi，et al.A study on liquid sloshing in elastic tanks［J］.Journal of Jiangsu U-niversity of Science and Technology:Natural Science E-dition，2013，27(3):214 -218.(in Chinese)

［17］ Greco M，Faltinsen O M，Landrini M.Green water loading on a deck structure［C］∥Proceedings of 16th International Workshop on Water Waves and Floating Bodies.Japan:IWWWFB，2001.