含惯容器的多层隔振系统动态性能研究

昝 浩，温华兵，范紫岩

(江苏科技大学振动噪声研究所，江苏镇江212003)

为了减少和降低舰船的辐射噪声，近年来设计的舰船中，往往将动力机械设备设计为多层隔振装置.最初在基座和基础之间通过隔振器连接所构成的单层隔振系统，其振级落差一般在20～25dB左右.对于振动噪声指标要求较高的船舶，如豪华游轮、游艇、军用舰船等，单层隔振系统已经不能满足日益增长的需求.多层隔振系统是在单层隔振系统基础上增加中间质量组成的.研究表明，双层隔振系统的振级落差一般在40～45dB左右［1］.国内外对多层隔振系统的理论和实验也进行了大量的研究［2］.为了减小船舶的振动与噪声，文献［3］中对某船用空压机组进行了浮筏隔振装置设计，其中包括隔振参数的确定以及筏体结构的设计等，探讨了提高船舶辅机浮筏隔振系统动力学性能的途径.文献［4］中利用频响函数相关系数灵敏度分析技术，对浮筏舱段结构有限元模型进行了修正.

多层隔振系统虽然能有效的提高系统的隔振性能，但是也会存在结构尺寸较大、结构复杂和安装不便等缺陷，惯容器的出现则有可能改善多层隔振系统的性能.惯容器是剑桥大学学者Smith通过研究机械网络和电路网络之间的相似性提出的［5］，将机械网络解释为一个电路，在电路中存在电阻、电感和电容3种基本元件，然而在机械网络中等同于电阻的为阻尼，电感为弹簧，将惯容器等同于电容，其主要依据是机电相似理论.2003年，Smith发明了一种惯容器机械装置，该装置具有两个端点，其中一个端点可相对于另一个端点运动，可以将它加入到机械振动系统中用来控制机械力的大小.力的大小与两个端点的相对加速度成正比，这个比例可以为常数也可以改变［6-7］.

近些年，惯容器已经有了一定的实际应用，最早应用在 F1赛车的悬架上［8］.文献［9-10］中将惯容器应用于火车悬架，改善了火车系统的动态性能及稳定性，提高了火车的舒适性和稳定性;文献［11］中将惯容器应用到车辆悬架上，提出了一种可以在全频率范围内对汽车进行减振的悬架系统.文献［12］中对惯容器进行力学性能实验，分析了惯容器的非线性对隔振效果的影响.文献［13-14］中对惯容器进行了实验测试并研究了惯容器在反馈控制中的实际问题.文献［15］中初步分析了惯容器对多层隔振系统固有频率的影响，结果表明:惯容器的使用可以降低隔振系统的固有频率.文中进一步探讨了任意一个惯容器是否会减小多层隔振系统的固有频率，分析了惯容器的位置对多层隔振系统动态性能的影响，推导了含有惯容器的多层隔振系统的传递率.

1 惯容器工作原理

1.1 滚珠丝杠惯容器机械动力学

惯容器是理想的二端元件，其中一个端点可相对于另一个端点运动，理想惯容器的动力学方程:

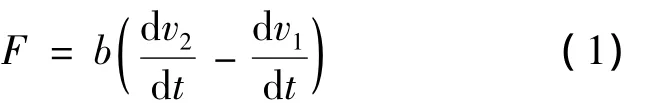
式中:F为两个端点之间的作用力;t为时间变量;v1和v2分别为两个端点的速度;b为惯容器的惯容值，单位为kg.图1为滚珠丝杠惯容器的结构示意图.激振源给丝杠施加一个等效力F，使丝杠产生线性运动并带动惯性轮作旋转运动.当螺母旋转了θ角时，丝杠行进了一个线性位移x.

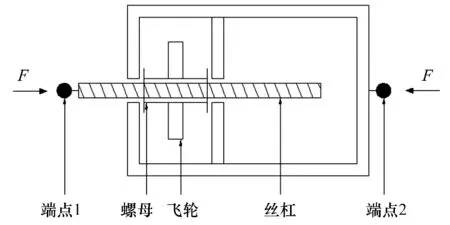
图1 滚珠丝杆惯容器原理Fig.1 Structure diagram of the ball screw inertia container

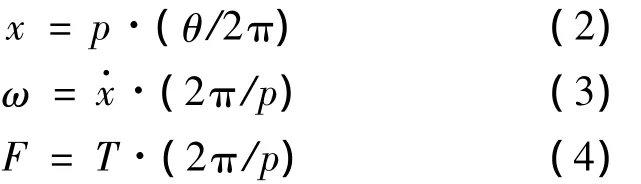
根据滚珠丝杠副的性能特点，作用在丝杠上的反力矩T与ω又有如下关系:

式中:J为惯性轮的转动惯量.

联立式(2～5)，则得到惯容器的理想惯容值b.

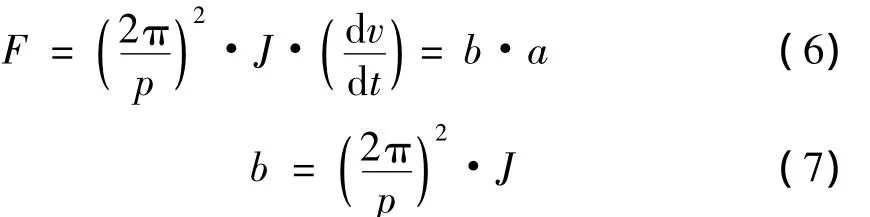
通过式(7)可以看出，滚珠丝杠惯容器的惯容值取决于滚珠丝杠副的螺距和惯性轮的转动惯量.惯容器可以把几吨重的惯性转化为几十千克飞轮的旋转惯性，并且解放了传统质量块并联接地的局限，因此具有广阔的运用前景［16］.

1.2 含惯容器速度阻抗串并联特性

根据机电类比方法，针对不同的机械结构可推导其速度机械阻抗，定性分析惯容器对隔振系统的影响.

如图2所示Ⅰ型机械系统，采用惯容器和阻尼器并联，理论上可以减缓低频振动幅值，根据3种元件的速度阻抗及阻抗特性，对应的速度机械阻抗为:

图2 机械系统结构Fig.2 Mechanical system structure

如图2所示Ⅱ型机械系统，其速度阻抗为:

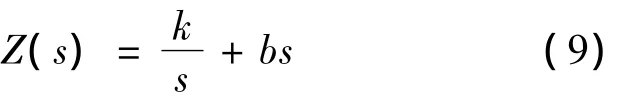
为了发挥惯容器的作用，必须在惯容器两端并联一个弹簧，即如图2所示Ⅲ型机械系统，根据3种元件的速度阻抗及阻抗特性，对应的速度机械阻抗为:

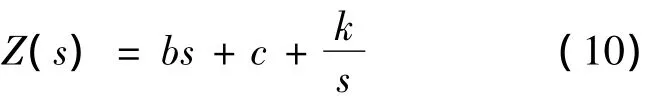
如图2所示，Ⅳ型机械系统为前3种系统串联起来的二级系统，其速度阻抗为:

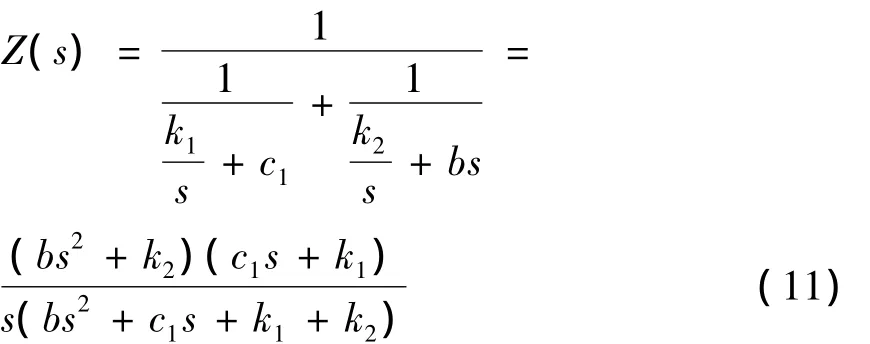
Ⅴ型机械系统为前3种系统串联起来的二级系统，其速度阻抗为:

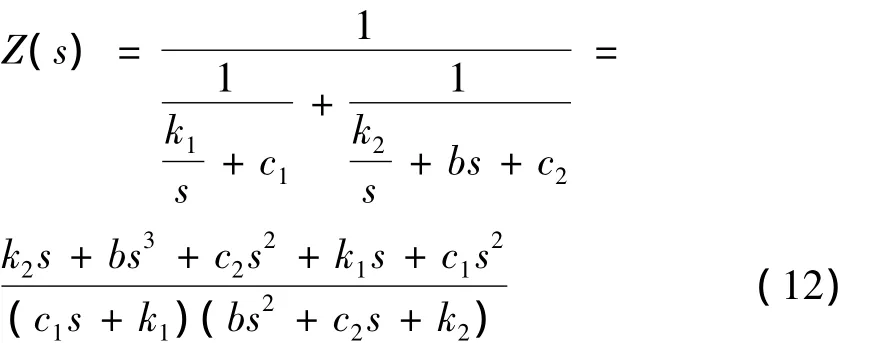
2 含惯容器多层隔振系统动态性能

ISD(Inerter:惯容器，Spring:弹簧，Damper:阻尼)隔振技术是一种通过惯容器、弹簧元件和阻尼元件组成的隔振系统，这种技术使机械网络和电子网络完全对应起来，提供了一种通过3个机械元件的组合来完善机械振动网络性能的新途径.多层ISD隔振系统如图3所示，构成多层ISD隔振系统的基本元件有3个:惯容器、弹簧和阻尼器，根据Smith所提的机电对比理论，它们分别对应电容、电感和电阻.第1层质量m1的位移为x1，所受到的扰动力为F1，第1层质量m1与第2层质量m2之间的刚度为k1，惯容值为b1，阻尼为c1;第2层质量m2的位移为x2，所受到的扰动力为F2，第2层质量m2与第3层质量m3之间的刚度为k2，惯容值为b2，阻尼为c2.以此类推，则该多层ISD隔振系统的机械动力学方程为:

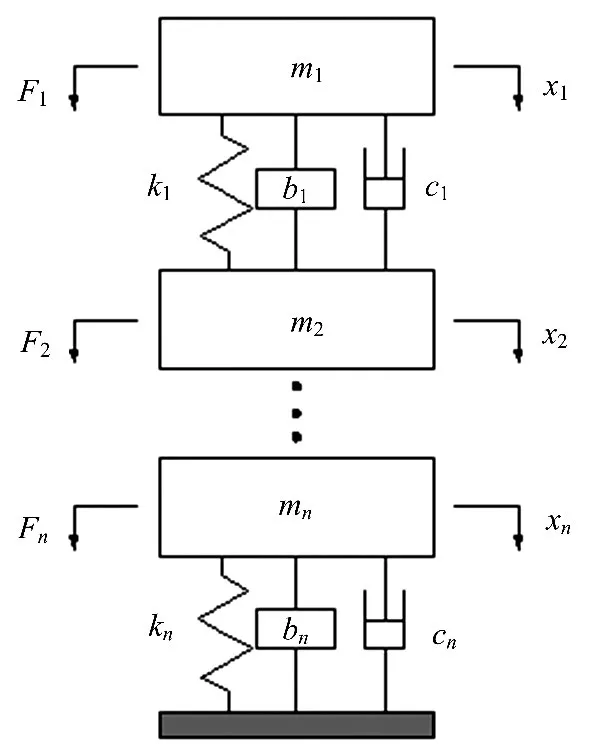
图3 含惯容器多层隔振系统Fig.3 Multi-stage vibration isolation system with inerter

对于含惯容器的多层隔振系统，其自由振动的机械动力学方程为:

则其质量矩阵M、刚度矩阵K分别为:

从式(15)矩阵可以看出，惯容值bn只是在矩阵的最后一项.这是由于惯容器bn的一端接地，另一端接中间质量mn，这相当于惯容器bn增加了中间质量mn的等效参振质量.

对于多个自由度机械系统的自由振动，其模态向量可表示为:

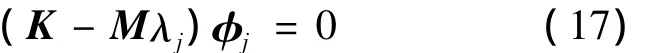
其中:j=1，2…，n;ωnj=为该系统的固有频率;φj为第j阶固有频率ωnj的模态向量，而且将φj正规化，使

若考虑第i个惯容器bi对第j阶固有频率ωj的影响，式(17)对bi求偏导，得:

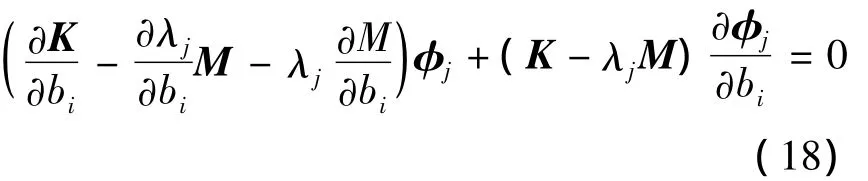
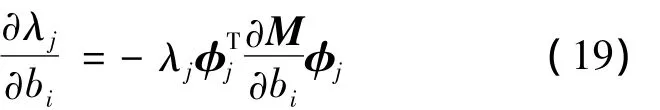
由于:

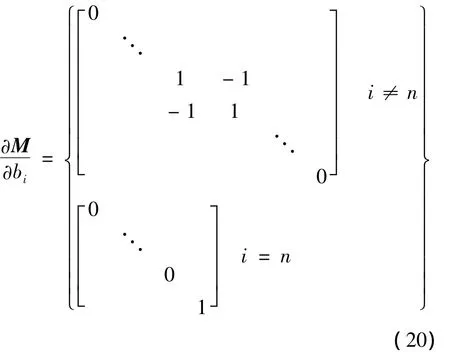
因此，可得到图3所示多自由度隔振系统中任意特征值λj对惯容值bi的偏导数:

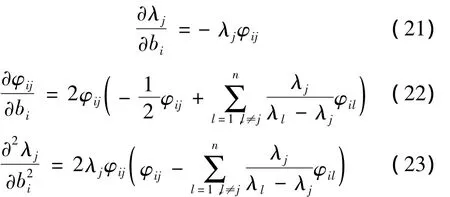
式中:

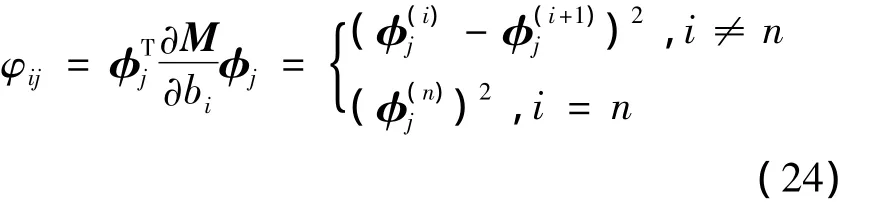
由式(21，24)得∂λj/∂bi≤0.当 i≠n时，若，∂λj/∂bi=0;或者 i=n 时，若∂λj/∂bi=0.对于一个离散的振动系统，使 ∂λj/∂bi≤0成立的充分必要条件为∂Mj/∂bi≥0.因此，对任意i，j，在多层隔振系统中任意层安装惯容器都可以减小任意阶系统的固有频率.

对于含惯容器的多层隔振系统，其机械动力学方程为:

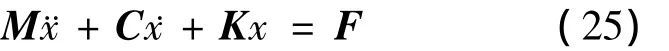
由 Zij=- ω2mij+iωcij+kij得到Z11，Z12…Znn，又由:求出Hn，式中：H1(ω)，H2(ω)…，Hn(ω)为位移频响函数，则隔振系统的传递率为:

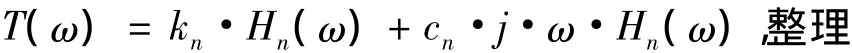
得到n层含有惯容器多层隔振系统的传递率为:

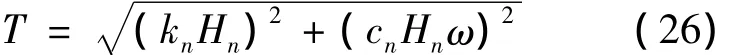
3 算例分析

以德国MTU16V396TC53柴油发电机组［17］为实例，以研究惯容器对3层隔振系统的影响.3层隔振的结构简图见图4，柴油机与发电机之间由钟状罩相连，其刚度远远大于橡胶支撑的刚度，视为无穷大，动力设备质量m1由柴油机和发电机组成;中间质量m2由组成为一体的隔声罩和支撑结构组成;筏架质量为m3.上层柴油机和发电机采用20个EIN 3164-3橡胶支撑，其垂直方向的刚度为1.335×106N/m，其中柴油机下面有12个，发电机下面有8个;中间质量和筏架之间采用10个17/1663D型橡胶支撑，其垂直方向的刚度为2.159×106N/m.筏架与基础之间采用10个17/1663D型橡胶支撑，其垂直方向的刚度为2.159×106N/m.

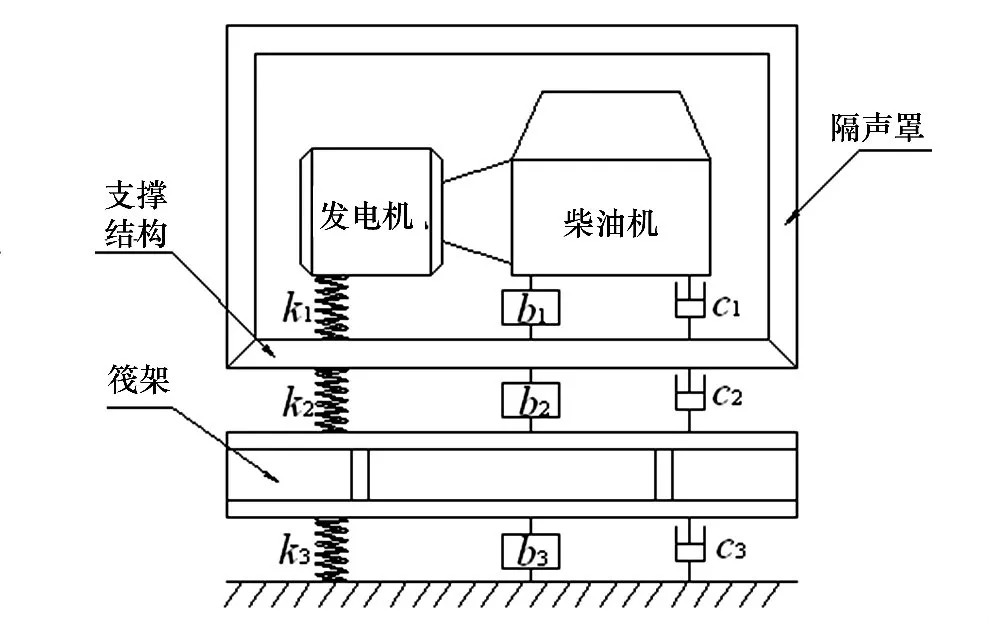
图4 3层隔振柴油发电机组Fig.4 Three-stage vibration isolation system for diesel generating sets

下文探索惯容器装在不同位置对于该3层隔振机组的固有频率及其机械导纳的影响.已知m1=11563 kg，m2=7 314 kg，m3=3 950 kg，k1=20×1.335×106=2.67×107N/m，k2=k3=10×2.159×106=2.159×107N/m.筏架和机组质量比为0.34，符合一般筏架设计规范.分别令 bi∈［0，6000］kg，另外2个惯容值为零，即:

根据|K-Mω2i|=0，可以得到图4～6计算结果.图5所示为惯容器b1对3层隔振系统固有频率ω的影响，图6为惯容器b2对3层隔振系统固有频率的影响，图7为惯容器b3对3层隔振系统固有频率的影响.结果显示，任何一个惯容值的增大都会导致系统固有频率降低.由矩阵M1，M2，M3对比可知，上层惯容器b1对质量矩阵的每一行都有影响，因此b1对系统固有频率的影响更大;而b3只是存在于质量矩阵的第3行、第3列上，因此，只是相当于增加了质量块m3的参振质量，对整个质量矩阵的影响相对较小.如图5～7所示，最上层惯容器b1可大幅度减小系统的固有频率，对第2阶、第3阶固有频率的减小幅度更大，因而缩小了第1阶和第2阶固有频率的间隔;而第2层惯容器b2在［0，6000］kg区间内有效减小了第2阶和第3阶固有频率的间隔.

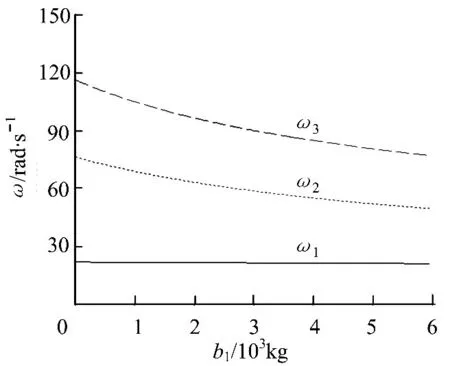
图5 惯容值b1对隔振系统固有频率的影响Fig.5 Influence of the inertance b1on natural frequency

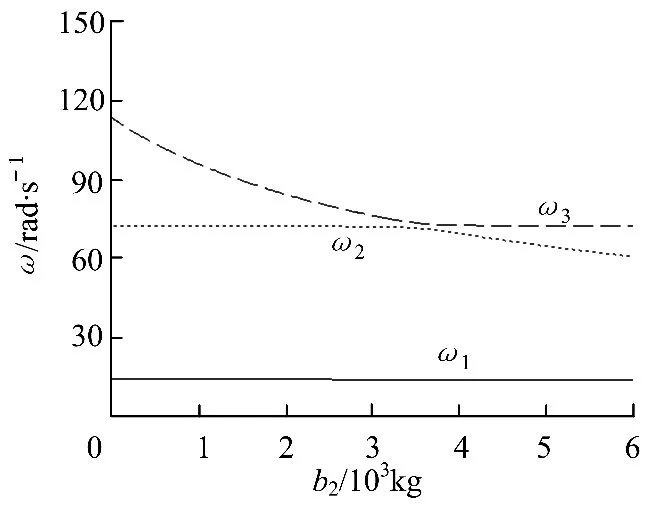
图6 惯容值b2对隔振系统固有频率的影响Fig.6 Influence of the inertance b2on natural frequency

图7 惯容值b3对隔振系统固有频率的影响Fig.7 Influence of the inertance b3on natural frequency

惯容器对3层隔振系统传递率T的影响如图8所示.由传递率I波峰的位置可知，惯容器使传递率波峰前移，即减小系统固有频率;上层惯容器使波峰前移幅度较大，即上层惯容器对第2，3阶固有频率减小幅度较大.插入上层惯容器与下层惯容器相比，第2，3个波峰比第1个波峰前移幅度大，传递率波峰间隔变小更加明显.最下层惯容器b3引起隔振系统的固有频率下降量较小，但是不会改变传递率在高频的衰减速率;其它层惯容器引起隔振系统的固有频率下降量较明显，但会导致传递率在高频的衰减速率下降，降低隔振系统的高频隔振特性.

图8 惯容器对振动传递率的影响Fig.8 Influence of the inertance on transmissibility

在算例中，令中间质量减少一半，并使惯容值为原筏架质量一半的惯容器装在下层(即b1=b2=0，b3=1975kg)，使其一端接筏架，一端基础，则改进后ISD3层隔振系统的减振效果在理论上和原双层隔振系统相同.设原双层隔振系统的质量方程为，ISD双层隔振系统的质量方程为=m/2=m/2，其中m′22，b22，所以M′=M.当惯容器的惯容值为1975kg时，惯容器的自身质量可以设计在几十千克左右，因此，ISD双层隔振系统在大大减少中间质量的情况下，仍能保持原有隔振系统的隔振效果，从而减少双层隔振系统的附加质量，有利于多层隔振系统的轻量化设计，在舰船等航行器的工程应用中具有良好的应用前景.

4 结论

1)在多层隔振系统中任意层安装惯容器都可以减小任意阶系统的固有频率，也会使各阶固有频率的间隔变小.插入上层惯容器与下层惯容器相比，上层惯容器对高阶固有频率减小的幅度较大，且使固有频率的间隔变小更加明显.

2)在实际工程应用中，在上层安装惯容器使多层隔振系统的固有频率间隔减小，从而更容易避开动力设备的扰动频率，以抑制共振峰值，但对动力设备的振动传递率产生不利影响，使其高频振动随频率变化的衰减量下降.若使惯容器的一端接地，一端接中间质量，则相当于增加了中间质量的参振质量，可以保持原有隔振系统的隔振效果，从而解决了多层隔振系统中间质量较大带来的弊端，有利于多层隔振系统的轻量化设计.

References)

［1］ 段小帅，梁青，陈绍青，等.双层隔振系统隔振效果评价与试验［J］.振动测试与诊断，2010(6):694-697.Duan Xiaoshuai，Liang Qing，Chen Shaoqing，et al.E-valuation and experiment on vibration-isolation effect of double-stage vibration-isolation system［J］.Journal of Vibration，Measurement＆ Diagnosis，2010(6):694-697.(in Chinese)

［2］ 吴广明，彭旭，沈荣瀛.多层隔振系统功率流研究［J］.噪声与振动控制，2004(3):1-4.Wu Guangming，Peng Xu，Shen Rongying.Investigation on power flow of multi-stage vibration isolation system［J］.Journal of Vibration，Measurement ＆ Diagnosis，2004(3):1-4.(in Chinese)

［3］ 方媛媛，王国治.船舶辅机的隔振设计及船体耦合振动分析［J］.江苏科技大学学报:自然科学版，2006，20(3):16-20.Fang Yuanyuan，Wang Guozhi.Design of vibration isolation for ship′s auxiliary machinery and analysis of coupling vibration with ship structure［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2006，20(3):16-20.(in Chinese)

［4］ 温华兵，王国治.基于频响函数相关系数灵敏度的浮筏舱段有限元模型修正［J］.江苏科技大学学报:自然科学版，2005，19(6):75-78.Wen Huabing，Wang Guozhi.Updating finite element model of cabin with floating raft through sensitivity analysis of FRF correlation coefficient［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2005，19(6):75-78.(in Chinese)

［5］ Hsu M S.The realizations of inerter concept and the application to building suspension［D］.Taibei:National Taiwan University，2005.

［6］ Smith M C.Synthesis of mechanical networks:The inerter［J］.Automatic Control，IEEE Transactions on，2002，47(10):1648-1662.

［7］ Papageorgiou C，Smith M C.Laboratory experimental testing of inerters［J］.Decision and Contiol Seville，2005:3351-3356.

［8］ Chen M Z Q，Papageorgiou C，Scheibe F，et al.The missing mechanical circuit element［J］.Circuits and Systems Magazine，2009，9(1):10-26.

［9］ Wang F C，Chen C W，Liao M K，et al.Performance analyses of building suspension control with inerters［C］∥Decision and Control，2007 46th IEEE Conference on.Cancun，Mexic:IEEE，2007:3786-3791.

［10］ Wang F C，Yu C H，Chang M L，et al.The performance improvements of train suspension systems with inerters［C］∥Decision and Control，2006 45th IEEE Conference on.San Diego，USA:IEEE，2006:1472-1477.

［11］ 江浩斌，耿建涛，张孝良，等.基于虚拟样机模型的车辆蓄能悬架联合仿真研究［J］.振动与冲击，2010，29(10):221-223.Jiang Haobin，Geng Jiantao，Zhang Xiaoliang.Study on co-simulation of vehicle suspension system employing inerter based on virtual protoype model［J］.Journal of Vibration and Shock，2010，29(10):221-223.(in Chinese)

［12］ 孙晓强，陈龙，汪少华，等.非线性惯容器-弹簧-阻尼悬架系统隔振性能分析［J］.农业工程学报，2013，29(23):38-45.Sun Xiaoqiang，Chen Long，Wang Shaohua，et al.A-nalysis of vibration isolation performance for nolinear inerter-spring-damper suspension［J］.Transactions of the Chinese Society of Agricultural Engineering，2013，29(23):38-45.(in Chinese)

［13］ Papageorgiou C，Analysis of experimental data from the testing of inerter devices［G］.UK:Department of Engineering， ControlGroup， UniversityofCambridge，2005.

［14］ Papageorgiou C，Houghton N E，Smith M C.Experimental testing and analysis of inerter devices［J］.Journal of Dynamic Systems，Measurement，and Control，2009(1):131.

［15］ Michael Z Q，Chen Yinlong，Hu Lixi，et al.Influence of inerter on natural frequencies of vibration systems［J］.Journal of Sound and Vibration，2014，333(7):1874-1887.

［16］ 李川，邓菊丽，王时龙，等.螺旋飞轮运动转换系统的机电比拟设计理论研究［J］.机械工程学报，2010，46(3):103-108.Li Chuan，Deng Juli，Wang Shilong，et al.Electromechanical analogy design theory of spiral flywheel motion transformation system［J］.Journal of Mechanical Engineering，2010，46(3):103-108.(in Chinese)

［17］ 沈荣瀛，卢峥.MTU柴油发电机组隔振装置振动固有特性分析［J］.振动与噪声控制，1994(3):2-7.Shen Rongying，Lu Zheng.The natural characteristic vibration analysis of MTU diesel generator set［J］.Journal of Vibration，Measurement＆ Diagnosis，1994(3):2-7.(in Chinese)