基于Rankine源法的小水线面双体科考船耐波性预报
2015-02-28谷家扬管义锋耿培腾
吴 介,谷家扬,管义锋,耿培腾
(江苏科技大学船舶与海洋工程学院,江苏镇江212003)
小水线面双体船(small waterplane area twinhull ship,SWATH)是20世纪中后期逐渐发展起来的一种船型,与普通单体船相比,小水线面使其具备良好的耐波性和较小的兴波阻力,同时小水线面双体船还有甲板面积宽阔、稳性和抗沉性好、快速性显著和操纵灵活等优点[1-3].船舶耐波性是船舶水动力学传统的研究方向之一,剧烈的摇荡运动会对船体结构、船舶安全和船舶设备工作等产生影响[4].良好的耐波性使得小水线面双体船在某些方面比单体船具有更多优势,如科学考察时能保证仪器、设备工作的稳定性和测量数据的精准性,旅客运输时能增加舒适性.由于SWATH船具有诸多优点,不少国内外学者对其进行了广泛而深入的研究.文献[5]中应用二维时域格林函数法对某高速双体船在斜浪中的运动响应与连接桥载荷进行了预报,验证了二维时域格林函数法的适用性.文献[6]中对“小水线面双体船实船”在斜浪中的参数激振问题进行分析,结果证明SWATH船在斜浪上的横摇不会导致纵摇和垂荡运动发生参数共振.文献[7-8]中用自行开发的一套基于三维面元法的预报程序对双体船与三体船进行了水动力与运动响应计算,计算结果与试验数据吻合良好,计算效率大约提高了3倍.文献[9]中分析了船舶尺度与主要参数对船舶耐波性的影响,然后通过不同模型的比较分析建立了耐波性预报模型.文献[10]中采用修正的切片法,并考虑其粘性效应,对穿浪双体船进行了频域分析,结果证明修正的切片法是可靠的.文献[11]中基于Rankine源法对单体船耐波性进行了预报,结果证明Rankine源法对单体船耐波性的预报是良好的.基于Rankine源法的小水线面双体船耐波性预报在国内研究目前较少,小水线面双体船的水动力性能比单体船更加复杂,导致其耐波性预测相对困难,而模型试验通常需要花费较多经费与较长的时间,故在小水线面船船型初步阶段采用合理的数值计算方法对其耐波性进行预报是合理可行的.
1 计算模型
1.1 Rankine源方法
文中所采用的是由挪威船级社开发的水动力分析软件Wasim,Wasim是基于三维Rankine源方法的时域计算软件,能够对航行中的船舶进行波浪载荷与运动响应计算.程序的求解采用的是势流理论,因此流体粘性的影响被忽略.Rankine源方法也叫简单格林函数法,是用来计算船舶兴波阻力的数值计算方法,它将均匀流替换为合模流[12].Rankine源方法优点在于计算简单,在考虑自由面非线性和定常势的影响的前提下,避免了不规则频率问题.
1.2 计算模型
双体船模型采用的坐标系如图1所示.x轴指向船舶航行方向,z轴竖直向上,并通过船舶的重心,y轴指向船舶左舷,该船主尺度与主要参数见表1.
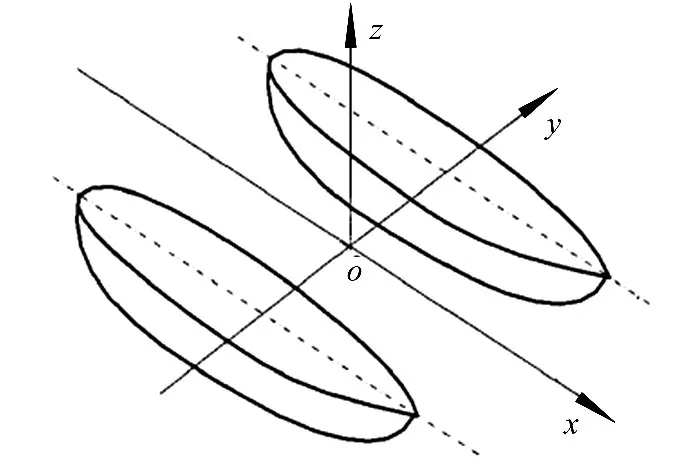
图1 小水线面双体船运动坐标系Fig.1 Reference frame of SWATH ship motions
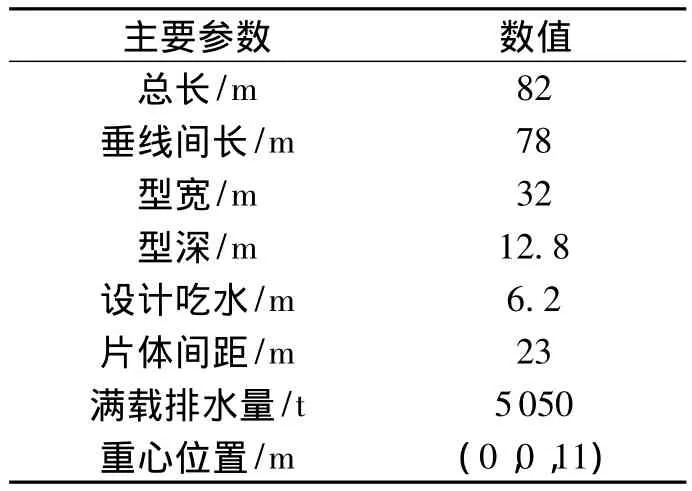
表1 主要参数Table 1 Main parameters
水动力分析软件Wasim已用于大量的船舶与海洋工程计算,计算结果也经过了几十年的工程实践和对比,其可靠性在中外文献中亦得到佐证,是行业内公认的权威水动力分析软件.
Rankine源格林函数不满足任何边界条件,因此必须在边界上划分网格,布置源汇来保证满足边界条件.在Wasim中输入船舶型值文件“*.pln”生成节段模型,然后程序会自动在船体表面与自由面生成网格.船体模型与自由面网格如图2,3.

图2 船体表面网格Fig.2 Surface grid of ship
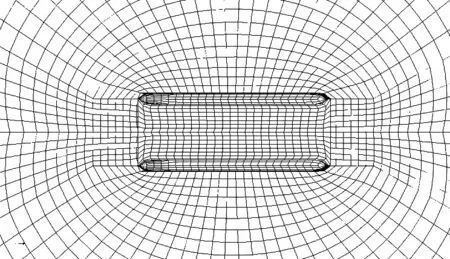
图3 船体模型与自由面网格Fig.3 Hull model and free surface grid
1.3 计算工况
选取4,5,6级3个典型海况时小水线面双体科考船的运动响应进行计算分析,定义7个浪向,分别为 180°(迎浪)、150°(艏斜浪)、120°(艏斜浪)、90°(横浪)、60°(艉斜浪)、30°(艉斜浪)和 0°(顺浪),航速设定为0,3,6,9 kn.
波浪采用JONSWAP波谱定义,具体参数见表2.

表2JONSWAP波谱参数Table 2 Wave parameters of JONSWAP spectra
2 计算结果与分析
2.1 无航速下运动响应分析
采用Wasim软件对不同有义波高、浪向角μ与航速下SWATH科考船的运动响应进行计算并统计分析,取部分稳定时间段的数据统计其垂荡Z1/3、横摇 φ1/3和纵摇 θ1/3有义单幅值,进行绘图与分析,由于工况较多,文中只取了部分典型工况进行分析(图4~6).
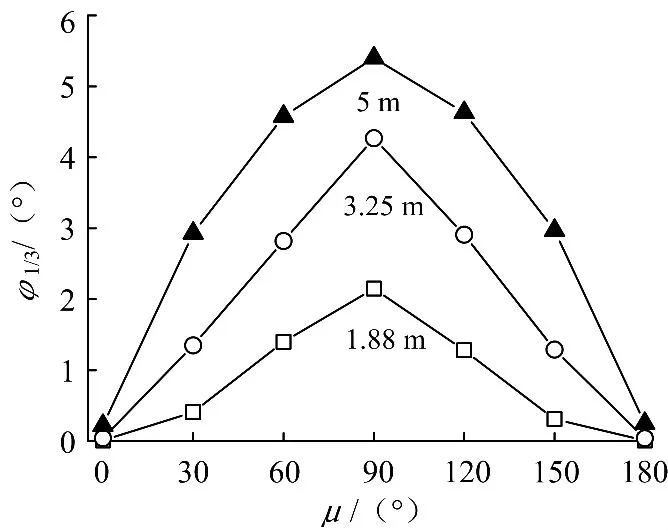
图4 无航速下横摇有义单幅值Fig.4 Significant single amplitude of roll at zero speed
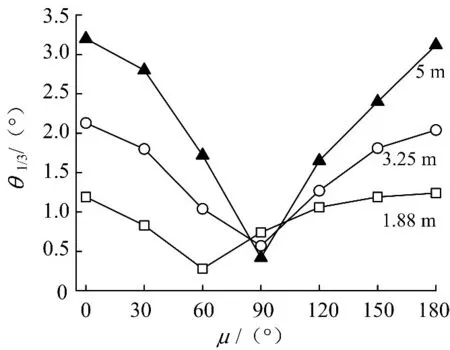
图5 无航速下纵摇有义单幅值Fig.5 Significant single amplitude of pitch at zero speed

图6 无航速下垂荡有义单幅值Fig.6 Significant single amplitude of heave at zero speed
由图4~6可看出:在无航速时,小水线面双体船横摇响应规律比较明显,最大横摇有义单幅值均出现在遭遇浪向为90°(横浪)时,最小值则出现在0°(顺浪)与180°(迎浪)时,且在同一遭遇浪向下横摇有义单幅值随着有义波高的增大而增大.
纵摇响应有义单幅值最小值基本在遭遇浪向为90°(横浪)时,1.88m有义波高时最小值在60°浪向,而最大值在遭遇浪向为0°与180°时.在同一有义波高下,随着遭遇浪向由0°变至180°,纵摇幅值先减小后增加.
船体垂荡响应的有义单幅值在有义波高为3.25m与5.00m时不同浪向下变化均较小;从图7无航速180°浪向下SWATH船垂荡响应时历曲线可得到此时垂荡周期约为8.7s,与有义波为1.88 m时波浪谱峰周期(8.8s)相近,导致有义波高1.88 m时有义单幅值显著增大,在遭遇浪向90°时出现极值.与波浪周期相近的垂荡固有周期导致垂荡响应易受到波浪周期变化的影响,故垂荡有义单幅值变化趋势及规律性并不如横摇与纵摇.同时5 m有义波高下,垂荡响应幅值突然增大,这是由于此时船体连接桥受到波浪砰击,船体受到更大的波浪外力引起的.

图7 无航速180°浪向下垂荡运动时历曲线Fig.7 Time history curve of heave motion at zero speed&180°wave direction
2.2 9 kn航速下运动响应分析
在航速为9 kn时,横摇、纵摇和垂荡响应的有义单幅值如图8~10.
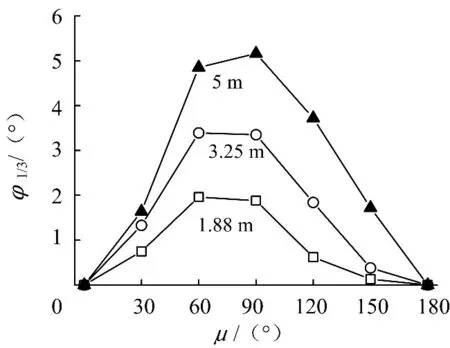
图8 9 kn航速下横摇有义单幅值Fig.8 Significant single amplitude of roll at 9 kn
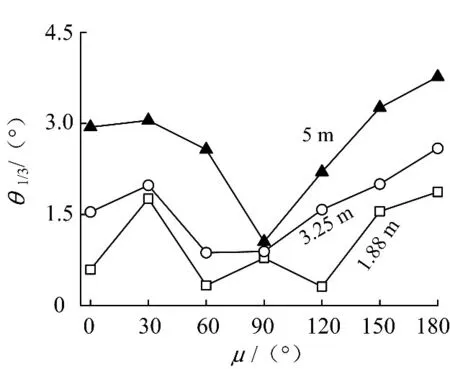
图9 9 kn航速下纵摇有义单幅值Fig.9 Significant single amplitude of pitch at 9 kn

图10 9 kn航速下垂荡有义单幅值Fig.10 Significant single amplitude of heave at 9 kn
由图8~10可看出:在9 kn航速时,横摇响应最大幅值出现在60°与90°,并不类似于无航速时仅仅出现在90°横浪时,最小值依旧出现在0°(顺浪)与180°(迎浪)时.
航速为9 kn时,船体纵摇响应在30°、150°和180°浪向时较大;相比无航速而言,30°浪向下的纵摇幅值有所增大.在有义波高为5m时,随着遭遇浪向由0°增至180°,纵摇幅值先减小后增加.
有义波高为1.88,3.25 m时,随着遭遇浪向由0°增至180°,垂荡响应有义单幅值在120°出现峰值,且随着有义波高的增加,相同遭遇浪向下的垂荡响应值增大;但当有义波高为5 m时,随着遭遇浪向的增大,垂荡响应增大,规律不同于1.88 m与3.25 m波高.
2.3 不同航速下运动响应分析
随着航速的变化,小水线面双体船与波浪的遭遇频率也随之改变,导致其耐波性也发生变化(表3).
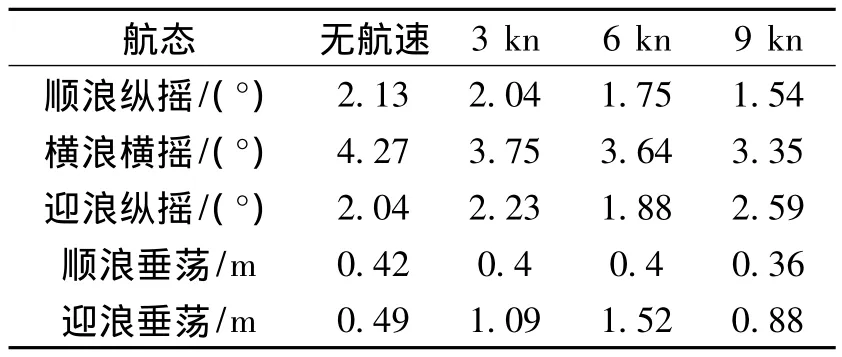
表3 有义波高3.25 m时运动响应值Table 3 Motion responses at 3.25 m significant waves height
从表中可以看出在顺浪航行时,随着航速的提高,纵摇是逐渐减小的,这与波浪遭遇频率有关,在顺浪航行时航速的增加导致波浪遭遇频率降低;垂荡在顺浪航行时变化较小,但在迎浪时有先增大后减小的趋势.在迎浪航行时纵摇的变化规律性不强.横浪横摇随着航速的提高同样是逐渐减小的.
3 结论
通过对不同工况下小水线面双体科考船运动响应值的计算与对比分析,得出以下主要结论:
1)无航速时,小水线面双体船横摇响应规律比较明显,横摇极大值出现在90°,纵摇极大值出现在0°与180°.共振效应使得垂荡显著增加;
2)较高航速时,横摇响应最大幅值出现在60°与90°浪向,SWATH 船在 30°、150°(斜浪)和 180°(迎浪)时纵摇明显要比其他浪向下运动幅值大;
3)波浪对连接桥的砰击会显著影响SWATH船的运动响应,使其运动响应出现不规则性且垂荡运动显著增大;
4)顺浪航行时航速对纵摇运动影响较大,其运动幅值随航速的提高而减小.
References)
[1] 吴有生,倪其军,葛纬桢,等.我国高性能船技术进展[J].船舶力学,2008,12(6):1014-1031.Wu Yousheng,Ni Qijun,Ge Weizhen,et al.Advances in technology of high performance ships in China[J].Journal of Ship Mechanics,2008,12(6):1014-1031(in Chinese).
[2] 龙文,周沙亚,邱辽原,等.小水线面双体船关键技术分析及应用展望[J].舰船科学技术,2012,34(2):4-15.Long Wen,Zhou Shaya,Qiu Liaoyuan,et al.Key technology and apply expection of SWATH ships[J].Ship Science and Technology,2012,34(2):4-15.(in Chinese)
[3] 史文强,于宪钊.国外小水线面双体船发展状况及趋势[J].舰船科学技术,2012,34(2):47-51.Shi Wenqiang,Yu Xianzhao.The development and future trend of foreign SWATH ships[J].Ship Science and Technology,2012,34(2):47-51.(in Chinese)
[4] 缪国平.近期船舶耐波性研究进展与展望[C]∥第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会.江苏无锡:海洋出版社,2012:31-44.
[5] 耿彦超,顾学康,汪雪良,等.高速双体船斜浪中运动响应及连接桥波浪载荷预报[J].船舶力学,2010,14(4):385-392.Geng Yanchao,Gu Xuekang,Wang Xueliang,et al.Prediction for motions and cross structure wave loads of high-speed catamaran in oblique seas[J].Journal of Ship Mechanics,2010,14(4):385-392.(in Chinese)
[6] 郭值学,肖袁根.小水线面双体船斜浪中运动的参数激振初探[J].中国造船,2010,51(3):230-233.Guo Zhixue,Xiao Yuangen.Preliminary study on parametric resonance of SWATH motion in oblique sea[J].Shipbuilding of China,2010,51(3):230-233.(in Chinese)
[7] Xu Yong,Dong Wencai.Fast seakeeping prediction method for a high speed catamaran advancing in waves[J].Journal of Ship Mechanics,2014,18(6):644-661.
[8] Xu Y,Dong Wencai.Valid hydrodynamic interaction regions of multiple ships advancing in waves[J].Journal of Hydrody Namics,2013,25(6):856-866.
[9] 王银.舰船方案设计中的耐波性预报模型研究[D].哈尔滨:哈尔滨工程大学,2012.
[10] 肖伟.穿浪双体船阻力和耐波性研究[D].湖北武汉:华中科技大学,2013.
[11] Heinrich Söding,Alexander von Graefe,Ould el Moctar,et al.Rankine source method for seakeeping predictions[C]∥OMAE Ronald W Yeung Honoring Sympousium on Offshore and Ship Hydrodynamics.Rio de Janeiro,Brazil:ASME,2012.
[12] Zhang Baoji.Shape optimization of bow bulbs with minimum wave-making resistance based on rankine source method[J].Journal of Shanghai Jiaotong University,2012,17(1):65-69.
