引入混合蛙跳搜索策略的人工蜂群粒子群算法

任 聪，葛洪伟，杨金龙，袁运浩

江南大学 物联网工程学院，江苏 无锡 214122

1 引言

Kennedy和Eberhart[1]于1995年提出了模拟鸟类觅食行为的粒子群优化算法（PSO），该算法是继遗传算法、蚁群算法之后，被提出的一种基于群体智能的新型优化算法。由于PSO算法能够解决大量非线性、多峰等复杂的优化问题，且具有易于实现、参数较少、并行等优点，因此，在科学和工程领域得到了广泛的应用。近些年来，国内外的许多学者致力于粒子群优化算法的研究，在算法性能改进和应用上取得了许多重要的成果。Shi和Eberhart[2]引入了惯性权重来提高算法的收敛速度。Jiao等人提出了在PSO中引入动态惯性权重的方法，用于提高算法的收敛速度[3]。Bergh和Engelbreeht[4]提出了一种协作粒子群优化算法，该算法通过不同种群之间的协作提高收敛精度。Jiang和Etorre[5]将混沌的方法引入到PSO中来避免早熟现象；Fan和 Zahara[6]提出了一种混合单纯形的粒子群优化算法，用于加快算法的收敛速度。文献[7]提出了在小生镜粒子群的最优值附近定向地产生粒子来提高算法的探索能力；文献[8]中引入人工蜂群搜索策略来解决粒子群算法易于陷入局部最优的问题。这些算法虽然在一定程度上提高了PSO算法的性能，但在收敛速度和避免早熟方面很难达到平衡，特别是在处理多峰函数优化问题时，收敛速度慢且易于陷入局部最优。

针对标准PSO在解决多峰问题时，易陷入局部最优解和算法收敛速度慢的问题，本文提出了一种引入人工蜂群和混合蛙跳搜索策略的粒子群算法（Artificial Bee Colony&Shuffled Frog Leaping Particle Swarm Optimization，ABCSFL-PSO）。首先，使用人工蜂群搜索策略来避免算法陷入局部最优，再使用蛙跳算法中更新最差适应度粒子的方法，加快算法的收敛速度，提高算法的搜索精度。实验结果表明，本文提出的算法能够显著提高粒子群算法的优化能力和运算速度。

2 标准PSO算法

标准PSO算法通过模拟鸟群飞行中的觅食行为，把鸟类个体看作随机的粒子，通过局部和全局最优来引导粒子飞向最优解。设在D维空间中，有N个粒子，每个粒子的位置xi=[xi1,xi2,…,xiD]，速度为vi=[vi1,vi2,…,viD]，其中，i=1,2,…,N，并设第i个粒子搜索到的历史最优位置为pi，整个粒子群搜索到的最优位置为pg，则粒子的位置和速度更新公式分别为：

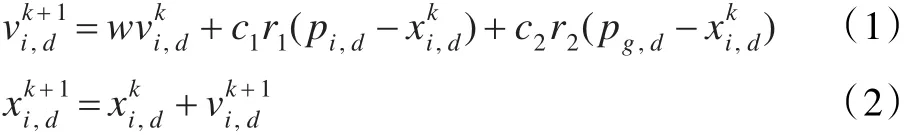
其中，w为惯性权值，c1和c2是学习参数，r1和r2为[0,1]之间的随机数。

3 引入蛙跳搜索策略的人工蜂群粒子群算法

3.1 人工蜂群搜索策略

Karaboga[9]在2006年提出了一种新的群体智能优化算法——人工蜂群优化算法（Artificial Bee Colony，ABC）。ABC主要通过模拟蜂群的采蜜行为来实现对求解问题的优化，它在解决多峰问题时具有优秀的探索能力，其探索能力主要通过式（3）函数实现：

3.2 混合蛙跳局部搜索策略

混合蛙跳算法SFLA（Shuffled Frog Leaping Algorithm）是由Eusuff和Lansey[10]于2003年提出的一种基于群体智能的优化算法。该算法具有较好的全局探索能力和较快的收敛速度，而且鲁棒性强等优点。

混合蛙跳算法搜索是通过如下公式每次更新适应度最差的粒子：

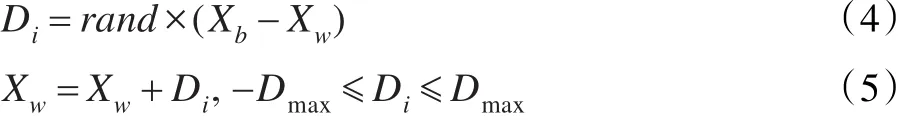
其中，i∈{1 ,2,…,N} ，Di为移动步长，Xb和Xw分别是种群中适应度最优的粒子位置和适应度最差的粒子位置，rand为[0 ,1]之间的随机数。

通过公式可以看出混合蛙跳算法（SFLA）是通过在全局最优粒子值引导下更新最差粒子值来搜索最优解。

3.3 ABCSFL-PSO算法

3.3.1 算法思想

由于人工蜂群搜索策略能够有效地避免陷入局部最优，而混合蛙跳算法通过更新最差适应度粒子来搜索最优解。受这两种搜索机制的启发，本文将人工蜂群和混合蛙跳算法的搜索策略结合，综合混合蛙跳算法在加速收敛和人工蜂群算法在避免局部最优方面的优势，提出了ABCSFL-PSO算法。

3.3.2 算法步骤

ABCSFL-PSO算法是采用文献[11]和文献[12]提出的混沌和反学习的方法进行初始化的，目的在于加快收敛速度和提高精度。算法步骤如下：

步骤1初始化参数，用混沌和反学习方法初始化粒子。

步骤2对每个粒子利用标准粒子群算法的公式（1）和（2）更新粒子速度和位置。

步骤3利用人工蜂群的局部搜索策略的公式（3）在全局最优解附近搜索新的解。

步骤4利用公式（4）和（5）计算适应度最差的Z个粒子，如果更新后粒子适应度改善则更新粒子位置，否则不更新粒子位置。

步骤5如果满足要求，则算法执行结束，并输出最优值；否则，转至步骤2继续执行。

3.3.3 算法伪代码

伪代码如下所示：

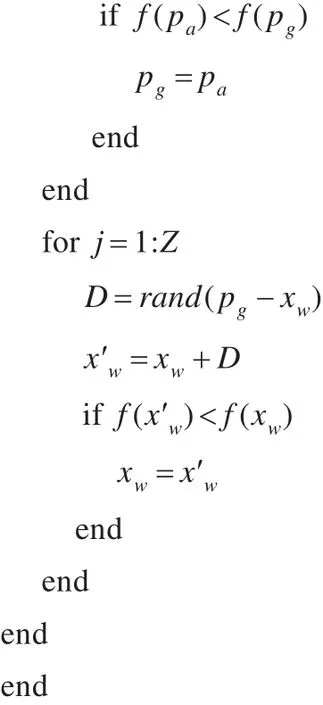
其中，K和M为固定值，p为最优值的位置，pg为全局最优粒子位置，vi为粒子速度，pi为第i个粒子的局部最优位置，xw为适应度最差的粒子位置。

4 仿真实验及结果分析

4.1 测试函数

为了证明ABCSFL-PSO算法的有效性，本文对文献[13]中的12个标准测试函数进行仿真实验。其中，Sphere函数和Rosenbrock函数是单峰函数，其他的均为多峰函数。表1为这12个标准测试函数的维数、搜索范围和最优解。

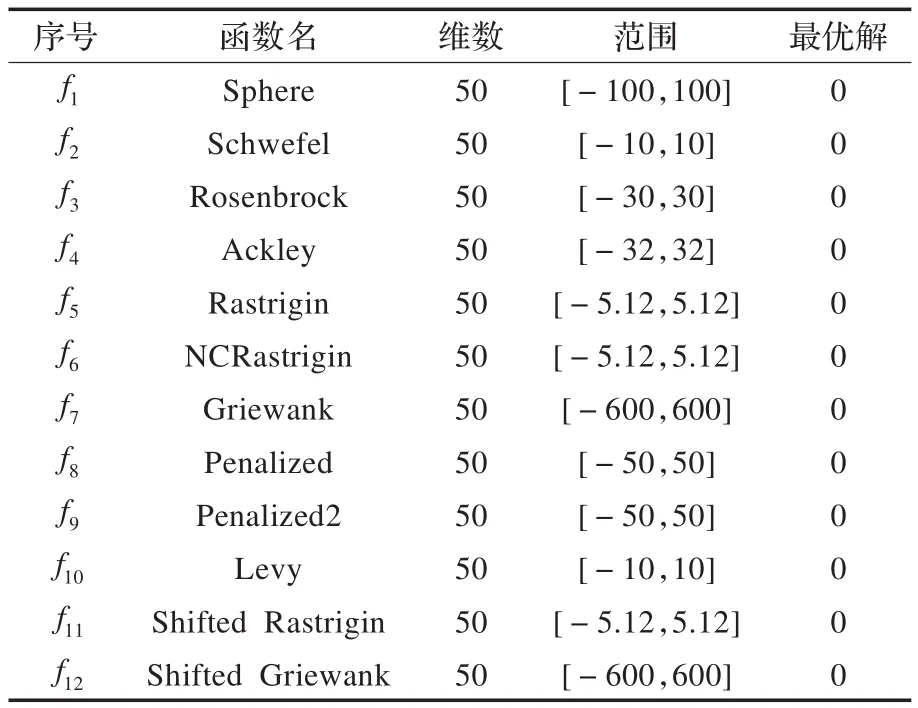
表1 测试函数的维数、搜索空间和最优值

4.2 实验及结果分析

为了检验本文所提出算法的有效性，将本文算法与文献[8]提出的PSOSW算法以及标准粒子群算法（BPSO）作比较。实验中，惯性权重w采用线性递减策略，最大值为0.9最小值为0，种群大小为30，维度D=50，K=300最大迭代次数为150 000次，采用Matlab2008a软件进行仿真实验。表2为3个算法在12个测试函数上进行50次独立实验并求平均值的结果，其中，平均适应度表示算法的寻优能力，标准方差表示算法的稳定性。通过实验结果可以得出，在平均适应度指标中，除f7外，其余的测试函数ABCSFL-PSO算法的搜索精度都高于其他对比算法，特别是在f1,f2,f5,f6这4个测试函数上搜索精度明显高于对比算法；在标准方差指标中，本文算法稳定性明显高于对比算法，特别是在f1表现的尤为明显。

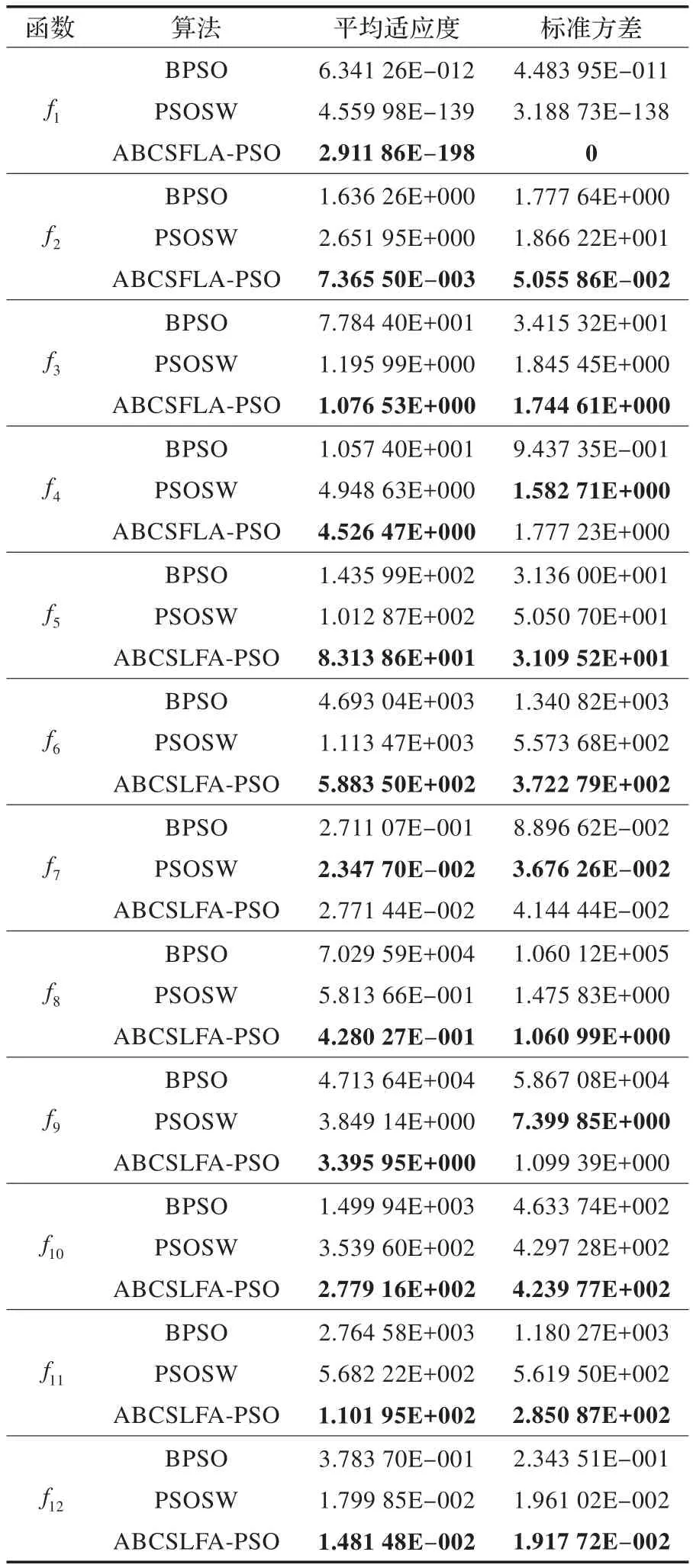
表2 运行50次的平均适应值和方差

图1～6展示了BPSO、PSOSW、ABCSFL-PSO三种算法在不同测试函数中的收敛曲线对比，以说明本文算法具有更快的收敛速度。从实验图可以看出，本文提出的ABCSFL-PSO算法收敛速度最快，不仅在收敛速度上具有明显的优势，同时也进一步提高了搜索精度。由于篇幅有限，本文只列举了具有代表性的6个测试函数对比图，在其他测试函数上也具有相似的性能。

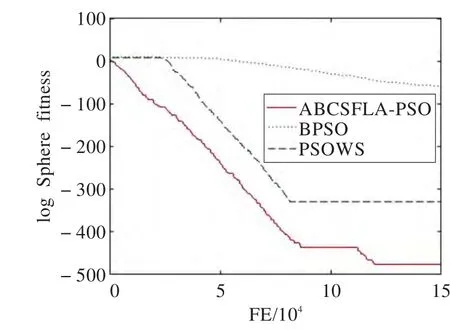
图1 f1函数的收敛性比比较

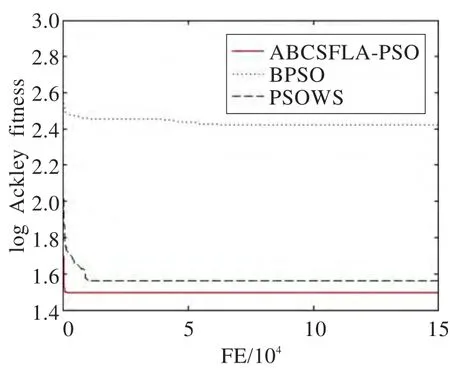
图2 f4函数的收敛性比比较

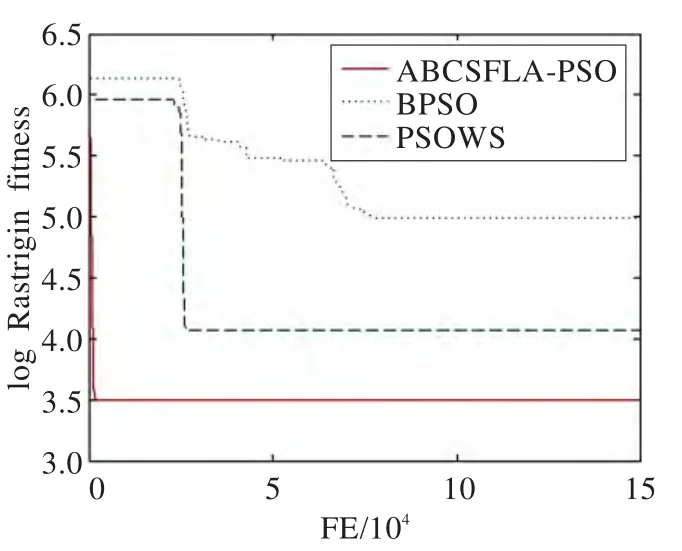
图3 f5函数的收敛性比比较

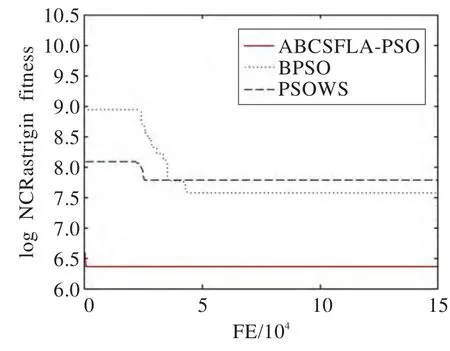
图4 f6函数的收敛性比比较

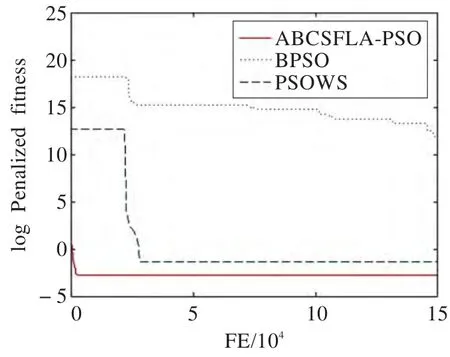
图5 f8函数的收敛性比比较

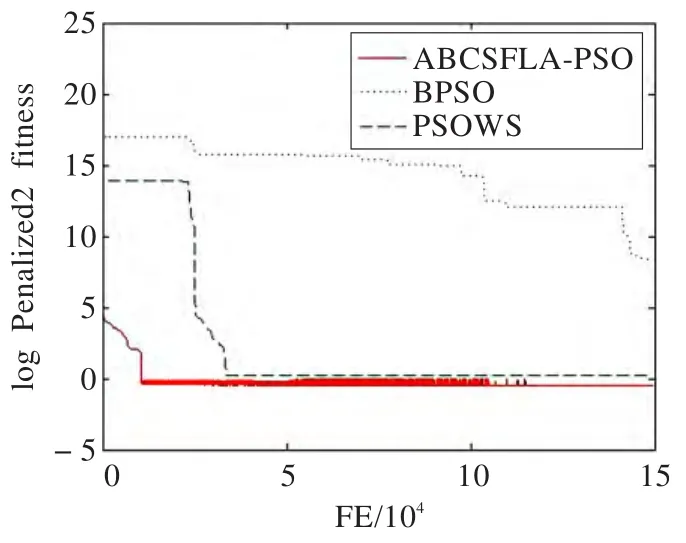
图6 f9函数的收敛性比比较

5 结束语

由于标准粒子群算法在寻优时存在收敛速度慢，易于陷入局部最优等问题，本文引入人工蜂群搜索策略和混合蛙跳算法搜索策略的粒子群算法。该算法通过人工蜂群搜索策略增强探索能力，再使用混合蛙跳算法的搜索策略加速收敛并进一步提高收敛精度。仿真实验表明该算法在收敛速度和探索能力上具有良好的性能，能够有效解决多峰函数问题。

[1]Kennedy J，Eberhartr C.Particle swarm optimization[C]//Proc of IEEE Int Conf on Neural Networks.Perth：IEEE Piscataway，1995：1942-1948.

[2]Shi Y H，Eberhart R C.A modified partile swarm optimizer[C]//Proceedingsofthe 1998 IEEE International Conference on Evolutionary Computation（CEC98），Anchorage，Alaska，USA，4-9 May 1998：69-73.

[3]Jiao B，Lian Z G，Gu X S.A dynamic inertia weight particle swarm optimization algorithm[J].Chaos Solitons&Fractals，2008，37（3）：698-705.

[4]Bergh F V D，Engelbreeht A P.A cooperative approaeh to partiele swarm optimization[J].IEEE Trans on Evolutionary Computation，2004，8（3）：225-239.

[5]Jiang C W，Etorre B.A hybrid method of chaotic particle swarm optimization and linear interior for reactive power optimization[J].Mathematics and Computers in Simulation，2005，68（1）：57-65.

[6]Fan S，Zahara E.Hybrid simplex search and particle swarm optimization for unconstratined optimization problems[J].European J of Operational Research，2007，181（2）：527-548.

[7]Qu B Y，Liang J J，Suganthan P N.Niching Particle swarm optimization with local search for multi-modal optimization[J].Information Sciences，2012，197：131-143.

[8]高卫峰，刘三阳，焦合华，等.引入人工蜂群搜索算子的粒子群算法[J].控制与决策，2012，27（6）：833-838.

[9]Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：Artificial bee colony（ABC）algorithm[J].J of Global Optimization，2007，39（3）：459-171.

[10]Eusuff MM，Lansey K E.Optimization of water distribution network design using shuffled frog leaping algorithm[J].Journal of Water Resources Planning and Management，2003，129（3）：10-225.

[11]Liu B，Wang L，Jin Y H，et al.Improved particle swarm optimization combined with chaos[J].Chaos，Solitons&Fractals，2005，25（2）：1261-1271.

[12]Rahnama S，Tizhoosh H R，Salama M M A.Oppositionbased differential evolution[J].IEEE Trans on Evolutionary Computation，2008，12（1）：64-79.

[13]Liang J J，Qin A K，Suganthan P N，et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Trans on Evolutionary Computation，2006，10（3）：281-295.