PAM-CRASH软件在地铁车碰撞分析中的应用
2015-02-27张霖,张婧
张 霖,张 婧
(长春师范大学工程学院,吉林长春 130032)
PAM-CRASH软件在地铁车碰撞分析中的应用
张 霖,张 婧
(长春师范大学工程学院,吉林长春 130032)
在地铁车辆碰撞分析中有限元求解软件得到普遍采纳。本文以某不锈钢地铁车辆为研究对象,借助通用显示有限元求解软件PAM-CRASH进行数值仿真,得到两列相同编组地铁车辆碰撞过程的变形趋势、能量曲线和撞击力曲线,进而评价车体的被动安全性能,并验证壳单元积分算法、沿单元厚度的积分点数和沙漏控制方法设置的合理性。合理的参数设置提高了数值分析结果的准确性,为地铁车辆的碰撞分析提供一定的理论依据。
地铁车辆;PAM-CRASH;数值仿真
耐撞性研究是地铁车辆现代化设计程度的一项指标。地铁车碰撞的多重非线性涉及以大位移为特征的几何非线性、以材料压缩变形为特征的材料非线性和以接触摩擦为特征的边界非线性[1]。研究此类问题的方法有实验测试和数值仿真。鉴于新产品研发的周期和成本,目前国内普遍采用数值仿真方法进行地铁车辆耐撞性研究。
随着数值仿真计算的深入,相关有限元软件PAM-CRASH、LS-DYNA和RADIOSS也逐渐成熟。而单元类型、控制参数和求解算法的不断完善提高了数值仿真的求解精度和求解效率。广泛使用的碰撞模拟软件PAM-CRASH属于新一代计算机三维碰撞模拟系统,强大的前处理系统和简明的后处理系统得到轨道车辆仿真领域的一致认可[2-4],控制参数和边界条件设置保证了大变形碰撞数值分析结果的准确性。
本文利用有限元软件的兼容性,基于某不锈钢地铁车的有限元模型,通过PAM-CRASH软件对两编组列车的碰撞过程进行数值分析。
1 基于PAM-CRASH的数值求解
1.1 碰撞数值仿真的理论基础
地铁车辆碰撞的多重非线性反映了碰撞过程数值分析的复杂性。考虑车体运动和变形方面,车辆碰撞过程涉及质量守恒方程、能量方程和运动方程。
质量守恒方程为
ργ=ρ0.
(1)
其中,γ为相对体积,ρ为当前质量密度,ρ0为初始质量密度。
能量方程为
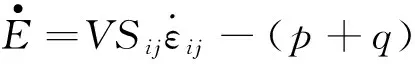
(2)
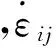
经单元离散后,可以得到有限元法求解车辆大变形碰撞之类的高度非线性动力分析的运动方程

(3)
其中,总体质量矩阵M为
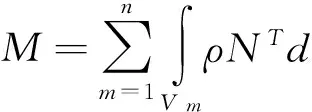

1.2 PAM-CRASH软件的控制参数问题
鉴于头车前端为大塑性变形区域,在计算中壳单元发生翘曲是必然的。对于壳单元的材料模型而言,PAM-CRASH软件在默认情况下采用Belytschko-Tsay积分算法,该算法是基于单元节点位于一个平面内的假设建立的,针对大塑性变形问题类型极有可能致使求解结果是不收敛的[5],本文采用考虑了单元翘曲刚度的Belytschil-Wong-Chiang积分算法。
鉴于沿壳单元厚度方向的应力分布呈现非线性特征,在单元厚度方向上增设积分点,增加求解的精准度;另一方面,沿单元厚度方向上积分点个数的增加也会致使求解时间增加。在保证求解精准度的前提下,力求减少求解时间,本文在沿单元厚度方向上设定的积分点个数为5。
四边形壳单元受缩减积分法的影响而产生沙漏模态,这种没有能量损耗的变形模态导致无序振荡的变形,降低结构刚度,数值求解结果的准确性因而降低。通常控制沙漏的方法有三种:基于向单元增加弹性刚度形式;基于向单元增加塑性刚度形式;粘性沙漏控制。鉴于头车前端结构是承担主要吸能的塑性大变形区域,PAM-CRASH软件通常采用的塑性刚度沙漏控制算法对于头车前端结构的处理仍显得较为刚硬,因而采用较高沙漏控制系数的粘性沙漏控制方法。
2 编组列车有限元模型的建立
本文研究的不锈钢点焊地铁车辆采用首尾头车、四节中间车的编组运行模式。在评价车体被动安全性能时,要求头车前端结构应为碰撞过程中发生塑性变形的主要区域。过粗的网格划分将致使求解结果失真,而单元尺寸过小会使求解时间以近似指数的方式增长。同时考虑到有限元模型的规模,编组列车的有限元模采用尺寸不同的网格划分,其中头车前端结构采用8mm的单元尺寸划分,头车其余结构采用20mm的单元尺寸划分,共计1074981个单元。中间车采用50mm的单元尺寸划分,共计10030个单元,编组列车有限元模型共计2899702个单元。车体有限元模型如图1所示。
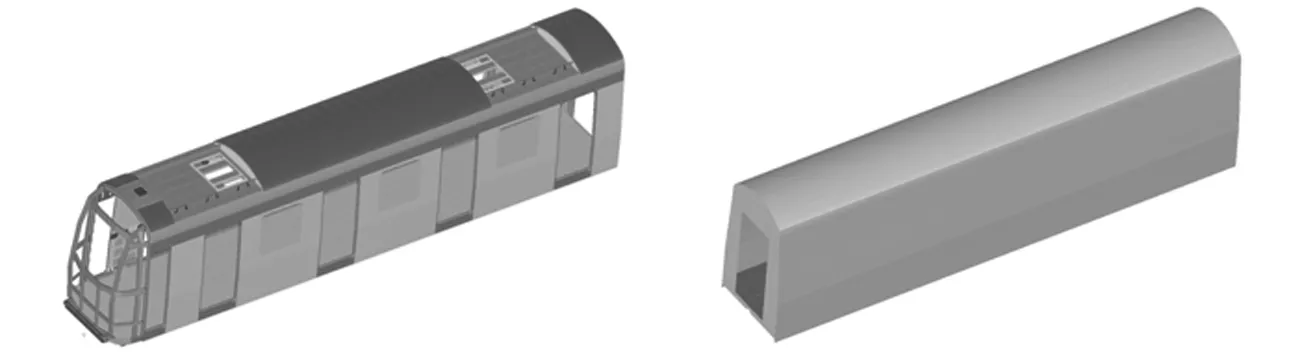
图1 车体有限元模型
3 编组列车的碰撞数值仿真
编组列车车体以15km·h-1的速度面对面发生碰撞,仅头车前端发生大塑性变形吸收冲击能量而客室区无变形,头车前端结构保障了客室区的安全,车体变形图如图2所示。
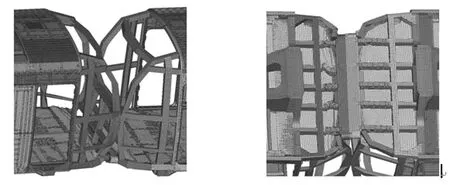
图2 车体变形图
列车车体以15km·h-1的速度面对面撞击时,碰撞总能量随时间变化的曲线如图3所示。可以看出,碰撞过程中系统总能量为2593.46KJ,且保持恒定。初始动能为2302.91KJ,由于沙漏导致的能量损失为290.55KJ,仅占系统总能量的11%。车体末动能为1323.35KJ,车体总吸能为1270.11KJ,满足碰撞过程中能量守恒定律,即系统总能量为末动能与总吸能之和(不考虑摩擦耗能)[6]。
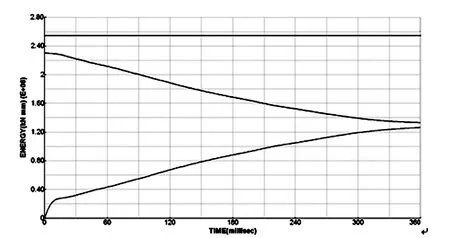
图3 车体能量-时间曲线
列车车体以15km·h-1的速度面对面撞击时,碰撞力随时间变化的曲线如图4所示。可以看出,在碰撞开始的20ms内撞击力迅速增大,在20ms到70ms逐渐下降,之后趋于稳定。在19ms时撞击力达到最大峰值756KN,满足联邦汽车安全标准。

图4 撞击力-时间曲线
4 结论
第一,综上对碰撞数值仿真理论基础进行了阐述,针对PAM-CRASH软件用于地铁车辆碰撞仿真分析的控制参数,依次讨论了壳单元的积分算法、沿单元厚度方向积分点数和沙漏控制方法,并针对本文研究对象确定了具体的控制参数。第二,利用PAM-CRASH软件完成该不锈钢点焊地铁编组列车碰撞有限元模型,通过对编组列车碰撞的数值仿真分析表明:车体前端区域发生大塑性变形吸收能量而客室区无变形,碰撞过程中撞击力变化规律正确且满足联邦汽车安全标准,车体被动安全性能良好。第三,编组列车碰撞过程中系统能量满足能量守恒定律,数值求解过程正确。沙漏导致的能量损失仅占总能量的11%,表明壳单元的积分算法、沿单元厚度方向积分点数和沙漏控制方法的设置合理,为地铁车辆的碰撞分析提供一定的依据。
[1]谢素明,兆文忠,闫学东.高速车辆大变形碰撞仿真基本原理及应用研究[J].铁道车辆,2001(8):1-4.
[2]田红旗,姚松.新型耐冲击铁路客车[J].铁道知识,2004(2):10-11.
[3]MarkusHecht.有轨电车和轻轨车辆的防碰撞性[J].国外铁道车辆,2005,42(5):39-41.
[4]贾宇.机车车体耐碰撞结构设计与碰撞仿真研究[D].成都:西南交通大学,2003.
[5]姚曙光,田红旗.高速不锈钢车体结构设计[J].铁道科学与工程学报,2008(1):72-75.
[6]LuG.耐碰撞车辆的能量吸收要求[J].国外铁道车辆,2006(3):8-13.
Application of PAM-CRASH in Crash Analysis of Subway Vehicle
ZHANG Lin, ZHANG Jing
(College of Mechanical Engineering, Changchun Normal University, Changchun Jilin 130032, China)
Explicit finite element solver software was universally adopted in the subway vehicle crashworthiness analysis. Take the stainless steel as subject, get the deformation trends, energy curve and force curve of collision course of two identical grouping subway vehicle by explicit finite element solver software PAM-CRASH, and evaluate passive safety performance of the vehicle, verify the reasonableness of shell element integration algorithm, the number of integration points along the thickness of the element and hourglass control method. The accuracy of numerical analysis was improved by abundant parameters, the accuracy of numerical analysis was improved by abundant parameters, and the theoretical basis of subway vehicle collision analysis was provided by the calculation results.
subway vehicle; PAM-CRASH;numerical simulation
2014-12-03
张 霖(1989- ),男,内蒙古呼伦贝尔人,长春师范大学工程学院车辆系助教,硕士,从事数值仿真研究。
U270.1
A
2095-7602(2015)04-0020-04
