关于廊坊市交通拥堵问题的数学模型的探究

徐秋丽，张召飞

(廊坊师范学院数学与信息科学学院，河北廊坊 065000)

关于廊坊市交通拥堵问题的数学模型的探究

徐秋丽，张召飞

(廊坊师范学院数学与信息科学学院，河北廊坊 065000)

本文通过调查廊坊市爱民道与新华路交口的车道设施、车流量及红绿灯的设置等情况，将各方面数据进行量化，分析造成道路交通拥堵的原因，针对现行方案的不足之处进行建模优化，即黄灯闪烁时间设置、红绿灯时间改进、信号灯设置调整、待行区域设置等方面的数学研究，得到更可行的交通缓解方案。

交通拥堵；微分方程；信号灯；待行区域

随着经济的快速发展、人们生活水平的日益提高，私家车的数量急剧增加，城市道路交通拥堵问题已经成为不容忽视的社会问题.就廊坊市区而言，交通拥堵问题已经影响人们的正常出行，尤其在上下班高峰时刻，多条道路拥堵严重，亟待得到有效的缓解.本文以廊坊市爱民道与新华路交口的交通现状为例，通过实地统计调查，分析交通拥堵的原因，应用数学建模的方法讨论缓解交通拥堵问题的办法.

1 问题分析

1.1 交通拥堵的概念

交通拥堵是指在一定时间内道路的承载能力不能满足车辆的通行需求，即道路上的车流量大于道路的最大车流量，超出部分的车辆滞留在路上的交通现象.

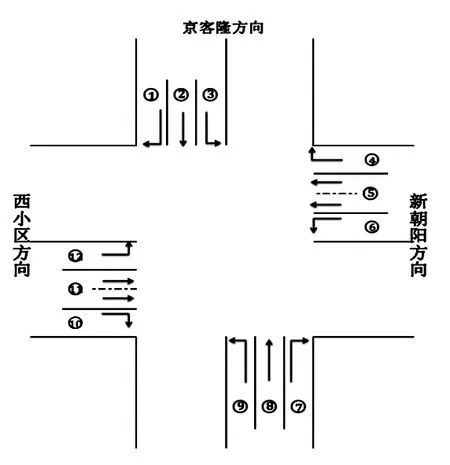
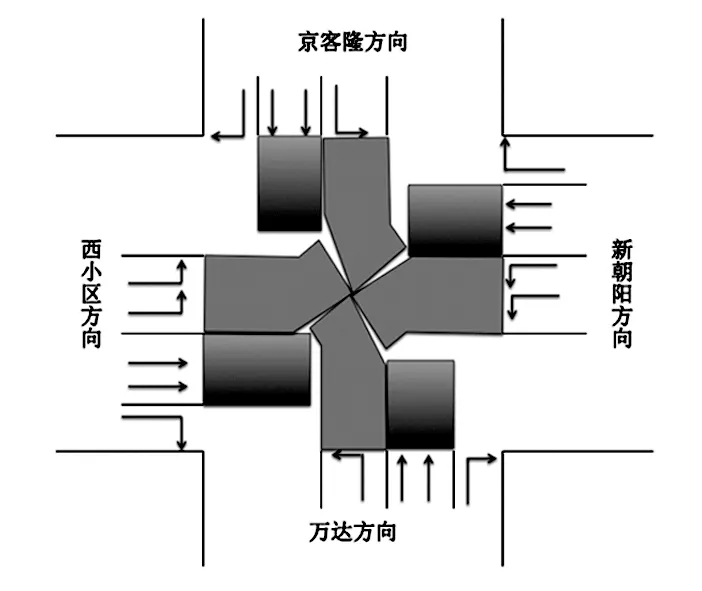
图1 路口相位图

1.2 交通现状调查

以爱民道与新华路交口为例，此路口采用红黄绿色信号灯控制，路口相位图如图1所示，交通高峰时刻的车流量统计数据如表1所示，一次信号灯变化周期内各信号灯时间如表2所示.

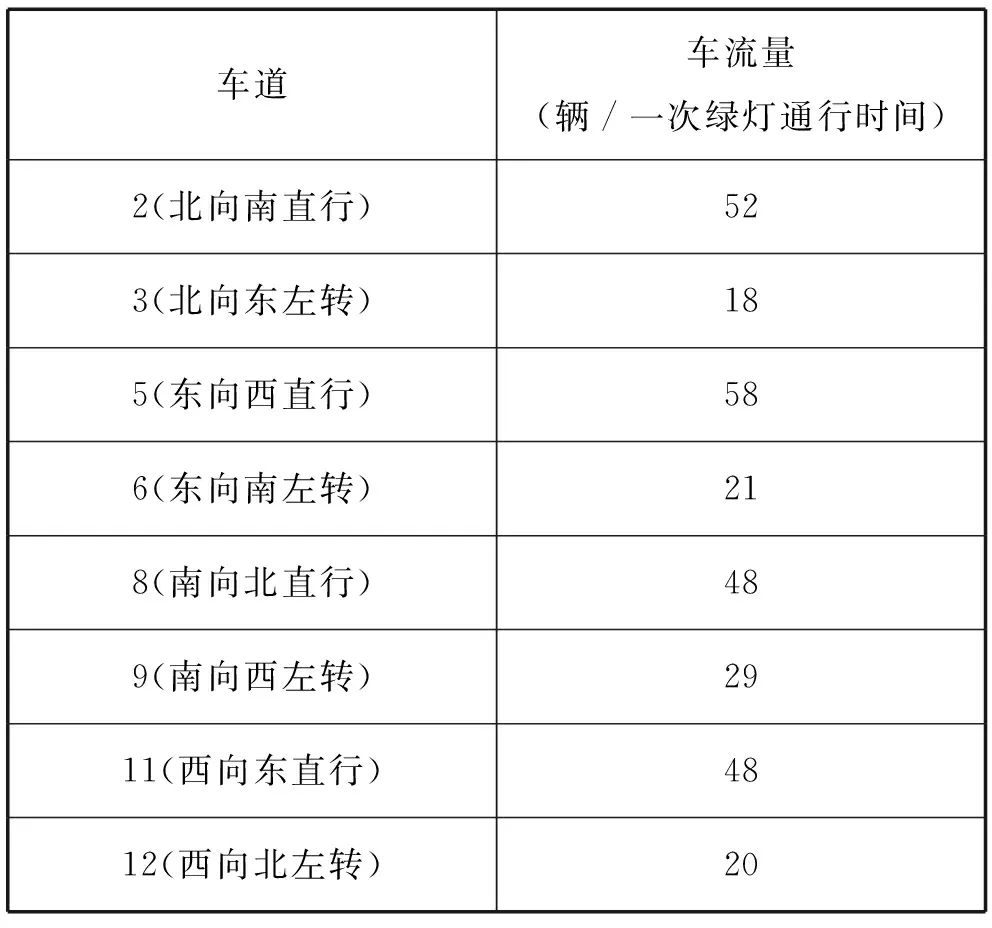
表1 车流量统计数据表

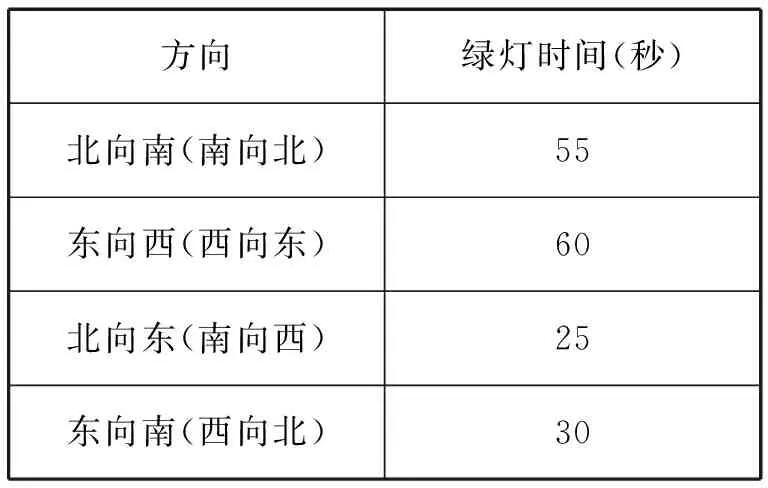
表2 一次信号灯变化周期内各信号灯时间示意表

1.3 交通拥堵原因分析

新华路是廊坊市南北中轴线，而爱民道是廊坊市东西中轴线，因此新华路与爱民道的交口可以被看作廊坊的最中心位置，附近商场、超市、公园等公共场所众多，势必会造成车流量大等交通困难.从调查情况来看，在上班早高峰期，由西向东车流量偏大，由北向南车流量偏大，而在下班高峰期，正好相反.造成交通拥堵的原因主要有以下几点.

(1)道路建设严重滞后，不能满足机动车数量的迅猛发展和日益增长的交通流量，以驶入爱民道西段为例，爱民道西段道路狭窄，从东向西两个直行车道的车辆，加之从北向西右转的车辆，一起涌入两个车道，势必会造成车速降低，有时为避免车辆刮蹭，甚至需要停车等待，从而导致由东向西方向大量车辆滞留，造成交通拥堵.

(2)公共交通发展滞后，首先是公共交通网络线不发达，大多数市民都感觉没有直达目的地的公交车，如果换乘公交车的话，短短20分钟的车程就会花掉40分钟甚至更长时间；其次是公交车间隔时间过长，两趟车的发车间隔最少需要11分钟，有时候甚至更长，使人感觉乘坐公交车出行多有不便.

(3)部分车辆与行人不遵守交通规则，若有行人闯红灯，势必造成车辆避让、车流缓慢，还有部分司机不按照道路标线行驶，占用非机动车道，驶入十字路口时会影响行人和骑车人，并入车流时会导致正常直行车辆行驶，从而影响一个绿灯周期内的车辆通过数量.

(4)信号灯设置有待改善，黄灯时间较短，会造成有些车辆因来不及停车而越过十字路口的停车线，但又由于红灯亮了而过不了路口，因而造成交通混乱.

2 模型建设

(1)假设车辆长度一致，车辆行驶速度一致；(2)假设道路状况良好，没有道路维修、交通事故、违章行驶；(3)不考虑天气影响和汽车状况的影响；(4)不考虑步行人流和非机动车流对交通的影响；(5)所有机动车辆同等对待，不区分私家车和公交车等；(6)不考虑右转车辆汇入车流对交通的影响.

3 数学模型

3.1 模型一，黄灯闪亮时间模型

文献[1]提出了十字路口黄灯闪亮时间的数学模型，简单阐述如下：

设m为汽车质量,f为刹车摩擦系数，x(t)为行驶距离，fmg为刹车制动力，则刹车过程满足下列运动方程：

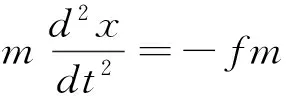
根据统计数据，驾驶员的反应时间约为2秒，汽车通过路口的行驶平均速度约为35km·h-1，路口长度为30m，车长为5m，沥青路面刹车摩擦系数为0.8，代入数据，得黄灯闪亮时间约为5秒.而在爱民道与新华路交口信号灯变化过程中，黄灯闪亮时间只有3秒.

3.2 模型二，红绿灯时间改进模型

首先，需要统计等候红绿灯的车辆，可以将超声波用于回声定位，利用测速仪测量汽车速度.

在距离信号灯x米处安装设备，超声波发出与返回的时间固定为t1，当有车辆经过时，t1会减小，利用计算机计算出这段时间为t0，利用测速仪测出这辆车的速度为v0，则该车的车长为L=v0·t0，这样可以求得每辆车的车长，利用以下程序可以算出这个车道上的汽车数量.

include

void main()

{

doublet,t0=**；//t0为没有车辆经过的时间；为有车辆经过时的时间

int;

for(i=0;;++)

{

scanf(“%if”,&t)；

if(t

j++;//有多少辆车

Printf(“%f”,t)；

}

}

停车后各个车辆之间存在车距，车距存在最小值，利用微分方程求最小车距如下.

设前车的位置为xn(t)，后车位置为xn+1(t)，则车距为

l(t)=xn(t)-xn+1(t).

(1)

由于前后车的速度差很小，视为相同，每辆车的刹车距离看作相同，司机的反应时间设为T，则后车的行驶距离为

(2)

设l*为停车后应该保持的距离，则有

(3)

将(1)代入(3)得到

人们等待5分钟左右，就会感觉厌倦，所以当第一辆车到达信号灯处，设后面有k辆车，那么第k辆车必须在5分钟内通过路口，第k辆车与信号灯的距离为S，则

S=kL+(k-1)l0.

设这段时间内信号灯改变了n次，每次红灯的时间为t，汽车行驶的速度为v1，则有S=v1[300-(n-1)t]，如果双向车道车流畅通，那么5分钟内，红灯和绿灯各150秒，此时根据车速可知5分钟内直行通过路程S0和车辆数量K0，所以当一个车道上车辆数量大于K0时，或者第一辆车后面车流长度大于S0时，只有自动减少红灯时间、增大绿灯时间，才能保证车辆顺利通过.

3.3 模型三，信号灯调整

前面已经分析造成交通拥堵的一个原因是右转车辆汇入车流时导致车速下降、通过能力降低，这一问题可以通过调整信号灯得以改善，参照路口相位图，将红绿灯进行调整如表3所示.

表3 红绿灯调整表

上述信号灯的调整避免了右转车辆汇入直行车流造成通行能力下降的问题.

3.4 模型四，待行区域设置模型

爱民道与新华路交口，路口信号灯变化规律为：南北直行绿灯；南向西、北向东左转绿灯；东西直行绿灯；东向南、西向北左转绿灯.在车辆直行时刻，左转车辆进入待转区域，当直行信号灯变红，左转信号灯变绿，可以有效地提高左转车辆数量.通过实地调查测算，发现当车辆由南向西、北向东左转时，接下来信号灯的变化应该是东西直行绿灯，而此时，东西方向可以在停止线前面设置待行区域，每个方向的直行待行区域长度可以达到7米左右，具体设置如图2所示，而行车安全性可以通过有效控制信号灯来保证，有效地提高直行车辆通过数量.

图2 模型四图例

4 模型评价

在模型一中，综合考虑了驾驶员的反应时间、车长及摩擦系数等多种因素，结合物理学和微分方程的知识，使得黄灯闪亮时间从理论上更准确，但没有考虑到车辆速度的变化等因素，从而使黄灯闪烁时间从实际上看没有那么精确.

在模型二中，在一定程度上考虑了驾驶员的主观感觉，尽可能地将可以通过的路线疏通，但忽略了行人和右转车辆的影响，同时此模型无法解决双向同时拥堵问题.

在模型三中，通过对信号灯的调整，减少了右转车辆对直行车速的影响，在一定程度上提高了路口的通行能力.

在模型四中，通过设置待行区域，可以有效地提高直行路口通过数量，但在实际操作过程中要注意交通安全，将待行区域的长度设置在安全范围内.

以上各种模型只能缓解交通拥堵，并不能从根本上解决这一城市难题，最根本的办法是加强城市的道路建设，大力发展公共交通事业，提倡公交出行.

[1]马锐.十字路口黄灯闪亮时间的数学建模分析[J].云南民族大学学报,2004,13(4):302-304.

[2]王秀良,乔木.十字路口黄灯时间及困境区域的数学模型研究[J].武汉理工大学学报,2011,35(5):896-900.

[3]韩维信,杨奇.城市道路交通发展规划的数学模型[J].数学的实践与认识,2002,32(6)：881-884.

[4]姜启源,谢金星.数学建模[M].北京:高等教育出版社,2003.

An Exploration on the Mathematical Model of Traffic Congestion in Langfang

XU Qiu-li, ZHANG Zhao-fei

(Mathematical and Information College, Langfang Teachers University, Langfang Hebei 065000, China)

By investigating the lane facilities, vehicle flow and signal lamp setting at the junction of Aimin Road and Xinhua Road in Langfang, this paper took all aspects of data to quantify, analyzed the reasons of causing traffic congestion, and then optimized the model for the inadequacies of the current program. Through setting the flashing time of yellow light, adjusting the time of traffic lights and setting waiting areas, etc., we got a more feasible traffic mitigation plan.

traffic congestion; differential equations; signal lights; waiting areas

2015-02-13

廊坊市科技局项目(2014011031)。

徐秋丽(1977- )，女，黑龙江青冈人，廊坊师范学院数学与信息科学学院讲师，硕士，从事应用数学研究。

O29

A

2095-7602(2015)04-0012-05