双移民两性分支过程的极限性质

刘 宣

(福州大学阳光学院基础部，福建福州 350015)

双移民两性分支过程的极限性质

刘 宣

(福州大学阳光学院基础部，福建福州 350015)

考虑同时带个体移民和配对单元移民的两性分支过程，称为双移民两性分支过程。本文首先介绍这种两性分支过程模型，然后讨论过程的状态性质，在一定的条件下得到过程的正常返性，最后研究第n代每个配对单元平均增长率的极限行为并利用马氏链的相关结论给出过程的极限性质。

两性分支过程；移民；马氏链；正常返

生物国普遍存在两性关系.为了更好地研究此类物种在进化过程中数量的变化规律，D.J.Daley在Galton-Watson分支过程的基础上于20世纪60年代引入了两性Galton-Watson分支过程[1].随后，此模型获得了广泛关注和深入研究[2-7].由文献[1]可知初始模型没有考虑移民的情况，而现实中这种现象是普遍存在的.因此不少学者开始考虑带有移民的两性分支过程，如文献[2-4]研究了只带有个体移民的两性分支过程，文献[5-6]研究了只带有配对单元移民的两性分支过程，然而实际情况往往是个体移民和配对单元移民会同时发生，如人口在地区之间的迁移.为了更精确地描述移民的情况，本文提出了同时带个体移民和配对单元移民的两性分支过程，简称双移民两性分支过程，模型如下：

Z0=N≥1,

(1)

Zn+1=L(Fn+1,Mn+1)+In+1,n=0,1,2,…,i=0,1,2，….

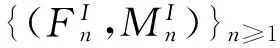
一般假定配对函数满足上可加性，即对n≥2,有

主要结果及证明

设S为模型(1)的状态空间.

引理1 对双移民两性分支过程，若P[L(f01,m01)=0]<1,P(I1=0)<1,则对任意的t∈S,存s∈S,s>t使得0可达s.

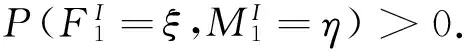
(x0,y0)=(ξ,η),(xn+1,yn+1)=(α,β)kn+(ξ,η),k0=0,kn+1=L(xn,yn)+γ.

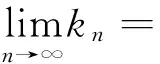
故对任意的正整数n，0可达kn.

证明 由已知条件，可得

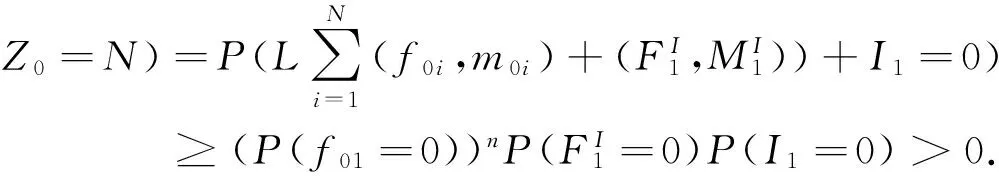
所以0∈S.由00,P(Zn+1=0)>0且存在正整数k0使得P(Zn=k0)>0.于是

所以

因此0为常返状态.又因为

所以0为此过程的正常返状态.

定理1 对双移民两性分支过程，若P[L(f01,m01)=0]<1,00,p00>0,则{Zn}n≥0是一不可约非周期马尔科夫链.

证明 受文献[2]启发，首先证明对任意的t∈S,可一步到达0.因为00,p00>0,由

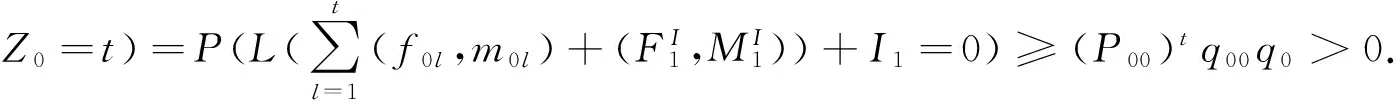
可知对任意的t∈S,可一步到达0.然后证明若某一状态t可达另一状态u，则状态0也可达状态u.若t可达u，那么存在正整数n，使得P(Zn=u|Z0=t)>0.再由引理1知，存在s∈S,s>t,使得0可达s,另外有

综上所述，可知状态空间S仅由一本质非周期类(0类)和一些非本质状态(一步可达0)构成，故{Zn}n≥0是一不可约非周期马尔科夫链.最后由引理2知，{Zn}n≥0是一不可约非周期正常返马尔科夫链，即遍历马氏链.

定理2 对双移民两性分支过程，若P[L(f01,m01)=0]<1,00,p00>0,则{Zn}n≥0依分布收敛到一个取值为正的有限的随机变量.

证明 由定理1和遍历马氏链的性质即可证明.

证明 根据已知条件，由强大数定律知

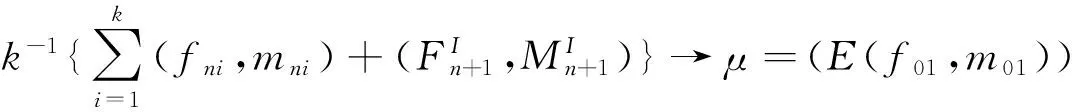
由配对函数的上可加性知其是非降函数，类似文献[7]中引理3的讨论得到，

又因为

再由引理3知过程是正常返的，所以{Zn}n≥0依分布收敛到一个取值为正的有限的随机变量.

[1]Daley,D.J.ExtinctionconditionsforcertainbisexualGalton-Watsonbranchingprocesses[J].Z.Wahrscheinlichkeitsth,1968(9):315-322.

[2]Gonzalez,M.,Molina,M.,Mota,M.LimitbehaviourforasubcriticalbisexualGalton-Watsonbranchingprocesswithinmigration[J].Statist.Probab.Lett,2000(49):19-24.

[3]LuZhunwei,ChenHongfang.LimitBehaviorforaClassofBisexualGalton-WastonBranchingProcesseswithImmingrationinRandomEnviromments[J].JournalofTaiyuanUniversityofTechnology(InChinese),2010,41(6):779-782.

[4]SongMingzhu.TheLimitPropertiesoftheBisexualbranchingprocesswithPopulation-sizedependentImmingrationinRandomEnvironments[J].ActaMathematicaeApplicataeSinica(ChineseSeries),2012,25(3):667-671.

[5]Gonzalez,M.,Molina,M.,Mota,M.OnthelimitbehaviourofasupercriticalbisexualGalton-Watsonbranchingprocesseswithimmigrationofmatingunits[J].StochasticAnal.Appl,2001(19):933-943.

[6]MaShixia,XingYongsheng.TheasymptoticpropertiesofsupercriticalbisexualGalton-Watsonbranchingprocesseswithimmigrationofmatingunits[J].ActaMathematicalScienti,2006,26B(4):603-609.

[7]Daley,D.J,Hull,D.M.andTaylor,J.M.BisexualGalton-Watsonbranchingprocessgewithsuperadditivematingfunctions[J].J.Appl.Prob,1986(23):585-600.

The Limit Properties of the Bisexual Branching Process with Two Kinds of Immigration

LIU Xuan

(Foundation Department,Fuzhou University Sunshine College, Fuzhou Fujian 350015, China)

In this paper,we consider a bisexual branching process with individual immigration and unit immigration called two types of immigration.First we introduce this bisexual Galton-Watson branching processes, then discuss the properties of its state space and obtained positive recurrent in some conditions. Finally thelimit behaviour of the mean growth rate per mating unit is studied and the limit properties for the process is investigated by using relevant conclusions of Markovchain.

bisexual branching process;immigration;markovchain;positive recurrent

2014-12-23

福建省教育厅中青年教育科研项目(JB13262)。

刘 宣(1982-)，男，湖南耒阳人，福州大学阳光学院基础部讲师，硕士，从事随机过程研究。

O211

A

2095-7602(2015)04-0005-04