基于径向基函数神经网络的波束形成算法
2015-02-27张宝军卢梦怡陈治清曹雅萍
张宝军, 卢梦怡, 陈治清, 曹雅萍
(西安邮电大学 电子工程学院, 陕西 西安 710121)
基于径向基函数神经网络的波束形成算法
张宝军, 卢梦怡, 陈治清, 曹雅萍
(西安邮电大学 电子工程学院, 陕西 西安 710121)
提出一种基于径向基函数(RBF)神经网络的波束形成算法。针对最小方差无失真响应(MVDR)算法,由接收信号的协方差矩阵计算其权矢量;将协方差矩阵以列向量的形式输入RBF神经网络,对其加以训练,使之逼近MVDR算法的权矢量;将训练好的RBF神经网络用于波束形成中,对不同角度的接收信号,RBF神经网络可自适应地输出相应权矢量。仿真结果表明,基于RBF神经网络的波束形成算法能快速逼近任意波束算法的权矢量,波束赋形效果良好,与已有波束形成算法相比,可降低算法复杂度,减少计算量。
波束形成算法;最小方差无失真响应算法;人工神经网络;RBF神经网络
波束形成作为阵列信号处理的关键技术之一,在雷达、通信、医疗和声呐等领域都有广泛应用[1]。常见波束形成算法主要有最小均方误差(Least mean square, LMS)算法[2]、采样矩阵求逆(Sample matrix inversion, SMI)算法[3]和最小方差无失真响应(Minimum variance distortionless response, MVDR)算法[4]。LMS算法无法平衡收敛速度和稳态误差之间的矛盾;当信噪比升高时,SMI算法鲁棒性能会有所下降;MVDR算法需要矩阵求逆,计算量大,不适合最优权矢量实时性更新要求。
RBF神经网络[5]是一种前向反馈网络,具有逼近快速、结构简单、容错和归纳能力强的特点,被广泛应用于通信信号处理和波束形成领域。
本文拟基于RBF神经网络对MVDR算法加以改进,即采用RBF神经网络逼近MVDR算法权矢量,完成从阵列协方差矩阵到最优权矢量这一非线性映射过程,用RBF神经网络代替原先MVDR算法的矩阵求逆过程。
1 信号模型
考虑N元等距线阵,阵元间距为d,且假设阵元均为各向同性阵元,远场处有一个期望信号和P个窄带干扰以平面波入射,到达角度分别为θ0和θk(k=1,2,…,P),阵列接收的快拍数据为[6]
X(t)=AS(t)+n(t)。
其中
X(t)=[x1(t),x2(t),…,xN(t)]T,
A(t)=[a(θ0),a(θ1),…,a(θP)],
S(t)=[s0(t),x1(t),…,sP(t)]T,
n(t)=[n1(t),n2(t),…,nN(t)]T,
分别为阵列数据向量、阵列流形矩阵、信号复包络向量和阵列噪声向量,sk(t)为第k个信源的复包络,而
a(θk)=[1,ejβk,…,ej(N-1)βk]T
为第k个信源的导向矢量,其中
阵列输出信号为
y(t)=WHX(t)。
其中加权矢量
W=[w1,w2,…,wN]T。
阵列响应为
F(θ)=WHa(θ)。
其中
方向图增益为
根据实际情况,权矢量W的算法略有不同,常用的是MVDR算法,满足最小噪声方差准则,当期望信号和方向都已知时,使得输出功率最小。最小噪声方差准则的输出功率可表示为
Pout=E[|y(t)|2]=E[WHRi+nW]。
其中
Ri+n=E[Xi+n(t)Xi+n(t)]
为干扰加噪声信号的协方差矩阵。利用拉格朗日乘子法可得
若将干扰加噪声协方差矩阵改为信号和干扰加噪声协方差矩阵,就是最小功率无失真响应(Minimum Power Distortionless Response,MPDR)波束算法。
2 波束形成的RBF神经网络
权矢量是协方差矩阵的一个非线性函数,求解过程需要用到协方差矩阵求逆运算,其运算量与阵元数呈平方关系,因此MVDR算法计算量大,会给实时运算带来困难。考虑到RBF神经网络是一种并行结构,可以快速逼近非线性函数的特性,因此采用RBF神经网络来解决这一问题。
在波束形成中的RBF神经网络如图1所示。
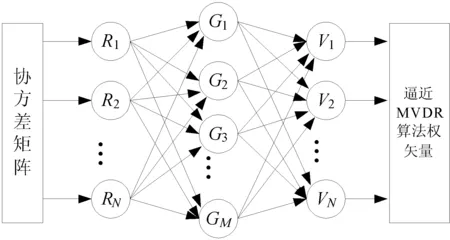
图1 RBF神经网络设计
假设阵元数N,则输入层有N个节点、隐层有M个节点、输出层有N个节点。RBF神经网络的输入层信号为阵列接收信号的协方差矩阵R1,R2,…,RN。RBF神经网络隐层的径向基函数采用高斯函数,隐层输出信号表示为[7]
其中σj表示第j个神经元节点的高斯函数方差,而
R=[Ri]T,c=[cji] (i=1,2,…,N),
后者为第j个神经元节点的高斯函数中心。
RBF神经网络输出层表示为
其中Z11,Z12,…,ZMN表示隐层到输出层上的连接权值,V1,V2,…,VN表示网路的输出,而VN就是逼近后的MVDR算法权矢量。
假设阵列接收信号的角度θ从-90°到90°变化,取间隔为1°,可以产生181对训练样本数据,取一部分训练样本用来训练RBF神经网络。采用K-均值聚类算法[8]把训练样本分成k类,高斯函数中心c(k)取第k类的聚类中心矢量,取该中心与其他聚类中心的最小距离为高斯函数方差σ(k)。接着对RBF神经网络进行学习,确定隐层到输出层的连接权值,就此确定RBF神经网络。
RBF神经网络学习步骤可描述如下(图2)。
步骤2采用快拍数L求出协方差矩阵R,计算MVDR算法权矢量WMVDR。
步骤3将R提取实部虚部Rre+im,将WMVDR提取实部虚部Wre+im,产生(Rre+im,Wre+im)训练样本对,将Rre+im作为RBF网络的输入信号,逼近Wre+im。
步骤4得到网络输出,即为逼近后的MVDR算法权矢量Vre+im,并转变为复数VRBF。
步骤5将Vre+im与期望权矢量WMVDR进行比较,计算误差e=‖WMVDR-VRBF‖2,如误差e大于给定误差范围,则n=n+1,跳回步骤1,否则跳到步骤6。
步骤6停止循环运算,RBF网络学习结束,确定隐层到输出层的连接权矢量。
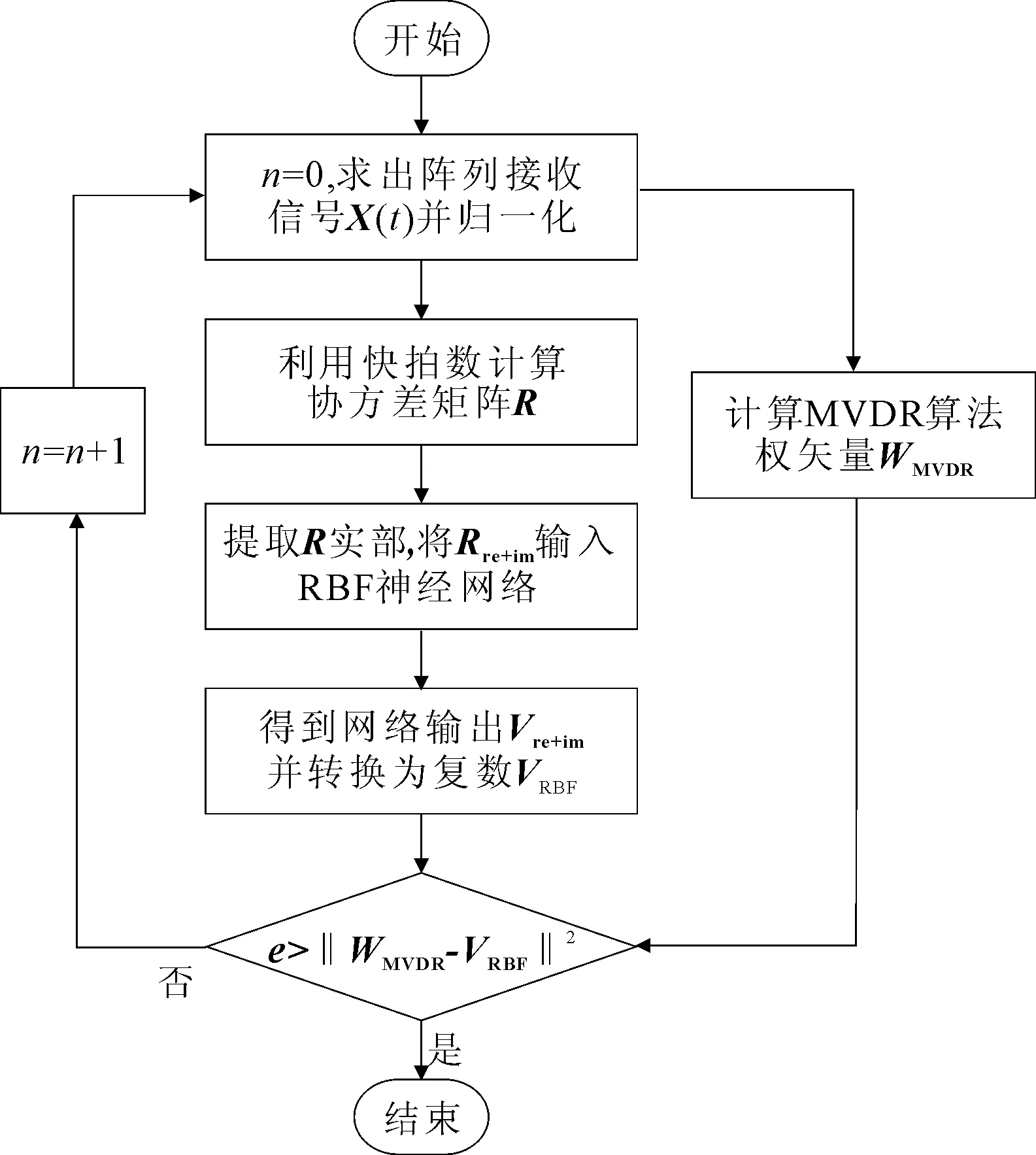
图2 RBF神经网络学习流程图
经过训练学习之后的RBF神经网络,将获得的MVDR算法的最优权矢量存储起来,之后RBF神经网络就可以工作了。
改进算法的整体设计方案如图3所示。
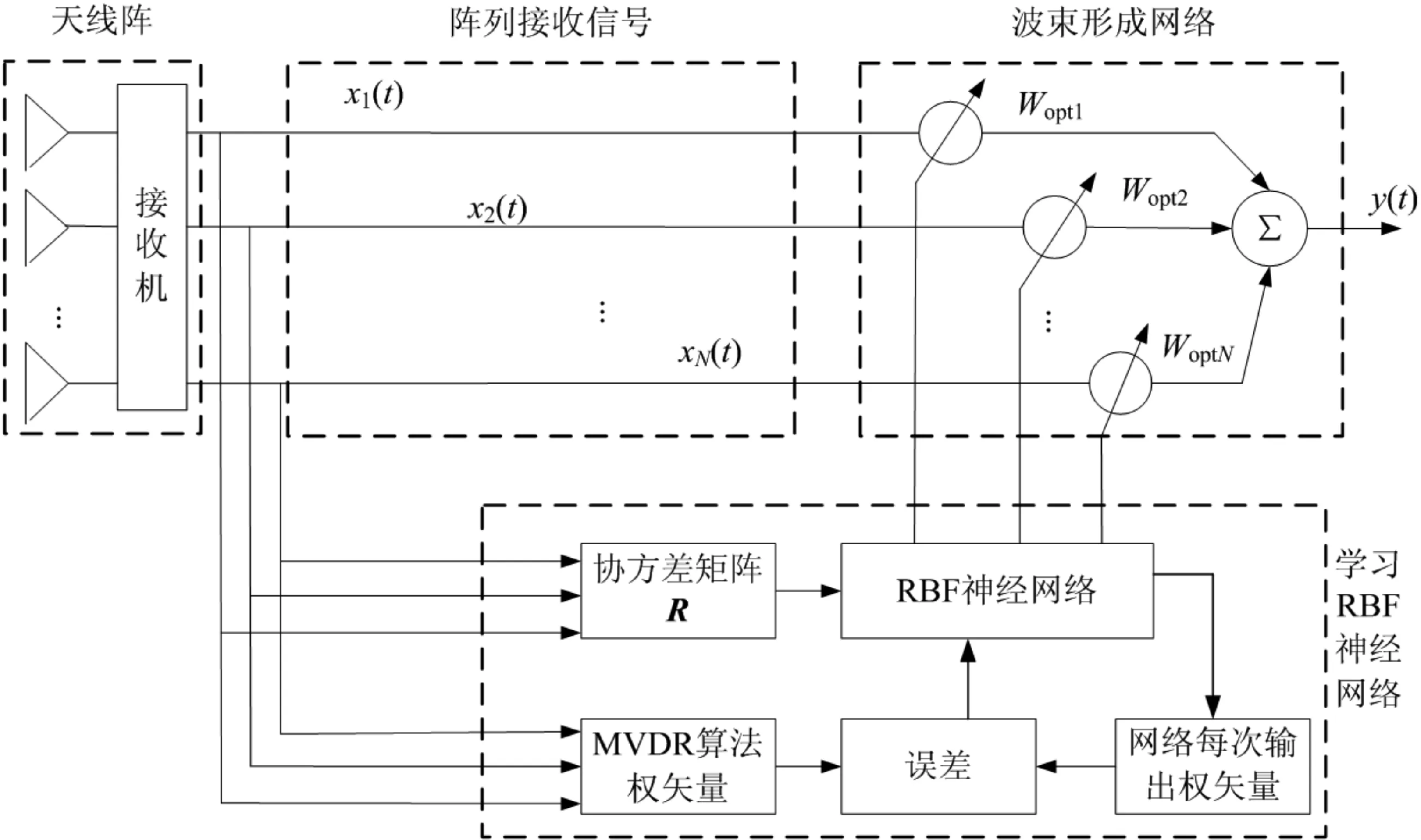
图3 改进算法设计方案
当有另一部分训练样本作为信号数据输入RBF神经网络时,网络会根据输入信号的不同角度自适应的输出最优权矢量,因此RBF神经网络不仅能得到最优权矢量输出,还可以避免上行链路的DOA估计[9],由此减少计算量。
3 仿真实现
实验18阵元的等距线阵,期望信号入射角度为0°,信号功率10 dB,干扰角度为-50°和50°,噪声功率0 dB,快拍数1 024时归一化后的阵列响应方向图如图4所示,实线表示MVDR算法方向图,虚线表示RBF神经网络逼近方向图。
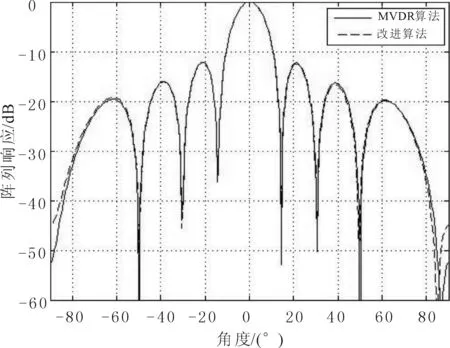
图4 MVDR算法和改进算法对比
MVDR算法与改进算法的权矢量比较如表1所示。
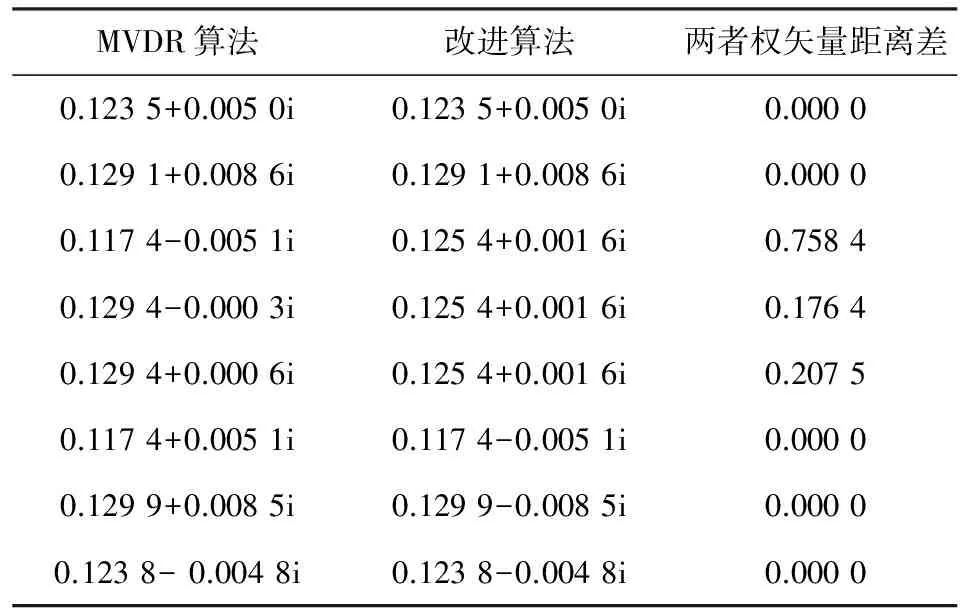
表1 MVDR算法与改进算法的权矢量对照
由图4和表1可以看出,RBF神经网络有着局部逼近的功能,能快速逼近MVDR算法权矢量,形成阵列方向图。
实验28阵元的等距线阵,期望信号入射角度为0°,信号功率10 dB,干扰角度为20°和60°,噪声功率0 dB,快拍数1 000时归一化后的阵列响应方向图如图5所示,其中实线表示MPDR算法方向图,虚线表示RBF神经网络逼近方向图。
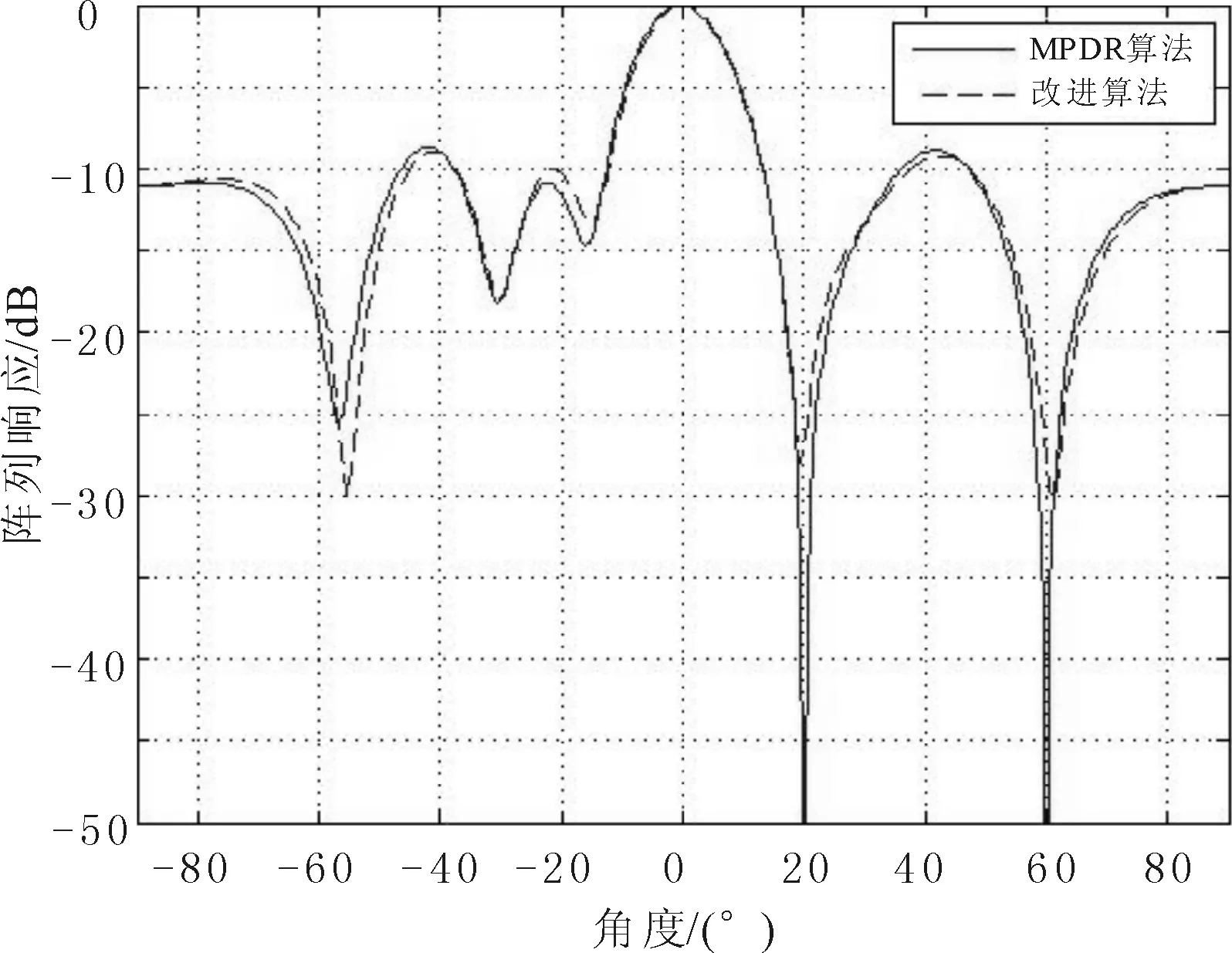
图5 MPDR算法和改进算法对比
由图5可见,针对不同算法,RBF神经网络都依然可以快速逼近权矢量,形成阵列方向图。
4 结语
针对MVDR算法在权矢量求解过程中计算量大的问题,提出基于RBF神经网络的MVDR算法,采用RBF神经网络快速逼近MVDR算法权矢量,代替原先MVDR算法中的矩阵求逆过程,再将RBF神经网络逼近后的MVDR算法权矢量用于波束形成当中,实现阵列信号处理。
仿真结果表明,改进算法能快速逼近任意波束形成算法的权矢量,减少计算量,具有良好的波束赋形效果,与传统波束形成算法相比,两者权矢量距离差非常小,信号跟踪能力也很强,并且改进算法无需知道阵列信号的统计特征,具有较强的实用性。
将改进算法应用于智能天线[10]当中,将对提高通信质量、抑制干扰信号、实时处理信息发挥作用。
[1] Shang Feng, Zhang Baojun. On Study of thefeeding method used for wide-banded micro-strip antwnna[J]. The Journal of China Universities of Posts and Telecommunications,2011,18(S):158-160.
[2] 崔大鹏,行小帅,李竹,等. 基于LMS 算法的自适应滤波方法研究[J]. 计算机应用与软件,2011,28(3):128-130.
[3] Yu Lei, Wei Liu, Langley R. SINR Analysisof the Subtraction-Based SMI Beamformer[J].IEEE Signal Processing Society,2010,58(11):5926-5932.
[4] Moonnen M, Proudler I K. MVDR beamforming and generalized sidelobe cancellation based on inverse updating with residual extraction[J]. IEEE Circuits and Systems Society, 2010,47(4):352-358.
[5] 邢广成,强天伟.人工神经网络的发展与应用[J]. 科技风,2012,30(15):65-66.
[6] 王永良,丁前军,李荣峰. 自适应阵列处理[M]. 北京:清华大学出版社,2009:18-19.
[7] 刘金琨. RBF神经网络自适应控制MATLAB仿真[M].北京:清华大学出版社,2014:20-25.
[8] 刘云芳,周围,连宇杭. 基于神经网络的特征空间波束形成[J]. 新技术·新业务,2013,12(11):43-46.
[9] 刘聪锋. 稳健自适应波束形成算法[M]. 西安:西安电子科技大学出版社,2012:10-12.
[10] 商锋.北斗天线的研究现状及其面临的技术问题[J]. 西安邮电大学学报,2013,18(5):1-7.
[责任编辑:瑞金]
Beamforming algorithm based on RBF neural network
ZHANG Baojun, LU Mengyi, CHEN Zhiqing, CAO Yaping
(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
A beamforming algorithm based on radial basis function (RBF) neural network is presented in this paper. According to the minimum variance distortionless response (MVDR) algorithm, the weight vector is calculated by the covariance matrix of the received signal; the covariance matrix is put into RBF neural network in the form of column vector, and RBF neural network is trained in order to approximate to the weight vector of MVDR algorithm. The trained RBF neural network is then used in the beamforming. The RBF neural network can be adaptive to output the corresponding weight vector according to the received signal from different angles. Simulation results show that the new algorithm can fast-approximate to weight vectors of any beamforming algorithm. The effect is good compared with that of the existing beamforming algorithm. The new algorithm can reduce the complexity of the algorithm and reduce the amount of calculation.
beamforming algorithm, minimum variance distortionless response (MVDR) algorithm, artifical neural network(ANN), radial basis function (RBF)
2015-01-05
陕西省教育厅科学研究计划资助项目(2013JK0627)
张宝军(1972-),男,副教授,从事通信信号处理和无线定位研究。E-mail:zbj@xupt.edu.cn卢梦怡(1991-),女,硕士研究生,研究方向为电子与通信工程。E-mail:lmy330724@163.com
10.13682/j.issn.2095-6533.2015.06.008
TN911.7
A
2095-6533(2015)06-0033-04
