L-fuzzy拓扑滤子收敛空间

杨小飞， 马生全

(1.西安工程大学 理学院， 陕西 西安 710048；2.海南师范大学 信息科学技术学院， 海南 海口 571158)



·数理科学·

L-fuzzy拓扑滤子收敛空间

杨小飞1， 马生全2

(1.西安工程大学 理学院， 陕西 西安 710048；2.海南师范大学 信息科学技术学院， 海南 海口 571158)

为给出一种新的滤子收敛结构，利用逻辑和拓扑方法，得到了L-fuzzy拓扑滤子收敛结构,该结构和L-fuzzy拓扑是范畴同构的，可以利用它研究多值拓扑空间的性质。

L-fuzzy拓扑滤子收敛空间;L-fuzzy拓扑空间; 范畴同构

在拓扑学中,借助于邻域算子可以得到与拓扑结构同构的拓扑滤子收敛结构[1-2],用这种滤子收敛描述一些拓扑性质是很直观和方便的。在多值拓扑空间中,由于采用不同的逻辑系统和不同的模糊视角,多值滤子收敛结构出现了许多不同的版本[3-4]。与本文较为接近的是文献[3],他们采用了L-fuzzy滤子,这种L-fuzzy滤子要么收敛于xλ要么不收敛。本文采用的是L-滤子,这种L-滤子收敛于点xλ是有程度的(具体见下文)。由此可见,在多值拓扑空间的研究中,由于人们对模糊事物认识的不同,可能会出现形式差别较大的滤子收敛结构,但幸运地,它们都和多值拓扑同构。由此也说明,多值拓扑不是拓扑的简单推广,而是一种更丰富的结构。本文中出现的L是带有逆合对应的完全分配格,未解释的其他概念参考文献[5-6]。

1 预备知识

定义1[5]1)设L是完备格,a∈L(a≠0)。若对满足a≤b∨c的任意b,c∈L都有a≤b或者a≤c,则称a是L的余素元。L的余素元的全体记为Copr(L)。对偶地,可以定义L中的素元,L的素元的全体记为Pr(L)。

2)在完备格上定义关系◁如下:对任意的a,b∈L,a◁b当且仅当对L的任意子集S,当∨S≥b时必存在s∈S使得s≥a。记β(a)={b∈L|b◁a}。对偶地可定义▷,记α(a)={b∈L|b▷a}。

定义2[7]1)设L是完备格,X是一个集合。则称满足下面条件的映射τ:LX→L为X上的一个L-fuzzy拓扑:

(LFT1)τ(0x)=τ(1X)=1。

(LFT2)τ(A1)∧τ(A2)≤τ(A1∧A2)(∀A1,A2∈LX)。

称偶对(X,τ)是L-fuzzy拓扑空间。

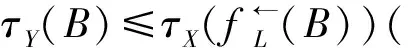
定义3[8]1)L-fuzzy邻域算子是一族满足下列条件的映射(这时称序对(X,N )是L-fuzzy邻域空间)N={Nxλ:LX→L|xλ∈Copr(LX)}(A,B∈LX,xλ,yγ∈Copr(LX)):

(LN1)Nxλ(1X)=1,Nxλ(0X)=0。

(LN2)若xAA,则Nxλ(A)=0。

(LN3)Nxλ(A∧B)=Nxλ(A)∧Nxλ(B)。

若N还满足

则称N是L-fuzzy拓扑邻域算子，且称序对(X,N )是L-fuzzy拓扑邻域空间。

2)设(X,NX)和(Y,NY)是两个L-fuzzy邻域空间，则称满足下列条件的映射f:X→Y是一个连续映射(∀A∈LY,∀xλ∈Copr(LX)):

容易验证L-fuzzy邻域空间(特别地，L-fuzzy拓扑邻域空间)及其连续映射构成一个范畴，称这个范畴为L-fuzzy邻域空间范畴(特别地，L-fuzzy拓扑邻域空间范畴)，记作LFN(特别地，LFTN)。

定义4[9](1)设L，M是完备格，则称满足下列条件的映射F:LX→M是X上的(L,M)-fuzzy滤子(L=M时称F为L-fuzzy滤子，M=2时称F为L-滤子)：

(LMFil1)F (1X)=1,F (0X)=0。

(LMFil2)若A≤B,则F (A)≤F (B)。

(LMFil3)F (A)∧F (B)=F (A∧B)。

L-滤子的全体记为F(X,L)。

定义5 1)设X是个集合，则称满足下列条件的映射Conv:F(X,L)→LJ(LX)为L-fuzzy主滤子收敛结构(这时称(X,Conv)为L-fuzzy主滤子收敛空间)：

(LConvF1)Conv[xλ](xλ)=1(∀xλ∈J(LX)),这里[xλ]={A∈LX|xλ≤A}。

(LConvF2)若F ⊆G，则ConvF≤ConvG。

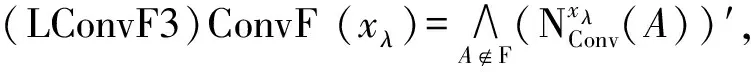
2)称满足下列条件的L-fuzzy主滤子收敛结构Conv为L-fuzzy拓扑滤子收敛结构(这时称(X,Conv)为L-fuzzy拓扑滤子收敛空间)：

3)设(X,ConvX)和(Y,ConvY)是L-fuzzy主滤子收敛空间，则称满足下列条件的映射f:X→Y是一个连续映射(∀F∈F(X,L),∀xλ∈J(LX))：

L-fuzzy主滤子收敛空间(特别地，L-fuzzy拓扑滤子收敛空间)及连续映射构成一个范畴，记为LPFConv(特别地,LTFConv)。

注1 1)称(X,Conv)为L-fuzzy主滤子收敛空间的缘由之一是条件(LConvF3)可以推出

2)由(LConvF4)和(LConvF3)可知当xλ≤xμ时ConvF(xλ)≤ConvF(xμ)(这说明在这样的L-fuzzy拓扑滤子收敛空间中有层次结构)。

2 主要结果

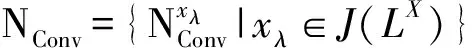
(LN2)若xλA,则A∉[xλ]。因此

由(LConvF4)知(LN4)成立。

设(X,N )是L-fuzzy拓扑邻域空间，xλ∈J(LX)。定义如下映射ConvN:F(X,L)→LJ(LX)

则下面命题成立。

命题2 ConvN是L-fuzzy拓扑滤子收敛结构。

证 明 (LConvF1)对任意的A∉[xλ]，有xλA,从而由(LN2)知Nxλ(A)=0。因此ConvN[xλ] (xλ)=1。

任取α∈α(Nxλ(A))∩Pr(L),令

Fα={C∈LX|Nxλ(C)α}。

下面证明Fα是L-滤子。(LFil1)因为Nxλ(1X)=1α和Nxλ(0X)=0≤α,所以1X∈Fα和0X∉Fα。(LFil2)设B∈Fα且B≤C，则Nxλ(B)≤Nxλ(C)。又因为Nxλ(B)α,所以Nxλ(C)α，这说明C∈Fα。(LFil3)设B,C∈Fα,则Nxλ(B∧C)=Nxλ(B)∧Nxλ(C)α,从而B∧C∈Fα。否则，由α是素元可知Nxλ(B)≤α或者Nxλ(C)≤α,这与条件B，C∈Fα矛盾。显然有A∉Fα,从而Fα∈I。对任意的都有f(Fα)∉Fα，从而可得Nxλ(f(Fα))≤α。因此由L是完全分配格和α的任意性知由f的任意性知

命题3 设(X,N )是L-fuzzy拓扑邻域空间，则NConvN=N。

证 明 由命题2中的(LConvF3)的证明可得。

命题4 设(X,Conv)是L-fuzzy拓扑滤子收敛空间，则ConvNConv=Conv。

证 明 对任意的F∈F(X,L)及xλ∈J(LX)，由命题2及定义5中的条件(LConvF3)知

反之，令I={A∈LX|A∉F},JA={G∈F (X,L)|A∉G }。因为L是完全分配格，所以

命题5 若f:(X,NX)→(Y,NY)是连续的，则f:(X,ConvNX)→(Y,ConvNY)也是连续的。

命题6 若f:(X,ConvX)→(Y,ConvNY)是连续的，则f:(X,NConvX)→(Y,NConvY)也是连续的。

这说明f:(X,NConvX)→(Y,NConvY)是连续的。

由命题1～6知LTFConv与LFTN范畴同构,另外,在文献[8]中证明了LFTN与LFTop范畴同构。所以下面定理成立。

定理1 LTFConv与LFTop范畴同构。

从上面证明过程也可以看到,这个同构函子可以扩张到更大的范围。

定理2 LPFConv与LFN范畴同构。

[1] PREUSS G. Foundation of Topology[M]. London: Kluwer Academic Publishers, 2002.

[2] 杨小飞,李生刚.用预邻域系算子、预开邻域基算子和预基确定预拓扑[J].西北大学学报(自然科学版),2008, 38(3): 349-353.

[3] PANG B, FANG J M.L-fuzzy Q-convergence structures[J].Fuzzy Sets and Sestems, 2011, 182: 53-65.

[4] YAO W. Moore-Smith convergence in (L,M)-fuzzy topology[J].Fuzzy Sets and Sestems, 2012, 190: 47-62.

[5] LIU Y M, LUO M K. Fuzzy Topology[M].Singapore: World Scientific Publishing, 1997.

[6] 王国俊. 拓扑分子格理论[M].西安:陕西师范大学出版社, 1990.

[7] KUBIAK T. On fuzzy topologies[D].Poland: Adam Mickiewicz University, 1985.

[8] SHI F G.L-fuzzy interiors andL-fuzzy closures[J].Fuzzy Sets and Systems, 2009, 160: 1218-1232.

(编 辑亢小玉)

L-fuzzy topological filter convergence spaces

YANG Xiao-fei1, MA Sheng-quan2

(1.College of Science, Xi′an Polytechnic University, Xi′an 710048, China; 2.College of Information Science and Technology, Hainan Normal University, Haikou 571158， China)

To give a new fuzzy filter convergence structure.Using methods of logical and topological theory.It is proved thatL-fuzzy topological filter convergence spaces are categorically isomorphic toL-fuzzy topological spaces.In this case, some properties in many-valued topological space can be studied by convergence ofL-filters.

L-fuzzy topological filter convergence spaces;L-fuzzy topological spaces; categorical isomorphism

2014-01-18

国家自然科学基金资助项目(11271297)；陕西省教育厅基金资助项目(2013JK0568；2013JK0591)；西安工程大学博士科研启动费基金资助项目(BS1319)

杨小飞,男,河南洛阳人,博士,从事格上拓扑学研究。

O157.5

：ADOI：10.16152/j.cnki.xdxbzr.2015-03-004