一类新图的伴随多项式的分解及其补图的色等价性

2015-02-27张秉儒

西北大学学报（自然科学版） 2015年3期

关键词：图论子图归纳法

宝音，张秉儒

(1.青海民族大学蒙学系，青海西宁 810007；2.青海师范大学数学系，青海西宁 810008)

·数理科学·

一类新图的伴随多项式的分解及其补图的色等价性

宝音1，张秉儒2

(1.青海民族大学蒙学系，青海西宁 810007；2.青海师范大学数学系，青海西宁 810008)

伴随多项式;因式分解;色等价性

1 预备知识

代数图论是从图的组合结构出发研究其代数性质,用代数指标反映图的组合构信息人们试图研究其图多项式逆问题,即利用图多项式本身所蕴涵的图论组合意义,刻画色多项式所确定的图和一些图的色等价类,用伴随多项式理论研究色唯一图和色等价图,找到了许多色唯一图和刻画了许多色等价图,最新成果包含在Koh，Dong和Teo完成的专著《Chromaticity and Chromatic Polynomials of Graphs 》中。本文的主要目的是运用图的伴随多项式的性质,讨论图的伴随多项式的因式分解的图论方法，以研究一个图的补图的色等价图的新方法。

设p(G,λ)为图G的色多项式,称图G与H色等价,若P(G,λ)=P(H,λ);称图G是色唯一图,若从P(H,λ)=P(G,λ)得到图H与G同构,记为G≅H.Chao和Whitehead于1978年首先提出色等价图和色唯一图的概念[3-4]。1987年刘儒英提出了图G的伴随多项式h(G,x)和伴随唯一性的概念[5],并在色唯一图的研究中获得一系列新成果[6-8]。目前色等价图的结构规律尚待解决。

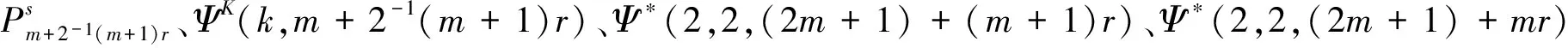
2 图的伴随多项式的概念

设G是p的阶图, 若图G的生成子图G0的所有分支是完全图,则称G0为G图的理想子图。用bi(G)表示图G的具有p-i个分支的理想子图的个数(0≤i≤p-1),由文献[4]的定理15，可知

(1)

这里是p=|V(G)|,(λ)k=λ(λ-1)(λ-2)…(λ-k+1)。

定义1[5]设G是p阶图,则图G的多项式

(2)

称为简单图G的伴随多项式,h(G,x)可以简记为h(G)。

图G的每个分支或是K1或是K2的生成子图称为图G的一个匹配,图G的一个k-匹配就是含有k条边的匹配,由G的理想子图的个数bi(G)的定义即得如下的引理。

引理1[5]若G是无三角形K3的图,则bi(G)等于图G的i-匹配的数目。

定义2 称图G与H是伴随等价的,若h(G,x)=h(H,x);称图G是伴随唯一的,若从h(H,x)=h(G,x)推出图G与H同构,记为H≌G。

我们常用到图的伴随多项式h(G,x)的如下的基本性质。

引理3[7]设uv∈E(G)且uv不属于图G的任何三角形,则有

h(G,x)=h(G-uv,x)+xh(G-{u,v},x)。

引理4[7]设图G具有k个分支G1,G2,…,Gk,则有

设G是任意的连通图,其伴随多项式h(G,x)以下简记为h(G)。不再赘述。

根据引理4，容易推知如下的引理。

引理5 设G和H是任意的两个图,K1是一个孤立点,n≥2是任意的自然数,则有

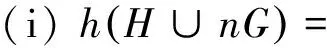
h(H)h(nG)=h(H)hn(G);

h(H)h(nK1)=xnh(H)。

引理6[10]设n≥2是自然数,Sn+1表示具有n个顶点的星图,则有

(i)h(Sn+1)=xh(Sn)+xn;

(ii)h(Sn+1)=xn+1+nxn。

引理7[11]设m,k∈N,k≥m≥2,则有h(Ψ(k,m))=xk[h(Pm)+kh(Pm-1)]。

3 几类新图的伴随多项式

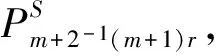
图1 图ΨK(k,m+2-1(m+1)r),m=2t+1Fig.1 ΨK(k,m+2-1(m+1)r),m=2t+1

图2 图Ψ*(2,2,m+2-1(m+1)r),m=2t+1Fig.2 Ψ*(2,2,m+2-1(m+1)r),m=2t+1

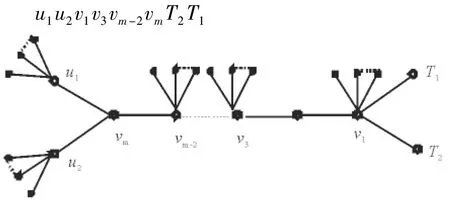
图3 图ΨT(r,2,m+2-1mr),m=2tFig.3 ΨT(r,2,m+2-1mr),m=2t

引理8 设k≥1是任意的自然数,m是奇数,m≥r≥3,则有

(i)h(ΨK(1,m+2-1(m+1)r))=

xrh(ΨK(1,(m-2)+2-1(m-1)r))]，

(3)

(ii)h(ΨK(2,m+2-1(m+1)r))=

2xrh(ΨK(1,(m-2)+2-1(m-1)r))]，

(4)

(iii)h(ΨK(k,m+2-1(m+1)r))=

kxrh(ΨK(1,(m-2)+2-1(m-1)r))]。

(5)

证明如图1所示,在图ΨK(1,m+2-1(m+1)r)和ΨK(2,m+2-1(m+1)r)中均取边e=u1v1,则由引理3和引理4,依次得到以下两个公式

h(ΨK(1,m+2-1(m+1)r))=

xr+1h(ΨK(1,(m-2)+2-1(m-1)r))，

h(ΨK(2,m+2-1(m+1)r))=

xh(ΨK(2,m+2-1(m+1)r))+

xr+2h(ΨK(1,(m-2)+2-1(m-1)r))。

由上面的两式立即得到式(3)和(4)。

如图1所示,在图ΨK(k,m+2-1(m+1)r)中取边e=u1v1,由引理3和引理4,即得

h(ΨK(k,m+2-1(m+1)r))=

xh(ΨK(k-1,m+2-1(m+1)r))+

xr+kh(ΨK(1,(m-2)+2-1(m-1)r))。

(6)

下证式(5)成立,对顶点数k作数学归纳法,当k=1,2时,由式(3)和(4)可知,此时公式成立;假定公式对k-1(k≥3)的情形成立,即

h(ΨK(k-1,m+2-1(m+1)r))=

(k-1)xrh(ΨK(1,(m-2)+

2-1(m-1)r))]，

则对于k的情形,根据式(6)及归纳假定，有

h(ΨK(k,m+2-1(m+1)r))=

xh(ΨK(k-1,m+2-1(m+1)r))+

xr+kh(ΨK(1,(m-2)+

2-1(m-1)r))=

(k-1)xrh(ΨK(1,(m-2)+

2-1(m-1)r))]+

xr+kh(ΨK(1,(m-2)+2-1(m-1)r))=

kxrh(ΨK(1,(m-2)+2-1(m-1)r))]，

即当k时公式也成立,由数学归纳法原理可知,对任意的自然数k,式(5)成立。

引理9 设m为奇数,r是自然数,m>r≥3,则有

(i)h(Ψ*(1,2,m+2-1(m+1)r))=

x[h(ΨK(2,m+2-1(m+1)r))+

xrh(Ψ*(1,2,(m-2)+2-1(m-1)r))]，

(7)

(ii)h(Ψ*(2,2,m+2-1(m+1)r))=

x2[h(ΨK(2,m+2-1(m+1)r))+

2xrh(Ψ*(1,2,(m-2)+2-1(m-1)r))]。

(8)

证明 (i) 如图2所示,m为奇数,此时删除1度点T1,T2,U1,U2以外,其余的顶点数为m+2-1(m+1)r,在图Ψ*(1,2,m+2-1(m+1)r)中取边e=T1Vm,由引理3和引理4,得到

h(Ψ*(1,2,m+2-1(m+1)r)) =

xh(ΨK(2,m+2-1(m+1)r))+

xr+1h(Ψ*(1,2,(m-2)+2-1(m-1)r))，

由此可知式(7)成立;

(ii) 在图Ψ*(2,2,m+2-1(m+1)r)中取边e=T1Vm,同理可得

h(Ψ*(2,2,m+2-1(m+1)r))=

xh(Ψ*(1,2,m+2-1(m+1)r))+

xr+2h(Ψ*(1,2,(m-2)+2-1(m-1)r))，

由此及式(7)可推知式(8)成立。

引理10 设m为偶数,r是自然数,m>r≥3,则有

h(ΨK(2,(m+1)+2-1(m+2)r))=

h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))+

xr+1h(ΨK(2,(m-1)+2-1mr))。

(9)

证明参考图1,m是偶数,则m+1是奇数,故d(vm)=2,d(vm+1)=r+1,在图ΨK(2,(m+1)+2-1(m+2)r)中取边e=vmvm+1,则由引理3和引理4,即得式(9)。

引理11 设m为偶数时,r∈N,m≥r≥3,则有

(i)h(ΨT(r,2,m+2-1mr))=

h(ΨK(2,(m+1)+2-1(m+2)r))=

h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))+

xr+1h(ΨK(2,(m-1)+2-1mr))，

(10)

(ii)h(ΨT(2r,2,m+2-1mr))=

h(Sr+1)[h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))+

2xr+1h(ΨK(2,(m-1)+2-1mr))]。

(11)

证明 (i) 当m为偶数时,如图3所示,图ΨT(r,2,m+2-1(m+1)r)即为ΨK(2,(m+1)+2-1(m+2)r),故由式(9)即得式(10);

(ii)当m为偶数时,此时m-1为偶数,d(u1)=r+1,d(Vm)=3,如图3所示,在图ΨΤ(2r,2,m+2-1mr)中取e=u1Vm,由引理3和引理4,并运用式(10),即得

h(ΨT(2r,2,m+2-1(m+1)r))=

h(Sr+1)h(ΨT(r,2,m+2-1mr))+

xr+1h(Sr+1)h(ΨK(2,(m-1)+2-1mr))=

h(Sr+1)[h(ΨT(r,2,m+2-1mr))+

xr+1h(ΨK(2,(m-1)+2-1mr))]=

h(Sr+1)[h(Sr+1)h(ΨK(1,(m-1)+

2-1mr))+xr+1h(ΨK(2,(m-1)+2-1mr))+

xr+1h(ΨK(2,(m-1)+2-1mr))]=

h(Sr+1)[h(Sr+1)h(Ψ*(1,2,(m-1)+

2-1mr))+2xr+1h(ΨK(2,(m-1)+

2-1mr))]。

由此可知式(11)成立。

4 两类图的伴随多项式的因式分解

4.1 两类图的伴随多项式

图4 图Ψ*(2,2,(2m+1)+(m+1)r),m=2t+1Fig.4 Ψ*(2,2,(2m+1)+(m+1)r),m=2t+1

图5 图Ψ*(2,2,(2m+1)+mr), m=2tFig.5 Ψ*(2,2,(2m+1)+mr), m=2t

引理12 设m,r是自然数,m>r≥3,则有

(i) 若m为奇数,

h(Ψ*(2,2,(2m+1)+(m+1)r))=

h(ΨK(2,m+2-1(m+1)r))

[xh(ΨK(2,m+2-1(m+1)r))+

2xr+1h(Ψ*(1,2,(m-2)+2-1(m-1)r))]

(12)

(ii) 若m为偶数,

h(Ψ*(2,2,(2m+1)+mr))=

h(Ψ*(1,2,(m-1)+2-1mr))

[h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))+

2xr+1h(ΨK(2,(m-1)+2-1mr))]

(13)

证明 (i) 如图4所示,因为m是奇数,故d(Vm)=r+2,d(Vm+1)=2,在图Ψ*(2,2,(2m+1)+(m+1)r)中取边e=VmVm+1,则由引理3、引理4，有

h(Ψ*(2,2,(2m+1)+(m+1)r))=

h(ΨK(2,m+2-1(m+1)r))

h(Ψ*(1,2,m+2-1(m+1)r))+

xr+1h(Ψ*(1,2,(m-2)+

2-1(m-1)r))h(ΨK(2,m+2-1(m+1)r))=

h(ΨK(2,m+2-1(m+1)r))

[h(Ψ*(1,2,m+2-1(m+1)r))+

xr+1h(Ψ*(1,2,(m-2)+2-1(m-1)r))]，

把式(7)代入上式,即得

h(Ψ*(2,2,(2m+1)+(m+1)r))=

h(ΨK(k,m+2-1(m+1)r))

[xh(ΨK(2,m+2-1(m+1)r))+

2xr+1h(Ψ*(1,2,(m-2)+2-1(m-1)r))]，

由此可知式(12)成立;

(ii) 如图5所示,因为m是偶数,故d(Vm)=2,d(Vm+1)=r+2,在图Ψ*(2,2,(2m+1)+mr)中取边e=VmVm+1,则由引理3和引理4,有

h(Ψ*(2,2,(2m+1)+mr))=

h(Ψ*(1,2,(m-1)+

2-1mr))h(ΨK(2,(m+1)+

2-1(m+2)r))+

xr+1h(ΨK(2,(m-1)+

2-1mr))h(Ψ*(1,2,(m-1)+2-1mr))=

h(Ψ*(1,2,(m-1)+2-1mr))·

[h(ΨK(2,(m+1)+2-1(m+2)r))+

xr+1h(ΨK(2,(m-1)+2-1mr))]，

把式(9)代入上式,即得

h(Ψ*(2,2,(2m+1)+mr))=

h(Ψ*(1,2,(m-1)+

2-1mr))[h(Sr+1)h(Ψ*(1,2,(m-1)+

2-1mr))+

2xr+1h(ΨK(2,(m-1)+2-1mr))]，

因此式(13)成立。

4.2 因式分解定理

定理1 设m是奇数,r是自然数,m>r≥3,则有

(i)h(Ψ*(2,2,(2m+1)+

(m+1)r)∪K1)=

h(ΨK(2,m+2-1(m+1)r))·

h(Ψ*(2,2,m+2-1(m+1)r))，

(14)

(ii)h(Ψ*(2,2,(2m+1)+

(m+1)r)∪K1)=

h(ΨK(2,m+2-1(m+1)r)

∪Ψ*(2,2,m+2-1(m+1)r))。

(15)

证明

(i) 若m是奇数, 由引理5,并根据(12)和(8)两式,即得

h(Ψ*(2,2,(2m+1)+(m+1)r)∪K1)=

xh(Ψ*(2,2,(2m+1)+(m+1)r))=

xh(ΨK(2,m+2-1(m+1)r))·

[xh(ΨK(2,m+2-1(m+1)r))+

2xr+1h(Ψ*(1,2,(m-2)+

2-1(m-1)r))]=

h(ΨK(2,m+2-1(m+1)r))·

x2[h(ΨK(2,m+2-1(m+1)r))+

2xrh(Ψ*(1,2,(m-2)+

2-1(m-1)r))]=

h(ΨK(2,m+2-1(m+1)r))

h(Ψ*(2,2,m+2-1(m+1)r))

所以式(14)成立;

(ii) 根据式(14)及引理4,容易推知式(15)成立。

定理2 设m是偶数,r是自然数,m>r≥3,则有

(i)h(Ψ*(2,2,(2m+1)+

mr)∪Sr+1)=

h(Ψ*(1,2,(m-1)+

2-1mr))h(ΨT(2r,2,m+2-1mr))

(16)

(ii)h(Ψ*(2,2,(2m+1)+mr)∪Sr+1)=

h(Ψ*(1,2,(m-1)+2-1mr)∪

ΨT(2r,2,m+2=1mr))

(17)

证明 (i) 若m是偶数,由引理5,并根据(13)和(11)两式,即得

h(Ψ*(2,2,(2m+1)+mr)∪Sr+1)=

h(Sr+1)h(Ψ*(2,2,(2m+1)+mr))=

h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))·

[h(Sr+1)h(Ψ*(1,2,(m-1)+2-1mr))+

2xr+1h(ΨK(2,(m-1)+2-1mr))]=

h(ΨK(1,k,(m-1)+2-1mr))·

h(ΨT(2r,k,m+2-1mr))

所以式(16)也成立。

(ii) 根据引理4及式(16)可知,(17)也成立,由此可知(16)与(17)两式是等价的。

若m是形如m=2nq-1的奇数,令λn=(2nq-1)+2n-1qr,∀n∈N,则有

(2m+1)+(m+1)r=

(2n+1q-1)+2nqr=λn+1，

于是由式(14),即得以下推论。

推论1 设m=2nq-1,q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则有

h(Ψ*(2,2,λn+1)∪K1)=

h(Ψ*(2,2,λn))h(ΨK(2,λn))

(18)

在式(18)中令n=1,2,3，有如下的推论。

推论2 设m=2nq-1,q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则有

(i)h(Ψ*(2,2,λ2)∪K1)=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))，

(19)

(ii)h(Ψ*(2,2,λ3)∪K1)=

h(Ψ*(2,2,λ2))h(ΨK(2,λ2))，

(20)

(iii)h(Ψ*(2,2,λ4)∪K1)=

h(Ψ*(2,2,λ3))h(ΨΚ(2,λ3))。

(21)

推论3 设m=2nq-1,q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则有

(i)h(Ψ*(2,2,λ3)∪2K1)=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))·

h(ΨK(2,λ2))，

(22)

(ii)h(Ψ*(2,2,λ4)∪3K1)=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))h(ΨK(2,λ2))·

h(ΨK(2,λ3)) 。

(23)

证明 (i) 由引理5,并根据(20)和(19)两式,即得

h(Ψ*(2,2,λ3)∪2K1)=

xh(Ψ*(2,2,λ3)∪K1)=

xh(Ψ*(2,2,λ2))h(ΨK(2,λ2))=

h(Ψ*(2,2,λ2)∪K1)h(ΨK(2,λ2))=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))h(ΨK(2,λ2))，故式(22)成立;

(ii) 由引理5,并根据(21)和(22)两式,即得

h(Ψ*(2,2,λ4)∪3K1)=

x2h(Ψ*(2,2,λ4)∪K1)=

x2h(Ψ*(2,2,λ3))h(ΨK(2,λ3))=

h(Ψ*(2,2,λ3)∪2K1)h(ΨK(2,λ3))=

h(Ψ*(2,2,λ1))·

h(ΨK(2,λ1))h(ΨK(2,λ2))h(ΨK(2,λ3))，

故式(23)也成立。

定理3 设m=2nq-1,q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则有

(i)h(Ψ*(2,2,λn+1)∪nK1)=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))h(ΨK(2,λ2))…

h(ΨK(2,λn-1))h(ΨK(2,λn))，

(24)

(ii)h(Ψ*(2,2,λn+1)∪nK1)=

h(Ψ*(2,2,λ1)∪ΨK(2,λ1)∪ΨK(2,λ2)∪…

∪ΨK(2,λn-1)∪ΨK(2,λn))。

(25)

证明 (i) 对个数n≥2作数学归纳法。当n=2,3,4时,由(19)、(22)和(23)三式可知结论成立;假定结论对于n-1的情形成立,则对于n的情形,由引理5,并根据(18)和归纳假定,有

h(Ψ*(2,2,λn+1)∪nK1)=

xn-1h(Ψ*(2,2,λn+1)∪K1)=

xn-1h(Ψ*(2,2,λn))h(ΨK(2,λn))=

h(Ψ*(2,2,λn)∪(n-1)K1)h(ΨK(2,λn))=

h(Ψ*(2,2,λ1))h(ΨK(2,λ1))·

h(ΨK(2,λ2))…h(ΨK(2,λn-1))h(ΨK(2,λn))

即当n时结论也成立,根据数学归纳法原理可知,对于任意的自然数n≥2,结论都成立。

(ii) 根据式(24)及引理4,容易推知式(25)成立。

5 图的色价性分析

在给出几类图的伴随分解的基础上,来讨论这些图色等价性。

定理4 设m是奇数,r是自然数,m>r≥3,则图簇Ψ*(2,2,(2m+1)+(m+1)r)与ΨK(2,m+2-1(m+1)r)∪Ψ*(2,2,m+2-1(m+1)r) 二者的补图是色等价的。

证明根据式(15)知

h(Ψ*(2,2,(2m+1)+

(m+1)r)∪K1)=

h(ΨK(2,m+2-1(m+1)r)∪

Ψ*(2,2,m+2-1(m+1)r))

由此及定义2可知,图簇ΨK(2,m+2-1(m+1)r)∪Ψ*(2,2,m+2-1(m+1)r) 与Ψ*(2,2,(2m+1)+(m+1)r)二者是伴随等价的,由此及引理2,它们的补图是色等价的。

定理5 设m是偶数,r是自然数,m>r≥3,则图簇Ψ*(k,k,(2m+1)+mr)∪Sr+1与Ψ*(1,2,(m-1)+2-1mr)∪ΨT(2r,2,m+2-1mr) 二者的补图是色等价的。

证明根据式(17)知

h(Ψ*(2,2,(2m+1)+mr)∪Sr+1)=

h(Ψ*(1,2,(m-1)+2-1mr)∪

ΨT(2r,2,m+2-1mr))

由此及定义2可知,图簇Ψ*(1,2,(m-1)+2-1mr)∪ΨT(2r,2,m+2-1mr) 与Ψ*(k,k,(2m+1)+mr)∪Sr+1二者是伴随等价的,由此及引理2,它们的补图是色等价的。

由式(18)得到

h(Ψ*(2,2,λn+1)∪K1)=

h(Ψ*(2,2,λn)∪ΨK(2,λn))。

(26)

仿照定理4及定理5的证明,由式(26)和式(25),即可证明如下定理。

定理6 设∀n∈N,n≥2,且q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则两个图簇Ψ*(2,2,λn+1)∪K1与Ψ*(2,2,λn)∪ΨK(2,λn)的补图是色等价图。

定理7 设∀n∈N,n≥2,且q是奇数,q≥r≥3,λn=(2nq-1)+2n-1qr,则图簇Ψ*(2,2,λn+1)∪nK1与Ψ*(2,2,λ1)∪ΨK(2,λ1)∪ΨK(2,λ2)∪…∪ΨK(2,λn-1)∪ΨK(2,λn)的补图是色等价图。

[1]BODYJA,MURTYUSR.GraphTheorywithApplications[M].Amsterdam:North-Holland, 1976.

[2]BOLLOBASB.ModernGraphTheory[M].NewYork:Spinger-Verlag，1998.

[3]CHAOCY,WHITEHEADEG.Onchromaticequivalenceofgraph[J].SpringerLectureNoteinMathematics,1978，642：121-131.

[4]KOHKM,TEOKL.Thesearchforchromaticallyuniquegraphs[J].GraphCombin，1990(6):259-285.

[5]BIGGSN.AlgebraicGraphTheory[M].Cambridge:CambridgeUniversityPress, 1974.

[8]ZHAOHX,LIXL,LIURY.Onproblemsandconjecturesonadjointlyequivalentgraphs[J].DiscreteMathematics, 2005,295:203-212.

[9] 刘儒英.关于两类图的色多项式[J]. 科学通报, 1987(3):236.

[10] 张秉儒. 图的伴随多项式的两个因式分解定理及其应用[J]. 数学研究与评论, 2003,23(2):355-361.

[11] 郭玉琳,张秉儒.若干图簇的伴随多项式的因式分解及色性分析[J].数学的实践与认识, 2005, 35(9):167-172.

(编辑亢小玉)

The factorizations of adjoint polynomials of a kind of graphs and chromatically equivaleness of their complements

BAO Yin1， ZHANG Bing-ru2

(1.Department of Mongol, Qinghai National University, Xining 810007, China; 2.Department of Mathematics, Qinghai Normal University, Xining 810008, China)