M准则搜索节点自适应的空间调制检测算法
2015-02-27文思杰金小萍冯会真
文思杰,金小萍,冯会真
(中国计量学院 信息工程学院,浙江 杭州 310018)

M准则搜索节点自适应的空间调制检测算法
文思杰,金小萍,冯会真
(中国计量学院 信息工程学院,浙江 杭州 310018)
为了解决空间调制系统(SM)下,M算法搜索过程中搜索节点数难以确定及算法复杂度偏大的问题,提出一种搜索节点数自适应于累积度量值的检测算法(IM-ML).传统的M-ML算法在树形结构中进行搜索时每层保留的节点数为一个固定值,而我们提出的算法在每层搜索保留K个节点的前提下,保留度量值大于K个节点的有限个节点.仿真结果表明,改进后的M-ML检测算法在K值较小的情况下就能取得传统M-ML算的性能,同时降低了算法复杂度.
空间调制;M算法;M-ML算法
多输入多输出(MIMO)技术作为提高频谱利用率和系统容量的关键技术被广泛应用于无线通信系统[1].伴随着MIMO技术的发展,由于其系统结构的限制,传输信道间的干扰(ICI)与多天线发射严格的同步性(IAS)成为制约其发展的两个主要原因.
基于上述考虑,空间调制(SM,spatial modulation)[2-3]作为一种新型的MIMO发射方式被提出.SM的特点是将二维符号调制扩展到三维,新增的一维为空间维,即天线序号.系统在每一个发送时隙,只有一根发射天线处于激活状态用来发送数据,这使得空间调制系统可以有效避免信道干扰和多天线同步问题,同时空间维携带的信息可以提高频谱利用率.为了在接收端恢复出发射的信息比特,现有针对空间调制的研究工作主要集中在探寻具有高性能低复杂度的检测方法上.
面向空间调制的检测算法中最大似然检测(ML)[4]是性能最优的检测方法,但由于其采用遍历全搜索的方式使得其复杂度非常高.针对这个问题,文献[5-6]提出了以球形译码为代表的深度优先检测算法,这类算法的性能较佳,但由于算法的回溯特性造成其延时较大,且不利于硬件实现.文献[7]将宽度优先的M算法和ML算法结合起来(M-ML)引入到空间调制系统中,通过计算每层待搜索点的累积度量值来限制保留的节点,以达到减少复杂度的目的;同时因为采用并行搜索的方式使得硬件更易于实现.但是,由于该算法在每层搜索过程中保留的节点数为固定值,这个值的设定缺乏理论基础,会造成搜索过程中丢失最大似然解的概率比较大.
针对上述问题,本文根据文献[8]提出了一种基于M准则搜索节点自适应的检测算法(IM-ML).由空间调制下累积度量值概率分布的特性,将每层固定保留的K个节点进行自适应扩展,扩展参数可通过K个节点的累积度量值fK导出.IM-ML算法通过每层合理保留搜索节点在保证获得与M-ML算法相近性能的同时,降低了复杂度.
1 系统模型
考虑有Nt根发射天线Nr根接收天线的空间调制系统.数字调制方式采用MPSK,系统框图如图1.
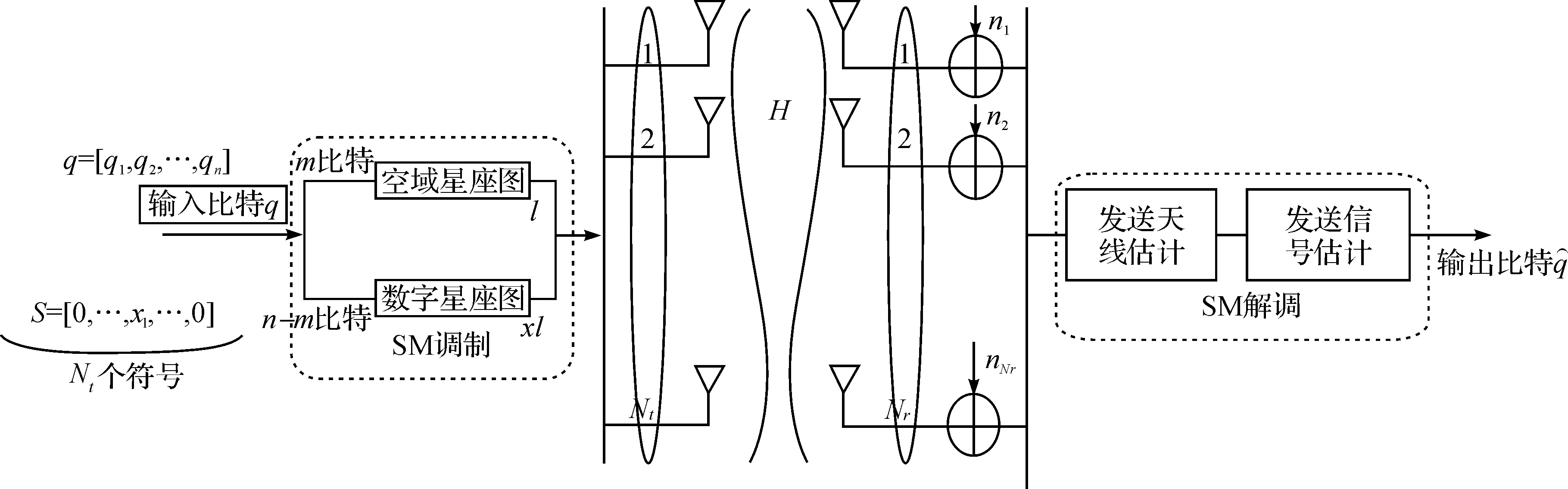
图1 空间调制系统框图Figure 1 Diagram of SM system
一连串独立随机的二进制信息比特流q=[q1q2…qm…qn]进入到SM系统的映射单元,每个调制符号包含的比特位数为log2M(M为调制阶数).前m个二进制比特映射为空域星座图中的第l根天线(l为发射天线的序号),剩余n-m个信息比特映射为星座图中的符号.S中只有被激活的天线的位置上的元素非零,即只有第l根发射天线上加载有发射符号.由此可知,总的发送信息比特由发射天线的数目和数字调制阶数决定,即空间调制技术每个时隙传输的比特数为nsm=log2M+log2Nt接收端需要检测的量有两个:1)被激活的发射天线的序号;2)发射的调制符号.估计出天线序号与调制符号后,经过发射端的映射表逆映射出原始输入比特.表1列举了3 bit·Hz-1·s-1映射规则表.
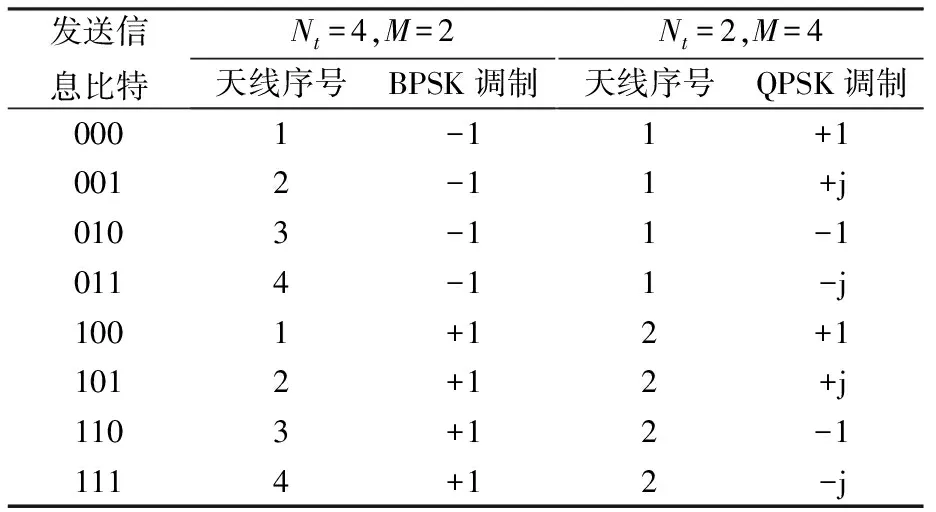
表1 3 bit·Hz-1·s-1映射规则
调制后的信号经过信道传输,在复高斯噪声n的影响下,接收天线接收到的信号可表示为
y=Hs+n.
(1)
式(1)中,y=[y1y2,…,yNr]T(T为转置符号)是Nr×1的接收向量,n=[n1,n2,…,nNr]T是均值为0、方差为σ2的加性复高斯白噪声矢量,H为Nr×Nt信道矩阵,其矩阵元素为彼此独立零均值的复高斯随机变量.对接收到信号y进行处理,完成发射信号的检测.其中性能最优的最大似然检测算法可由公式表示如下:
(2)

2 检测算法
由于最大似然检测算法复杂度很大,文献[5]提出的深度优先的低复杂度的球形译码算法,通过限制搜索半径与搜索节点来降低算法的复杂度;但是,由于该算法的回溯特性,不利于硬件实现.针对这个问题,文献[7]将宽度优先的检测算法(M算法)与ML算法结合(M-ML算法),在降低复杂度的同时,由于并行搜索的特性使其更易于硬件实现.
2.1 M-ML算法
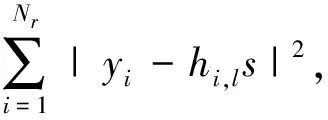
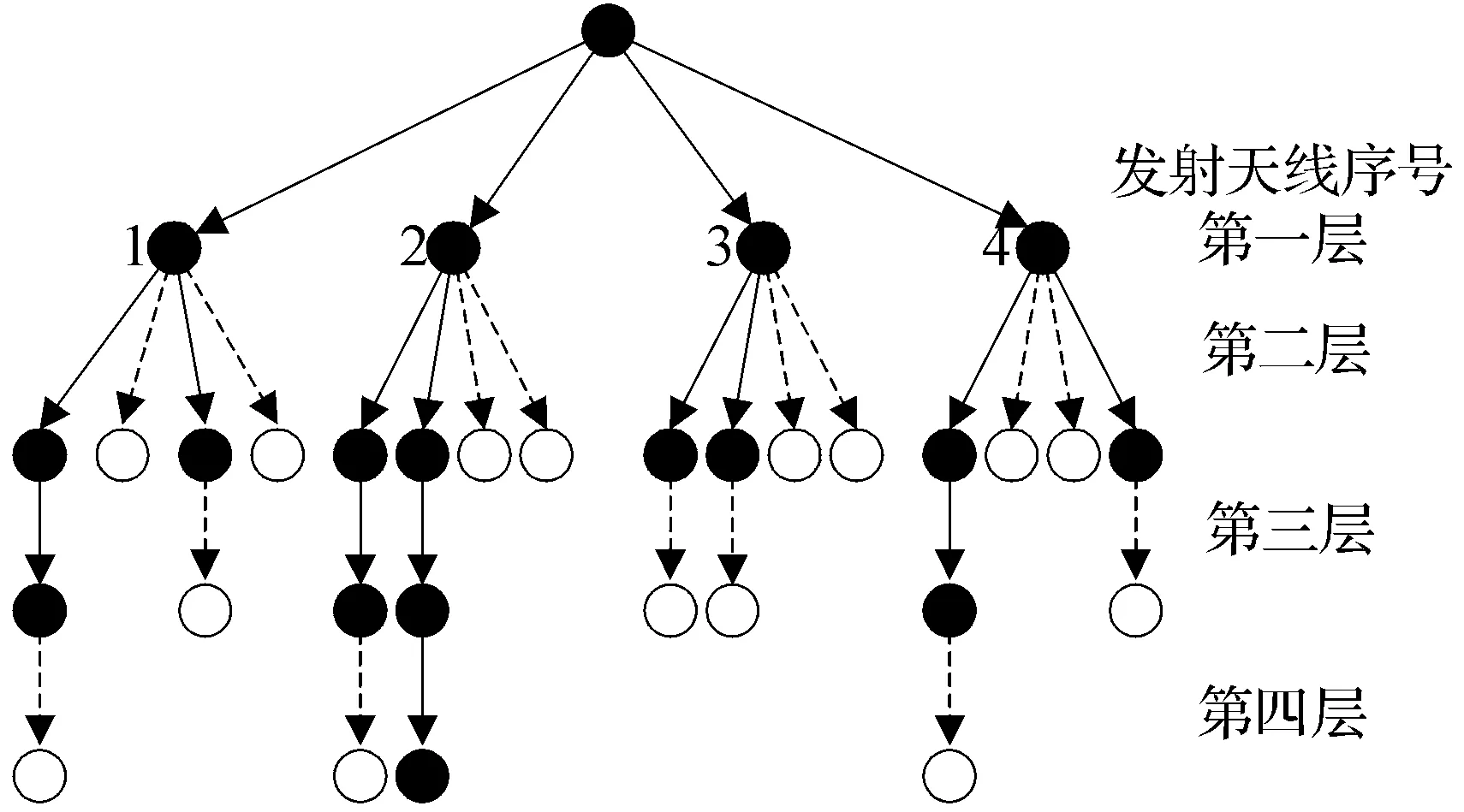
图2 M-ML算法树形结构图Figure 2 Tree structure of M-ML alogrithm
在Nt=4,Nr=4调制方式采用QPSK的SM系统下经过仿真测试,当每层保留的节点数K分别为12、6、4时可以获得逼近ML算法的性能,同时M-ML算法降低了由ML算法全搜索带来的高复杂度,并且其逐层搜索的策略便于并行操作.
2.2 IM-ML算法
由于M-ML算法在搜索时保留的节点数为经验所得,没有理论基础.在此基础上,本文提出了一种低复杂度的IM-ML算法.IM-ML算法搜索过程中在保留K个节点的累积欧氏距离fK的同时保留与K个节点度量值最接近的另外r个节点,K+r个节点的累积欧式距离记为fK+Δ,这K+r个节点将作为下一层搜索的候选节点.设ft为树形结构中第k层节点的累积度量值:
(3)
由于ni中各元素相互独立且都服从高斯分布,则ft服从自由度为Nr-k+1的卡方分布.记前K个节点的累积度量值为fK,则ft大于fK的的概率为
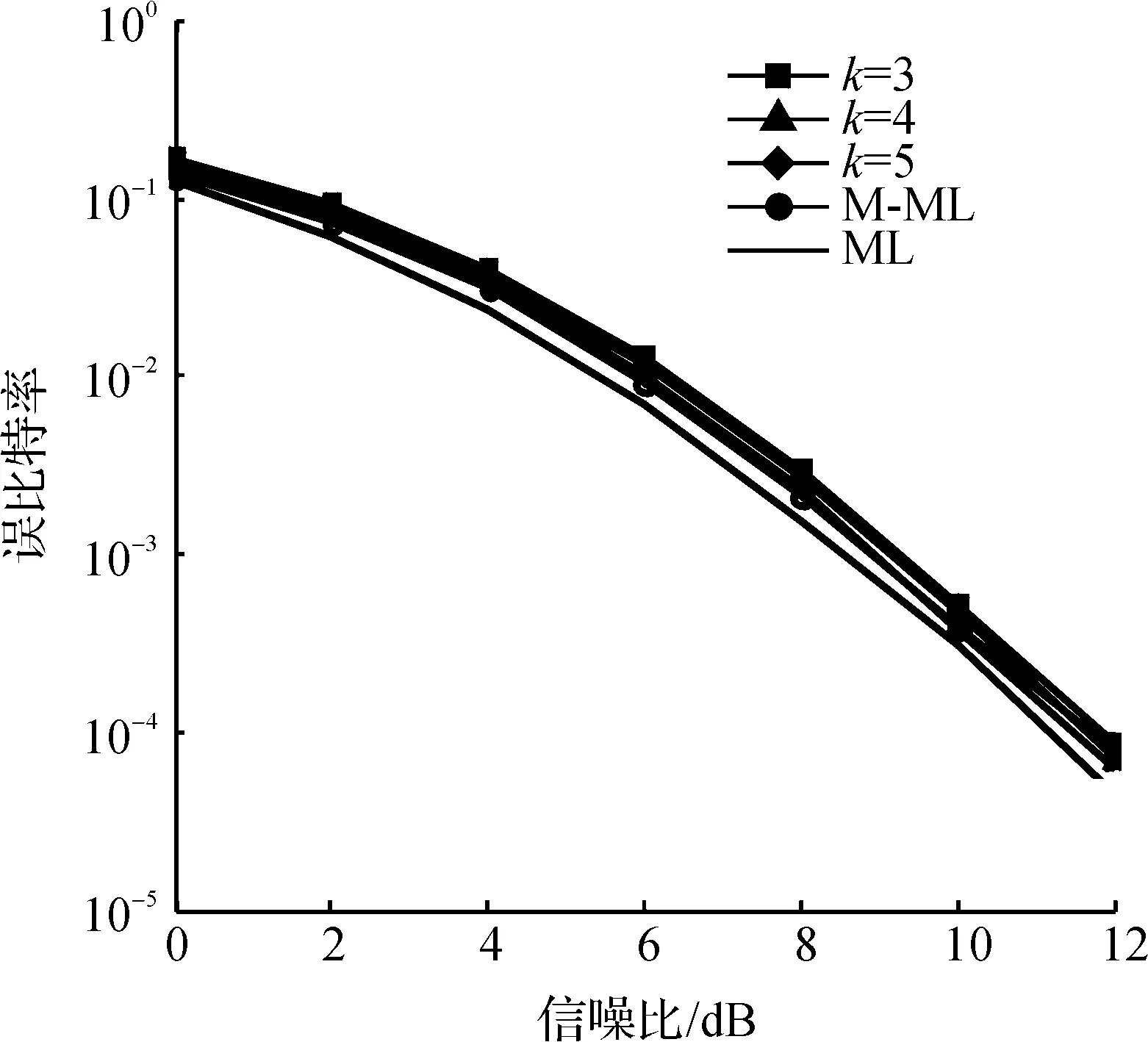
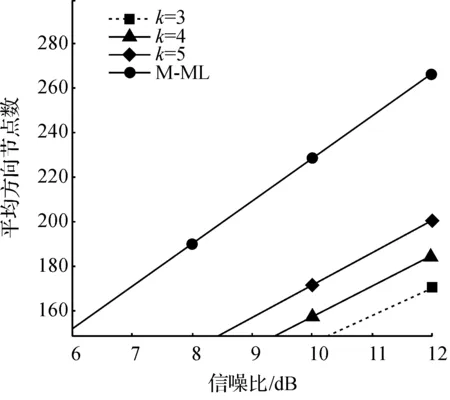
PK=Pr(ft>fK)=1-Pr(ft (4) 其中 (5) 为累积分布函数(CDF),γ(k,x)和Γ(k)分别为不完全伽马函数和伽马函数.为了减小丢失最大似然解的概率,在(3)式中引入变量Δ,使 PΔ=Pr(fk+Δ)=ηPk(0<η<1). (6) 对(6)式进行变形得到 Δ=F-1(1-ηPk;Nr-k+1)-fk. (7) 对于式(7),在信噪比(SNR)足够高的情况下得到 (8) 卡方分布的概率密度公式为 (9) 得到卡方分布的累积分布函数 (10) 对式(10)进行变形可得 (11) 令式(11)中P=1-ηPk,λ=Nr-k+1,可得到Δ的表达式如式(12). 算法流程如下: 记Q={(l,s)|l∈[1,…,Nt],s∈S}. 输入:y,H,k,λ. fori=1∶Nr 1)fl=1 for(l,s)∈Q f1(l,s)=|y1-h1,ls|2; f1(l,s)=sort|y1-h1,ls|2; fK=f1(K); 据(12)式算出Δ值; 2)if1 for(l,s)∈Qi-1 fi(l,s)=|yi-hi,ls|2+fi-1; fi(l,s)=sortfi(l,s); fK=fi(K); 据(12)式算出Δ值; (12) 仿真在SM系统下进行,采用QPSK调制,发射端与接收端的天线数各为4,同时假设信道为准静态平坦瑞利衰落信道,且在接收端已知信道状态信息.仿真结果对K=3,4,5(K初始固定保留节点数)三种不同情况下的IM-ML算法、M-ML(M=12-6-4,M为逐层保留节点数)算法和ML算法进行了误比特率的比较,同时对各算法相应的复杂度也做了比较分析.性能仿真图如图3. 图3 ML与M-ML和IM-ML算法性能比较Figure 3 BER Performance against SNR 通过仿真图可以看出随着K值越来越大,IM-ML算法的性能越好.在K=5时,IM-ML的性能与M-ML一致,在信噪比高于9 dB的区域,性能优于M-ML算法,同时在保证算法性能与空间调制系统下ML算法相比仅有0.5 dB的性能损失. 图4 M-ML算法与IM-ML不同K值复杂度Figure 4 Complexity Comparison aginst SNR 复杂度仿真图如图4,主要对比了IM-ML算法与M-ML算法访问的节点数.可以看出,IM-ML算法访问节点数明显低于M-ML算法,在信噪比为12 dB时,IM-ML比M-ML节点访问数低40%左右.经过分析可知,IM-ML算法在性能没有损失的情况下,大幅度降低了算法的复杂度,且在较高信噪比区域性能优于M-ML算法,同时复杂的降低也使得IM-ML更易于实现. 本文针对空间调制系统下,M-ML算法复杂度较高的问题提出了一种扩大搜索层节点来降低复杂度的检测算法.通过M算法与最大似然检测算法结合,利用最大似然算法的度量表达式推导出合适的Δ值来降低最大似然解丢失的概率.在保证较M-ML算法仅有0.5 dB性能损失的前提下,将算法的复杂度降低了40%. [1] MIETNRE J, SCHOBER R, LAMPLE L. Multiple-antenna techniques for wireless communication: a comprehensive literature survey[J].IEEE Commun Survey & Tutorials,2009,11(2):87-105. [2] MESLEH R, HAAS H, SINANOVIC S, et al. Spatial modulation[J].IEEE Trans on Vehicular Technol,2008,57(4):2228-2241. [3] MESLEH R, HAAS H, AHN C W, et al. Spatial modulation: a new low complexity spectral efficiency enhancing technique[C]//IEEE First International Conference on Communications and Networking in China. Beijing: IEEE,2006:1-5. [4] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Spatial modulation:optimal detection and performance analysis[J].IEEE Communication Letters,2008,12(8):545-547. [5] YOUNIS A, MESLEH R, HAAS H. Reduced complexity sphere decoder for spatial modulation detection receivers[C]//IEEE Global Telecommunication Conference. Miami: IEEE,2010:1-5. [6] YOUNIS A, RENZO M, MESLEH R, et al. Sphere decoding for spatial modulation[C]//IEEE International Conference on Communications. Kyoto: IEEE,2011:1-6 [7] ZHENG Jianhong, YANG Xiaobo, LI Zhe. Low-complexity detection method for spatial modulation based on M-algorithm[J].IEEE Electronics Letters,2014,50(21):1552-1554. [8] HAN Shuangshuang, CUI Tao, TELLAMBURA C. Improved K-Best Sphere Detection for Uncoded and Coded MIMO Systems[J].IEEE Wireless Communications Letters,2012,1(5):472-475. Adaptive searching node algorithm for spatial modulation based on M-algorithm WEN Sijie, JIN Xiaoping, FENG Huizhen (College of Information Engineering, China Jiliang University, Hangzhou 310018, China) To solve the problem of being hard to fix the node number in the search process and the high complexity of M-algorithm under spatial modulation, an improved M-ML algorithm(IM-ML) with node number searching adapted to accumulated metrics was presented. Compared with the traditional M-algorithm in which the number of retained nodes at each level of the tree structure was a fixed value, the IM-ML algorithm retained the finite number of nodes where the accumulated metrics was greater thanKnodes under the premise that theKnodes had been kept at each level of the tree structure. Simulation results showed that the IM-ML algorithm could obtain a near-optimum bit error rate performance compared with the traditional M-ML algorithm and its complexity reduced. spatial modulation; M-algorithm; M-ML algorithm 1004-1540(2015)03-0280-05 10.3969/j.issn.1004-1540.2015.03.006 2015-03-26 《中国计量学院学报》网址:zgjl.cbpt.cnki.net 文思杰(1992- ),男,湖北省荆门人,硕士研究生,主要研究方向为空间调制系统下的检测算法.E-mail:wsj973507837@163.com 通讯联系人:金小萍,女,副教授.E-mail:jxp1023@cjlu.edu.cn TN914 A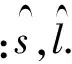
3 仿真结果及分析
4 结 语
