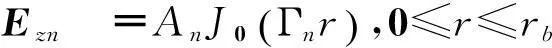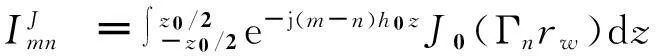Ka波段过模慢波结构色散曲线的数值求解*



Ka波段过模慢波结构色散曲线的数值求解*

武大鹏，舒挺，张华

(国防科技大学 光电科学与工程学院，湖南 长沙410073)

摘要：运用场匹配法，结合Ka波段过模慢波结构的实际情况，进行轴对称周期慢波结构色散关系的理论推导，得到了一种快速、准确计算适应Ka波段过模慢波结构的色散特性计算方法。根据推导结果，采用MATLAB程序编程计算了Ka波段过模盘荷波导的色散曲线。将计算得到的色散曲线与成熟的商业软件计算得到的结果进行了对比，两者误差在2%以内，验证了数值算法的可靠性。计算得到的色散曲线可以辅助选取Ka波段微波源的结构参数，对器件设计有一定参考价值。

关键词：色散曲线；Ka波段过模慢波结构；数值计算算法

在高功率微波源器件的设计和研制过程中，需要了解其慢波结构的色散特性。慢波结构色散关系的场匹配解法已经发展得较为完善[1-4]，但是在高频段(例如，频率高于30GHz)大过模比情况下，采用通用方法推导得到的色散方程数值计算较为困难。本文针对Ka波段慢波结构的特殊情况，推导了一种针对高频段轴对称慢波结构快速有效的色散特性求解方法。该方法在边界处直接积分计算，没有通用算法中傅里叶级数展开，在保证一定计算精度的前提下，简化了计算过程，提高了计算速度。

1理论推导

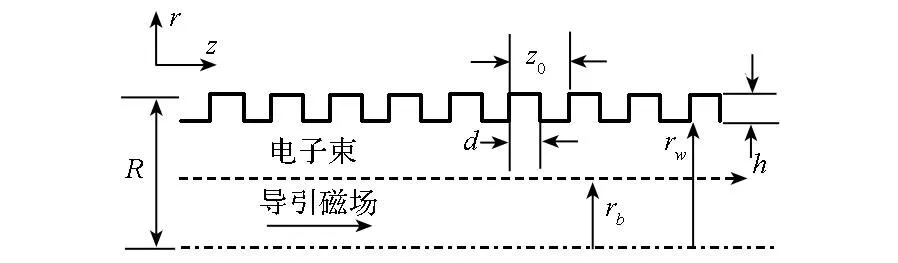
如图1所示，本文采用的慢波结构为具有矩形截面的轴对称盘荷结构。此种类型的慢波结构常用于高频段微波源中[5-9]，具有结构简单、加工容易的优点。慢波结构的基本尺寸参数为：漂移管的半径R，慢波结构的周期Z0，高度h，盘荷间距d，电子束半径rb。由于慢波结构器件中几何机构和电子束的圆周对称特性，参与束波相互作用的主要是具有圆周对称的结构和轴向电场分量的TM0n模式，这里仅讨论这些模式的色散特性。为了简化计算，做如下几点合理假设：慢波结构轴向无限长，所分析区域内的任意点可以认为距离场源无限远；轴向约束磁场无穷大，电子束仅有沿z方向的一维速度分量；电子束的厚度忽略不计，但是具有有限大的总电流Ib；忽略各个场分量和电子束参量的高阶扰动量，如电子速度v=v0+v1。

TM0n模式仅有轴向电场Ez、径向电场Er和角向磁场Hφ三个不为零的场分量。根据Floquet定理，轴向电场分量可以分解为级数展开的形式[10]

(1)

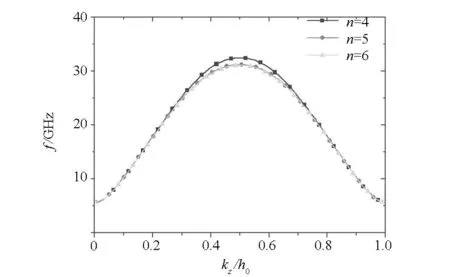
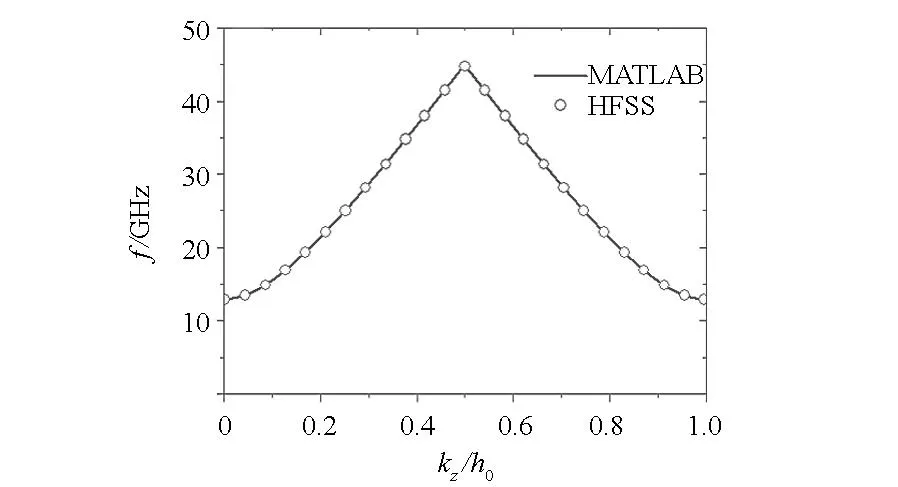
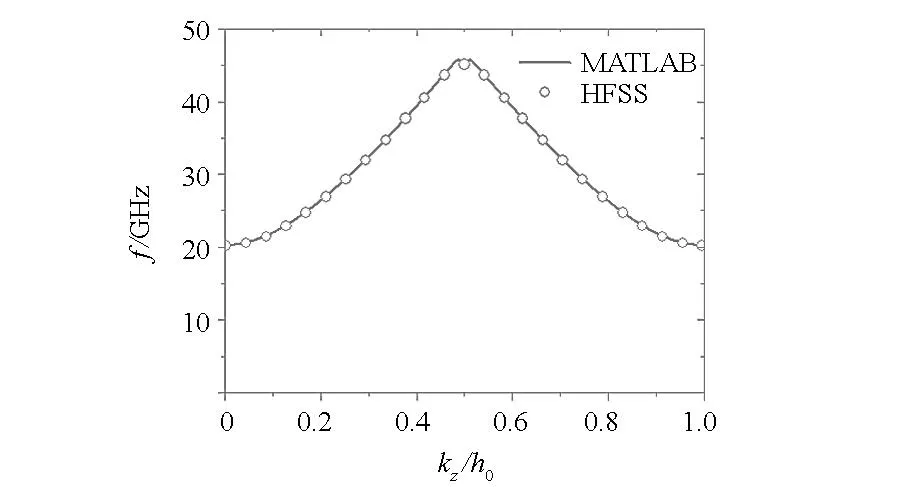
式中kn=k0+nh0, h0=2π/z0, -h0/2≤k0

图1　具有矩形截面的轴对称慢波结构示意图Fig.1　Diagram of axial symmetric SWS with rectangular section

求解区域的各次谐波的轴向电场Ezn满足Maxwell方程组，整理可得

(2)

式中Γn2=ω2/c2-kn2。

其他场分量可以用轴向电场分量表示

(3)

(4)

式(2)的基本解形式为

(5)

其中J0(x)为零阶第一类Bessel函数。在波导壁处需满足切向电场为零的边界条件

(6)

其中Rw(z)为z处的波导壁半径。在电子束处的边界条件为[1]

(7)

结合边界条件式(6)和式(7)，式(5)可以整理为矩阵的形式

D·A=0

(8)

其中

det(D)=det[Dmn]=0

(9)

式(9)即是慢波结构的色散方程。

2数值求解方法

编制了MATLAB计算程序，数值求解色散方程，求解步骤如下。

1)对基波轴向波数k0取一系列离散值，据此确定各次谐波的轴向波数kn=k0+nh0；

2)对各个k0，使用二分法[4]求解ω的值；

3)每个k0，有多个不同的ω解，将它们按从小到大的顺序加注标记ω(1),ω(2),…ω(n)，则数组(k0,ω(1))为TM01模式色散曲线上的点，数组(k0,ω(2))为TM02模式色散曲线上的点，……数组(k0,ω(n))为TM0n模式色散曲线上的点；

4)依次连接不同k0取值对应的所有(k0,ω(n))，构成TM0n模式色散曲线。

图2　不同矩阵阶数下的色散曲线(以TM01为例)Fig.2　Dispersion curves in different matrixranks (take TM01as an example)

在计算色散矩阵D时，我们取的矩阵阶数为5～7阶，具体阶数的确定原则是：逐次增大矩阵阶数，直到相邻两种阶数下求解得到的色散曲线偏差在1%以内。例如图2所示为矩阵阶数分别取4，5和6阶时TM01模式的色散曲线示意图，可以看出矩阵取4阶时色散曲线与取5阶时偏差较大，而取5阶和取6阶时偏差较小。综合考虑准确性和计算时间，可以取5阶矩阵进行计算。本方法由于处理波导壁处边界时，没有采用常见的傅里叶展开拟合边界形状的方法，而是直接将边界形状函数代入求解，简化了计算过程。

3计算结果和相关讨论

选取Ka波段高功率微波源[5]的一组典型尺寸参数(具体参数值见表1)，数值计算了其色散特性。

表1Ka波段高功率微波源的典型尺寸参数

Tab.1ParametersoftheKa-bandHPMdevice

(mm)

如图3所示，是计算得到的TM01,TM02和TM03模式的色散曲线，通过与高频电磁仿真软件HFSS计算得到的同样尺寸参数条件下的色散曲线进行对比，发现二者吻合较好，相对误差小于2%。值得指出的一点是，使用高频电磁仿真软件计算色散曲线建模比较烦琐，而且由于计算区域相对于微波波长较大(结构直径约为波长的4～5倍)，剖分网格数目巨大，计算耗时较长。

(a) MATLAB数值计算得到的TM01,TM02和TM03模式的色散曲线(a) Dispersion curves of TM01, TM02and TM03(MATLAB)

(b) 模式数值计算结果与软件计算结果的对比 (TM01)(b) Result comparison between MATLAB and softwaresimulation (TM01)

(c) 模式数值计算结果与软件计算结果的对比 (TM02)(c) Result comparison between MATLAB andsoftware simulation (TM02)

(d) 模式数值计算结果与软件计算结果的对比 (TM03)(d) Result comparison between MATLAB andsoftware simulation (TM03)图3　MATLAB数值计算得到的色散曲线Fig.3　Result dispersion curves calculated by MATLAB program

4结论

本文理论推导了一种计算色散特性的数值方法，并据此编制MATLAB数值程序。与商业软件计算结果相比，采用该数值算法编程得到的结果频率相对偏差在2%以内，且大大减少了计算时间。相关计算方法适用于Ka波段微波源结构参数的辅助选取，具有快速、准确的优点。

参考文献(References)

[1]Swegle J A, Poukey J W, Leifeste G T. Backward wave oscillators with rippled wall resonators: Analytic theory and numerical simulation [J]. Physics of Fluids. 1985, 28(9): 2882-2894.

[2]Minami K, Carmel Y, Granatstein V L, et al. Linear theory of electromagnetic wave generation in a plasma-loaded corrugation-wall resonator [J]. IEEE Transactions on Plasma Science. 1990, 18(3): 537-545.

[3]李大治, 杨梓强, 梁正. BWO慢波结构几何参数的研究[J]. 电子科技大学学报. 1998, 27(1): 63-68.

Li Dazhi, Yang Ziqiang, Liang Zheng. Research on geometry parameters of BWO slow-wave structure [J]. Journal of UEST of China. 1998, 27(1): 63-68. (in Chinese)

[4]董烨, 董志伟, 周海京. 含电子束任意轴对称周期慢波结构色散曲线的数值计算[J]. 微波学报. 2007, 23(5): 53-58.

Dong Ye, Dong Zhiwei, Zhou Haijing. Numerical computation of dispersion curves in an arbitrary axial symmetric periodic SWS including an electron beam [J]. Journal of Microwaves. 2007, 23(5): 53-58. (in Chinese)

[5]Zhu J, Shu T, Zhang J, et al. A high power Ka band millimeter wave generator with low guiding magnetic field[J]. Physics of Plasmas,2010, 17: 083104.

[6]Zhang J, Zhong H H, Jin Z, et al. Studies on efficient operation of an X-band oversized slow-wave HPM generator in low magnetic field [J]. IEEE Transactions on Plasma Science, 2009, 37(8): 1552-1557.

[7]Zhang H, Shu T, Ju J C, et al. Gigawatt-class radiation of TM01mode from a Ku-band overmoded cerenkov-type high-power microwave generator[J]. IEEE Transactions on Plasma Science,2014, 42(6): 1567-1572.

[8]Wu D, Shu T, Zhu T, et al. Mode composition analysis on experimental results of a Gigawatt-class Ka-band overmoded Cerenkov oscillator [J]. Physics of Plasmas, 2014, 21:073105.

[9]Li X, Song Z, Wang J, et al. Design and numerical simulations of a high power 0.15 THz oscillator [J]. Physics of Plasmas, 2012, 19:083111.

[10]Watanabe T, Choyal Y, Minami K, et al. Range of validity of the rayleigh hypothesis. [J] Physics Review E,2004, 69(5):056606.

Numerical computation of dispersion curves in the Ka-band overmoded slow wave structure

WUDapeng,SHUTing,ZHANGHua

(College of Optoelectronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：Backward wave oscillator with over-mode Ka-band high power microwave (HPM) generally outputs mixed TM0n modes, it has high energy conversion efficiency, but it can′t ensure the purity of output modes. However, it is necessary for high radiation efficiency that the microwave input to the radiation terminal is certain single and pure. So it is hard to put these HPM sources into application. In order to solve this problem, a design method for compact hybrid modes converter of purifying TM0n mixed modes was proposed. With this method, the TM01, TM02 and TM03 mixed modes can be converted into pure circular waveguide TM01 mode efficiently on the condition of high power capacity and wide wave band. This method also reduces the modes purification difficulty in the design of the HPM sources.

Key words：dispersion curve; Ka-band overmoded slow-wave structure; numerical computing method

中图分类号：TN12

文献标志码：A

文章编号：1001-2486(2015)02-028-04

收稿日期：2015-01-05基金项目：国家自然科学基金资助项目(11075211)

作者简介：武大鹏(1988—)，男，山东沂水人，博士研究生，E-mail：vipbenjamin@163.com；舒挺(通信作者)，男，教授，博士，博士生导师，E-mail：mrtingshu@qq.com

doi:10.11887/j.cn.201502007

http://journal.nudt.edu.cn