判断聚合的可接受性问题研究*

梁 庆 寅， 李 一 希



判断聚合的可接受性问题研究*

梁 庆 寅， 李 一 希

摘要：重点讨论群体决策的理性可接受性问题。在以讨论“可行能力”为核心的理性选择理论范畴下，提出了一种群体理性可接受性的概念，它既避免了将群体作为个体抽象物进行重建的弊端，又对经典的群体判断聚合困境提供了比较合理的解决途径；但同时发现，这样的群体理性条件导致一些违反人们群体决策常识的问题出现，比如，它为少数决定制的群体决策规则做出了合理性辩护。进一步刻画群体决策规则合理性和群体决策结果合理性之间的不一致性，对于判断聚合理论、协商民主理论，以及如何在多元社会现实背景下实现共识具有积极的理论意义和现实意义。

关键词：判断聚合； 可接受； 妥协； 可行能力

一、导言

当一群人在讨论一件事情，并需要做出决定的时候，人们常常会考虑这样的问题：群体做出的决定是否被这个群体成员所接受，或者说群体愿意接受一项决定的条件是什么。比如进行立法，由一个委员会讨论并决定是否通过一项法律条款，需要考虑一项法律条款能否被委员会所接受并通过，甚至要考虑它能否被社会公众所接受。

可接受性主要是衡量某一个对象在何种程度上被主体肯定或认同的概念，在哲学、政治、法律、经济等人文社会科学领域被广泛讨论。无论在何种科学领域研究可接受性，有一点是被普遍认可的，即客观事实是必须被接受的。这样就存在一个重要的基本问题：当事实发生之前，理性的人如何去接受它。许多情况下，人们需要讨论尚未发生的事情是否可接受。由于基于命题构建的逻辑公理系统能够为没有成为事实之前的命题做出辩护，因此，哲学家和认知科学家们从20世纪50年代开始将命题作为可接受性的对象展开研究，主要讨论理性的人究竟什么时候应当接受一个命题。卡普兰(Mark Kaplan)是其中的代表性学者，他最早提出了个体对命题接受的理性公理系统*Mark Kaplan, Rational Acceptance,Philosophical Studies, 1981,pp.129—145.。从21世纪初开始，在利斯特(Christian List)、迪特里希(Franz Dietrich)等学者努力下，以讨论判断聚合困境(Discursive Dilemma)为核心的群体判断聚合理论得到快速发展*Christian List ,The theory of judgement aggregation:an introductory review,Synthese, (2012)187:179—207.，由此也产生出理性可接受理论的新问题：群体关于命题的理性接受该如何刻画。很多学者针对这一问题展开了讨论，有代表性的包括都文(Icor Douven)和罗曼金(Jan-Willem Romeijn)提出了个体等级的可接受性与群体等级的可接受性存在相似性*Icor Douven,Jan-Willem Romeijn,The Discursive Dilemma As A Lottery Paradox,Economic and Philosophy，(2007)23:301—319.；钱德勒(Jake Chandler)详细讨论了利用概率刻画个体可接受性的方法以及相关性质，并在此基础上首次给出了群体可接受性公理系统*Jake Chandler,Acceptance,Aggregation and Scoring Rules,Erkenntnis，(2013)78:201—217.。这些理论的共同点在于将群体可接受与个体可接受进行了类比，构建了一种与个体可接受理论相似的群体可接受理论，而这样将群体作为个体抽象物进行重建的做法，又是被森(Amartya Sen)等人在讨论群体理性时所极力避免的*Amartya K.Sen,The Idea of Justice,London:Penguin-Allen Lanes，2009.。

本文将在森提出的应当关注“可行能力(Capabilities)”的理性选择理论*Amartya K.Sen,The Idea of Justice,London:Penguin-Allen Lanes，2009.范畴下提出一种群体理性可接受性的概念。它既避免了将群体作为个体抽象物进行重建的弊端，又对经典的群体判断聚合困境提供了比较合理的解决途径。但同时发现，这样的群体理性条件也会导致一些违反人们群体决策常识的问题出现，比如，它为少数决定制的群体决策规则做出了合理性辩护。

本文的第2部分将提出个体妥协性与判断聚合困境的关系；第3部分将在“可行能力”理论基础上构建一种新的群体理性可接受性条件，将证明在此基础上，确实能为判断聚合困境提出新的解决途径；第4部分将证明这种群体可接受性条件会给群体理性带来一些新的问题，比如它为少数决定制的群体决策规则做出了辩护；第5部分是结论。

二、个体判断的妥协性与判断聚合困境

(一)关于判断聚合困境一种新的认识

首先从判断聚合困境经典的例子开始。假设有一个3人组成的立法委员会，它做出是否通过一项法令的决定主要基于其成员对一组命题的理性判断，每个成员需要对以下三个命题进行判断：

p：“土地资源是有限的。”

p→d：“如果土地资源是有限的，那么应当立法严禁土葬。”

d：“应当立法严禁土葬。”

通常在立法委员会里对三个命题的判断有三种比较典型的意见。一个是坚定的支持者，他的立场是要求立法禁止土葬，给出的理由是他认为上述三个命题都是成立的。还有一个是强硬的反对者，他反对“禁止土葬”，也认为土地是有限的(即赞同p)，但出于风俗习惯的考虑，他不认为土地资源有限就应该禁止土葬(即反对p→d)，得出的结论是不应该通过立法禁止土葬(即反对d)。另有一个是态度比较温和的，他虽然也认为不应该禁止土葬，但给出的理由是土地资源并非有限(即不接受p)，他同意在土地有限的情况下应该禁止土葬(即接受p→d)。三类意见的表达见表1。可以看到支持者、反对者和态度温和者三个人的判断都是一致的，但用多数制规则聚合的时候结论却出现了不一致，也就是基于前提的多数聚合规则得到的结果与直接在结论上运用多数聚合规则得出的结果不一致，这就是判断聚合困境。

表1　判断聚合困境

表2　妥协后的判断聚合

如果允许个体判断对命题的取值进行合理的变动，我们能够对判断聚合困境产生的原因给出一些新的解释。对于态度温和者来说，假设他对结论d的判断是通过前提导出的，那么我们将他对结论d的判断改为“真”是存在合理性的，因为做出这样的修改后他的判断集仍然保持一致(见表2态度温和者行)，运用多数规则可以得到群体一致的判断集合(见表2多数规则聚合1)。同理，如果支持者对土地是否有限并不完全确定而改变对该命题的判断(见表2支持者行)，也可以得到群体一致的判断集合(见表2多数规则聚合2)。由此可见，当群体中部分个体在一些命题上做出“妥协”后，可以通过多数制规则聚合得到一致的群体判断集。更进一步的，如果我们将能够经得起群体成员的批判性审思作为群体理性要求*见Amartya K.Sen, The Idea of Justice,London:Penguin-Allen Lanes,2009. 森提出的批判性审思，强调个体对自我信念的反思。在判断聚合中，个体的批判性审思可以理解为个体对在每个命题上是否可以妥协的思考和评判，这种评判更多的是在逻辑意义上的，因此评判是对个体判断的澄清。，那么可以认为个体判断在命题上的不可妥协性则是刻画群体理性可接受性的基础。

(二)基本符号和定义

迪特里希引入了一些(L,├ )系统上的公理*Franz Dietrich,A generalized model of judgement aggregation,Social Choice and Welfare，(2007)28:529—565.，在本文的讨论中认为以下三个公理是成立的：

公理1(自后承) 对任意的φ∈L, φ├φ。

公理2(单调性) 对任意的φ∈L 并且A⊆B⊆L,如果A├φ那么B├φ。

公理3(完全性) 空集Φ是一致的,并且每一个一致的集合A⊆L有一个极大一致集B⊆L包含了每一对φ,φ∈L中的元素。

由公理2易证下列命题：

命题1对∀A⊆L, 如果A一致，A的任意子集是一致的。

接下来，我们开始引入群体聚合的一些基本概念*Christian List ,The theory of judgement aggregation:an introductory review,Synthese, (2012)187:179—207; Klaus Nehring,Clemens Puppe,Consistent judgement aggregation:the truth-functional case,Social Choice and Welfare，(2008)31:41—57.。议程是一个由待决定命题组成的集合，用Z表示，Z是L上的非空有穷子集，且是自身的否定闭包。判断J是议程的子集J⊆Z，且满足(1) J*=Z*，此时也称J具有完全性，即对∀φ∈Z,φ∈J或φ∈J,和(2) J是一致的，即J是L上的一致集(在命题逻辑意义上)。在本文不特别说明情况下，约定判断J是一致且完全的。由公理3和命题1易证下列命题：

命题2对议程Z上的每一个一致子集B,总有一个判断J⊆Z使得B⊆J。

下面我们给出本文最重要的概念——判断妥协性的定义：

对于∀φ∈J，如果J在φ不可妥协，显然有J/φ├φ。对于议程Z上的一个序组P，如果其中存在判断具有妥协性，则称该序组具有妥协性。如果议程Z上还存在一个序组P′,并且P′ 和P中不同的判断两两互为妥协判断，则称P′ 和P 互为妥协序组。

(三)基于妥协的判断聚合困境分析

在多数决定制判断聚合规则下，可以看到，当序组具有妥协性的时候，并不一定会出现群体判断不一致的情况，也就是说个体判断的妥协性不是群体判断不一致的充分条件，而且这种情况是平凡的，比如群体中所有人都持有具有妥协性的判断(如表2中都持支持者观点)，按照多数规则，最后的群体判断当然是一致的。我们接下来将讨论序组的妥协性是否能构成判断困境的必要条件。首先需要对议程做一些约束。

性质1(决议确定性)对于∀φ∈Z，如果∃Ji⊂Z，Ji不具妥协性且φ∈Ji，则∀Jj⊂Z，如果Jj具有妥协性并且φ∈Jj，那么Jj在φ可妥协。

性质2(决议平稳性)对于∀φ∈Z，如果∃Ji⊂Z，Ji不具妥协性且φ∈Ji，则∃Jj⊂Z，Jj具有妥协性，并且Jj在φ不可妥协。

议程的决议确定性的直观意思是如果一个议程存在一个判断坚定地(不可妥协地)支持一个命题，那就不需要再有态度弱一些的判断来支持该命题。议程的决议平稳性的直观意思是如果一个议程存在一个判断坚定地(不可妥协地)支持一个命题，那么至少存在其他判断不那么坚定地(可妥协地)支持该命题的否定。根据这两条性质可以得到如下命题。

命题3如果议程Z具有决议确定性和平稳性，则Z上最多只有一个不可妥协判断。

证明:不妨假设议程Z上有一个不可妥协判断J1。如果还存在其他不可妥协判断，则一定∃φ∈Z，有φ∈J1和φ∈J2，其中J2也不可妥协。由Z具有决议平稳性，则∃具有妥协性，且在φ上不可妥协，在φ上不可妥协。又由Z具有决议确定性，由φ∈J1，有∀J⊂Z,如果J具有妥协性，且φ∈J ,则J在φ上可妥协，与∃具有妥协性，且在φ上不可妥协矛盾。

为了进一步讨论群体判断理性与个体判断妥协性的关系，我们必须引入群体判断聚合规则F的若干理性条件，这些条件最早由阿罗(Arrow K)*Arrow K,Social choice and individual values.New York,NY:Wiley,1951.在偏好聚合理论中提出，后经过利斯特，迪特里希，佩蒂特(Pettit P)等人引入判断聚合理论*Christian List ,The theory of judgement aggregation:an introductory review,Synthese,(2012)187:179—207；List,C.Pettit,P.,Aggregating sets of judgements:Two impossibility results compared.Synthese,(2014)140(1—2)：207—235；Franz Dietrich,Christian List,Propositionwise judgement aggregation:the general case,Social Choice and Welfare,(2013)40：1067—1095.。第一条性质全域性，要求判断聚合规则能够接受由一致且完全的个体判断构成的所有序组。

性质3 (全域性)判断聚合规则F的定义域是由议程Z上所有一致且完全的判断可能构成的序组的集合。

第二个性质是集体理性，限制聚合规则的输出，要求对每一个可能的序组，判断聚合都能得到一个一致并且完全的群体判断。

接下来的性质是一致同意性，表达的是如果群体里所有个体持有相同的判断，那么这个判断也将是群体的判断。

由命题3可证的得下列定理。

定理1表明当议程满足决议确定性、平稳性时，个体判断的妥协性构成了群体判断不一致的必要条件。也就是说如果序组是不可妥协的，只要聚合规则满足一致同意性，就能够得到满足集体理性的群体判断。事实上，同时要求完全一致的集体理性是一个比较强的要求，在很多实际的群体决策中，并不要求群体对所有命题做出判断，也即完全性是不必要的*Franz Dietrich,Christian List,Judgement aggregation without full rationality,Social Choice and Welfare，(2008)31:15—39.此文有对不具有完全性的判断聚合规则的讨论。，比如表2的例子，结果只需要在是否严禁土葬这样一个命题上做出判断。接下来我们将在个体妥协的基础上构建群体可接受性，并以之代替完全性条件，探讨解决判断聚合不可能性定理的途径。

三、群体理性可接受与可能性定理

(一)一种新的群体理性可接受性

引言部分提到都文、罗曼金和钱德勒等学者提出的群体可接受理论的共同点是都以经典概率论为基础，这一类理论给出了一种容易被接受的刻画群体可接受性的模式，但其被接受的原因恰恰是我们需要避免的。这一类理论将群体做了主体化的处理，仿照个体可接受的模式构建了群体可接受。这种将“群体”作为个体抽象物进行重建的处理方式看似合理，但实际上，从马克思(Karl Heinrich Marx)到森，在讨论社会群体问题时，都极力避免以个人的思考方式来考量群体的意志，明确反对将群体作为个体抽象物进行重建的做法*Amartya K.Sen,The Idea of Justice,London:Penguin-Allen Lanes,2009.。为此，我们必须对群体理性可接受性进行重新考虑：一方面，它必须考虑个体的评价；另一方面，它又应当区别于个体的可接受性，符合群体理性的特点。

森提出的“可行能力”理论为我们构建新的群体理性可接受性提供了一种范式。“可行能力”的核心思想是对选择合理性的评价不从效用或资源的角度展开，而是评价个体是否有做出更好选择的能力。例如，在评价教育是否公平的时候，我们也许很难对优质教育资源的分配结果是否公平做出评判，因为持有不同评价标准的人对公平的认识可能完全不同，平等主义者会支持最穷的人群，自由主义者可能会支持教师应当拥有更多资源*自由主义者给出的理由是教师的劳动提供了教育的机会。，但是我们可以将每个个体拥有选择更好教育的机会作为是否公平的评价标准。在这一点上，尽管持有不同的理性审思标准，我们也能在公平的评价上达成一致。

根据“可行能力”的思想，在讨论群体可接受性时，我们考虑的重点不是寻找一种方法来直接评价一个结果是否被群体所接受，而是关注一个命题如果作为群体判断的结果，它是否保持被群体接受的“能力”。从另一角度讲，要评价的是群体是否有不接受一个结果的可能性。换句话说，即便我们无法判断一个结果是否应该被群体接受，但至少能够把明确被质疑的命题排除在群体判断以外。据此，我们提出群体理性可接受定义如下：

定义2 (群体可接受)对于∀φ∈Z，当群体中个体判断构成的序组P中没有判断在φ不可妥协，我们就说表达出序组P这个群体理性接受φ，记作，即∀Ji∈P，若φ∈Ji，则Ji在φ上可妥协当且仅当。

这个定义的直观含义就是当群体中没有人能对一个命题提出无法反驳的反对意见的时候，这个命题就是被群体所接受的。从这个角度理解群体可接受性，一方面考虑到了个体关于命题的评价，群体中每个个体关于命题的判断有可能影响该命题是否被群体所接受；另一方面，群体的可接受性与个体的妥协性和不可妥协性不存在结构上的相似性，也就是说，我们没有把群体看作个体的某种抽象，而是从群体是否具有否定一个命题的能力来评价命题是否被群体所接受。据此，我们提出群体判断聚合规则新的理性条件，要求群体判断的命题是可接受并且一致的。

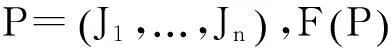
(二)群体理性可接受的可能性定理

如果我们承认群体理性条件是可接受性，可以发现，在经典判断聚合理论里面证明的不可能性定理将能够得到可能性的结论。首先进一步引入几条判断聚合规则的理性条件。

第一个性质是匿名性，表达的是判断聚合中所有个体的权重是一样的。

接下来这个性质是系统性，表达的是命题是否被聚合得到，只与它在序组中的相对位置有关。

最后一条性质比较直观，群体里不存在一个独裁者；独裁者的意思是无论何种情况下，他的判断就是群体的判断。

利斯特和佩蒂特首先证明了判断聚合理论的第一个不可能性定理*C.List,P.Pettit,Aggregation sets of judgements:An impossibility result,Econ.Philos,(2002)18：89—110.，该定理表明当议程满足某些条件的时候，上述一些性质之间是不相容的，如下：

波利(PaulyM)和希斯(van Hees)证明了在上述定理中，如果删除匿名性条件，这样的判断聚合规则是存在的，但它是独裁的*Christian List ,The theory of judgement aggregation:an introductory review,Synthese, (2012)187:179—207.。接下来我们将证明，如果将群体理性的要求调整为集体理性可接受，并将系统性修改为群体判断仅与序组中不可妥协命题结构有关，将能够构造出非独裁的判断聚合规则。

我们可以得到下面可能性定理。

定理3若议程Z满足决议确定性、平稳性，并且Z上存在不可妥协的判断，则存在判断聚合规则同时满足全域性、集体理性可接受性、系统性*、匿名性和非独裁性。

显然Fa满足全域性，由于在要求全域性的条件下Fa并不是完全的，所以它也满足非独裁性。根据Fa的定义，它也是满足匿名性和可接受性的，现在我们只需证明它满足系统性*，并且对于Z上任意的序组P，Fa聚合的群体判断都是一致的。

(1)证明Fa满足系统性*

(2)证明Fa在Z上总是聚合得到一致的判断

由Z满足决议确定性和平稳性和Z上存在不可妥协判断，由命题3，Z上仅有一个不可妥协判断，可令其为Jk。我们假设Fa(P)不一致，则∃φ∈Fa(P)，∃A⊆Fa(P)，A是一致的，且A├φ，由命题2 可得Z上存在一个判断J′，J′在φ不可妥协，且A⊆J′。

(i)若J′是Jk，则由φ∈Fa(P),所以J′∉P，又由A⊆Fa(P)，且A⊆J′，由Z满足决议确定性有J′∈P，产生矛盾。

(ii)若J′不是Jk，则J′具有妥协性，又J′在不可妥协，由Z满足决议确定性，有φ∈Jk，所以Jk∈P，由Fa定义，Fa(P)⊆Jk，则由命题1，Fa(P)一致，与假设矛盾。

由(i)(ii)，这样的J′不存在，所以Fa(P)总是一致的，定理得证。

定理3说明我们给出的群体理性可接受概念，能够为人们理性的群体决策做出一种合理性的辩护。下一节将证明这种群体理性也会导致违反常识的问题，它为少数制群体决策规则提供了辩护。

四、群体理性可接受的困境

首先我们将证明个体妥协性与群体可接受性没有直接的关系，可以得到如下命题：

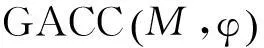
性质11 (稳定性)对∀φ∈Z,对Z上任意的序组P，φ∈F(P)，则对∀Ji∈P ，若Ji在φ可妥协，则将φ换成φ后得到P′ ，有φ∈F(P′)。

稳定性的直观意思是个体妥协不影响群体判断。稳定性还表达了这样的意思，群体的判断应该能经受适当的质疑。实际生活中有很多类似例子，比如在对美国一些典型案件审判结果的讨论中，经常可以看到这样的研究结论：如果陪审团的构成改变，嫌疑人是否有罪的判决结果可能改变。如果将陪审团关于是否有罪的最终判定看作是群体判断的结论，那么这种“陪审团构成改变将会改变判决结果”的观点其实是在质疑群体判断结论的稳定性，这种质疑可以表述为陪审团中某些人对结论并不确定的判断通过投票机制被放大成了群体判断。稳定性的引入会给判断聚合带来新的难题，接下来我们将证明全域性、匿名性、系统性和稳定性将导致判断聚合规则是少数制的。

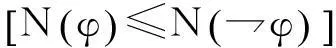
定理4如果一个判断聚合规则F满足全域性、匿名性、系统性和稳定性，那么F是少数制决定方法。

定理4表明了在“可行能力”理论下构建的群体理性可接受性为少数决定制做出了合理性辩护，充分说明了群体决策的复杂性。同时也给我们这样的启示：在群体判断聚集的过程中，我们有必要花费大量的时间和精力去澄清群体中每个个体对议程中每个命题的判断，在处理可以妥协的命题时尤其需要小心，应当为必须由群体做出判断的命题构建不可妥协的个体判断集合，并在群体中形成共识，这些做法都有利于达成我们所追求的群体理性。

五、结论

本文主要在判断聚合理论中引入了判断可妥协的概念，并证明了个体的妥协性构成了判断聚合困境的必要条件。在此基础上，我们利用森的“可行能力”理论，提出了新的群体理性可接受性条件，并证明了在对群体理性要求是可接受且一致的前提下，则经典判断聚合理论中的不可能性定理有新的解决途径。更进一步，我们继续证明了个体妥协不能改变群体的可接受性，上述新的群体理性可接受性条件为少数决定制做出了辩护，这也违反了群体决策常识。本文的研究进一步揭示了群体理性决策的复杂性，当我们克服一种理性决策困境的同时，又将产生新的不理性因素。

从总体上看，本文在为解决判断聚合困境提供方法的基础上，提出并刻画了群体决策中一种关于可接受性的困境，即少数决定制与群体决策结论的理性可接受之间是相互协调的。一方面，群体决策结论的可接受性仅仅与个体不愿意妥协的判断有关，更多的关注群体中每个个体坚定支持的判断对于改善群体决策的可接受性是有利的。因此，当我们在进行群体决策过程中，应当尽可能的引导每个个体更清晰的表达自己不可能改变的判断，这是群体理性的重要前提，在此基础上进行的群体表决*群体表决指判断聚合规则，可以是多数制的举手表决，也可以是其他聚合群体中每个个体判断的一种方法。将更有利于形成一致的群体意见。另一方面，完全忽略个体可妥协的判断又将导致少数决定制，也就是说当我们在进行群体决策的时候，群体中没有明确反对的意见就表示被群体所接受这样一条规则实质上将导致少数决定制，而在实际的群体决策中少数决定制通常被认为是不民主的，采取这样规则得到的群体判断也是不可接受的。这种两难境况的形成，本质上还是由人们对群体决策理性认识的复杂性造成的，也就是说我们需要思考到底是更应该关注群体决策规则的合理性，还是更关注群体决策结果的合理性，这两者往往并不是一致的。从群体决策现实层面来看，本文结论给出的启示是处理好个体可妥协判断和不可妥协判断在群体判断聚合过程中的表达，是改善群体决策可接受性的关键。

(中山大学逻辑与认知研究所文学峰副教授对本文提出过宝贵意见，特此致谢)

【责任编辑：杨海文；责任校对：杨海文，许玉兰】

李一希，中山大学逻辑与认知研究所博士研究生(广州510275)。

中图分类号：B819

文献标识码：A

文章编号：1000-9639(2015)02-0124-08

作者简介：梁庆寅，中山大学哲学系、中山大学逻辑与认知研究所教授(广州510275)；

基金项目：教育部人文社会科学重点研究基地重大项目“广义非形式逻辑研究”(12JJD720006)

收稿日期：*2014—11—12