改进的新老混凝土粘结约束收缩计算模型研究

杨启斌(福建工程学院管理学院，福建福州350118)



改进的新老混凝土粘结约束收缩计算模型研究

杨启斌
(福建工程学院管理学院，福建福州350118)

摘要:引入增量法，提出了改进的新老混凝土粘结约束收缩力学模型。根据相关的实验结果论证该约束收缩力学模型的有效性。最后利用改进的模型对新浇筑自密实混凝土截面上的应力分布情况以及粘结面上的约束剪力进行计算，并对结果进行分析。分析表明，自密实混凝土比普通混凝土因收缩而产生的应力更大，尤其在早龄期;收缩应力不仅会在很大程度上受到自由收缩的影响，而且与混凝土的基本物理力学性能有关。

关键词:约束收缩;新老混凝土粘结;收缩应力;自密实混凝土;计算模型

混凝土的自由收缩不产生应力，但当新浇筑的混凝土自由收缩受到老混凝土的约束，在不受外加荷载的情况下，在新混凝土内部产生了拉应力，在新老混凝土的粘结面上产生了剪应力，这会对结构的承载能力产生不利影响。国内外诸多学者［1－11］进行了新老混凝土粘结性能方面的研究，其中建立约束收缩力学模型可以用来预测由于新混凝土的自由收缩受到老混凝土约束而在新混凝土内部以及新老混凝土粘结面上产生的应力分布，这对混凝土结构加固的承载力和耐久性设计都具有重要的意义。1996年，袁迎曙［10］建立了一个钢筋混凝土结构局部补强中收缩差对结构影响的力学模型; 2001年，刘健［11］建立了约束收缩力学模型，将新老混凝土粘结试件在粘结面处分隔开，分别取新、老混凝土作为独立体进行研究，最后考虑到粘结面处的变形协调和混凝土徐变的影响，列出新、老混凝土在粘结面处的变形协调方程来求解因老混凝土的约束作用而产生的剪应力的合力及横截面的应力分布。

本文在前人研究基础上，提出改进的新老混凝土粘结约束收缩力学模型，并引用相关的试验结果［11］，对该约束收缩力学模型的计算结果的准确性进行论证，然后采用此模型计算出新浇筑自密实混凝土截面上的应力分布情况以及粘结面上的约束剪力，并对计算的结果进行分析。

1　改进的约束收缩力学模型

由于混凝土早期自由收缩发展较快，且混凝土早期各种性能(强度、弹性模量等)还不稳定，都处于发展阶段，随龄期的增加而增长的幅度较大，故本文在文献［11］提出的约束收缩力学模型基础上，采用增量法进行新老混凝土粘结约束收缩应力分析。

将时间t划分为n个时间间隔，即Δt1、Δt2、Δt3、…、Δtn(Δtn= tn－tn－1)，在Δti时间间隔内，新、老混凝土在粘结面上产生的合力的增量为ΔF1i、ΔF2i，两者互为作用力与反作用力，故两者数值相等。

由文献［11］提出的约束收缩力学模型中应力与合力的关系可得:

Δσ1i、Δσ1i为Δti时间间隔内新、老混凝土横截面上的应力增量(Pa) ; y0为距老混凝土横截面形心轴的距离(m) ; y1、y2为粘结界面距新、老混凝土横截面形心轴的距离(m) ; yn为距新混凝土横截面形心轴的距离(m) ; A1、A2为新、老混凝土横截面面积(m2) ; I1、I2为新、老混凝土横截面惯性矩。

考虑了混凝土收缩、徐变的影响的本构关系为:

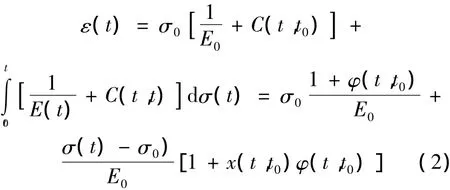
式中，σ0为开始加载时刻的应力; E0为开始加载时刻混凝土的弹性模量;σ(t)为在开始加载后的任一时刻t的应力; E(t)为任一时刻t的混凝土的弹性模量; x(t，t0)为混凝土的老化系数，可以认为是在开始加载以后发生的应力变化所产生的徐变，由于混凝土的老化而逐渐衰减的一种衰减系数，其值总小于1，一般可取为0.8;φ(t，t0)为混凝土的徐变系数。

假定ti－1时刻前各应力增量Δσj(j = 1，2，3，…，ti－1)以恒力作用在各相应的增量步末时刻tj，由此应力增量在Δti内产生的徐变应变Δε(ti，ti－1)为:

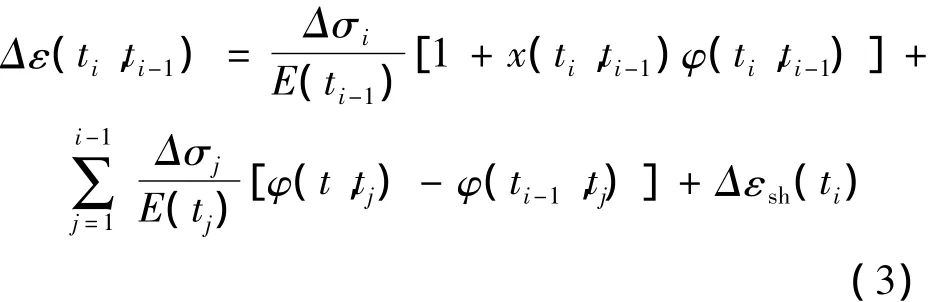
式中，εsh(t)为混凝土在t时刻的自由收缩值。

在新老混凝土界面粘结良好的情况下，一般可近似认为新老混凝土在粘结面上不产生相对滑移现象，因此在Δti时间间隔内，新、老混凝土在粘结面处产生的应变增量协调相等。

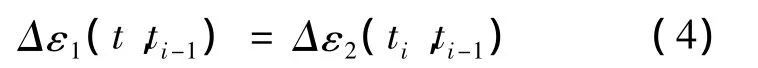
式中，Δε1(t，ti－1)、Δε2(ti，ti－1)为Δti时间间隔内新、老混凝土在粘结面处产生的应变增量。

将合力应力关系式和应力应变关系式代入应变增量协调方程，可得:

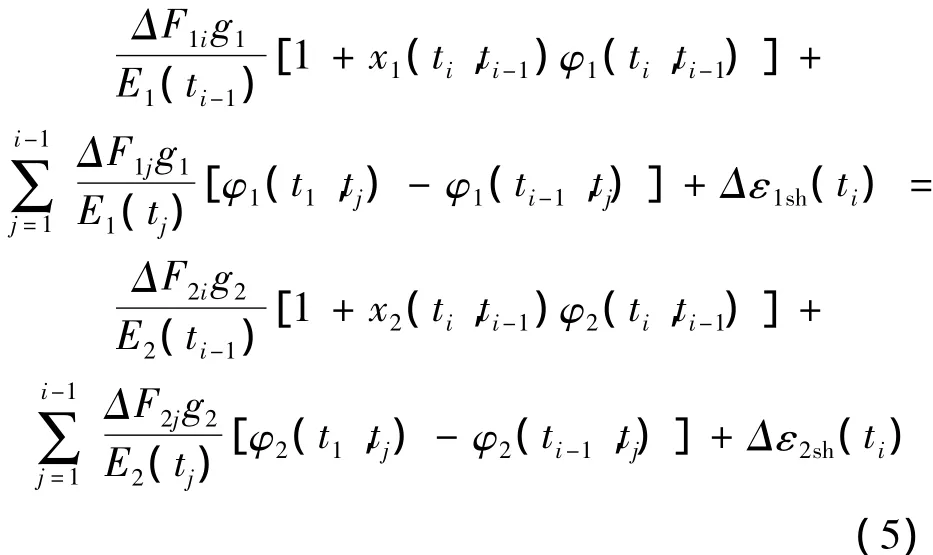
式中，E1、E2为新、老混凝土的弹性模量; x1(titi－1)、x2(ti－ti－1)为新、老混凝土在Δti时间间隔内的老化系数;φ1(ti，ti－1)、φ2(ti，ti－1)为新、老混凝土在Δti时间间隔内的徐变系数;Δε1sh(ti)、Δε2sh(ti)为新、老混凝土在Δti时间间隔内的自由收缩应变值。

混凝土的徐变函数本文采用B3模型［1］，即:

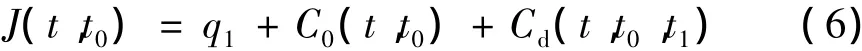
式中，q1为0.6×106/E28; C0(t，t0)为混凝土的基本徐变函数; Cd(t，t0，t1)为混凝土的干燥徐变函数; t0为混凝土开始加载的时刻，t1为混凝土开始干燥收缩的时刻，t1≤t0。

老混凝土收缩已经基本稳定，可忽略老混凝土自由收缩Δε2sh(ti)的影响，又ΔF1i=ΔF2i，故式(6)经过整理可得在Δti时间间隔内由于老混凝土的约束作用而产生的力的增量。

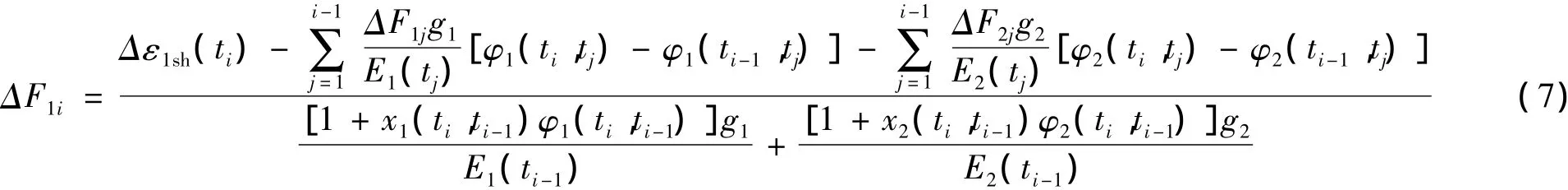
进而可计算出在Δti时间间隔内新、老混凝土横截面上的应力增量Δσ1i、Δσ2i，再计算出ti时刻新、老混凝土横截面上的应力分布σ1(ti) S、σ2(ti)。

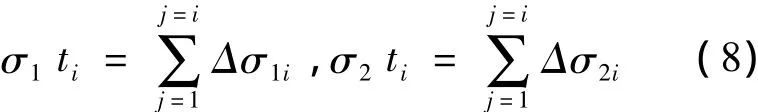
2　模型验证及计算结果分析

2.1模型的验证

本文引用文献［11］的试验成果及其模型计算结果验证所建模型的准确性，试验测点布置图见图1。文献［11］实测收缩应变值、其约束收缩力学模型的理论计算值和改进的约束收缩力学模型的理论计算值如表1所示。其中，在用改进的模型进行计算时，当新混凝土为普通混凝土，E(t) = E0(1－e－0.09t)，E0按规范取值，老混凝土的弹性模量按规范取值;当新混凝土为自密实混凝土，E(t) = E0(1－βe－0.1t)，E0、β按已有试验拟合值来进行取值，徐变模型B3模型来近似代替。

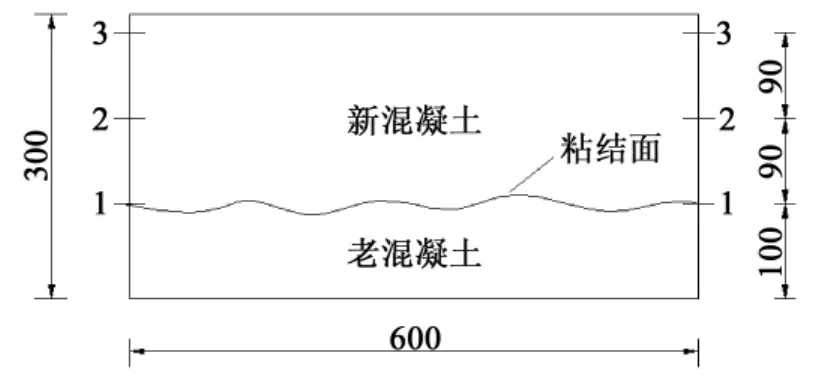
图1　约束收缩测点布置示意图(单位: mm)Fig.1　Surveying points arrangement of restrained shrinkage(unit: mm)

由表1、图2和图3可以看出:收缩应变随新混凝土龄期增加而增长，早期发展较快，随龄期的增加，收缩应变发展越来越平缓，最终将趋向一稳定值。与刘建提出的力学模型计算值相比，改进的约束收缩力学模型计算的结果更接近于试验实测值，其中在测点2，两者的最大误差为9.55%，不超过10%，刘健提出的约束收缩力学模型计算的结果与试验实测值的最大误差为14.02%。

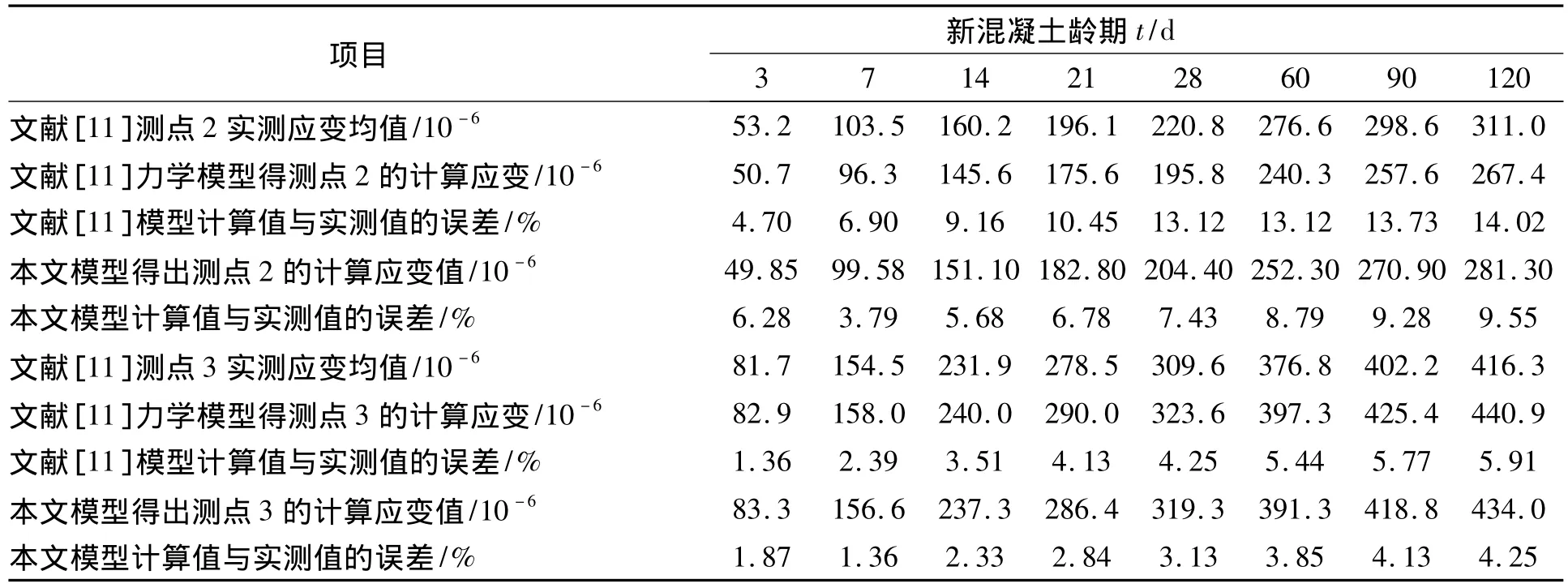
表1　测点2、3处的应变实测值和理论计算值比较Tab.1 Comparison between measured values and calculated values of restrained shrinkage at surveying point 2，3

因此，采用本文的改进的约束收缩力学模型计算所得的计算值与实测值比较吻合，表明改进的模型合适，可以用来进行新混凝土横截面上的应力分布以及新老混凝土粘结面上的约束剪力的计算。

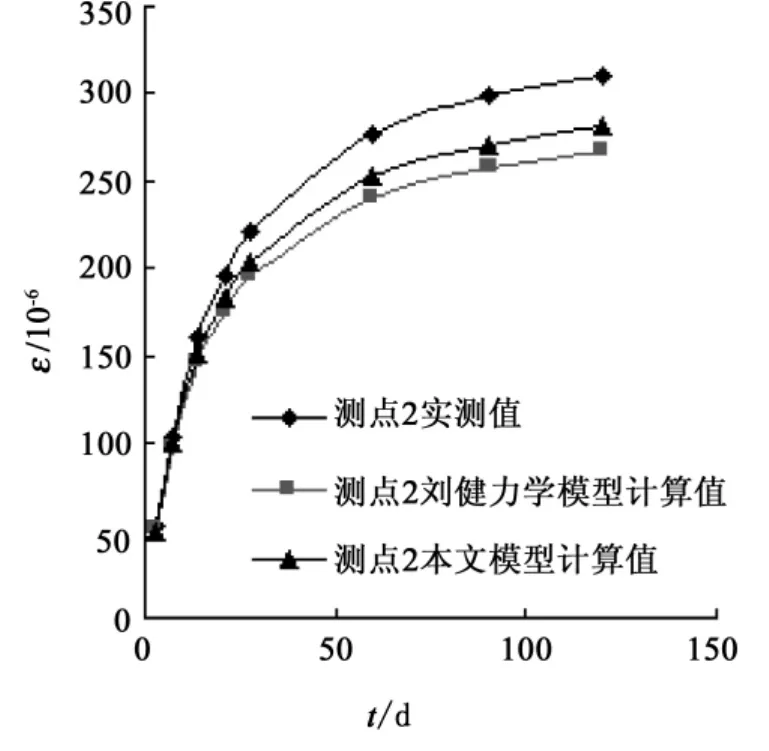
图2　测点2计算值与实测值的比较Fig.2　Comparison between calculated values and measured values at point 2

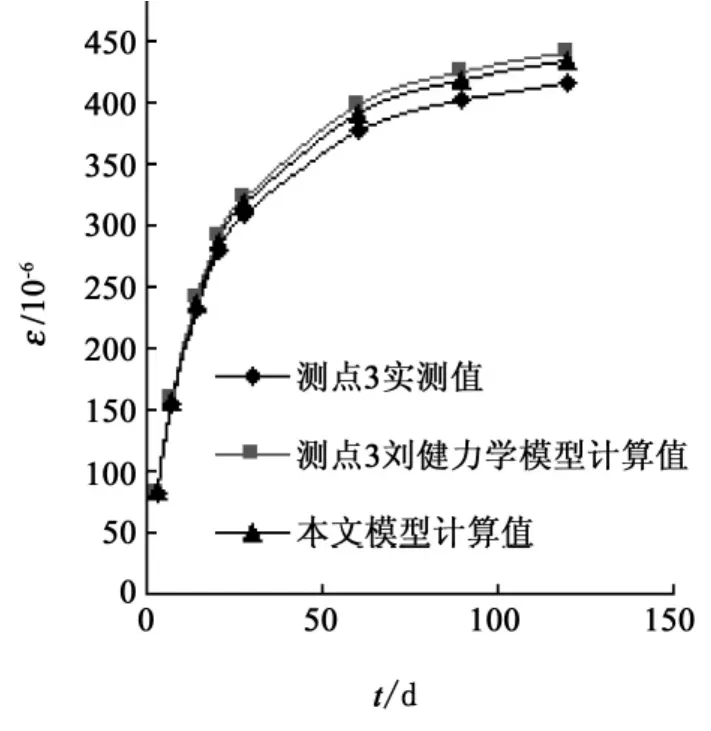
图3　测点3计算值与实测值的比较Fig.3　Comparison between calculated values and measured values at point 3

2.2计算结果分析

采用本文改进的约束收缩力学模型计算出各时刻新混凝土横截面上粘结面处的拉应力和粘结面上的约束剪力F(t)，结果见表2和表3，其中NC代表强度等级为C40的普通混凝土，SCC1、SCC2、SCC3分别代表强度等级为C45、C40、C35的自密实混凝土。

由表2、图4、图5可知:虽然自密实混凝土和普通混凝土强度等级相同，但以它们为新混凝土而制成的约束收缩试件，因收缩而产生的应力相差较大，前者比后者因收缩而产生的应力更大，尤其是在早龄期，3 d、7 d时分别比普通混凝土大了148.6%和77.7%。因为自密实混凝土的自由收缩要比相同强度等级的普通混凝土大得多，特别在早龄期，使得以自密实混凝土由于收缩而产生的应力比普通混凝土更大，虽然前者的弹性模量更小，但对应力的影响不及自由收缩大。

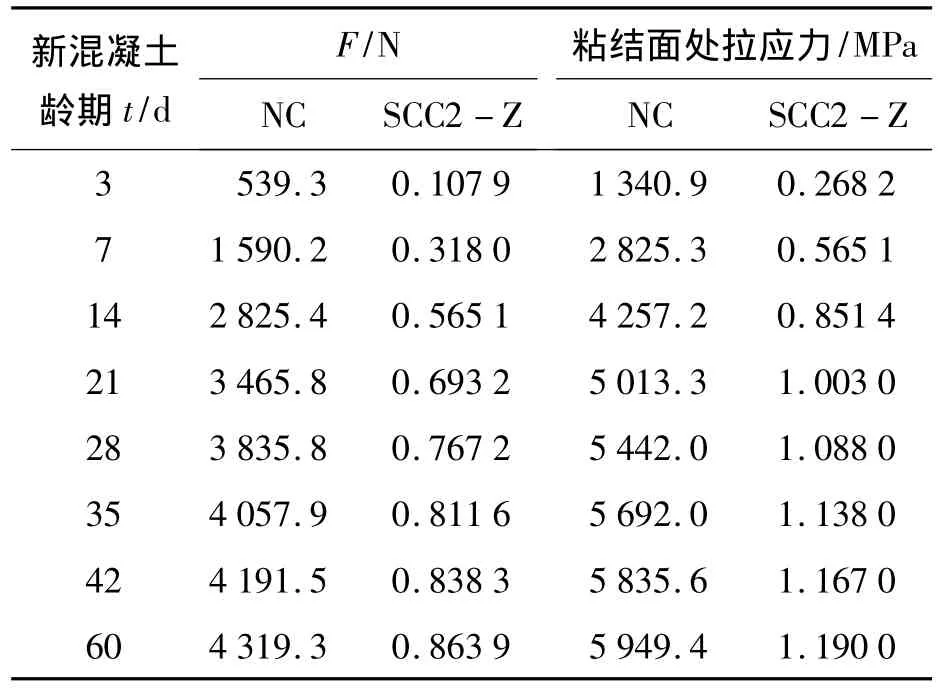
表2　新混凝土为相同强度等级的普通混凝土和自密实混凝土各时刻粘结面上的约束剪力和新混凝土粘结面处的拉应力Tab.2　The adhesive interface restrained shear and interface tensile stress at different ages of young concrete consisting of the same strength grade ordinary concrete and self-compacting concrete

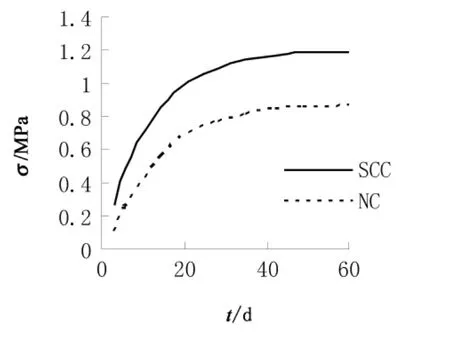
图4　新混凝土为同强度等级普通混凝土和自密实混凝土粘结面处拉应力与时间的关系Fig.4　The relationship between interface tensile stress and time when young concrete consists of the same strength grade ordinary concrete and self-compacting concrete

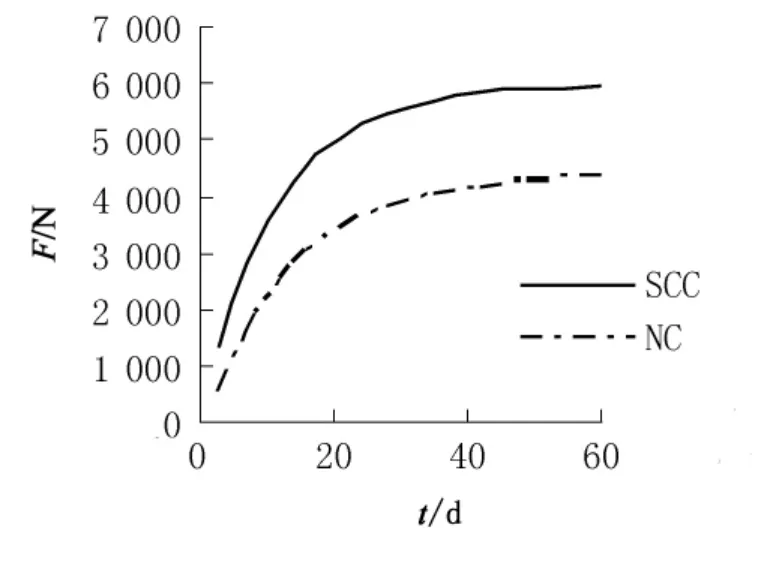
图5　新混凝土为同强度等级普通混凝土和自密实混凝土粘结面上约束剪力与时间的关系Fig.5 The relationship between interface restrained shear and time when young concrete consists of the same strength grade ordinary concrete and self-compacting concrete

表3　新混凝土为不同强度等级的自密实混凝土各时刻粘结面上的约束剪力和新混凝土粘结面处的拉应力Tab.3 The adhesive interface restrained shear at different ages and interface tensile stress at different ages of young concrete consisting of different strength grade self-compacting concrete

由表3、图6、图7可知:不同强度等级自密实混凝土，因自由收缩和物理力学性能方面的差异，使其作为新混凝土因收缩而产生的应力不同。SCC2因其自由收缩最小，故以它为新混凝土而产生在粘结面处拉应力和约束剪力最小，表明自密实混凝土的自由收缩对收缩应力影响很大。再比较SCC1和SCC3，以前者为新混凝土而产生的收缩应力更大，故虽然它们的自由收缩很接近，但它们的物理力学性能有较大差异，SCC3的强度、弹性模量更小，表明自由收缩基本相同时，以强度高、弹性模量大的自密实混凝土为新混凝土时产生的收缩应力更大。

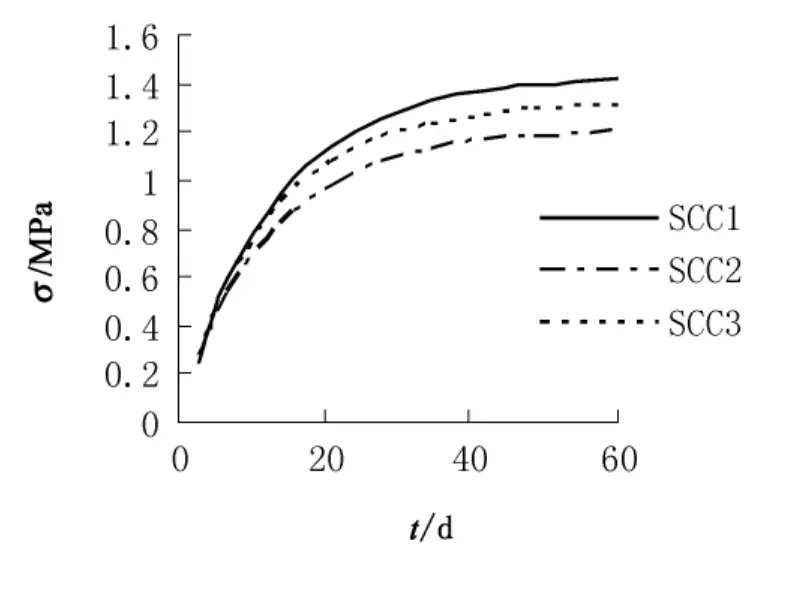
图6　新混凝土为不同强度等级的自密实混凝土粘结面处拉应力与时间的关系Fig.6 The relationship between interface tensile stress and time when young concrete consists of different strength grade self-compacting concrete

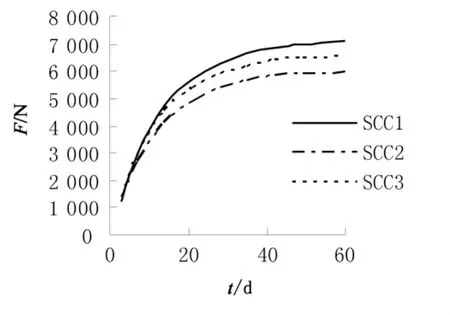
图7　新混凝土为不同强度等级的自密实混凝土粘结面上约束剪力与时间的关系Fig.7　The relationship between interface restrained shear and time when young concrete consists of different strength grade self-compacting concrete

3　结论

1)本文所提出的改进方法能够较为准确计算出新混凝土在粘结面处的拉应力以及粘结面上的约束剪力，相比刘健提出的约束收缩力学模型，改进的约束收缩力学模型计算所得的计算值与实测值更为吻合，表明改进的模型是合理的。

2)由采用本文改进的约束收缩力学模型计算出各时刻新混凝土横截面上粘结面处的拉应力和粘结面上的约束剪力，比较相同强度的自密实混凝土和普通混凝土，可得到自密实混凝土因收缩而产生的应力更大，尤其在早龄期。因此相比普通混凝土，在采用自密实混凝土进行既有结构加固时，更应重视由于收缩而产生的初始应力的影响。

3)在采用改进的约束收缩力学模型的计算结果中，比较不同强度等级的自密实混凝土由于新混凝土收缩而产生的应力，强度等级为C40的

参考文献:自密实混凝土因其自由收缩最小，而使得粘结面处拉应力和粘结面上的约束剪力最小。这表明自密实混凝土的自由收缩对收缩应力有很大的影响。

4)在计算结果中，比较不同强度C45和C35的自密实混凝土为新混凝土而产生的收缩应力，发现强度、弹性模量较大的C45产生的收缩应力更大些。这表明除了自由收缩，自密实混凝土的强度、弹性模量等基本物理力学性能对收缩应力也有一定的影响，在自密实混凝土自由收缩基本相同的情况下，以强度高、弹性模量大的自密实混凝土为新混凝土时产生的收缩应力大一些。

［1］Bazant Z P，Baweja S.Justification and refinements of Model B3 for concrete creep and shrinkage 1.Statistics and sensitivity［J］.Materials and Structures，1995，28(7) : 415－430.

［2］Oluokun A F，Haghayeghi A R.Flexural behavior of reinforced concrete beams retrofitted or repaired with slurry infiltrated mat concrete［J］.ACI Structure Journal，1998，95(6) :654－664.

［3］Bazant Z P.Criteria for rational prediction of creep and shrinkage of concrete［J］.ACI Special Publication，2000，194: 237－260.

［4］Gardner N J，Lockman M J.Design provisions for drying shrinkage and creep of normal-strength concrete［J］.ACI Materials Journal，2001，98(2) :159－167.

［5］Turcry P，Loukili A，Haidar K，et al.Cracking tendency of self-compacting concrete subjected to restrained shrinkage: experimental study and modeling［J］.Journal of Materials in Civil Engineering，2006，18(1) :46－54.

［6］Loser R，Leemann A.Shrinkage and restrained shrinkage cracking of self-compacting concrete compared to conventionally vibrated concrete［J］.Materials and Structures，2009，42(1) :71－82.

［7］Hilaire A，Benboudjema F，Darquennes A，et al.Modeling basic creep in concrete at early-age under compressive and tensile loading［J］.Nuclear Engineering and Design，2014，269:222－230.

［8］陈峰，郑建岚.自密实混凝土与老混凝土的粘结收缩试验研究［J］.厦门大学学报:自然科学版，2009，48(6) : 844－847.

［9］陈峰，郑建岚.自密实混凝土与老混凝土粘结强度的直剪试验研究［J］.建筑结构学报，2007，28(1) :59－63.

［10］袁迎曙.钢筋混凝土结构局部补强的收缩应力分析［J］.土木工程学报，1996，29(1) :33－40.

［11］刘健，赵国藩.新老混凝土粘结收缩性能研究［J］.大连理工大学学报，2001，41(3) :339－342.

(责任编辑:陈雯)

Improved restrained shrinkage calculation model for adhesive concrete

Yang Qibin
(School of Management，Fujian University of Technology，Fuzhou 350118，China)

Abstract:Incremental method was employed to establish a mechnical restrained model for patched concrete.The simulation results confirm the effectiveness of the mechanical restrained shrinkage model.The stress distribution of the concrete and the restrained shear were calculated and analysed with the improved model.The results show that the shrinkage stress of the selfe-compacting concrete is higher than that of the ordinary concrete especially in the early age，that the shrinkage stress is not only affected by the free shrinkage but is relative to the basic mechanical properties of the concrete.Keywords: restrained shrinkage; adhesion between young and old concrete; restrained stress; selfcompacting concrete; calculation model

doi:10.3969/j.issn.1672－4348.2015.01.004

作者简介:杨启斌(1977－)，男(汉)，福建莆田人，硕士，讲师，研究方向:高性能混凝土。

基金项目:福建省住房和城乡建设厅项目(2011－K－22) ;福建省教育厅项目(JA10217)

收稿日期:2014－10－17

中图分类号:TU528

文献标志码:A

文章编号:1672－4348(2015) 01－0022－06