建筑工程投标方案比选方法研究——基于BP神经网络正反馈运算思想

韩莎莎(福建工程学院管理学院，福建福州350118)



建筑工程投标方案比选方法研究——基于BP神经网络正反馈运算思想

韩莎莎
(福建工程学院管理学院，福建福州350118)

摘要:建设项目的投标阶段，影响投标方案的因素多、受外界影响大，为此很难找出一种准确、便捷的方案比选手段。应用BP神经网络正反馈运算理论进行三种实例投标方案比选，得出最佳投标方案，阐述一种既便捷又精确的方法来进行投标方案比选。该方法不仅具有比选方案的基本功能，还具有风险预估的优势。

关键词:方案比选; BP神经网络;风险预估

在投标阶段，如何能够在众多投标方案中比选出最佳方案，且该方案风险预估能力最强显得尤其重要。

在参加投标时，施工单位必须做好充分的预测，在保证自己风险可控、利润最高的前提下，投出有利于自己中标的价格。

本文引入BP神经网络的正反馈运算思想进行投标方案选优和风险预估。在项目的投标阶段，存在着许多不确定因素，而这些不确定因素对投标阶段的方案比选起着不可忽视的作用，也是进行风险预估的对象。

1　BP神经网络进行投标阶段预测的应用背景

造价的不确定因素往往都要进行人为量化，量化值的大小又会受到造价人员主观、经验的影响，从而造成投标报价预测准确性不高、风险控制不好。BP神经网络通过输入层与输出层之间的正反馈运算，对输入值与计算输出值进行比较，当造价人员发现风险临界值与输入值接近时，则会得到一个预警，即该最优方案风险预留空间不足，需要对投标方案进行优化。由于BP神经网络的中间层的多少和运算参数均可以根据项目实际情况进行调整，所以该比选方法具有一定的实用价值。

2　引入BP神经网络的正反馈运算

2.1BP神经网络输入层、中间层以及输出层的确定

BP神经网络的正反馈运算原理［1－2］:按照BP神经网络的正向计算原理确定出输入层—中间层—输出层，假设输入变量为确定值，先通过中间层的计算推导，从而得出输出层的初步比选结果;然后，按照BP神经网络的误差反向计算原理［3］，把通过正向计算所得出的初步比选结果作为一个大前提，假定这个大前提是成立的，通过反向计算得出原先确定的输入层变量的取值范围。通过BP神经网络理论的运用，可以在已知输入变量变化的情况下快速估算出各种组合的期望值大小，最终选择出最佳方案。运用该模型进行预测不仅可预测出哪个方案可行，而且还能预测出当其中某一输入变量发生变化的条件下，该变量的变化区间与最终比选结果的关系。因此，本文在通过BP神经网络正向计算得出初步比选结果的前提下，再通过单因素敏感性分析理论进行反算，最终可确定拟选方案最优及风险范围值。

首先，根据已知的造价数据及相关的工程特点，构建BP神经网络的输入层、中间层以及输出层。确定输入层变量:这里把材料费、人工及机械费、利润等造价数据作为输入变量。确定中间层即运算层变量:根据相关项目的特点，将投标方案中人、材、机的各种组合作为运算层变量(本文以决策树作为运算层变量)。其中第一个隐藏层的输出作为下一个隐藏层的输入。计算输出层变量:通过中间层方法推算最终得出的数据即为输出层变量，这里将计算出的投标单位的相应的报价方案作为输出变量。

2.2模型的具体应用

实际案例:某具有相应资质的承包商经公司经营部研究决定参与某建设工程项目的投标。经造价工程师估算，该工程估算成本为1 800万元，其中材料费占60%，人工费及机械费占25%。经研究有高、中、低三个报价方案，其利润率分别为10%，7%，4%。根据过去类似工程的投标经验，相应的中标概率分别为0.4，0.6，0.8，投标的费用为6万元。由于满足固定总价合同的条件，故该工程业主单位在招标文件中明确规定采用固定总价合同。据估计，在施工过程中人工费及机械费可能平均上涨3%，材料费可能平均上涨4%。人工费及机械费、材料费均不涨发生概率为0.5;人工费及机械费上涨、材料费不涨发生概率为0.2;人工费及机械费不涨、材料费上涨发生概率为0.2;人工费及机械费、材料费均上涨发生概率为0.1［4］。根据案例背景，运用BP神经网络进行正反馈运算，选择一种最有利的报价方案。

根据已知的造价数据，输入变量——即在人工费及机械费、材料费是否上涨及投标报价时利润高低选择不同的情况下，分别计算出各投标方案的利润，也就是根据BP神经网络的原理按照预测模型正向计算出各投标方案的利润。

2.2.1BP神经网络的正向计算

根据预估数据，计算出各种情况组合下的利润值，计算结果如表1所示。

同理，根据预估数据，计算出各种情况组合下的利润及概率统计结果，计算结果如表2所示。

表1　各投标方案利润计算表Tab.1 The profit calculation of bidding schemes

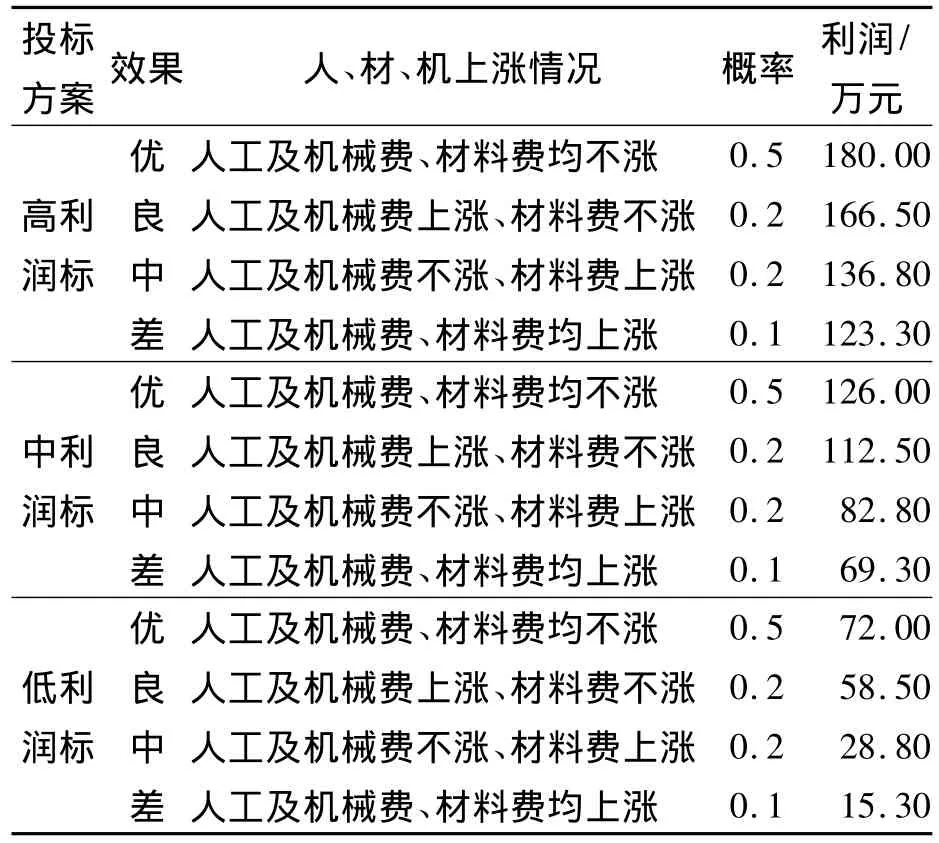
表2　各投标方案利润及概率统计表Tab.2　The profit calculation of bidding schemes and probability statistics

通过表2各投标方案利润及概率值绘制出决策树，如图1所示。

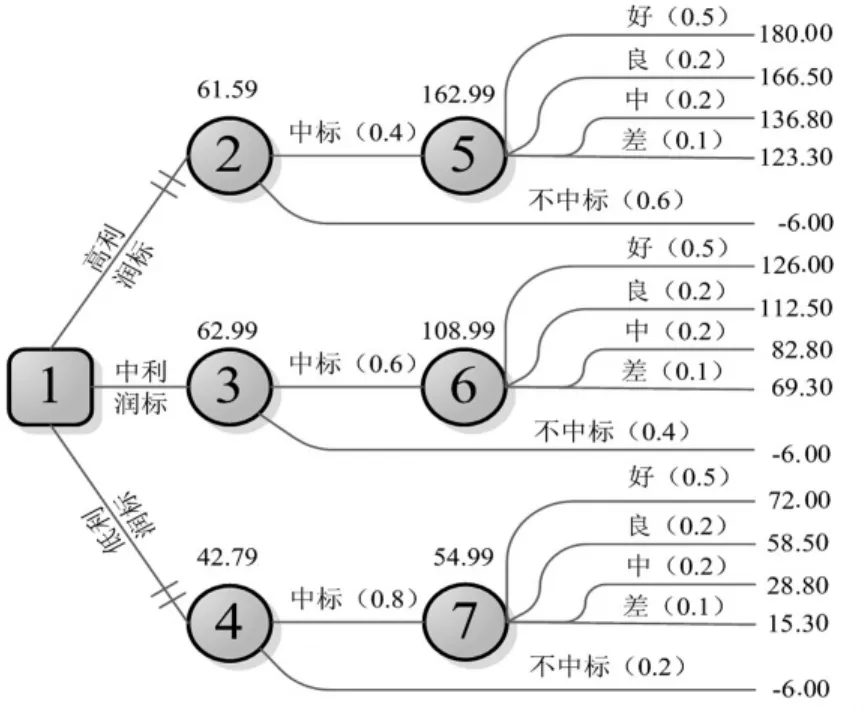
图1　投标方案比选决策树Fig.1　The decision-making tree for bidding schemes comparison

根据图1的各种组合发生概率情况，按照统计学原理计算出各机会点的期望值(将期望值标在决策树图中各机会点的上方)。

各机会点期望值的计算过程如下:

通过比较各机会点期望值大小，得出利润期望值最大的机会点是③，所以应选择按照中等利润投标。此时投标报价应为1 800×(1 +7%) = 1 926.00万元。

2.2.2BP神经网络的反向计算

通过输出层结果(即投中利润标利润期望值最大)反向计算，得出输入层的某一变量(材料上涨率)的取值范围，最终确定满足该结论正确性的风险大小。

这里假设正向计算结果正确，即按照中等利润投标方案进行投标。

假设材料费上涨率为x，其他输入层变量保持不变，即可以得到此时材料费上涨时各投标方案的利润，计算结果如表3所示。

表3　设定条件下各投标方案利润计算表Tab.3 The profit calculation of 3 bidding schemes

通过表3各投标方案利润及概率值绘制出决策树，如图2所示。

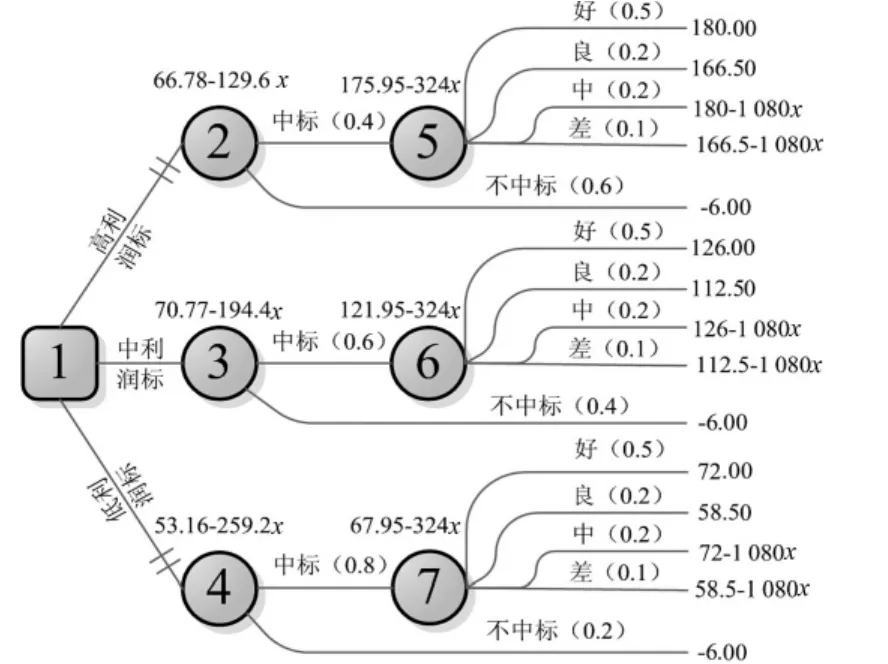
图2　设定条件下投标方案比选决策树Fig.2 The decision-making tree for bidding schemes comparison under set conditions

因为假设投中利润标为最佳方案(即正算结果正确)，此时机会点③的利润期望值最大。

所以可以得到

通过不等式计算，得－0.27≤x≤0.06根据工程实际情况材料费的上涨是必然趋势，所以材料费的上涨率x不可能为负值，经修正后的材料上涨率x的取值范围应该为0≤x≤0.06，即材料费涨幅极限为6%。

通过BP神经网络反馈计算理论得出风险预估范围为0～6%，而相对于估计的材料上涨率4%而言，风险预留空间不大，抗风险能力一般。

3　BP神经网络正反馈运算的检验及结论

3.1BP神经网络正反馈运算的检验

把材料费上涨的临界值6%分别带入机会点②、③、④计算，便可以得到:

通过计算比较，可以得出点③的期望利润值最大，所以仍选中价投标，即通过BP神经网络正反算计算，所得出的结果一致。

3.2结论

综上所述，材料费上涨的临界值为6%，当材料费上涨的百分比≤6%时，该项目投中利润标就可以获得最大利润，而当材料费上涨的百分比＞6%时，该项目投中利润标不再是最佳方案。这样，便通过BP神经网络的正反向运算不仅在各种投标方案中比选出最优投标方案，而且对于影响该结论正确性的影响因素变化区间进行界定。即，按照算出的这个临界值6%，快速比较出预留材料费上涨的空间有多大。这样便达到了运用BP神经网络正反算思想，快速进行投标时多方案比选及准确界定影响因素允许变化区间的目的，最终实现投标风险提前预估。

参考文献:

［1］董升伟.基于改进BP神经网络的轨道交通短时客流预测方法研究［D］.北京:北京交通大学，2013.

［2］崔东文.多隐层BP神经网络模型在径流预测中的应用［J］.水文，2013，33(1) :68－73.

［3］方一博，金涛，屈世显.非对称反馈神经网络中亚稳态的位置与稳定性［J］.陕西师范大学学报:自然科学版，2013，41(5) :46－49.

［4］全国造价工程师职业资格考试培训教材编审委员会.建设工程造价案例分析［M］.北京:中国城市出版社，2014: 153－156.

(责任编辑:肖锡湘)

BP neural network positive feedback computation-based comparison of construction project bidding

Han Shasha
(School of Management，Fujian University of Technology，Fuzhou 350118，China)

Abstract:Multiple factors may influence the bidding scheme at the bidding stage of the construction project，which makes it difficult to determine an accurate and convenient bidding comparison method.The best bidding scheme of three real/practical bidding alternatives was determined via neural network positive feedback back propagation (BP) computation.An accurate and convenient comparison method of bidding schemes was discussed.The results indicate that the method not only has comparative function，but also has the advantage of risk estimates.

Keywords:scheme comparison; back propagation (BP) neural network; risk estimates

doi:10.3969/j.issn.1672－4348.2015.01.018

作者简介:韩莎莎(1983－)，女(汉)，福建福州人，讲师，硕士，研究方向:管理科学与工程、工程造价。

基金项目:福建工程学院科研发展基金青年项目(GY－Z13007)

收稿日期:2014－10－12

中图分类号:F224

文献标志码:A

文章编号:1672－4348(2015) 01－090－04