调频连续波合成孔径雷达回波建模与信号分析

蔡永俊　张祥坤　姜景山

(1.中国科学院微波遥感技术重点实验室 空间科学与应用研究中心,北京 100190;

2.中国科学院大学,北京 100049)



调频连续波合成孔径雷达回波建模与信号分析

蔡永俊1,2张祥坤1姜景山1

(1.中国科学院微波遥感技术重点实验室 空间科学与应用研究中心,北京 100190;

2.中国科学院大学,北京 100049)

摘要从调频连续波合成孔径雷达(Frequency Modulated Continuous Wave Synthetic Aperture Radar, FMCW SAR)回波信号表达式出发,首先深入分析FMCW SAR回波信号特点,得到了FMCW SAR准确信号模型与瞬时频谱,并应用于Dechirp接收,得到Dechirp接收信号的等效模型;其次将FMCW SAR信号模型与传统脉冲SAR接收信号模型对比,揭示出FMCW SAR脉内雷达的连续运动对回波信号的影响;最后定量地分析其对图像重建的影响程度,继而揭示出在FMCW SAR中“停走停”假设能否被忽略．仿真结果验证了本文分析的有效性和准确性．

关键词线性调频连续波;合成孔径雷达;Dechirp;回波建模;“停走停”

联系人： 蔡永俊 E-mail: caiyongjun11@mails.ucas.ac.cn

引言

调频连续波(Frequency Modulated Continuous Wave, FMCW)合成孔径雷达(Synthetic Aperture Radar, SAR)具有体积小、重量轻、成本低和分辨率高等特点,近年来在军民用领域中均受到了越来越广泛的关注．FMCW技术自雷达问世之初就得到了迅速发展,并成功应用于机载雷达高度计[1]等领域,但后来由于雷达作用距离越来越远,收发隔离问题严重制约了其发展和应用．直到20世纪八九十年代,由于以下原因又得到了雷达界的重视并得到迅速发展:1)连续波雷达时宽大,峰值功率低,使得雷达发射机很容易利用固态器件实现;2)随着数字信号处理技术发展,雷达的距离可以很方便地利用快速傅里叶变换得到;3)连续波雷达发射信号具有很大的时宽带宽积,很难被传统侦察机截获,具有很好的低截获概率前景．

将FMCW技术与SAR相结合,使得这种新体制的SAR不仅具有FMCW雷达体积小、重量轻、造价低和抗干扰能力强等特点,同时又具有传统SAR的高分辨率的特点,非常适合精确制导武器和无人机等小型平台,成为SAR小型化发展的重要方向,也是SAR向更大范围应用的迫切需求[2-6]．对FMCW SAR回波模型的分析和研究对于理解其工作原理、观测几何和成像具有重要意义

由于FMCW SAR发射大时宽信号,信号持续时长一般为1～10 ms,而在脉冲SAR中该时长一般在微秒量级,所以对于FMCW SAR,在信号发射期间雷达的连续运动能否被忽略及“停走停”假设是否有效是该体制下首要考虑的问题,决定着现有常用的SAR成像算法能否直接应用于FMCW SAR,因为目前常用的SAR成像算法都是基于“停走停”假设推导出的[7]．因此,需要对一般情形下的雷达回波信号模型进行分析,区分与脉冲体制下雷达回波信号模型之间的差异,这对更好地理解FMCW SAR工作原理和回波信号具有重要理论意义,并为成像提供了重要依据．

本文直接从回波信号表达式出发,深入分析了FMCW SAR回波信号特点,推导出一般情况下的准确回波模型,得到准确的回波信号瞬时频谱,通过对回波模型进行等效近似然后应用于去调频(Dechirp)接收体制,最终得到Dechirp后的信号模型;基于该模型又深入分析了由于脉内雷达的连续运动对方位信号所产生的影响,定义了判定“停走停”假设是否成立的判决因子,由此得出在FMCW SAR中该假设不成立,并且得出由于雷达的连续运动在Dechirp距离频域所产生的最大位置偏差等于方位多普勒带宽．

1Dechirp原理

由于FMCW SAR一般采用Dechirp方式接收回波信号,Dechirp原理是将接收信号与发射信号或发射信号的延迟信号进行共轭相乘[8],由于FMCW SAR系统回波延迟一般很短且远小于发射信号时宽,所以常采用发射信号作为参考信号．经过Dechirp后,接收信号的相位变为

(1)

式中: f0为发射信号中心频率; k为其调频率; τ为目标回波延迟．将接收信号相位对距离时间t求导,可得到距离频率为

(2)

由式(2)可知,Dechirp将所有目标的回波信号变为一个单频的信号,频率瞬时值与信号回波延时有关．其过程如图1所示．由此可见,Dechirp使得信号带宽大大降低,从而可以降低对系统A/D采样模块的要求,最终能减轻系统重量和节约系统成本．

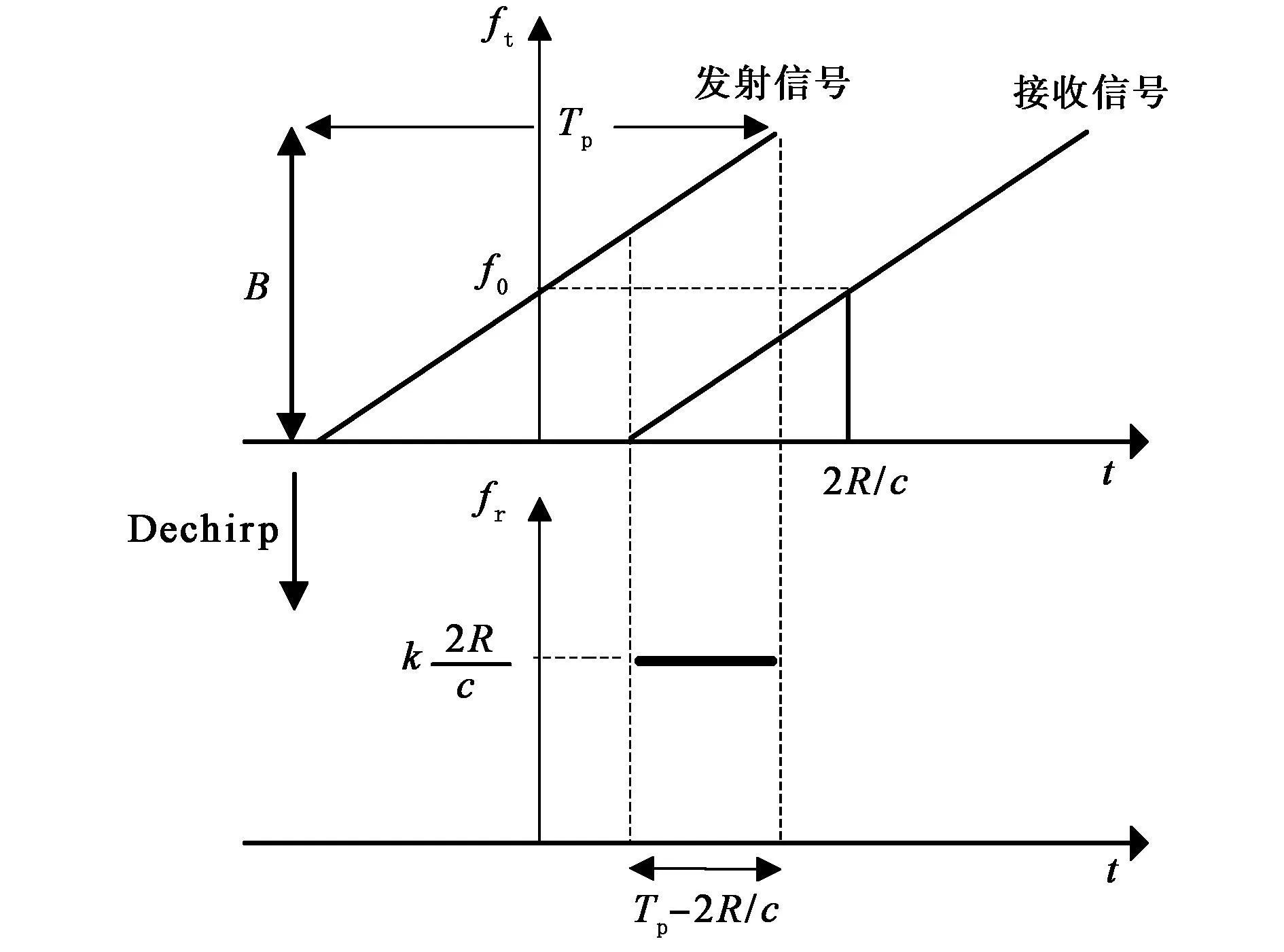
图1　发射/接收信号时频关系与去调频原理

2FMCWSAR回波信号建模

2.1　一般情况下回波信号模型

下文分析雷达的连续运动对回波信号的影响．

由于FMCWSAR发射信号时长较大,所以对于一个脉冲周期内的信号回波延迟是变化的[9-10],与某脉冲发射期间内雷达至某点目标的瞬时斜距有关,该瞬时斜距可以表示为

(3)

对式(3)在距离时间t=0处进行泰勒级数展开,由于在极短的脉冲持续时间Tp内,可忽略其二次及更高次项的影响,展开后瞬时斜距可表示为

(4)

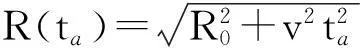
=τa+β t．

(5)

式中: τa=2R(ta)/c为在方位时刻ta的目标回波延时; β=2v2ta/cR(ta)为时延关于距离时间的变化量．

得到FMCWSAR回波信号模型为

(6)

式(6)为一般情况下回波信号相位的准确表达式,没有基于“停走停”假设,若令β=0,式(6)可简化为

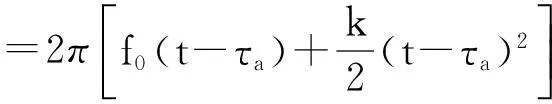
(7)

式(7)即为“停走停”假设下的目标回波表达式,没有考虑在脉冲发射期间雷达与目标瞬时斜距的变化所引起的回波时延的改变．

为了分析一般情况下回波信号的时频特性,将式(6)对距离时间t求导,得到

f=(f0-kβτa)(1-β)+(1-β)2k(t-τa)

=f0-βf0-kβτa+kβ2τa+(1-β)2k(t-τa)

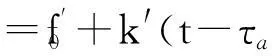
(8)

偏移,同样,接收信号的调频率和发射信号调频率也不同．所以,对于FMCWSAR,接收信号的时频特性并非是发射信号时频特性的简单延迟．FMCWSAR接收信号时频特性如图2所示．

说明:　a:发射信号的延迟信号曲线; 　b:一般情形下回波信号曲线图2　FMCW SAR发射/接收信号时频特性(便于观察已做夸大处理)

2.2　回波仿真

通过Matlab仿真FMCWSAR回波,进行短时傅里叶变换分析其时频特性,仿真参数如表1所示，结果如图3所示．图3中，曲线a为发射信号瞬时频谱,曲线b为“停走停”假设下的回波瞬时频谱,曲线d为一般情况下回波瞬时频谱．比较曲线b与d可知,一般情况下回波信号调频率相比于发射信号调频率是变化的;其次若无中心频率的变化,一般情况下回波信号频谱应为曲线c,由于曲线c与d之间存在某固定频率的差别,由此可知,一般情况下回波信号的中心频率也发生了改变,与上文分析一致．

表1　回波仿真参数(便于观察,已做夸大处理)

图4为仿真的回波信号频谱幅度图．如图所示,一般情况下的回波信号带宽相比“停走停”假设下信号带宽有所减小,是由于回波信号调频率发生了改变,所以仿真结果与分析一致．同时如图所示,一般情况下中心频率也发生了改变,验证了理论分析的正确性．

说明: a:发射信号瞬时频谱曲线; b:“停走停”假设下的回波瞬时频谱曲线; c:一般情况下回波信号频谱曲线; d:一般情况下回波瞬时频谱曲线图3　FMCW SAR模拟回波的瞬时频谱

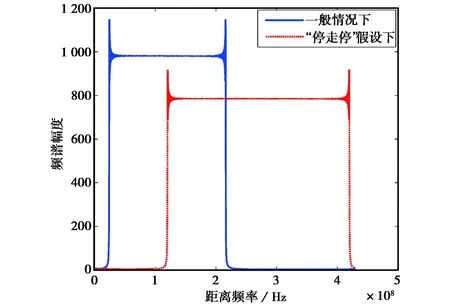
图4　接收信号频谱幅度图

2.3　模型的等效近似

下文定量分析这种脉冲发射期间雷达的连续运动对接收信号所产生影响的程度．

由2.1节可知,

(9)

式中:θ为方位时刻ta处的斜视角;λ为发射信号波长;fd为方位时刻ta处的多普勒频率．由式(9)可知,β为方位时刻ta处多普勒频率与发射信号载频的比值,将其代入式(8)可得

f=f0-βf0-kβτa+kβ2τa+(1-β)2k(t-τa)

(10)

由于fd一般在102量级上,而f0一般在109量级以上,所以fd/f0通常非常小,可以近似为0,因此式(10)可以简化为

=f0+fd-kτa+kt=f0+fd+k(t-τa).

(11)

将式(11)与式(7)相比较可知,由于脉冲发射期间雷达的连续运动对回波信号造成的影响可以近似地认为在信号中心频率处产生了一个频率偏移,偏移值为信号发射时刻方位多普勒频率,称之为脉内多普勒偏移．进行等效近似后,接收信号的时频关系如图5所示．

说明:　 a: 发射信号的时延信号的时频关系;　 b: 等效近似的回波信号的时频关系图5　发射/接收信号时频特性

接收信号的表达式(以复数表示)可以表示为

(12)

式中:τa=2R(ta)/c为ta时刻回波时延;A为回波信号的幅度;第一个相位项为Dechirp之后距离向的一次相位;第二个相位项是方位聚焦所需的相位,包含了在合成孔径时间内方位向信号的相干性;第三个相位项为剩余视频相位,是经Dechirp后产生的．

2.4　Dechirp接收信号模型

由式(12)第一个相位可知,该相位为距离向信号仅存的一次相位,由于在时域存在一次相位变换到频域就为sinc型的函数,峰值位置位于一次相位的频率处,因此将式(12)对距离时间t作傅里叶变换即可完成距离压缩,得到sinc型的窄脉冲为

s′(t)=ATpsinc{Tp[fr-(kτa-fd)]}

(13)

式(13)为一般情况下即考虑脉冲发射期间雷达的运动时基于Dechirp的回波信号距离压缩完后的近似准确表达式,其中,Tp为脉冲持续长度．而当采用“停走停”假设时,回波信号距离压缩完后,信号的表达式为

(14)

通过比较式(13)与式(14),一般情况下的Dec-hirp回波信号距离压缩后相比于采用“停走停”假设回波距离压缩后在距离频域产生了一个位置偏差,偏差大小为fd,恰好等于一般情况下回波信号的中心频率偏移值．因此可以得知,由于在脉冲发射期间雷达的连续运动导致的雷达与目标瞬时斜距的改变对Dechirp回波模型的影响可以近似地认为使得回波信号距离压缩后在距离频域产生了一个位置偏差,偏差大小为在脉冲发射之时的瞬时多普勒频率值．那么该位置偏差对成像的影响能否被忽略是该体制首要考虑的问题,决定了“停走停”假设能不能应用于FMCW SAR,从而可以简化成像过程．下文主要分析这个位置偏差对成像的影响程度．

3“停走停”假设有效性判定

3.1　判决因子

关于斜距偏移是否能被忽略,需要将频率偏移量fd转换成距离大小并将其与距离分辨率作比较,所以定义参数

(15)

用以衡量由于雷达的连续运动在距离向所产生的偏移的影响程度．式中:ρr为距离分辨率;fd为脉冲发射时刻的瞬时多普勒,表达式为

(16)

θ为瞬时斜视角．所以,对于一个方位孔径范围,回波信号由于雷达的连续运动所产生的最大距离偏移量为

(17)

式中,θmax与θmin分别为雷达天线波束范围内的最大与最小斜视角．由于方位多普勒带宽具有以下形式:

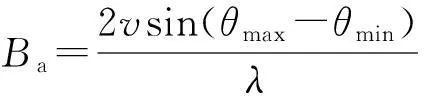
(18)

所以,

Δfmax=Ba．

(19)

即非“停走停”假设下,不同方位位置的回波信号在距离频域产生的最大位置偏差等于方位多普勒带宽．所以,式(15)的最大值为

(20)

对于FMCW SAR,其距离分辨率为(以发射信号作为参考信号)

(21)

式中,B=kTp为发射信号带宽．可以看到,距离分辨率与距离向回波延迟及目标与雷达的距离有关,距离越远,分辨率越低,但对于FMCW SAR应用,回波延迟对分辨率的影响程度很弱,为了便于推导,简化分辨率的表达式并代入式(20),可得

(22)

令μ=Tp/IPR=Tp·FPR为发射脉冲占空比,其中IPR,FPR分别为脉冲重复间隔与脉冲重复频率．式 (22)可以改写为

(23)

式(23)将K的表达式与雷达系统参数联系了起来,即“停走停”假设成立与否,取决于式(23)中的雷达系统参数,这给“停走停”假设的判决提供了形象直观的工具．根据“停走停”假设成立的条件,K必须满足[8]

Kmax≪1．

(24)

对于脉冲式SAR,发射脉冲时间宽度Tp一般为微秒量级,假设为10 μs,FPR假设为500 Hz,则占空比μ=0.005≪1,而对于SAR系统,FPR取值一般稍大于多普勒带宽Ba,所以满足Kmax≪1,“停走停”假设成立．然而对于FMCW SAR,雷达连续不断地发射脉冲,信号占空比μ=1,判决因子K通常约等于1,不满足“停走停”假设成立条件式(24),所以对于FMCW SAR,脉内雷达运动导致的不同方位信号在距离向上产生的偏移不能被忽略．

3.2　点目标回波仿真

下面通过Matlab仿真点目标的回波,在距离向查看由于脉内多普勒偏移导致的附加距离徙动的影响程度．仿真参数如表2所示．

表2　点目标回波仿真参数

图6和图7显示了由于脉内雷达的连续运动在距离向导致的附加偏移的最大程度,即在非“停走停”假设下不同方位回波在距离向上引起的附加偏移的最大程度．图6为FPR为1 000Hz时的最大附加偏移,由式(15)知,最大偏移量为K·ρr,又由式(23)知,当FPR=1 000Hz时,Kmax约为1,所以最大偏移量约等于距离分辨率;当FPR=2 000Hz时,Kmax约为0.5,即最大偏移量应约为距离分辨率的一半．从图6和图7的仿真结果可看到,后者的偏移程度约为前者的一半．图8为FPR=1 000Hz(K=1)时“停走停”假设下的距离压缩二维结果,可发现,当使用“停走停”假设分析时,脉冲起始处的回波与脉冲结束处的回波存在一个距离单元的徙动,也即徙动达到一个分辨单元,由上文分析这是不能被忽略的,必须加以校正．所以,以上仿真结果很好地验证了本文理论分析的准确性．

图6　FPR=1 000 Hz时脉内雷达连续运动引起的最大附加距离徙动

图7　FPR=2 000 Hz时脉内雷达连续运动引起的最大附加距离徙动

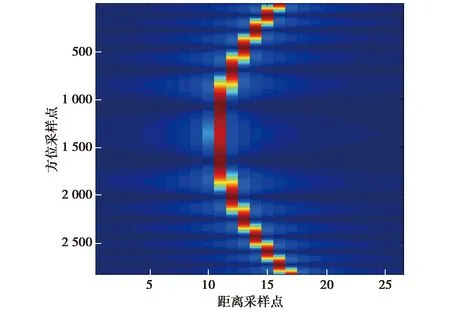
图8　FPR=1 000 Hz时距离压缩二维结果

4结论

本文系统而全面地分析了FMCWSAR回波信号模型,得到一般情形下回波信号模型及其瞬时频谱,揭示了其与“停走停”假设下的回波模型的区别,对理解FMCWSAR信号形式和工作原理具有重要意义,并通过仿真结果验证了分析的准确性;然后对其等效近似应用于Dechirp接收体制,得到Dechirp信号的近似模型,深入分析由于脉内雷达运动对回波信号的调制过程及对不同方位回波信号的影响,为FMCWSAR成像提供了重要依据;基于此等效模型,分析了多普勒偏移是否能被忽略,得到最大距离偏差等于方位多普勒带宽的结论,并通过设置不同参数仿真了点目标回波,仿真结果均验证了本文分析的有效性和准确性．

参考文献

[1]GRIFFITHSHD.Syntheticapertureprocessingforfull-derampradaraltimeters[J].ElectronicsLetters, 1988, 24(7): 371-373.

[2]WITJJMDE,HOOGEBOOMP.PerformanceanalysisofahighresolutionairborneFM-CWsyntheticapertureradar[C]//ProcIRS.Dresden, 2003.

[3]DUERSCHMI.BYUMicro-SAR:AVerySmallLow-powerLFM-CWSyntheticApertureRadar[D].Provo:BrighamYoungUniversity, 2004.

[4]刘闯, 洪香茹, 张涛. 小型SAR系统设计[J]. 火控雷达技术, 2012, 41(1): 1-5.

LIUChuang,HONGXiangru,ZHANGTao.Designofmini-SARsystem[J].FireControlRadarTechnology, 2012, 41(1): 1-5. (inChinese)

[5]葛亦斌, 金亚秋, 王海鹏. 一种实验室合成孔径雷达对目标散射的成像试验[J]. 电波科学学报, 2013, 28(3): 430-437.

GEYibin,JINYaqiu,WANGHaiping.LaboratoryexperimentsfortargetscatteringandimagingusingfullypolarimetricFMCWradarsystem[J].ChineseJournalofRadioScience, 2013, 28(3): 430-437. (inChinese)

[6]高许岗, 雍延梅. 无人机载微型SAR系统设计与实现[J]. 雷达科学与技术, 2014, 12(1): 35-38.

GAOXugang,YONGYanmei.DesignandrealizationofUAVhighresolutionminiatureSAR[J].RadarScienceandTechnology, 2014, 12(1): 35-38. (inChinese)

[7]张军, 毛二可.线性调频连续波SAR成像处理研究[J].现代雷达, 2005, 27(4): 42-45.

ZHANGJun,MAOErke.AstudyonLFMCWsignalprocessing[J].ModernRadar, 2005, 27(4): 42-45. (inChinese)

[8]METAA.SignalProcessingofFMCWSyntheticApertureRadarData[D].Delft:DelftUniversityofTechnology, 2006.

[9]LIUY,DENGY,WANGR.BistaticFMCWSARsignalmodelandimagingapproach[J].IEEETransactionsonAerospaceandElectronicSystems,2014, 49(3): 2017-2028.

[10]NAVNEETS,ROYA,BHATTACHARYAC.High-resolutionSARimagegenerationbysubapertureprocessingofFMCWradarsignal[J].IEEEGeoscienceandRemoteSensingLetters, 2014, 11(11): 1866-1870.

蔡永俊(1989-),男,江苏人,在读博士研究生,研究方向为合成孔径雷达信号处理与系统研究、全极化合成孔径雷达信息处理等．

张祥坤(1972-),男,山东人,研究员,研究方向为合成孔径雷达信号处理与系统研究、微波遥感理论与技术等．

姜景山(1936-),男,吉林人,研究员,博士生导师,中国工程院院士,国际欧亚科学院院士,现为中国科学院空间科学与应用研究中心学术委员会主任,从事微波遥感理论与技术研究40年,在机载遥感信息实时传输领域具有开创性贡献,先后有多项科研成果获国家级、部级、中科院院级奖励．

李磊, 吴振森, 林乐科, 等. 14.1 GHz海上微波超视距传播衰落斜率特性研究[J]. 电波科学学报,2015,30(6):1164-1169. doi: 10.13443/j.cjors. 2015010902

LI Lei, WU Zhensen, LIN Leke, et al.The fade slope of microwave trans-horizon propagation on oversea at 14.1 GHz[J]. Chinese Journal of Radio Science,2015,30(6):1164-1169. (in Chinese). doi: 10.13443/j.cjors. 2015010902

Echo modeling and signal analysis of frequency modulated

continuous wave synthetic aperture radar

CAI Yongjun1,2ZHANG Xiangkun1JIANG Jingshan1

(1.Keylaboratoryofmicrowaveremotesensing,ChineseAcademyofSciences,

CenterforSpaceScienceandAppliedResearch,Beijing100190,China;

2.UniversityofChineseAcademyofSciences,Beijing100049,China)

AbstractThis paper starts from the expression of frequency modulated continuous wave synthetic aperture radar (FMCW SAR) echo signal. Firstly, the characteristic of FMCW SAR echo isanalyzed, and then the accurate signal model and instantaneous spectrum are obtained. Based on these, the equivalent Dechirp signal model is obtained. Secondly, the signal model of FMCW SAR and pulse SAR are compared, and then the influence on the echo owing to the successive motion within a pulse sweep is revealed, based on which, the impact on the image reconstruction is quantitatively analyzed. At last, whether the “stop-go-stop” approximation is valid in FMCW SAR is revealed. The simulation results verify the effectiveness and exactness of the above analysi.

Key wordsfrequency modulated continuous wave; synthetic aperture radar; Dechirp; echo modeling; “stop-go-stop”

作者简介

收稿日期：2014-12-09

中图分类号TN958

文献标志码A

文章编号1005-0388(2015)06-1157-07