Snel失速模型在旋翼非线性挥舞运动中的应用

刘 洁，陈 蕾，张 峰

(空军航空大学， 吉林 长春 130022)



Snel失速模型在旋翼非线性挥舞运动中的应用

刘 洁，陈 蕾，张 峰

(空军航空大学， 吉林 长春 130022)

首先通过对旋翼桨叶叶素的受力分析，建立了适用于大入流角和大挥舞角的非线性旋翼桨叶挥舞方程。为了使所建立的挥舞方程具有更好的通用性，首次将Snel失速模型应用于直升机旋翼失速状态下升力系数的确定问题，并通过对特定翼型进行仿真试验，验证了Snel失速模型在旋翼问题研究中的有效性。试验表明该模型具有很好的准确性，且由于该模型中不含任何试验参数，实用性强。

旋翼桨叶；挥舞运动；非线性；Snel失速模型

0 引言

直升机是由桨叶的运动来提供前进动力和升力的一种飞行器，由于它具有悬停、机动性强等突出特点，在军用和民用领域的应用越来越广泛[1]。直升机桨叶的运动包括旋转运动、挥舞运动、摆振运动和扭转运动，本文主要研究了刚性桨叶的挥舞运动。研究直升机旋翼桨叶的挥舞运动，最主要的就是建立桨叶的挥舞方程。目前大多数学者，如Leishman[3]和Johnson[4]等，都是基于小入流角、小挥舞角的假设前提，将挥舞方程进行线性近似化处理从而建立挥舞方程的。这种方法在小入流角和小挥舞角时能较为方便地解决工程问题，但在大角度时就不适用了。为了解决这一问题，本文首先对桨叶叶素进行分析，进而建立一种既适用于小角度又适用于大角度的非线性挥舞运动方程。

为了求解挥舞方程，首先需要确定挥舞方程中的升力系数和阻力系数。对于小前进比和小角度而言，升力系数可视为与迎角呈线性关系，阻力系数通过二阶多项式拟合得到[5]。但当大前进比和大迎角时，旋翼容易陷入失速状态，这种简单的近似关系不能准确地求出升力系数和阻力系数。为了解决这一问题， Barakos和Spentzos等利用CFD方法来计算失速状态下的升力系数和阻力系数[6-7]，这种方法计算精度较高，但需要耗费大量时间，不利于实时计算。为了得到一种既满足于精度又满足实时性要求的方法，Leishman、Beddoes和Crouse等人提出了Leishman-Beddoes模型[8-10]，Tran 、Pitot和Falchero等人提出了ONERA模型[11-13]，这两种模型都是基于静态条件下的试验数据而得出的半经验模型，能很好地解决升力系数和阻力系数的确定问题，但由于模型中均需要不同个数的经验参数，对模型的应用产生了一定的影响。为了找到一种更好的模型，本文将应用于弹性风力涡轮机的Snel失速模型应用到旋翼问题中，并采用Leishman提出的准静态失速模型解决阻力系数的问题。然后，通过仿真试验，验证Snel失速模型的有效性。

1 桨叶挥舞方程的建立

1.1 叶素受力分析

为了建立旋翼的挥舞方程，本文基于叶素法对桨叶进行分析。首先在方位角为φ处的桨叶某一站位处(r=y)选取桨叶微元dr(桨叶剖面如图1(a)所示)，并对所选取的叶素进行分析。

所选叶素的速度示意图如图1(a)所示，其中UT为桨盘平面内的速度分量，UP为垂直于桨盘平面的速度分量，UR为径向的速度分量，这三个速度的表达式为：

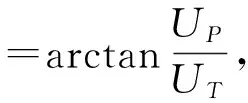
图1 叶素的受力分析图

1.2 挥舞方程的建立桨

桨叶的挥舞运动主要取决于相对于桨毂中心的惯性力矩和空气动力产生的力矩的关系，为了建立桨叶的挥舞运动方程，本文桨叶视为刚性桨叶。作用在叶素上的力主要有惯性力、离心力以及空气动力，具体如图1(b)所示。

由于φ=Ωt，则可将旋翼的挥舞方程写为：

利用式(3)，就可以计算出不同状态下，在不同方位角处的挥舞角。

2 Snel动态失速模型

由于升力系数Cl(α)和阻力系数Cd(α)均为迎角α的函数，在迎角比较小时，升力力系数与迎角可近似为线性关系，并采用二阶多项式拟合的方式来得到阻力系数与迎角的关系。随着迎角的增大，就会出现气流的分离和失速现象，这对旋翼升力的分布会产生比较大的影响，而升力系数与迎角的关系变得不规则，一般很难用简单的多项式来得到。

动态失速条件下的旋翼或桨叶的负载计算是一项非常具有挑战性的工作。目前，比较常用的方法有涡理论和Navier-Stokes数值计算，这些方法虽具有较好的准确性，但计算量较大，从而影响到实时性[14]。为了克服这一点，本文考虑建立一种易于解算又能保证精度的动态失速模型。

在旋翼的综合分析中，由于稳态下的升力系数Cl(steady)通过试验易于获得，所以常常基于此采用半经验模型。目前，已有很多半经验动态失速模型被用于飞行器研究之中，其中最常用的两个模型为：Beddoes-Leishman模型和ONERA 模型。Beddoes-Leishman模型重于分析从而简化计算的目的，主要利用一系列的常微分方程来计算升力系数；ONERA半经验模型用一个一阶和一个二阶的非线性微分方程来描述旋翼的不稳定行为，其中一阶线性微分方程描述了非粘性(附着流)空气动力学的部分，二阶微分方程描述了非线性粘滞效应。在这两种模型中往往包含一些参数，这些参数的确定通常都是基于特定翼型的动态或静态测量数据，这也给模型的应用带来了不便，为了解决这个问题，本文采用Snel模型[15]。

Snel模型是由H. Snel提出的[16-17]，目前应用于弹性风力涡轮机的失速效应分析中。该模型将升力系数与稳态下的升力系数之差写成两部分之和，一部分是描述力的频率响应ΔCl,1，另一部分是描述更高频率下的空气动力ΔCl,2。则升力系数可写为：

其中，ΔCl，1是采用一阶微分方程来得到，ΔCl，2是采用二阶的微分方程来得到[18]，具体如下：

根据Snel模型，C10的取值为：

其中，Δ=2πsin(α-αZ)-Cl(steady)，表示线性升力系数与稳态下的升力系数之间的差值，αZ为零升迎角。F1(φ)为一阶激励项，其取值为势流项与稳态项升力系数之差对时间常数的导数：

根据Truong VK.和H. Snel[18]的描述，可将C21写为：

C20的表达式为：

二阶激励项是关于势流项与稳态项升力系数之差的函数，即F2(φ)为：

应用上述模型就可以确定出升力系数(特别是失速条件下的)。

而阻力相对于升力较小，本文根据J.G. Leishman对不同迎角下的阻力系数近似表达式来获得不同迎角下的阻力系数：

其中，αS为失速迎角的临界值，a0、a1、a2的取值视不同翼型而定。

3 仿真试验

本文将桨叶视为是由沿径向不同站位处的一系列无限薄的截面组成，为了解决挥舞方程的积分问题，本文考虑将站位r0(利用桨叶半径处理后的无量纲量)处，将无限小的桨叶微元Δr作为研究对象。

3.1 研究对象

3.2 Snel失速模型的验证

本文在θ1c=2°，θ1s=-6°，μ=0.6(忽略反流区的影响)的条件下，取不同的θ0，采用Snel模型和B-L模型对挥舞方程进行求解，得出了挥舞角与方位角的变化关系，如图3所示。

由图2和图3可以看出，采用本文所提出的Snel模型得出的旋翼挥舞响应曲线，基本和采用经典的B-L模型得出的旋翼挥舞响应曲线相重合，这说明了Snel模型在处理直升机旋翼失速问题中具有很高的可信度，且Snel模型中无任何经验参数，这也使该模型具有更好的适用性。

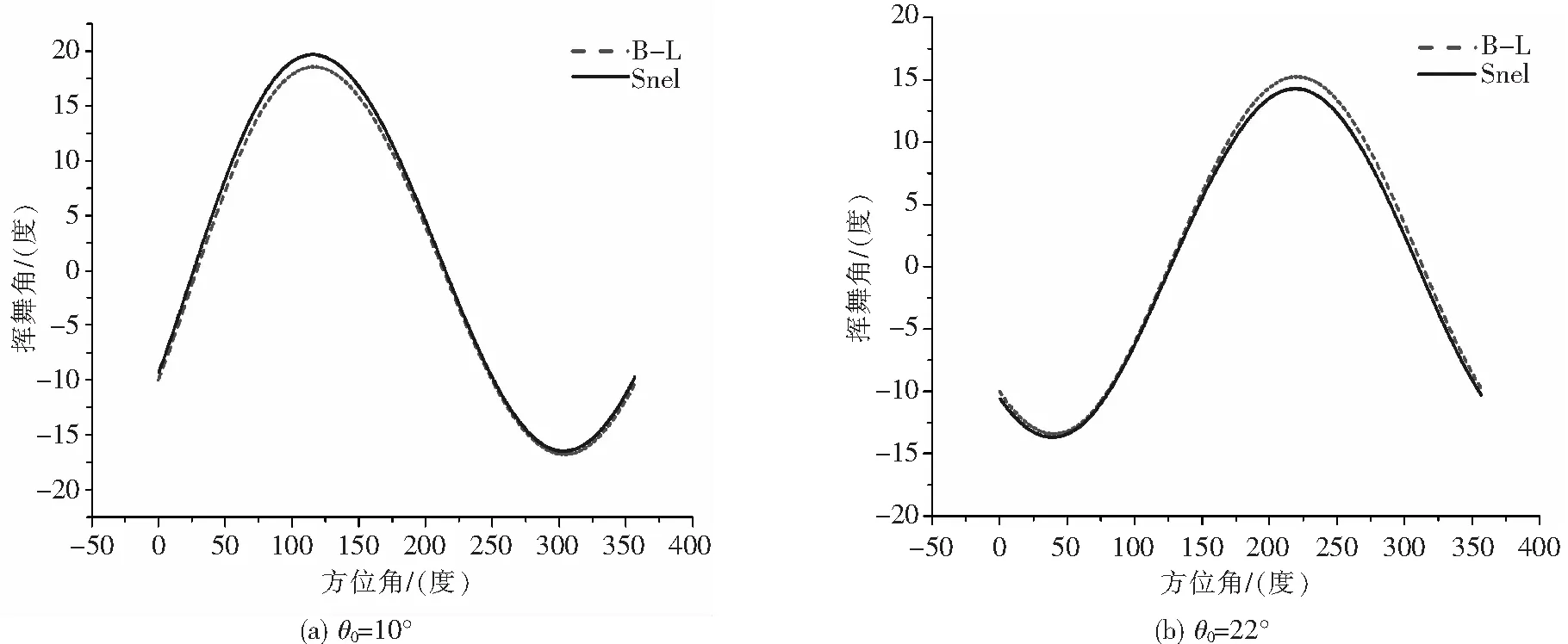
图2 挥舞角随方位角的变化关系

图3 挥舞角与方位角的变化关系

4 总结

本文通过对桨叶叶素进行分析，建立了既适用于大入流角和挥舞角又适用于小角度的挥舞方程，并首次将Snel动态失速模型应用到直升机领域，解决了动态失速条件下的升力系数的求取问题。为了验证Snel模型的有效性，本文将某机型上的OA212翼型作为试验对象，进行仿真验证，结果表明该模型具有很好的适用性和准确性。

[1] Babu J, Thomas B J. Helicopter Flapping Under Dynamic Stall. International Journal of Modern Engineering Research[J]. 2014, 4.

[2] Bramwell A R S, Done G, Balmford D[J]. Bramwell’s Helicopter Dynamics, 2001 (5).

[3] Leishman J G. Principle of HelicopterAerodynamics[M]. Cambridge University Press,1992.

[4] Johnson W. Helicopter Theory[M]. Princeton University Press,1975.

[5] Dreier M E. Introduction to Helicopter and Tiltrotor Simulation[R].American Institute of Aeronautics and Astronautics,2012.

[6] Snentzos A, Barakos G N, Badock K J, et al. CFD Study of Three-Dimensional Dynamic Stall of Various Planform Shapes[C]. 30th European Rotorcraft Forum, Marseilles, France, 2004:14-16.

[7] Barakos G, Drikakis D, Leschziner M A. Numerical Investigation of the Dynamic Stall Phenomenon Using Non-Linear Eddy-Viscosity Models[C].AIAA Paper 98-2740, 16th AIAA Applied Aerodynamics Conference, Albuquerque, NM, 1998:15-18.

[8] Leishman J G, Beddoes T S. A Generalized Method for Unsteady Airfoil Behavior and Dynamic Stall Using the Indicial Method[C]. 42nd Annual Forum of the American Helicopter Soc., Washington DC, 1986:2-5.

[9] Leishman J G, Beddoes T S. A Semi-Empirical Model for Dynamic Stall[J].Journal of the American Helicopter Soc, 1989,34 (3):3-17.

[10] Leishman J G, Crouse G L Jr. State-Space Model for Unsteady Airfoil Behavior and Dynamic Stall[R]. AIAA Paper No. 89-1319, April 1989.

[11] Tran C T, Pitot D. Semi-Empirical Model for the Dynamic Stall of Airfoils in View of the Application to the Calculation of the Responses of a Helicopter Blade in Forward Flight[J].Vertica, 1981,5 (1):35-53.

[12] Tran C T, Falchero D. Application of the ONERA Dynamic Stall Model to a Helicopter Rotor Blade in Forward Flight[C].7th European Rotorcraft Forum, Garmisch-Partenkirchen, 1981,Sept:22-25.

[13] Yeo H. Calculation of Rotor Performance and Loads Under Stalled Conditions[C]. American Helicopter Society 59th Annual Forum, Phoenix, AZ, May 2003.

[14] Floros M W, Gold N P, Johnson W. An Exploratory Aerodynamic Limits Test with Analytical Correlation[C]. American Helicopter Society 4th Decennial Specialist’s Conference on Aeromechanics, San Francisco, CA, January 2004.

[15] Holierhoek J G, Vaal J B de, Zuijlen A H van, et al. Comparing different dynamic stall models[J].Wind Energy, 2013(16):139-158.

[16] Montgomerie B. A dynamic stall model called SIMPLE[R]. Technical Report ECN-C-95-060, Netherlands Energy Research Foundation ECN, June 1995.

[17] Truong V K. A 2-D dynamic stall model based on a HOPF bifurcation[C]. 19th European Rotorcraft Forum Proceedings, C23, Cernobbio, Italy, 1993.

[18] Snel H. Heuristic modelling of dynamic stall characteristics[C]. European Wind Energy Conference, Dublin Castle, Ireland, 1997:429-433.

The Application of Snel Dynamic Stall Model in Nonlinear Flap Motion

LIU Jie, CHEN Lei, ZHANG Feng

(Aviation University of Air Force, Changchun 130022, China)

In this paper, the nonlinear flapping equation for the large inflow angles and flap angles was established by analyzing the aerodynamics of the blade elements. In order to get a more general flap equation, the Snel stall model was first applied to determine the lift coefficient of helicopter rotor. What’s more, a simulation experiment for specific airfoils was conducted to verify the effectiveness of the Snel stall model in field of the helicopter. The result showed that the model contains no parameters compared with other stall model, which was more convenient for practical application, and it also showed good accuracy and strong practicability.

rotor blade; flapping motion; nonlinear; Snel dynamic stall model

2015-07-01

吉林省科技发展计划项目(201403007ZG)。

刘 洁(1990-)，男，湖北英山人，硕士研究生，主要研究方向为飞行器仿真。

1673-1220(2015)03-001-04

V211.52

A