基于频率法和非线性静力求解法对短吊索抗弯刚度的识别

王进军　李万霞　何有为

(1.中交二航局六公司　武汉　430014;　2.湖北兴达路桥股份有限公司　咸宁　437100)

基于频率法和非线性静力求解法对短吊索抗弯刚度的识别

王进军1李万霞1何有为2

(1.中交二航局六公司武汉430014;2.湖北兴达路桥股份有限公司咸宁437100)

摘要吊索弯曲刚度与多种因素有关，是一个未知的参数，在工程实践中往往难以准确识别。文中选取了某悬索桥3 m长由直径为5 mm高强镀锌钢丝组成的吊索作为研究对象，采用频率法和非线性静力求解法分别推求短吊索的抗弯刚度，按修正后的抗弯刚度对吊索进行受力分析。结果表明，该悬索桥短吊索的球形转动装置可以取消，不仅可以降低工程成本，还便于日常养护。

关键词频率非线性短吊索刚度试件传感器测点

吊索弯曲刚度与其内部结构形式、钢丝间的粘结程度、结构的使用状态、振动形式等因素有关，是一个未知的参数。在工程实践中拉索的弯曲刚度往往难以准确识别[1]。目前，国内外常用的索力测定方法主要有压力传感器法、液压千斤顶法、振动频率法、磁通量法等几种[2]。振动频率法测试索力可考虑刚度影响，在索力已知的情况下，就可反推吊索刚度。

某悬索桥吊索采用73根直径5.0 mm高强镀锌钢丝组成，最短的吊索为2.813 m，由于桥面较窄，横风作用下横向变形较大，短吊索的刚度影响敏感。设计时为满足短吊索横向变形需要，桥跨中部17对较短的吊索上端设有球向转动装置。但该装置构造复杂，增加养护难度和影响耐久性。施工时增加了专题研究，通过短吊索的弯曲刚度的研究，精确计算短吊索的应力，对短吊索的安全性进行评价，研究是否可取消吊索球向转动装置。

研究取3 m长的吊索作为试件，重点研究短吊索的弯曲刚度的识别方法，采用频率法和非线性静力求解法分别推求抗弯刚度，并对2种方法进行对比分析。

1试验方案

1.1　试验试件及仪器

取3 m长吊索作为试件，试验装置示意见图1、图2，试验设备主要由吊杆及配套锚具试件、张拉台座、张拉千斤顶、压力传感器、应变传感器及数据采集系统，计算机、机电百分表、钢丝绳等组成。

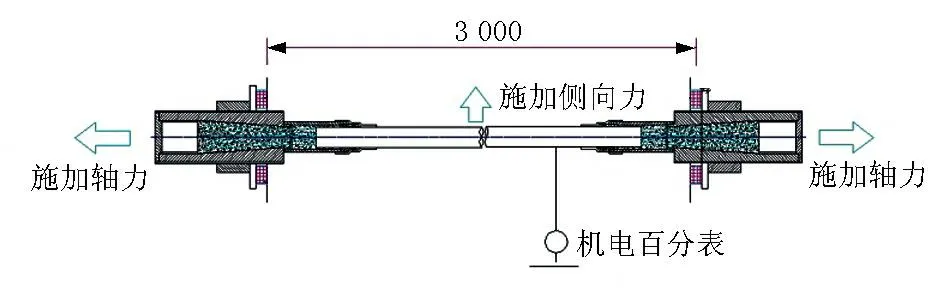
图1　试验装置示意

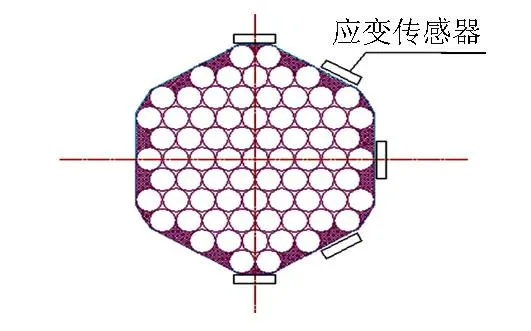
图2　吊杆截面

1.2　测点布置

(1) 应力测点。在吊杆张拉端压力传感器沿圆周方向布置4个压力盒，布置位置见图3，从4个压力盒和分别读取压力值，根据压力值计算端部弯矩和轴力。

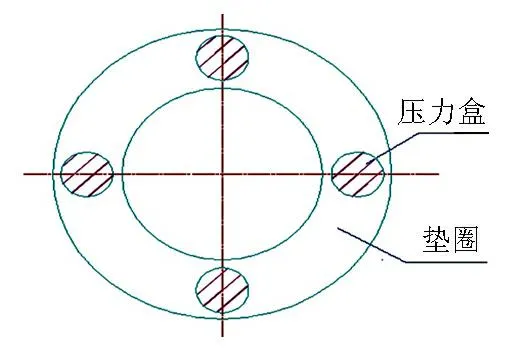
图3　压力盒布置位置示意

(2) 应变测点。在吊杆两端和L/2截面附近(测试时需准确量测测点布置位置)处布置测量断面，测量断面沿圆周方向布置5个测点，分别读取5个测点的应变值，通过应变推导截面的应力分布，验证截面是否满足平截面假定。

(3) 位移测点。在吊杆L/2、L/4和3L/4截面处布置挠度测点，测量以上断面处的吊杆体的位移，位移由机电百分表直接测量。

1.3　试验方案

试验通过2种途径分别测量吊杆的抗弯刚度：①频率法，给吊杆施加轴力，通过频率法识别抗弯刚度；②横向加载静力求解法，在吊杆跨中施加侧向力，通过吊杆力和变形测试结果推算抗弯刚度。

1.3.1频率法测抗弯刚度

(1) 在台座上安装吊杆，吊杆两端拧紧螺母，垫圈下安放压力传感器。

(2) 按4组工况进行加载，加载值分别取破断荷载的20%，30%，40%和60%，即160，320，480，640 kN。

(3) 对于每级荷载，在环境激励下利用加速度传感器拾取吊杆的随机振动信号，然后通过频域分析获取吊索的频谱图，据此识别出斜拉索的各阶振动固有频率。

(4) 通过理论分析(解析法与有限元法)与现场标定，获取吊杆索力与振动固有频率之间的对应关系。

(5) 根据实测的各阶频率及上述关系，识别吊索抗弯刚度。

1.3.2横向加载法测抗弯刚度

(1) 在台座上安装吊杆，吊杆两端拧紧螺母，垫圈下安放压力传感器。

(2) 按4组工况进行吊杆张拉加载，加载值分别取破断荷载的10%，20%，30%和40%，通过横向加载，使吊杆力控制到设计荷载的20%，30%，50%和80%，即160，320，480，640 kN。

(3) 首先精确测试初始垂度，对于每级荷载，分别根据百分表读取吊杆的挠度、吊杆测量截面的应变、压力盒读数，以及千斤顶油压表读数。

(4) 结合应变、挠度以及压力分布值推算吊杆的抗弯刚度。

2试验结果分析

2.1　分析理论

2.1.1频率法

(1) 基本原理。利用频率法测试索力是测试结构自振频率、分析其自振特性从而求出索力的方法。将索力动测仪的拾振器附着于吊杆, 拾取吊杆的振动信号, 经过滤波、放大、谱分析, 得到吊杆的自振频率, 然后根据索力与吊杆频率间的固有关系来确定索力。

应用结构动力学原理，建立吊杆的微分振动方程。

式中:EI为吊杆的弯曲刚度；x为沿吊杆轴向的坐标,m；y为吊杆的振幅,m;T为吊杆的索力,N;W为吊杆单位长重量,N/ m。其中第一项体现了抗弯刚度对吊杆振动的影响。

(2) 给对索力求频率。采用有限元法对吊杆进行自由振动分析, 可得如下特征方程。

式中：M为质量矩阵；K为刚度矩阵；ω为固有圆频率，Φ为振型。

对于某一给定的吊杆力T, 根据初应力刚度矩阵可进行静力求解获取索应力后得到。求解上述特征方程即可得到在T作用下斜拉索的各阶固有频率fi(i=1,2,…,n)，i为频率阶数；n为所考虑的最高阶频率的阶数。

(3) 索力、频率关系的数值拟合。利用解析法的实用公式初步估算吊杆力范围，在此范围内取多个吊杆力，求解出各个吊杆力作用下的频率，通过数值拟合确定吊杆力与频率的关系。

Ti=Ti(fi)

(4) 抗弯刚度识别。在合理范围内将抗弯刚度按0.05(EI)max的步长进行递增，对应每个抗弯刚度，可得出一族吊杆力与频率的关系曲线。根据实测各阶频率和假定的抗弯刚度推求吊杆力，将所得吊杆力与实测吊杆力进行对比来识别抗弯刚度。另外，由于索力是惟一的，因此不同频率数的实测索力应该一致，据此也可识别抗弯刚度。

2.1.2非线性静力求解法

(1) 基本原理。首先对吊杆进行侧向加载，使吊杆产生弯曲变形，吊杆两端边界条件通过端部测点应力测试识别，计入几何非线性，根据静力求解方法识别抗弯刚度。

(2) 弯矩刚度的有限元识别。在每级加载工况下，抗弯刚度按0.05(EI)max的步长进行递增，对应每个抗弯刚度，采用非线性有限元方法求解所需的内力及位移(端部弯矩、吊杆体的挠度和测量截面的应变)，根据实测的内力及位移参数识别抗弯刚度。

(3) 弯矩的理论识别方法。根据实测的端部压力分布，考虑非线性效应，根据挠度和应变推求抗弯刚度。

2.2　试验结果

非线性静力求解法由于横向位移较小，横向力较小时受测试精度影响，分析结果很不理想，但在最后两级试验荷载时，将实测数据利用有限元进行试算模拟，相关参数可保持一致，识别的抗弯刚度与频率法测试识别的也基本一致，起到了验证效果，频率法试验结果见表1，利用下式计算出吊索刚度。

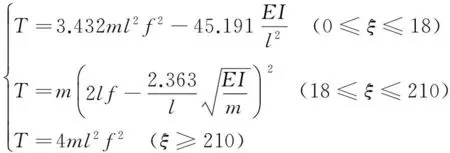
表1　短吊索试验结果　Hz

通过对比分析，确定出吊索在其使用荷载下的抗弯刚度EI=1.24e9mm2, 是钢丝叠加抗弯刚度的2.84倍，但仅为换算整体截面抗弯刚度的3.9%。利用实测抗弯刚度对吊索横向受力进行计算分析，考虑刚度折减后短吊索受力可满足要求，可取消球形转动铰。

3结语

通过采用频率法和非线性静力求解法对吊索抗弯刚度的识别，按修正后的抗弯刚度对对吊索受力进行分析后取消了短吊索的球形转动装置，有利于日常养护，研究结论可供存在短吊索的工程参考。但必须认识到在不同荷载作用下，吊索抗弯刚度变化很大，其值与吊索内部结构形式、钢丝间粘结强度、结构试验状态等有关，是一个不易识别的参数，工程应用时应以实际测试为准。采用非线性静力求解法时，应事先对试验方案进行详细规划，避免因测试精度不足造成结果分析困难。

参考文献

[1]陈舒婷,吴惠君,范中林,等.考虑弯曲刚度及边界约束的短索内力识别[J].交通科技,2013(1):26-28.

[2]凌知民,沈红,沈炯伟.吊杆索力的计算方法与应用研究[J].石家庄铁道大学学报,2011(3):35-36.

Identification for Flexural Rigidity of Short Suspension Cable

Based on Frequency Method and Nonlinear Static Method

WangJinjun1,LiWanxia1,HeYouwei

(1.No.6 Eng. Co. Ltd. of CCCC Second Harbor Engineering Co., Ltd., Wuhan 430014, China;

2.Hubei Xingda Road & Bridge Co., Ltd., Xianning 437100, China)

Abstract：Suspension cable bending stiffness is related to a variety of factors. As an unknown parameter, the suspension cable bending stiffness is difficult to be identified accurately in actual engineering. In this paper a 3m long sling being made up of 5mm diameter high-strength galvanized steel wires is selected as the research subject. The frequency method and nonlinear static solution are used to estimate short sling bending stiffness. Amended bending stiffness is taken to stress analysis of the sling. The results show that the spherical rotation means of the short sling can be canceled, which will reduce the project cost, and is beneficial to routine maintenance.

Key words:frequency; nonlinear; short suspension cable; stiffness; specimen; sensor; measure point

收稿日期：2015-08-15

DOI 10.3963/j.issn.1671-7570.2015.06.003