非线性H∞控制的SOS设计

何朕，王广雄，孟范伟

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨 150001 2.东北大学秦皇岛分校控制工程学院，河北秦皇岛 066004）

非线性H∞控制的SOS设计

何朕1，王广雄1，孟范伟2

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨 150001 2.东北大学秦皇岛分校控制工程学院，河北秦皇岛 066004）

提出了一种新的非线性H∞控制的设计方法。虽然平方和（简称SOS）方法可用来求解不易用解析法求解的非线性问题，但还是不能直接来求解HJI不等式或非线性的有界实不等式。详细分析了SOS法在求解中的这些局限性。给出了求解非线性H∞控制的一种迭代设计的方法。每一次迭代分为两步。第一步是先用SOS法设计系统的非线性状态反馈，其增益阵是可调整的。第二步是求系统L2增益，用图解解析法求解计算中的优化问题。还给出了一个卫星大姿态机动的非线性H∞控制设计作为应用本方法的实例。

非线性H∞控制;平方和;HJI不等式;有界实引理;姿态控制

0 引言

L2增益的控制问题，习惯上也称为非线性H∞控制［1－2］。这是因为H∞范数虽是在线性系统的传递函数上定义的，不过如果转换到时域上来考虑，这H∞范数就是L2诱导范数，而在非线性系统中则称之为L2增益。L2增益的控制是指以L2增益作为系统设计时的性能指标，使之尽可能小。本文研究的是以L2增益为性能指标的非线性状态反馈律的设计。非线性H∞控制虽然在理论上可以用Hamilton-Jacobi-Issacs（HJI）不等式来求解［1－2］，但HJI不等式目前还没有一个有效的解析求解的方法。近年来出现的SOS方法［3－5］，为求解非线性H∞控制问题提供了一个新的可能途径。SOS是平方和（sum of squares）的缩写。SOS法是指采用SOS多项式来研究非线性系统。除了对象本身的非线性特性，如果想采用高于二次型的Lyapunov函数，或者想设计高阶次的非线性控制律，就得研究一般形式的多项式。如果相应的系统的多项式可整理成SOS形式，那就一定是非负的。这个方法虽然才问世不久，但已经在一些重要的应用领域显现出了其优越性，例如非线性系统吸引域的估计［6－7］，大机动下的卫星姿态控制［8－9］，飞机的姿态控制［10］，非线性模型预测控制［11］，时滞系统的稳定性分析［12－13］，等等。在非线性H∞控制方面也提出了一些采用SOS的设计方法［14－16］。但这些方法在应用中都存在一些问题。关于现有这些SOS法在求解中的问题，由于要用到一些公式，所以在第3节再对这些现有方法来进行评述，并进而提出一种新的求解非线性H∞控制的方法。

1 系统方程式和基本公式

设非线性系统可整理成如下的状态依赖的类线性（linear-like）微分方程式［14］

式中x为状态变量，w为外输入，z为性能输出。并设A（x），B1（x）和C1（x）为x的多项式矩阵。此类系统也可称为多项式非线性系统。

对于给定的标量γ＞0，如果对于任意的T＞0，且x（0）=0时有

非线性系统（1）、（2）的稳定性和L2增益可以用下列的Hamilton-Jacobi不等式来确定［1－2］

式中V（x）为存储函数，V（x）≥0，V（x0）=0。如果系统是零状态可观测的［1－2］，则V（x）就是Lyapunov函数。

根据式（4），利用Schur补引理，很容易得出与线性系统中平行的下列的多项式非线性系统的有界实引理。

引理1［15］如果存在一个正定的Lyapunov函数V（x）能满足下列条件，则式（1）、（2）的系统稳定，且其L2增益小于等于γ。

式（4）是对应于一般系统（1）、（2）的一个最基本的不等式。当考虑控制问题时，系统方程式（1）中要另加有控制输入u。而对于H∞的设计问题来说，性能输出z中还需要有对控制输入u的加权，以便在设计中对x和u之间，即在误差大小和控制量大小之间进行适当的折衷。故非线性H∞控制问题中的系统方程式为

式中B2（x）和D12（x）也为多项式矩阵。

当考虑到式（7）时，Hamilton-Jacobi不等式（4）的第三项为

设u为状态反馈，根据式（6）、（7）和（3）可推导出求解此状态反馈的HJI不等式［1－2，17］

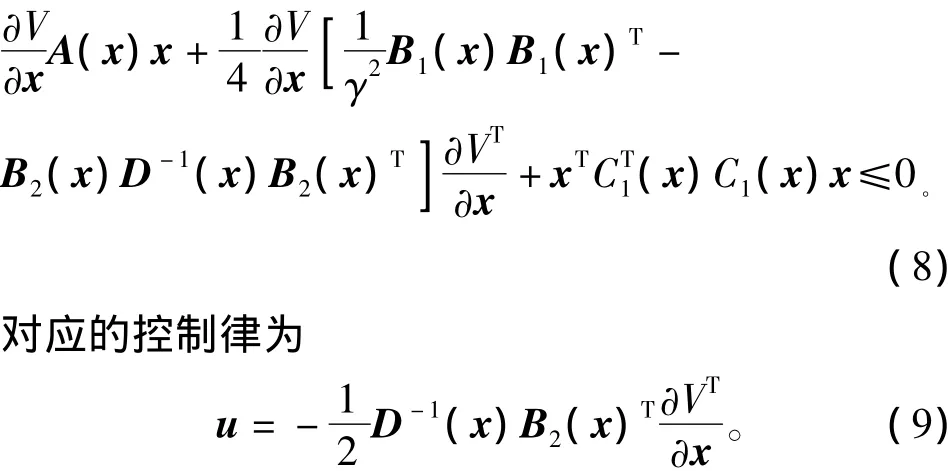
式（8）中B2D－1BT2项是将式（9）代入uTDu后得到的。式（8）就是求解非线性H∞控制的HJI不等式，求得存储函数V（x）后代入式（9）就可求得状态反馈律u。但这个HJI不等式却不容易求解。自从提出了SOS法，就会想到是否能用SOS来求解这个HJI不等式。

2 SOS方法

SOS是指平方和多项式。多项式是由有限个单项式的线性组合所构成，例如多项式

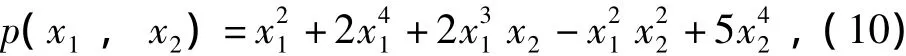
是由具有两个变量的5个单项式组成的。对一个多项式p（x1，…，xn）≜p（x）来说，如果存在多项式f1（x），…，fm（x）可以使p（x）写成平方和的形式，即

那么这样的多项式就称为SOS多项式，有时就简称为SOS。显然，每一个SOS多项式都是非负的，或表示成p（x）≥0。SOS多项式的集合用∑［x］来表示，如果一个多项式是SOS的，就写成

SOS多项式也可表示成下列的一种特殊的二次型形式

式中Q是半正定的对称阵，Z（x）是由阶次小于等于d的各单项式构成的列向量，而多项式p（x）的阶次则是小于等于2d。例如对于式（10）的多项式来说，

式（13）表明，SOS的求解可归结为线性矩阵不等式（LMI）问题。现在都有现成的软件可供使用，软件的名称是SOSTOOLS，可从网上下载［3］。

3 非线性H∞控制

SOS方法是用数值求解法来求解不容易解析求解的非线性问题，所以一经提出就有人试图用SOS法来求解非线性H∞控制中的HJI不等式［14］。但是事情进展得并不顺利。对于SOS法在HJI求解中所遇到的难题，下面先来分析状态反馈问题的求解。而且这状态反馈也将是本文方法的一个组成部分。

对于状态反馈问题，设系统的方程式为

式中A（x）和B（x）是x的多项式矩阵，x∈Rn，u∈Rm。

取系统的Lyapunov函数为

式中P阵是一常数阵。

对于式（15）的系统，如果采用如下的状态反馈律

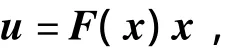
那么在dV/dt的求解中

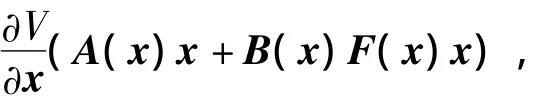
会出现P和F的相乘项而不能构成凸问题。这里可以采用LMI法中常用的做法，在求解中取P阵的逆阵［18］。具体做法是先取非线性的状态反馈律为

取Q=P－1，并注意到式（16）的P是正定的，故Q也是正定的。对式（18）中各项均左乘和右乘一个Q阵，得

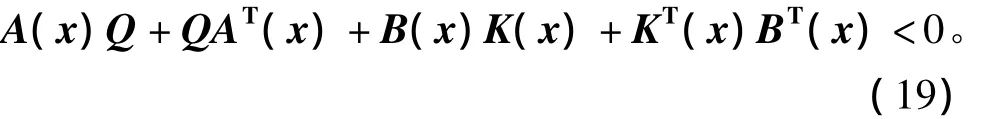
P阵取逆以后，式（19）的不等式中，待求的Q阵和K阵都呈仿射关系，这就可以用SOS法来求解了。

现在来分析HJI不等式（8）的求解问题。对于式（6）的类线性系统，系统的Lyapunov函数一般取为［14］

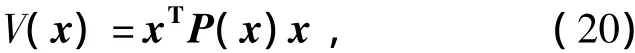
式中P（x）为一多项式矩阵。为了说明计算中的问题，这里暂设这个P阵为常数阵，这时

将式（21）代入式（8），可以看到这HJI不等式是一种Riccati型的不等式，不是仿射型的。在LMI法中，对于Riccati型不等式一般也是将其解求逆来得出一个线性不等式［17］。文献［14］在求解HJI不等式时也采取这种做法，提出用Q=P－1使式（8）形成一种仿射关系。这样就可以用SOS来求解了。但是作为非线性H∞控制来说，求得HJI的解后还得从式（9）求控制律u，而从式（9）和（21）可以看到，这要求将这个逆P－1正过来。这样问题就来了，因为一个多项式矩阵的逆不可能仍旧是一个多项式矩阵。也就是说，文献［14］的这个方法在SOSTOOLS软件上是无法求解的。事实上，文献［14］以及随后的一些文献的举例［16］中都只举P阵是常数阵的例子。但如果P是常数阵，并设系统的输入阵B2也是常数阵，那么从式（9）（21）可以看到，所得的控制律u便是一个线性控制律。这就又回到了非线性H∞控制的早期的工作［2］。

文献［15］提出了另一种用SOS来迭代求解非线性H∞控制的方法。这个求解法用的是有界实引理中的不等式（5）。将式（6）整理成

将式（22），式（7）与式（1）、（2）相对应，代入式（5），整理后可得状态反馈下的有界实不等式为

对每个固定的状态反馈律ui－1（x），不等式（24）是一个凸问题，可用SOS方法来求解，得Vi（x）和γi。这里第一个（初始的）Lyapunov函数取为V0（x）=，并借用式（9）来求得第一个u0。其后各步的Lyapunov函数取为

式中M（x）为设定阶次的单项式的列向量。此M（x）是在用SOS法求解不等式（24）时来求取的。求得Vi（x）后再借用式（9）计算ui。每次迭代计算后观察所得的γi，如果γi是在减少，可继续迭代。否则，则停止。

这个方法的主要问题是在第一步，要求V0=下有解。注意到P0是常数阵，如果要V0下有解，就意味着首先存在一个线性的状态反馈解，而且是全局稳定的。这就对所研究的非线性系统加上了限制，否则要对所用的SOS算法加上其他约束条件。这个方法的第二个问题是，用式（9）来计算每一步的ui并没有严格的理论依据，只是从HJI不等式的一种“借用”。由此可见，这第二种利用SOS来求解非线性H∞控制的方法，也不是完美的，也是有限制的。但至少它可以通过式（25）的高阶次Lyapunov函数获得非线性的控制律，较上面的正面求解HJI不等式的第一种方法是前进了一步。

非线性H∞控制虽然可以通过HJI不等式（8）或非线性有界实不等式（23）来求解。但是如上所述，用SOS法来正面求解这两个不等式都存在着相应的困难。与之对比的是，同样是通过P阵的求逆来获得仿射型的不等式，但状态反馈问题中的解［式（17）］与HJI的解［式（9）］是不一样的。式（17）中当P为常数阵时还可以通过求解K（x）来获得非线性控制律，而在HJI问题中SOS法则受制约于多项式矩阵的求逆，可见状态反馈问题是既简单又可充分发挥SOS方法的特点。基于这个认识，本文提出一个新的求解非线性H∞控制的迭代方法，每一次迭代中分两步来进行计算。第一步是先求解状态反馈问题，得非线性控制律ui（x），第二步是用图解解析法求解Hamilton-Jacobi不等式（4），得系统的L2增益γi（见下面算例中的具体说明）。如果这个γi值不满足要求，则修改状态反馈设计，再重复上述的计算。这里说的修改状态反馈设计是指修改式（17）中的反馈增益K（x）。一般来说，L2值偏大往往是因为反馈增益不够大，就应使增益取较大的值。有时也可能是因为反馈增益过大，系统容易起振而使L2值偏大，则就要限制系统的反馈增益。是增加或是减小，可视响应曲线（例如图3）而定。注意到这个K（x）是多项式矩阵，K（x）中的各元就是SOS设计中的（多项式）决策变量，只要限定K （x）中各元的取值范围，就可以改动整个状态反馈的设计。而限定决策变量的取值范围，只是要在算法中增加一个不等式约束［3］，这在SOS法中仅仅是一种举手之劳。例如要求K（x）中某一个系数的范围为K6＜－2，即－2－K6＞0。将－2－K6写入（加入到）SOS的程序prog中的语句就是

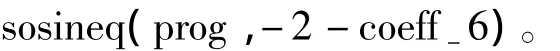
SOS问题的求解本来就是求解一组多项式不等式，在这一组不等式中增加一些对某个系数的不等式约束，对于用SOSTOOLS来求解根本不存在的问题。这个加上增益约束的状态反馈解是第一步，下面的图解法求解L2增益是第二步。第一个回合如果要求增加（或减少）反馈增益，可以回过来修改第一步中的约束范围，进行第二个回合，使之逐步达到最优的性能值γ。这个新的求解方法既充分发挥了SOS法的特点，又简单易行。

4 非线性H∞控制算例

现在以一卫星姿态机动控制为例，来说明本文提出的分两步来进行迭代的方法。这是一个具有6个状态变量的非线性系统，目前尚无其他有效方法可以来求解此类高维系统的非线性H∞控制问题。这里的第一步是先用状态反馈法来求控制律u。卫星的运动方程式包括动力学方程和运动学的微分方程。设卫星为刚体，其动力学方程为

式中:Ix，Iy，Iz为相应轴的转动惯量，ωx，ωy，ωz为绕相应轴的角速度分量，Tx，Ty，Tz为相应轴的控制力矩。

根据欧拉定理，刚体绕固定点的任一位移可绕通过此点的某一轴转动一个角度而得到。这个轴称瞬时转轴，在姿态控制中也称特征轴（eigenaxis），用k表示，k=［n1，n2，n3］T，并用φ表示转动的角度。本文采用修正的Rodriguez参数（Modified Rodriguez Parameters，MRPs）来表示卫星的姿态［19］，MRP可适用于（特征轴）转动到360°。MRP参数（向量）与（k，φ）的关系为

采用MRP时卫星的运动学微分方程式为［19］

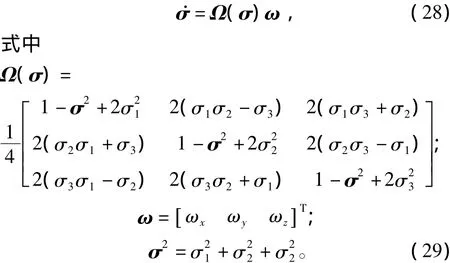
式（26）和式（28）构成了卫星姿态运动的非线性微分方程。设状态向量则可将式（26）和式（28）整理成状态依赖的类线性方程式

其中aij为式（26）、式（28）中各对应项的系数。

设刚体卫星的惯性阵I=diag（15，16，12.5） （kg·m2），将I代入式（30）就可按式（19）的思路用SOS法来进行状态反馈设计。这里取文献［20］所得的状态反馈律作为这第一步的解，为

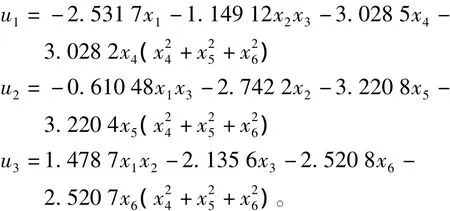
这里要说明的是，本例的状态反馈问题的不等式（19）是一个6×6的多项式矩阵。所谓多项式矩阵，是指矩阵中的每一元都是多项式，都是一些具有6个变量的高阶多项式。因此待求的各个系数，即求解中的决策变量数的计算量非常大，这种不等式约束的求解只能靠SOS法。图1就是在此控制律作用下的姿态（σ）和角速度（ω）的响应曲线。初始角速度为零，初始时刻的姿态对应于绕特征轴k转动一个角度φ=200°，k=［0.5028，－0.669 3，0.546 9］T。对应的姿态参数MRP为σ（0）=［0.5992，－0.7976，0.6517］T。

文献［20］主要研究SOS设计中的数值误差问题和姿态大机动控制下的饱和控制问题，这里则是在求得此控制律后进一步来求解系统的L2增益。这就是第二步，求解γ看是否满足性能要求。求L2增益就是要解有界实引理［式（23）］，上面已经分析了正面求解有界实引理中的问题。所以这里提出一种直接求解Hamilton-Jacobi不等式（4）的方法。定义不等式（4）的左侧部分为Hamilton函数H［21－22］，即

图1 姿态控制系统的响应曲线Fig.1Topology of fire alarm controller

这个Hamilton函数是与有界实引理1相对应的。当加上反馈形成闭环系统时［见式（22）］，这个Hamilton函数就成为

这里在计算L2增益时只对系统的输出变量加权而不对控制量u加权，即取式（7）中的D12=0。在本例的姿态控制中，性能输出就是姿态变量σ=［σ1，σ2，σ3］T的加权［参见式（27）］，故取

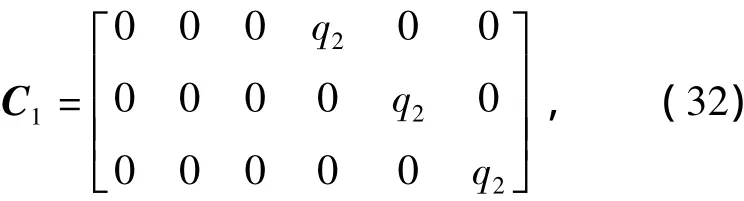
式中q2是对各姿态变量的加权系数，是这里的寻优问题中的一个决策变量。

本文的思路是在状态反馈设计后再来求解系统的L2增益。因此这一步中已经有了一个正定的Lypunov函数。文献［20］中的V（x）=xTPx，而求解所得是其逆阵Q=P－1，即由于正定阵乘以正数仍是正定的，所以这里是以已经求得的这个Lyapunov函数V（x）作为基本函数再乘以一个系数KV形成式（31）中的一个新的正定函数，这个KV是寻优过程中的另一个决策变量。

现在Hamilton函数式（31）中的变量是x，γ，q2和KV，可写成H［x，γ，q2，KV］。这样，L2增益的求解就转化成如下的一个优化问题了。

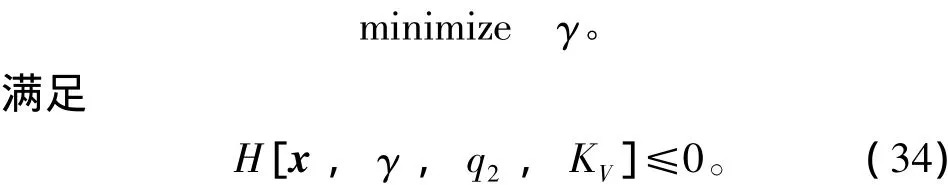
注意到式中的q2是对输出的加权，如果q2=1，那么L2增益的意义就更为清晰，所以可以先取q2= 1来开始寻优。这样，现在的决策变量就只有γ和KV了。要求解这个优化问题，就是要看式（34）这个H是否小于等于零。如果这是一个二阶系统，则只要将状态变量x1和x2划分为网格，各个网格点上的H值形成一个曲面，如果曲面的最高点≤0，即为最优解。可是本例中的状态变量是6维的，数值寻优中数据量是很大的，而且也不易用图解来表示。注意到结合具体的Hamilton函数来说，式（34）的超平面应该是连续的，不存在突变点。所以可以取一条斜穿整个状态空间的特定的轨迹线来进行寻优。具体来说，在式（34）中使每一个计算点的状态变量都为同一个值，即x1=x2=…=x6=c，使c从－10到+10共取2×104点进行寻优。当KV=104时得γmin=0.42。图2所示就是对应于这个γmin的Hamilton函数（实线）。作为验算，若γ=0.41时这Hamilton函数就开始上翘，即H≥0。图2的图形表明，对这类寻优问题来说，因为Hamilton函数的超平面是连续的，一条斜贯穿的轨线就足以反映出H是否总是小于零。取这样的特定轨迹线来寻优，既方便又实用。

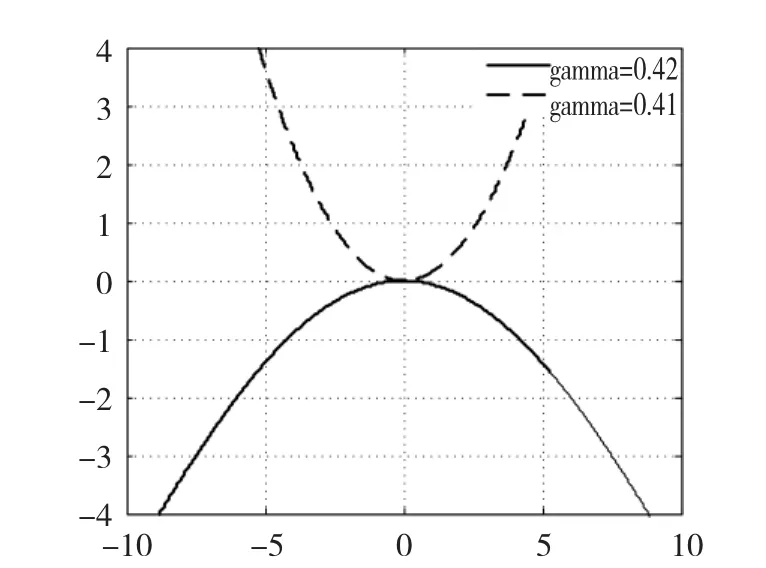
图2 Hamilton函数图Fig.2Hamiltonian function

现在来考察所设计系统的L2增益。设在卫星的x、y、z轴上分别加上分段的常值扰动ωx、ωy和ωz:

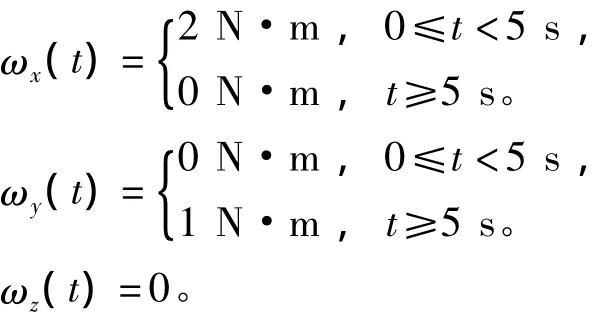
图3所示就是在这些扰动力矩作用下，姿态输出（σ）的响应曲线。

根据w（t）和输出的响应曲线σ（t）可以计算有限区段［0，T］内输入到输出的截断2－范数‖z‖2，T/‖w‖2，T如图4所示。式中

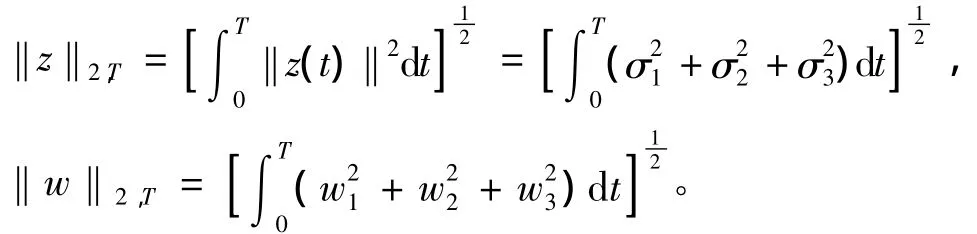
图3 扰动作用下的输出响应Fig.3Output responses under disturbance

图4中还用虚线标出了上面设计所求得的γ值0.42。根据图4和式（3）可知，所设计系统的L2增益小于等于γ=0.42。当然这里只是一个特定的扰动信号下的例子，对于任何的截断L2函数，其增益都是小于等于0.42的。这个L2增益在本例中就是系统的扰动抑制（disturbance attenuation）特性。如果这个扰动抑制特性不满足设计要求，就要修改状态反馈设计，即修改式（17）中的反馈增益K（x），再重新计算L2增益γi+1

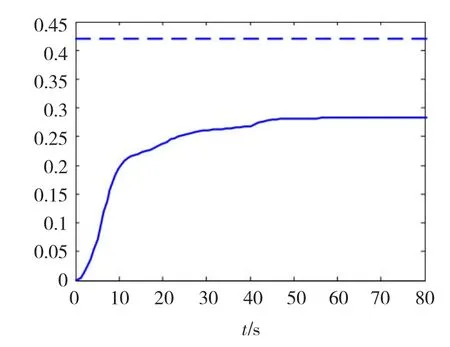
图4 截断2－范数Fig.4Topology of fire alarm controller

5 结论

SOS方法是一种数值求解方法，可以求解不易解析求解的非线性问题。但SOS在使用时仍有本身的一些限制条件，实际上还不能正面的、一次性的来求解HJI不等式或有界实不等式。本文提出分成两步来求解非线性H∞控制问题，在解状态反馈解和修改状态反馈解时能充分发挥SOS法的优点，而在求解L2增益时则采用图解解析法来寻优，为非线性H∞控制问题提供了一个简便实用的求解方法。

［1］VAN DER SCHAFT A J.L2－gain analysis of nonlinear systems and nonlinear state feedback H∞control［J］.IEEE Trans Automatic Control，1992，37（6）:770－784.

［2］申铁龙.H∞控制理论及应用［M］.北京:清华大学出版社，1996:223－234.

［3］PRAJNA S，PAPACHRISTODOULOU A，PARRILO P.Introducing SOSTOOLS:A general purpose sum of squares programming solver［C］//Proceedings of the IEEE CDC，Las Vegas，USA.2002:741－746.

［4］JARVIS-WLOSZEK Z，FEELEY R，TAN W，et al.Some controls applications of sum of squares programming［C］//Proceedings of the IEEE CDC，Maui，USA.2003:4676－4681.

［5］ZHAO D，WANG J L.Robust static output feedback design for polynomial nonlinear systems［J］.Int J Robust and Nonlinear control，2010，20（14）:1637－1654.

［6］TAN W，PACKARD A.Stability region analysis using polynomial and composite polynomial Lyapunov functions and sum-of-squares programming［J］.IEEE Trans Automatic Control，2008，53（2）: 565－571.

［7］TOPCU U，PACKARD A，SEILER P.Local stability analysis using simulations and sum－of－squares programming［J］.Automatica，2008，44（10）:2669－2675.

［8］GOLLU N，RODRIGUES L.Control of large angle attitude maneuvers for rigid bodies using sum of squares［C］//Proceeding of the 2007 American Control Conference，July 11－13，2007，New York City，USA.2007:3156－3161.

［9］PRAJNA S，PARRILO P A，RANTZER A.Nonlinear control synthesis by convex optimization［J］.IEEE Trans Automatic Control，2004，49（2）:310－314.

［10］KRISHNASWAMY K，PAPAGEORGIOU G，GLAVASKI S，et al.Analysis of aircraft pitch axis stability augmentation system using sum of squares optimization［C］//Proceedings of the 2005 A-merican Control Conference，July 8－10，2005，Portland，USA.2005:1497－1502.

［11］FRANZEÉ G.A nonlinear sum－of－squares model predictive control approach［J］.IEEE Trans Automatic Control，2010，55 （6）:1466－1471.L［12］PAPACHRISTODOULOU A，PEET M M，LALL S.Analysis of polynomial systems with time delays via the sum of squares docomposition［J］.IEEE Trans Automatic Control，2009，54（5）:1058－1064.

［13］ZHANG Y，PEET M，GU K.Reducing the complexity of the sum-of-squares test for stability of delayed linear systems［J］.IEEE Trans Automatic Control，2011，56（1）:229－234.L

［14］PRAJNA S，PAPACHRISTODOULOU A，WU F.Nonlinear control synthesis by sum of squares optimization:a Lyapunovbased approach［C］//Proceedings of the ASCC，2004:157－165.

［15］ZHENG Q，WU F.Nonlinear output feedback H∞control for polynomial nonlinear systems［C］//2008 American Control Conference，June 11－13，2008，Seattle，USA.2008:1196－1201.

［16］黄文超，孙洪飞，曾建平.一类多项式非线性系统鲁棒H∞控制［J］.控制理论与应用，2012，29（12）:1587－1593.

HUANG Wenchao，SUN Hongfei，ZENG Jianping.Robust H-infinity control for a class of polynomial nonlinear systems［J］.Control Theory and Applications，2012，29（12）:1587－1593.

［17］王广雄，何朕.应用H∞控制［M］.哈尔滨:哈尔滨工业大学出版社，2010:93－94，172－174.

［18］CHILALI M，GAHINET P.H∞design with pole placement constraint:an LMI approach［J］.IEEE Trans Automatic Control，1996，41（3）:358－367.

［19］TSIOTRAS P.Further passivity results for the attitude control problem［J］.IEEE Trans Automatic Control，1998，43（11）: 1597－1600.

［20］何朕，孟范伟，王广雄，等.卫星大角度姿态机动控制的SOS设计［J］.中国空间科学技术，2013，33（5）:69－75.

HE Zhen，MENG Fanwei，WANG Guangxiong，et al.SOS design for control of large attitude maneuvers of satellites［J］.Chinese Space Science and Technology，2013，33（5）:69－75.

［21］SINHA P K，PECHEV A N.Nonlinear H∞controllers for electromagnetic suspension systems［J］.IEEE Trans Automatic Control，49（4），2004:563－568.

［22］AHMED M S.Neural controllers for nonlinear state feedback L2-gain control［J］.IEE Proc Control Theory Appl，2000，147（3）: 239－246.

（编辑:张诗阁）

SOS design for nonlinear H∞control

HE Zhen1，WANG Guang-xiong1，MENG Fan-wei2
（1.School of Astronautics，Harbin Institute of Technology，Harbin 150001，China 2.School of Control Engineering，Northeast University at Qinhuangdao，Qinhuangdao 066004，China）

A new design method for nonlinear H∞control was proposed.Though sum of squares（SOS） method can be used to solve analytically unsolvable nonlinear problems，but it still cannot be used directly to solve the Hamilton-Jacobi-Issacs（HJI）inequality or the nonlinear bounded-real inequality.The restrictions of the SOS method were discussed in detail.An iterative design procedure for nonlinear H∞control problems was presented.There are two steps in each round of iteration.The first step is to design the nonlinear state feedback with adjustable gain matrix by using the SOS method.The second step is to solve an optimal problem in computation of the L2-gain by using a graphical－analytical method.A nonlinear H∞control design for large attitude maneuvers of statellites was presented as an application example of the proposed method.

nonlinear H∞control;sum of squares（SOS）;Hamilton-Jacobi-Issacs inequality;bounded real lemma;attitude control

10.15938/j.emc.2015.01.012

TP 273

A

1007－449X（2015）01－0082－08

2014－03－18

国家自然科学基金重点资助项目（61034001）;国家自然科学基金资助项目（61174203，60374027）

何朕（1972—），女，博士，教授，研究方向为控制系统设计、鲁棒控制及H∞控制等;

王广雄（1933—），男，教授，研究方向为控制系统设计、鲁棒控制及H∞控制等;

孟范伟（1981—），男，博士，讲师，研究方向为鲁棒控制。

何朕