矩形压电陶瓷振子的耦合振动

徐　洁,　田　华，　林书玉

(陕西师范大学　物理学与信息技术学院，　陕西　西安　710119)



矩形压电陶瓷振子的耦合振动

徐洁,田华*，林书玉

(陕西师范大学物理学与信息技术学院，陕西西安710119)

摘要：利用等效弹性法分析了矩形压电陶瓷振子的二维耦合振动，通过引入等效弹性常数和二维耦合系数得出矩形压电陶瓷振子的共振频率方程和耦合系数方程，探讨了耦合系数、共振频率与压电振子宽长比的依赖关系。利用数值法对压电振子的振动特性进行了模拟及仿真，并与解析结果进行了比较，二者吻合较好。最后用实验进行验证，实验结果与仿真结果有很好的一致性。

关键词:等效弹性法；耦合振动；耦合系数；共振频率

压电体的耦合振动在理论上和工程上都十分重要[1],多年来一直是人们感兴趣的课题。压电材料也因具有使机械能和电能相互转换的功能，被广泛用于设计具有特殊性能的声学器件，如压电频率器件[2]、压电超声换能器、陶瓷滤波器[3]以及陶瓷共振器[4]等。20世纪70年代，有限元法被用于分析压电结构，其主要用于分析自适应板的静态、模态、谐振、瞬态的线性行为[5-11]。

在实际应用中，压电陶瓷振子的几何尺寸是有限的，不能简单地认为振子都工作于单一的振动模式。事实上压电振子的振动模式是不同方向振动模式之间的相互作用[12]，其各个方向振动模式之间总是存在不同程度的耦合。本文运用等效弹性法，分析矩形压电陶瓷振子的二维耦合振动，探讨矩形压电振子的共振频率与尺寸的关系，利用ANSYS软件模拟不同尺寸下矩形振子的共振频率，并将数值结果与解析结果进行对比，最后用实验进行验证。

1矩形压电振子的二维耦合振动理论

1.1　耦合振动的分析

图1为矩形压电陶瓷振子的示意图，极化方向为z轴方向，电极面垂直于z轴，长度、宽度和厚度分别用a、b、t表示，并设a≫t，b≫t，又由压电振子的振动为二维振动，所以z方向的应力Tz=0。

图1　矩形压电振子Fig.1　Rectangular　piezoelectric　vibrator

若忽略压电振子的压电效应，在垂直于z轴的平面内振子被看成各向同性，即有

(1)

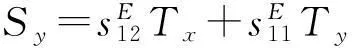
(2)

其中Sx、Sy表示x、y方向的应变，Tx、Ty表示x、y方向的应力，sE表示电场强度为零时的弹性柔顺常数。

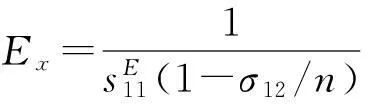
kxa=(2i-1)π，i=1,2,3,

(3)

kyb=(2j-1)π,j=1,2,3。

(4)

利用方程(3)、(4)可以得到

(5)

(6)

σ12(2i-1)2b2n2-[(2j-1)2a2-(2i-1)2b2]n-

σ12(2j-1)2a2=0，

(7)

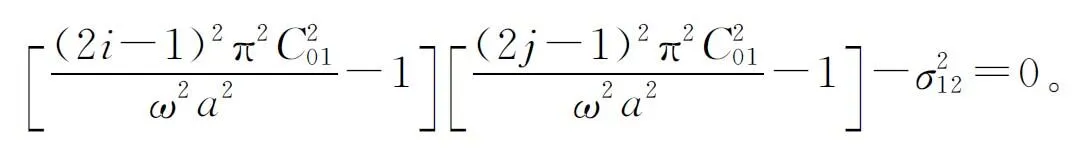
(8)

根据方程(7)、(8)可以解得两个共振角频率和两个耦合系数，分别为x方向和y方向的共振角频率和耦合系数，即矩形压电陶瓷振子的振动是x方向和y方向伸缩振动的耦合。

1.2　耦合系数与宽长比的关系

由方程(7)得到耦合系数n与宽长比k的曲线，如图2所示。

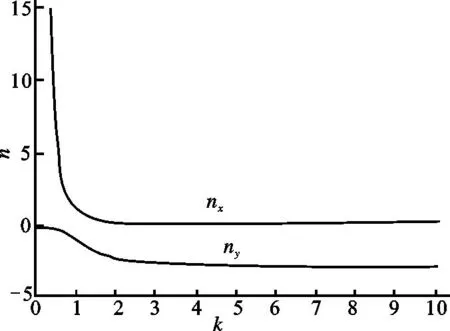
图2　耦合系数n与宽长比k之间的关系Fig.2　The　theoretical　relationship　between　couplingcoefficient　and　the　ratio　of　width　to　length

由图2可以发现：1.矩形振子二维耦合振动有两个耦合系数，一个为正数，一个为负数。耦合系数n为负数表示当矩形振子的长度在伸长时，宽度在缩短；耦合系数n为正数表示当矩形的长度在伸长时，宽度同时在伸长;2.方程(7)解得的两个耦合系数与方程(8)解得的两个共振频率具有对应关系。由方程(5)或(6)可以得到其对应关系：耦合系数n为正数对应沿长度x方向的共振频率fx，记为耦合系数nx；耦合系数n为负数对应沿宽度y方向的共振频率fy，记为耦合系数ny;3.当k的值为1，即矩形振子的长和宽相等时，耦合系数nx=1，ny=-1。此外，当矩形的长度与宽度尺寸相差很大时，耦合系数在一定范围内趋于稳定。

2矩形压电陶瓷振子的共振频率与

尺寸的关系

由方程(8)可得到矩形压电振子的共振频率与宽长比的关系，用ANSYS软件模拟材料为PZT-4，长度a=25mm，厚度t=1mm，k=b/a，激励电压为1V，k取不同值时的共振频率，并将解析解与数值解进行比较，比较结果如图3所示。本文中的归一化频率均为计算频率与其最大频率的比值。

图3表示矩形振子的长度大于宽度时，归一化共振频率fx′、fy′与宽长比k的关系。由图3可以发现，当长度一定，x方向的长度大于y方向的宽度时，fx′和fy′的数值解与解析解误差均较小；当长度一定，宽度逐渐增大时，归一化共振频率fx′、fy′均逐渐减小。

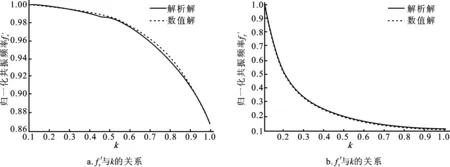
图3　k<1时归一化共振频率与宽长比k的关系Fig.3　The　relationship　between　the　resonance　frequency　and　the　ratio　of　width　to　length　with　k<1

图4表示矩形振子的宽度大于长度时，归一化共振频率fx′、fy′与宽长比k的关系。由图4可得，当长度一定，矩形振子的宽度大于长度时fx′的数值解与解析解误差非常小。当振子的宽度大于长度两倍时，fy′的解析解与数值解相差较大，其原因是在利用等效弹性法推导方程时进行了近似计算。此外，当长度一定，宽度逐渐增大时，归一化共振频率fx′、fy′均逐渐减小。

图4　k>1时归归一化共振频率与宽长比k的关系Fig.4　The　relationship　between　the　resonance　frequency　and　the　ratio　of　width　to　length　with　k>1

3实验验证

表1　矩形压电振子在x方向共振频率的解析结果、数值结果和测量结果Tab.1　　The　resonance　frequency　of　the　analytical　solution,　numerical　solution　and　the　measurement　results　in　the　x　direction

表2　矩形压电振子在y方向共振频率的解析结果、数值结果和测量结果Tab.2　The　resonance　frequency　of　the　analytical　solution,　numerical　solution　and　the　measurement　results　in　the　y　direction

由上表可以发现，等效弹性法得出的共振频率、ANSYS软件模拟得出的共振频率，均与实验得出的共振频率接近。

4结论

本文运用等效弹性法分析了矩形压电陶瓷振子的二维耦合振动，得出耦合系数方程共振频率方程，分别探讨了耦合系数、共振频率与矩形振子宽长比的关系，用有限元模拟得出了数值结果。结果发现，数值结果与解析结果相吻合，并且二者均与实验值相接近。

参考文献：

[1]周利生.矩形压电振子的多维耦合换能器理论[J].声学与电子工程,1993,29(1):16-21.

[2]陈伟,王海华,陈水琴.新型结构的片式压电陶瓷频率器件研制[J].电子元件与材料，2013,32(9):65-67.

[3]陈倩,阙良全,刘光聪.低频宽带陶瓷滤波器[J].压电与声光，2012,34(2):236-239.

[4]李环亭,孙晓红,陈志伟.压电陶瓷材料的研究进展与发展趋势[J].现代技术陶瓷，2009,30(2):32-36.

[5]王占军,周建方.压电结构有限元分析的动向[J].河海大学常州分校学报,2002,16(4):17-22.

[6]刘炜,吴运新.超声换能器ANSYS建模及谐响应分析[J].科学技术与工程，2009,9(10):2728-2731.

[7]AlanRB,SaravananMP,RaoVD,etal.Finiteelementapproachtomodelandanalyzepiezoelectricactuators[J].TheJapanSocietyofMechanicalEngineersInternationalJournalSeriesC,2001,44(2):476-485.

[8]莫喜平.ANSYS软件在模拟分析声学换能器中的应用[J].声学技术,2007,26(6):1279-1290.

[9]高琴.压电陶瓷材料参数对有限元结果的影响研究[J].黄山学院学报,2013,15(5):9-12.

[10]范兴明,马世伟,张鑫,等.基于ANSYS的压电陶瓷晶片PZT仿真分析[J].压电与声光,2014,36(3):416-420.

[11]吕航,范明庆,孙超.基于ANSYS的矩形压电振子瞬态特性分析[J].微特电机,2012,40(3):34-37.

[12]皇磊落,朱秀丽，牛勇，等.二维振动方向变换器的耦合振动[J].压电与声光,2008,30(4):425-427.

[13]林书玉.超声换能器的原理及设计[M].北京：科学出版社,2004:26.

[14]徐洁,林书玉.矩形压电振子的二维振动分析[J].声学技术,2014,33(4):72-74.

〔责任编辑李博〕

第一作者：刘小荣，男，硕士研究生，研究方向为超声检测。E-mail:lxrzxr@163.com

Thecoupledvibrationofrectangularpiezoelectricceramicvibrator

XUJie,TIANHua*,LINShuyu

(SchoolofPhysicsandInformationTechnology,ShaanxiNormalUniversity,

Xi′an710119,Shaanxi,China)

Abstract:Usingtheequivalentelasticmethod,two-dimensionalcoupledvibrationofrectangularpiezoelectricceramicvibratorisanalyzed.Resonancefrequencyequationandcouplingcoefficientequationoftherectangularpiezoelectricceramicvibratorareobtainedbyintroducingequivalentelasticconstantsandtwo-dimensionalcouplingcoefficients.Theaspectratiodependenceoftheresonancefrequencyandcouplingcoefficientisinvestigated.Numericalmethodisusedtosimulatethevibrationofrectangularpiezoelectricceramicvibrator,andthesolutionsofthesimulatedresultsarecomparedwiththosefromtheanalyticalmethod.Finallytheexperimenthasbeenpreformedtoverifythenumericalresults.Itcanbefoundthatexperimentalresultsareingoodagreementwiththeanalyticalandthesimulatedresults.

Keywords:equivalentelasticmethod;coupledvibration;couplingcoefficient;resonancefrequency

通信作者：*贺西平，男，教授，博士生导师。E-mail:Hexiping@snnu.edu.cn

基金项目：国家自然科学基金资助项目(11374201)

收稿日期：2014-07-18

doi:10.15983/j.cnki.jsnu.2015.02.224

文章编号：1672-4291(2015)02-0038-04

中图分类号:O426.1

文献标志码:A