采用遗传-谐振算法求解网格依赖任务安全调度问题
2015-02-22王洪峰
王洪峰, 朱 海
(1 华中科技大学 计算机科学与技术学院, 湖北 武汉 430079;
2 周口师范学院 计算机科学与技术学院, 河南 周口 466001)
采用遗传-谐振算法求解网格依赖任务安全调度问题
王洪峰1,2,朱海2
(1华中科技大学计算机科学与技术学院,湖北武汉430079;
2周口师范学院计算机科学与技术学院,河南周口466001)
摘要:针对异构网格环境下任务调度面临的安全性问题,考虑网格节点的系统安全控制策略与历史行为表现,构建了网格节点安全评估模型,并在此基础上提出了一种安全可信的网格依赖任务调度优化模型。为求解该模型,结合遗传算法全局寻优能力较强的特性,同时克服其局部寻优不足的缺点,引入谐振算法,从而设计了一种新的遗传-谐振算法(GASHO)。首先,针对DAG任务图基于启发式思想设计遗传进化算子和量子谐振算子等操作以产生任务调度优先队列,解决离散解非法的问题;然后,采用安全约束下的最早完成时间算子操作实现任务集到网格节点的映射,提高算法收敛效率;最后,对算法的时间复杂度和收敛性进行分析证明。仿真实验结果表明,在同等条件下与同类算法相比,GASHO算法在收敛性、调度长度、安全效益值等方面具有明显的优势。 同理,网格资源节点可依据其采用的提取(Hash函数)和身份认证机制(如数字签名技术)的类型,得到节点完整性和真实性水平值分别为和。
关键词:网格计算;依赖任务;安全调度;遗传-谐振算法
MRsubjectclassification:68M20
网格以统一框架将互联网中闲置的计算资源、存储资源、网络资源等组成一个超级计算系统[1],为超大型复杂应用任务提供计算服务。如何将计算任务调度配置到各类资源,使网格应用系统获得高性能成为研究的关键问题之一。相对传统任务调度,网格系统对任务调度策略提出了更高的要求[2-3]。近年来,该问题吸引了不少学者的关注,如文献[4]将安全因素融入同构网格即时任务调度场景,但其尚未关注真实网格场景所体现的异构与动态等特征。文献[5]在充分考虑网格节点动态性的基础上,借鉴社交网络模型,融合历史信誉度和自我评价信誉度两个方面,建立节点信誉度评价机制,但没有考虑网格资源节点本身的安全性。文献[6]对网格资源信任机制和任务调度机制相互分离的不足提出了建设性意见,但没有量化网格资源安全信任值,要在网格具体应用环境中实施,还需进一步研究。另外,网格调度研究主要针对元任务的简化应用场景[7-11],限制了网格应用场景。本文针对网格环境静态依赖任务调度问题,结合网格节点历史行为信誉度(动态信誉度)和自我认知信誉度(静态信誉度)两个方面,建立网格用户任务模型和资源节点拓扑模型,并基于此提出网格可信调度优化模型。该模型将网格系统任务调度长度性能、安全性能等需求结合起来,使网格任务调度在满足任务依赖关系的前提下,任务调度长度和安全效益值达到最优。
网格具有很多区别于其他分布式并行计算系统的特征,其任务调度模型相对比较复杂[12-16]。例如张伟哲等人建立了多目标约束的网格任务调度模型,基于多目标最优化理论及现代智能算法,设计并提出了一种多Qos约束[17]的网格任务调度算法[16],从时间、可靠性和安全性三个维度仿真网格计算环境及任务调度,并取得预期效果,但该算法中并未明确给出安全性、可靠性等量化定义。Xu等人针对异构计算系统中依赖任务调度问题,基于启发式遗传算法生成任务调度优先次序,同时采用EFT算法实现任务到网格的节点映射,对实时网格依赖任务调度具有较好的调度效果[18],但文章仅考虑了调度长度要素,未考虑安全等因素。Yalda等人针对异构分布式计算系统中的动态依赖任务调度问题,设计并提出了HSGA算法[19],该算法通过任务优先评价函数确定任务优先队列,同时考虑调度长度、调度失败率和负载均衡等性能指标,建立调度方案评估函数,融合启发式和遗传算法完成任务调度,仿真结果证明该算法在系统综合性能指标方面具有优势,但也未融入安全性因素。本文针对具有依赖关系的网格任务调度问题,提出了一种新的遗传-谐振算法。该算法在实数编码的基础上,基于启发式遗传算法思想重新设计改进了遗传算子,同时将遗传算法的结果作为谐振算法初始参数进行局部寻优,提高搜索精度,最后对算法进行了仿真实验,其结果表明该算法具有较好的综合性能。
1网格节点安全模型
网格节点安全性主要包括身份安全与行为安全两个方面。身份安全主要衡量网格节点的安全性,即对信息保密性、完整性、真实性等属性的支持度[20],行为安全则主要衡量网格用户对节点的评价。
定义1节点保密水平度量。假定网格系统限定采用加密算法类型N,则可通过理论分析与仿真实验得出每种加密算法的执行性能Pi,加密算法的最差性能为Pb,则可定义节点保密水平值为

(1)
定义2节点的安全效益。若仅考虑网格保密性、真实性、完整性等性能,则网格节点ru的安全值RS(ru)可通过如下公式计算:

(2)
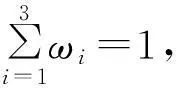
(2)式中ω1、ω2、ω3代表不同安全性能的权重。
网格节点在调度系统中的可信度直接影响网格调度系统的效率。本文借鉴社交网络安全信任机制,依据网格节点的历史服务行为表现优劣来确定其安全可信度。
定义3节点可信度度量。用来定义网格节点的可信赖程度,该度量标准主要由网格资源提供者节点静态评估PS(ru)和历史行为评估PD(ru),网格节点的可信度PC(ru)可由公式定义:
PC(ru)=PS(ru)+PD(ru)。
(3)
静态评估值PS(ru)主要受网格节点的安全水平RS(ru)、计算性能RP(ru)、可持续服务能力RC(ru)等因素影响,可由如下公式来定义:
PS(ru)=α·RS(ru)+β·RP(ru)+γ·e-RC(ru)。
(4)
公式中,α、β、γ表示权重系数,计算性能RP(ru)是依据实验测试网格节点执行不同类型任务的综合能力评价值,可持续服务能力RC(ru)是网格节点平均执行时长。
动态评估值PD(ru)主要受网格任务调度成功率AW(ru)、累计使用率AU(ru)、综合信任评价值AC(ru)等影响,可由如下公式定义:
PD(ru)=δ·AW(ru)+φ·AU(ru)+
θ·AC(ru)。
(5)
其中δ、φ、θ表示权重系数,AW(ru)代表网格节点i得到调度后,累计执行成功次数占总调度次数的比率,反映了网格节点的稳定性;AU(ru)代表网格节点成功执行任务总时长/网格待机服务总时长,反映了网格节点的可用性;AC(ru)代表网格节点ru累计执行任务获得的信任评价,包含平均执行长度、安全匹配情况和信誉度等因素,具体计算可参照文献[21]。
定义4节点安全模型。节点安全模型由节点安全效益和节点可信度组合而成,代表了该节点安全的综合效益值,若将任务ti分配到网格节点ru,则该任务执行时获取的安全总效益值可由下列公式计算:
Q(ti,ru)=μ1·RS(ti,ru)+μ2·PC(ti,ru),
(6)
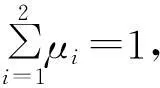
式中μ1、μ2分别代表属性安全和行为安全的权重,而RS(ti,ru)和PC(ti,ru)可在任务ti固定的情况下分别由公式(2)和(3)计算获得。
2网格依赖任务调度模型
2.1 网格资源与任务表示模型
具体来说,网格计算就是将一个大任务依据某种标准划分为N个子任务,然后将子任务按照某种策略调度到网格节点执行,最后汇总各节点执行结果形成最终结果。网格依赖任务模型[9]一般采用有向无环图(DAG)来表示,它是根据划分后的具有数据约束关系的网格任务业务处理流程建立的任务模型。DAG图中节点表示网格任务划分后的子任务,有向边表示任务之间的数据依赖关系。顶点的权值表示网格应用子任务的属性,如计算量和安全需求,而边的权值包括节点间的依赖关系,如通信数据传输量、数据在网格环境传输时的安全需求等。具体的网格任务图表示模型如图1所示。

图1 一个网格依赖任务图模型Fig.1 An example of dependent tasks graph model in grid
在DAG图中,没有父节点的任务节点称为根节点,没有孩子的任务节点称为终端节点。若图中存在多个根节点,则可通过虚拟节点和无依赖关系的边将其转换为单入口图。同理,也可将多终端节点的图转换为单出口图。任意任务节点的执行,必须在其所有父节点结果信息到达之后才能开始。
定义5依赖任务需求表示模型。依赖任务模型可表示为三维向量TD=(V,E,W),V是顶点集合,ti表示第i个子任务,|V|表示子任务的个数;E为边的集合且满足条件E={eti,j|ti∈V,tj∈V,i≠j},描述子任务之间的数据依赖关系集合;W为顶点权值集合,由Wti=(ati,sti)表示,ati和sti分别代表网格子任务ti的计算量和安全需求。
定义6网格资源表示模型。本文所研究的异构网格模型可由集合R={ru|u∈[0,m)}表示,对任一网格节点为一个三元组ru=(δu,ρu,τu),其中δu代表节点的计算能力,ρu表示节点的安全服务向量,τu代表网格节点的可持续服务能力。
2.2 可信依赖任务调度优化模型
基于网格资源与任务的建模表示,网格任务调度策略可体现为任务-资源映射图[2](如图2所示)。
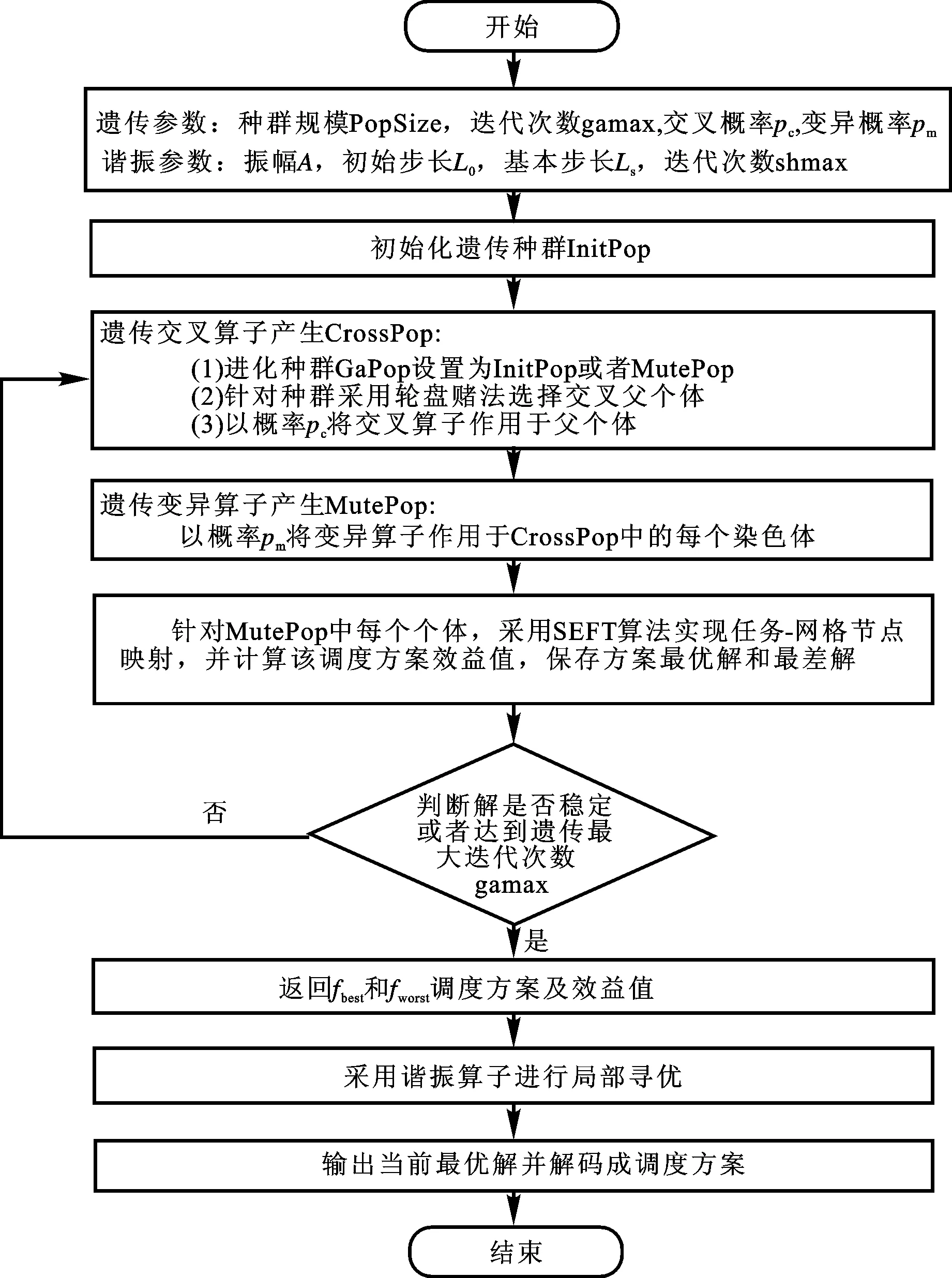
定义7网格任务-资源映射方案。网格任务资源分配映射图可以用一个向量TRG={l0,l1,…,l|V|}表示,其中lx={(ti,ru)|0≤i<|V|,0≤u 图2 网格任务-资源分配图模型Fig.2 Scheduling graph model for mapping tasks to grid nodes 定义8任务调度安全评估函数。该函数用来评价网格用户应用任务执行安全满意度,可由下式获得: (7) 很明显,S(Gk)∈(0,1),另Q(ti,ru)可由(6)式计算获取,Xiu是任务到资源的映射矩阵,为决策变量,即当任务ti分配到资源ru上执行则Xiu为1,否则为0。 定义9任务调度长度评价标准。任务调度长度TL(Gk)是指从网格任务开始执行时刻到最后一个子任务在网格系统中执行完成时刻之间的时间间隔,主要由任务的等待时间twti,ru、执行时间teti,ru和获取安全效益所花费时间tsti,ru组成(暂不考虑网格节点其他时间代价,如通信时间代价等),可由下式描述: TL(Gk)=twti,ru+teti,ru+tsti,ru。 (8) 显然,DAG图中出口任务节点一定是调度长度最长的,DAG图深度为m,则可通过每一层最长调度的递归求和获得出口节点的等待时间twti,ru,而teti,ru和tsti,ru可通过公式(9)和(10)计算获得。 tei,u=ati/δru, (9) (10) 其中,(10)式计算方法可查阅文献[22]。 定义10网格可信调度优化模型。本文网格可信调度优化目标是寻找依赖任务描述模型到网格节点模型之间的映射,使得网格系统执行任务时调度长度最短的同时,用户获得尽可能安全的网格执行环境。其数学模型表示如下: min(Z)=w1·TL(Gk)+w2(1-S(Gk)), (11) f(tj,rv)-f(ti,ru)≥a(tj)/δ(rv)+ts(tj,rv)。 在(11)式中,Z={z1,z2,…,zk},zk为第k个分配调度方案,即任务到资源的映射方案;TL(Gk)和S(Gk)为网格任务的调度长度和安全总效益值,可分别由(8)式和(7)式获得;w1、w2为调度长度与安全效益值的重要性权重,根据任务特性,适当调整权重wk(k=1,2),对任意目标进行重新优化以满足不同网格用户的倾向性需求。 3遗传-谐振算法设计 遗传算法和模拟谐振算法[23]都是指数级信息处理而提出的智能算法。遗传算法以全局并行搜索能力较强而著称,但却存在局部搜索能力较差等问题,容易陷入局部最优解。1994年,Rudolph详细分析了该现象的原因:遗传算法主要体现的是进化过程中父代和子代之间的继承和延续关系,可能存在不理想的组合,导致最终无法产生理想解。谐振操作具有较强的局部搜索能力,且收敛速度极快,但是却很难准确确定谐振系统的运行参数(一般是随机或者经验确定),从而影响解的质量。从算法运行机理上来看,两种算法互补性高。 因此,针对网格依赖任务调度NP难问题,本文充分利用遗传算法的宏观并行全局寻优能力,提高收敛速度;同时引入谐振操作增加种群个体的多样性以及提高局部寻优能力,以获得尽可能接近问题最优解的Pareto最优解,提高收敛质量。 评价函数主要用来评估新解优劣以决定取舍。针对本文异构网格依赖任务可信调度问题,采用可信调度优化模型中的适应度评估函数,基于高效低能时间复杂度EFT(EarliestFinishTime)算法,实现任务到网格节点的映射(由于本文引入安全要素,因此将基于EFT的算法称为安全约束下的EFT算法,简称SEFT)。网格系统依据历史行为等信息实时维护网格节点安全综合效益值,并按照降序排列得到网格节点序列RQ。具体任务节点映射到网格节点的算法如下: 算法1.任务-网格节点映射及效益评估算法SEFT 输入:任务调度优先队列 输出:最优和最差的任务调度方案及其效益值 Step1while调度队列SQ=∅,do Step2取队首任务t(i),并从SQ中移除t(i); Step3针对RQ队列的每一网格节点r(u),依次计算t(i)分配r(u)上的可信调度优化的综合效益值,获取Min(Z)与Max(Z); Step4基于Min(Z)与Max(Z)值,分别将任务t(i)分配到网格节点rmin(u)rmax(u),并记录到映射方案GoodMap、BadMap; Step5endwhile Step6返回GoodMap、BadMap、Min(Z)、Max(Z)。 依据算法步骤概述,初始种群主要任务是产生符合任务依赖关系的任务调度序列。为便于解码,染色体编码采用任务序号定长组合编码。为生成符合条件的初始解群体,首先将应用网格任务图(DAG)中的所有子任务节点按深度值划分成h层,第i层中的子任务构成集合DAG(i),0≤i 算法2.初始化种群InitPopulation 输入:依赖任务关系约束图DAG 输出:生成初始种群Pop[PopSize] Step1依据任务关系约束图按照深度值生成DAG(i)任务集合; Step2PopNo=1 Step3whilePopNo Step4fori=0;i Step5针对DAG[i]中的所有任务,随机生成一个序列进行编码,并将编码值追加到Pop[PopNo]编码后边; Step6i++; Step7endfor Step8PopNo=PopNo+1; Step9endwhile Step10return初始化种群Pop[Popsize]。 3.3.1遗传交叉算子设计遗传算法的优越性能主要取决于交叉算子设计。本文借鉴文献[24-25]采用启发式单点交叉原则实现交叉操作,既保证了任务依赖关系,也保证了交叉操作的正确性。启发式交叉的正确性原则:针对已有的任务调度序列,任意删除部分任务节点不影响原调度队列中任务节点间的依赖关系。具体交叉操作实现算法如下: 算法3.交叉操作 输入:双亲个体编码Fa、Ma 输出:交叉后的两个子个体编码C1、C2 Step1随机产生双亲交叉位p∈(1,|V|); Step2以交叉位p为断点,将父个体Fa和Ma分别分割为前后段,具体表示为Fa_L、Fa_R、Ma_L、Ma_R; Step3针对子个体C1:从Ma的任务基因组合中删除Fa_L包含的任务基因生成Ma′;将Fa_L和Ma′合并构成C1基因; Step4针对子个体C2:从Fa的任务基因组合中删除Ma_L包含的任务基因生成Fa′;将Ma_L和Fa′合并构成C2基因; Step5returnC1,C2。 3.3.2遗传变异算子设计通过突变因子,遗传算法一方面可使种群结构多样,另一方面可跳出局部最优解,并加速向全局最优解收敛。本文为保证变异操作产生解的合法性,只需要DAG任务图中任意子任务进行变异操作后满足条件:某子任务节点在新解中的相对位置不能置于其所有前驱节点之前,也不能置于其所有后继节点之后。在该条件下,变化任意两个子节点的位置都是合法的调度。因此本文采用启发式变异算子实现变异操作,即针对染色体中的任意变异点q,向前搜索第一个前驱节点pri(q),其位置为pq;向后搜索第一个后继节点suc(q),其位置为sq;则在(pq,sq)之间任意选择一个位置都可与q进行交换实现个体变异操作,且不会因为变异操作改变任务依赖关系。具体变异操作实现算法如算法4所示: 算法4.变异操作 输入:父个体Fa 输出:子个体Child Step1随机选择1个任务基因位pos; Step2从pos+1开始直到|V|,查找t(pos)的第一个后继节点位置late_pos;若没有,则late_pos=pos; Step3从pos-1开始逐步递减至1,查找t(pos)的第一个前驱节点位置pror_pos;若没有找到,则pror_pos=pos; Step4在[pror_pos+1,late_pos-1]之间产生随机整数rand_pos≠pos; Step5交换pos和rand_pos位置的任务基因信息,产生新个体Child; Step6returnChild。 3.3.3谐振算子设计 (1)模拟谐振算法的基本流程 模拟谐振算法(SHO)即仿生物理学中简谐振动原理搜索问题最优解的现代智能启发式算法。若将谐振系统运动点的位置坐标映射问题的解,振幅映射为解空间,采用系统的弹性势能作为适应度评价函数F,谐振基态(势能为0)映射为问题的最优解。模拟谐振算法具体流程请参阅文献[26]。 (2)谐振算子设计 谐振算法具有较强的搜索能力,但由于无法准确确定平衡点和端点等参数,从而影响解的质量与收敛速度。因此,首先将遗传算法获取的最优解和最差解作为谐振算法的平衡点和端点,消除初始解的随意性或人为因素,然后基于谐振算法进行解寻优,具体算法流程如下: 算法5.谐振操作算子 输入:GA的最优解、最差解的调度方案及其效益值 输出:最优调度方案及其效益值 Step1系统运行基本参数的初始化:将遗传算法运行获得的最优解和最劣解及其作为谐振系统的平衡点f(Init)和端点f(End);将计算资源的数目乘以任务的数量作为谐振系统的振幅A和初始步长L0(系统的能级)、基态步长Ls取值为2; Step2f(s)=f(Init); Step3首先采用2-opt产生新解s′,步长L∈[Ls,L0],计算适应度函数增量Δf=f(s′)-f(s);若Δf≤0,则接受新解s′为当前解,并记忆最小解;若Δf>0,且(Ls/L0)2-Δf/(f(End)-f(s))≥0,则接受新解s′为当前解,否则抛弃此新解[27];变化当前步长L,循环执行本步骤直到完成指定的计算步骤; Step4量子谐振操作阶段:步长范围为L∈[1,Ls],采用随机插入法(步长为1)产生新解;接受准则为:若Δf≥0,则接受新解s′为当前解,否则不接受;直至满足局部搜索终止策略; Step5打印当前最优解并退出算法。 本文的遗传谐振算法(GASHO)总框架如下:(1)依据DAG任务图中的数据依赖关系,基于启发式思想设计遗传进化算子和谐振算子等操作,产生不同的任务调度队列,提高搜索能力和搜索精度;(2)基于HEFT算法思想[27],采用安全约束下的最早完成时间算子操作,实现任务集到网格节点的映射,提高算法收敛速度和调度性能。GASHO算法流程如图3所示。 图3 GASHO算法流程图Fig.3 Algorithm flow chart of GASHO 定理1(全局收敛性)算法以概率1收敛到问题的全局最优解。 证明(1)在算法中,对于任意两个个体p和q,q可由p通过进化生成。 假设个体w=(w1,w2,…,wn)是由p=(p1,p2,…,pn)通过进化作用产生的任一后代,由进化过程可知,从pi产生wi的概率为1/(n-1),由此可得 P{E(p)=w}=(n-1)-1(n-1)-1… (n-1)-1=(n-1)-n>0。 由于个体参与进化的概率,则个体通过基因更新产生个体的概率为 P{E(p)=q}≥P(E(p)=w)·P(E(w)=q)= pg·(n-1)-n>0。 即对于可行解空间Q中任意两个个体p和q,q可由p进化所得。 (2)由GASHO算法的解个体更新过程可知,X(0),X(1),…,X(k)是单调的,即满足∀t,有 min{f(x)|x∈X(t+1)}≤ min{f(x)|x∈X(t)}。 因此,由证明(1)和(2)可知,GASHO算法以概率1收敛到依赖任务可信调度问题的最优解。 设m为网格节点数目,n为DAG图中任务总数,遗传算法种群个数为p,迭代次数为q,谐振过程的迭代次数为r。本算法的时间复杂度计算主要包括遗传过程和谐振过程两个部分。GA种群初始化的时间复杂度为o(np);遗传交叉和变异算子都是针对种群中的个体进行基因的遍历操作,因此时间复杂度为o(np);评价函数基于EFT算法,其时间复杂度为o(mn);故遗传过程的总时间复杂度为o(npq+mn)。由于谐振算法主要是针对1个解不断进化,其算法时间复杂度主要和进化过程(主要是评价函数计算)和进化次数相关,其时间复杂度为o(rmn)。因此,本算法的总体时间复杂度为o(mnp+npq+rmn)。 4仿真实验与结果分析 为了验证本文提出的GASHO算法的效性,首先采用VMWarevSphere5.0将4台IBMSystemx3850X5(每台8颗CPU,每颗CPU8核心,内存256GB)、1台IBMDS5020光纤存储(8GB光纤数据带宽、20TB存储容量)、万兆内部光纤网络等资源组建成集群。其次基于Java语言设计开发了网格仿真实验平台,该平台由组件GridProc、TaskProc和GridManager组成。其中组件GridProc主要负责模拟生成网格环境,具体依据设定的网格性能集合、网格安全策略效益集合(仿真环境网格节点安全值分布于{0.2,0.4,0.5,0.6,0.8,1.0})等随机产生具有不同性能、不同安全策略的网格资源节点;组件TaskProc主要依据用户需求生成计算量不同、安全水平要求不同的具有依赖关系的任务集合;GridManager则负责网格任务调度管理工作。下面分别从算法的收敛性能、任务的调度长度、安全效益等指标进行仿真实验,并将结果与SEFT算法、GA算法进行对比分析。 为比较算法的收敛性,图4给出了算法在60个网格节点、500个任务在500代迭代过程中的调度长度变化曲线。由于SEFT算法是启发式算法,图中显示了GA算法和GASHO算法的收敛性。 图4 GASHO和GA算法收敛性比较Fig.4 Convergence comparison between GAalgorithm and GASHO algorithm 由于GA算法和GASHO算法初始种群都是采用由启发式算法产生的同一种群,因此图4中曲线起始点相同,算法初始运行阶段,两类算法性能表现不相上下,但随着进化代数的增加,GASHO算法优势充分体现出来,其收敛速度和调度长度都明显优于GA算法。 为了进一步验证GASHO算法针对随机DAG任务图的调度性能,从两个方面进行了仿真:(1)任务数量固定但网格节点规模可变;(2)任务数量可变但网格节点规模固定。 (1)任务数量固定但网格节点规模可变。 为了验证算法的有效性和任务的多样性,实验随机产生了规模为200的DAG图共20组,并通过GridProc随机产生了规模为20、40、60、80、100、120、140、160的网格环境,每组网格环境的计算性能和安全策略都有所不同。实验针对同一网格环境下20组DAG图的调度效果进行均值分析,具体实验效果如图5所示。 从图5(a)中可以看出,在任务规模一定的情况下,随着网格节点规模的增加,任务调度长度都呈递减趋势,尤其是当网格节点数量较多时,调度长度性能几乎不分上下,这主要是因为随着网格节点数量的增加,在满足安全策略要求的前提下,任务在调度时可选择性能更好的网格节点执行,降低了调度长度,且总体来说GASHO算法的调度长度性能最好,尤其是任务数量相对网格节点数量较多时。从图5(b)看出,随着网格节点的增加,安全效益值都有所增加,这主要是网格节点数相对任务的并行度达到一定的倍数时,任务对网格节点的竞争趋缓。但是,同等条件下GASHO算法的安全效益值相对较稳定,而SEFT算法的安全效益值提升幅度更明显。 (2)网格节点固定但任务数量可变。 实验随机产生了60个异构网格节点,并通过TaskProc随机产生了任务数量规模为50、100、150、200、250、300、350、400的DAG图各20组,每类DAG图的最大并行度、深度、安全需求等都不相同。分析实验结果时,将任务数量相同的20组仿真结果求均值作为衡量标准,具体仿真结果如图6所示。 图5任务数量固定、网格环境可变情形下性能比较 图6 网格环境固定,任务规模可变情形下性能比较Fig.6 Performance comparison in the condition that fixed grid environment and variable tasks number 从图6a可以看出,在网格环境一定的情况下,随着任务规模的增加,任务调度长度都有所增加。相对来说,GA算法相对于SEFT算法有约10%的性能提升,而GASHO算法相对于GA算法又提升约3%,算法性能提升较小主要是因为GA和GASHO算法均以启发式SEFT算法为基础,基础解都较优秀所致。另外,通过分析实验数据来看,随着任务规模的不断扩大,三种算法的折线图开口越来越大,相对优势也越来越明显,因此GASHO算法更适于应用大规模任务情况。从图6b看出,在不同任务规模的情况下,由于SEFT算法侧重于强调调度长度最优,导致安全效益值相对最差;GA算法安全效益值相对SEFT算法较优,但比GASHO算法差。这体现在两个方面:一是GASHO算法的安全效益值更优,二是GASHO算法的安全效益值相对更稳定,这主要是因为增加了谐振搜索算子后,能搜索到性价比更好的解。 通过仿真实验可以看出:SEFT算法依据任务到达次序找到每个任务的局部最优调度长度,但不一定是全局最优解;GA算法虽然针对问题最优解具有较强的全局搜索能力,但容易陷入局部最优解;谐振算法不仅具有很好的全局收敛性,而且局部搜索能力也较强,但是很难确定初始运行参数;GA算法与谐振算法相结合,优缺点互补性高,获得了更好的收敛速度和全局收敛性。 5结语 本文首先针对网格依赖任务调度问题,结合网格节点的安全策略控制与历史行为表现,建立了网格资源节点安全模型,并以此为基础构建了可信调度优化模型,某些方面补充了相关研究工作。其次,利用遗传算法与谐振算法解寻优过程中优势互补的特征,结合EFT算法快速映射任务到处理机的思想,提出了一种针对异构分布式计算系统中DAG任务调度的遗传谐振算法GASHO,并从收敛性和时间复杂度方面进行了证明或分析。GASHO算法采用启发式策略控制遗传算子和谐振算子操作,在任务依赖约束条件下,可以更快更好地产生新的任务调度队列,达到全局与局部寻优的目的。最后,通过对随机DAG任务图和真实应用DAG图等进行实验,验证了GASHO算法在收敛速度、调度质量(包括调度长度、安全效益值满意度等)等方面具有较好的综合性能。 未来,将进行两个方面的工作:一是将相关研究工作迁移到云计算环境中,以期在用户SLA需求与系统运营策略(尤其是成本控制)等方面寻求最佳平衡点;二是进一步探讨云环境下服务定价机制与底层资源映射相结合的资源调度优化问题。 参考文献: [1]Shin-YeuL,Shih-ChengH,Cheng-ZihL.Expandingservicecapacitiesandincreasingservicereliabilitiesforthegrid-basedutilitycomputing[J].IEEETransactionsonSystems,Man,andCybernetics-PartA:SystemsandHumans,2011,41(1):149-160. [2]朱海,王宇平.融合安全的网格依赖任务调度双目标优化模型及算法[J].软件学报,2011,22(11):2729-2748. [3]SarkarV,KhapardeSA.Improvingdemandresponseandbid-consistencyofpriceoutcomeinthesecurity-constraineddispatchscheduling[J].IEEETransactionsonPowerSystems,2013,28(8):2433-2445. [4]GongChen,WangXiaodong,XuWeiqiang,etal.Distributedreal-timeenergyschedulinginsmartgridstochasticmodelandfastoptimization[J].IEEETransactionsonSmartGrid,2013,4(9):1476-1489. [5]YuanLL,ZengGS,JiangLL,etal.Dynamiclevelschedulingbasedontrustmodelingridcomputing[J].ChineseJournalofComputers,2006,29(7):1217-1224. [6]ZhangWZ,LiuXR,HuMZ,etal.Trust-drivenjobschedulingheuristicsforcomputinggrid[J].JournalonCommunication,2006,27(2):73-79. [7]BraunTD,SlegelHJ,BecjN.Acomparisonofelevenstaticheuristicsformappingaclassofindependenttasksontoheterogeneousdistributedcomputingsystems[J].JournalofParallelandDistributedComputing,2001,61(6):810-837. [8]XiaoP,HuZG.Co-schedulingmodelforindependenttaskswithdeadlineconstraintincomputationalgrid[J].ActaElectronicSinica,2011,39(8):1852-1857. [9]马艳,龚斌,邹立达.网格环境下基于复制的能耗有效依赖任务调度研究[J].计算机研究与发展,2013,50(2):420-429. [10]阎朝坤,胡志刚,李玺,等.面向可靠性-费用优化的网格任务调度模型及算法研究[J].计算机科学,2013,40(5):136-141. [11]DuXL,JiangCJ,XuGR.AgridDAGschedulingalgorithmbasedonfuzzyclustering[J].JournalofSoftware,2006,17(11):2277-2288. [12]殷国富,罗阳,龙红能,等.并行设计子任务调度的遗传算法原理与实现方法[J].计算机辅助设计与图形学学报,2004,16(8):1122-1126. [13]HeXS,SunXH,vonLaszewskiG.QoSguidedmin-minheuristicforgridtaskscheduling[J].JournalofComputerScienceandTechnology,2003,18(4):442-451. [14]WengC,LuX.Heuristicschedulingforbag-of-tasksapplicationsincombinationwithQoSinthecomputationalgrid[J].FutureGenerationComputerSystems,2005,21(2):271-280. [15]ChenJ,KongL,PanX.ResearchongridresourceschedulingalgorithmintegratingforecastmechanismwithQoSconstraint[J].JournalofComputerResearchandDevelopment.2008,45:11-16. [16]张伟哲,胡铭曾,张宏莉,等.多QoS约束网格作业调度问题的多目标演化算法[J].计算机研究与发展,2006,43(11):1855-1862. [17]AbdelzaherTF,AtkinsEM,ShinKG.QoSnegotiationinreal-timesystemsanditsapplicationtoautomatedflightcontrol[J].IEEETransactionsonComputers,2000,49(6):1170-1183. [18]XuYuming,LiKenli,HuJingtong,etal.Ageneticalgorithmfortaskschedulingonheterogeneouscomputingsystemsusingmultiplepriorityqueues[J].InformationSciences,2014,270(2):255-287. [19]YaldaAryan.HSGA:Ahybridheuristicalgorithmforworkflowschedulingincloudsystems[J].ClusterComputing,2014,17(5):129-137. [20]袁文成,朱怡安,陆伟.面向虚拟资源的云计算资源管理机制[J].西北工业大学学报,2010,28(5):704-708. [21]ZhuH,WangYP.Security-driventaskschedulingbasedonevolutionaryalgorithm[C]//Proceedingsofthe2008ComputationalIntelligenceandSecurity,Washington:IEEEComputerSociety,2008:451-456. [22]ZhuH,WangYP.GriddependenttaskssecurityschedulingmodelandDPSOalgorithm[J].JournalofNetworks,2011,6(6):850-857. [23]陈发堂,张民仓.一类新的环状非有心谐振子势的精确解[J].陕西师范大学学报:自然科学版,2011,39(4):29-33. [24]徐雨明,朱宁波,欧阳艾嘉,等.异构系统中DAG任务调度的双螺旋结构遗传算法[J].计算机研究与发展,2014,51(6):1240-1252. [25]JinXu,AlbertYSLam,VictorOKLi,etal.Chemicalreactionoptimizationfortaskschedulingingridcomputing[J].IEEETransactionsonParallelandDistributedSystems,2011,22(10):1624-1631. [26]朱思峰,刘芳,柴争义,等.简谐振子免疫优化算法求解异构无线网络垂直切换判决问题[J].物理学报,2012,61(9):096401. [27]TopcuogluH,HaririS,WuMinyou.Performanceeffectiveandlow-complexitytaskschedulingforheterogeneouscomputing[J].IEEETransactionsonParallelandDistributedSystems,2002,13(3):260-274. 〔责任编辑宋轶文〕 第一作者:姚洪兴,男,教授,博士生导师,研究方向为经济系统复杂性建模与分析。E-mail:hxyao@ujs.edu.cn Usinggenetic-harmonicalgorithmtosolvesecurityschedulingproblem ofdependenttasksinheterogeneousgridsystem WANGHongfeng1,2,ZHUHai2 (1SchoolofComputerScienceandTechnology,HuazhongUniversityofScienceand Technology,Wuhan430079,Hubei,China; 2SchoolofComputerScienceandTechnology,ZhoukouNormalUniversity, Zhoukou466001,Henan,China) Abstract:Aimedatthesecurityproblemoftasksschedulinginheterogeneousgridsystem,asecurityevaluationmodelispresentedbasedonsecuritycontrolstrategyandhistorybehaviorofgridnodes,andonthisbasisakindofsafeandtrustedoptimizationmodelfordependenttasksschedulingisputforwardundergridenvironment.Tosolvethemodel,anewgenetic-harmonicalgorithmcalledGASHOisdesigned,whichtaksfulladvantageofthecharacteristicofglobaloptimizationofgeneticalgorithmandintroducestheharmonicoperatortoovercometheshortageoflocaloptimization.BasedonthedependenciesofaDAGtaskgraph,theheuristicmethodisemployedtodesigntheoperatorofgeneticandquantumharmonic,thustheGASHOproducesabettertaskschedulingqueuetoavoidtheoccurenceofillegalsolutionsindiscretespaces.Then,toimprovetheconvergenceefficiency,theearliestfinishtimeoperatorwhichisconstrainedtosecurityfactorsisusedtomapfromtasksettogridnodes.Atlast,theconvergencepropertyandtimecomplexityisanalyzed.Comparedwithothersimilaralgorithmunderthesamecondition,thesimulationresultsshowthattheproposedalgorithmhastheadvantagesontheconvergenceproperty,schedulinglengthandsecurityefficiency. Keywords:gridcomputing;dependenttask;securityscheduling;genetic-harmonicalgorithm 基金项目:国家自然科学基金资助项目(71271103,71371087,71271107) 收稿日期:2014-10-10 doi:10.15983/j.cnki.jsnu.2015.02.221 文章编号:1672-4291(2015)02-0024-04 中图分类号:TP393 文献标志码:A

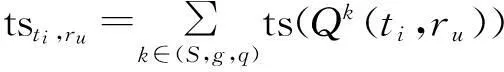


3.1 解质量评价函数
3.2 初始种群生成
3.3 算子设计
3.4 算法流程描述
3.5 算法收敛性分析
3.6 算法时间复杂度分析
4.1 算法的收敛性分析

4.2 随机产生任务DAG图

Fig.5Performancecomparisonintheconditionthatfixedtasksnumberandvariablegridenvironment
