变量对称性问题的计算分析
2015-02-22汲守峰
汲守峰,刘 卉
(唐山学院 基础教学部,河北 唐山 063000)
变量对称性问题的计算分析
汲守峰,刘 卉
(唐山学院 基础教学部,河北 唐山 063000)
高等数学中很多问题的求解涉及函数的多个自变量,如果某几个自变量具有奇偶性或定义域关于坐标原点、坐标轴、坐标面对称,就可以利用变量的对称性简化计算过程。
函数奇偶性;变量对称性;简化计算
0 引言
高等数学中的很多问题在计算时若考虑变量的对称性会大大简化计算过程。在多元函数微分学中,自变量之间若具有对称性,则函数对处于对称位置的自变量求偏导数时其结果类似[1]。多元函数积分学中,某个自变量在积分区间对称时,以定积分关于自变量的对称性或奇偶性为基础[2],也会减小计算的难度。在应用拉格朗日乘数法[3]计算有多个变量问题的条件极值时,对变量进行对称性分析可有效简化方程组[4],从而简化计算过程。本文通过以下几个实例,分析变量对称性问题的方便解法,并应用Matlab软件验证结论。
1 对称性问题的计算分析
1.1 利用对称性求解拉格朗日乘数法目标函数的极值
对目标函数的自变量加以限制的条件极值问题,通过引入拉格朗日函数的方法,为找到内部可能存在的最值点提供了可行的解决办法。但在对各个自变量求偏导得到的方程组求解时,可能会因变量个数过多导致求解困难,而多数条件极值问题其变量之间往往具有对称性,考虑对称性可充分简化方程组及减少变量个数,使计算变得简单。
例1 求函数f(x,y,z)=x4+y4+z4在满足条件xyz=8时的极值。
解 引入拉格朗日函数:f(x,y,z,k)=x4+y4+z4+k(xyz-8),
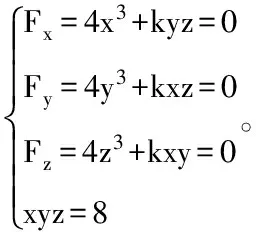
利用Matlab R2012a Command Window命令窗口获得该非线性方程组的解:
>>syms k x y z real
[k,x,y,z]=solve('4*x^3+k*y*z=0','4*y^3+k*x*z=0','4*z^3+k*x*y=0','x*y*z=8')
k=vpa(k,3),x=vpa(x,3),y=vpa(y,3),z=vpa(z,3)
运行结果:
k=
-8.0
-8.0
-8.0
-8.0
x=
2.0
-2.0
-2.0
2.0
y=
2.0
-2.0
2.0
-2.0
z=
2.0
2.0
-2.0
-2.0
得到4个驻点(x,y,z)为C1(2,2,2),C2(-2,-2,2),C3(2,-2,-2),C4(-2,2,-2),函数值均为48。根据对称性,只需对其中一个点进行说明,比如C1(2,2,2),f(C1)=48。
考虑第一卦限在曲面xyz=8上,
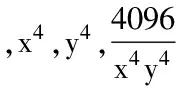
所以函数h(x,y)的最小值只能在闭区域D的内部取得,而其内部只有一个可能的极值点(2,2),故(2,2)是函数h(x,y)的极小值点,即P1(2,2,2)是f(x,y,z)的极小值点。
由变量的对称性可知C2(-2,-2,2),C3(2,-2,-2),C4(-2,2,-2)也是f(x,y,z)的极小值点,极小值为48。
1.2 利用变量对称性求超越方程根的个数

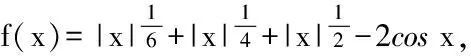
当x≥2时,易知f(x)≥0,那么只需讨论f(x)在[0,2]内零点的个数。
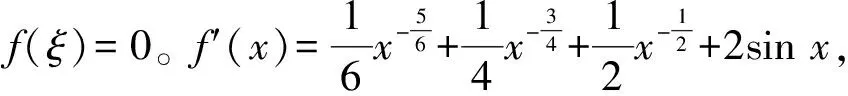
利用Matlab R2012a Command Window命令窗口获得该超越方程的正解。
设函数y=x^1/6+x^1/4+x^1/2-2*cos(x),求其正根
>>p=2;
y=inline('x^1/6+x^1/4+x^1/2-p*cos(x)','x','p');
[x,yx]=fzero(y,[0,5],[],p)
运行结果:
x=
1.0623
yx=
-1.1102e-16
再输入命令:
>>x=-2∶0.1∶2
y=abs(x)^1/6+abs(x)^1/4+abs(x)^1/2-p*cos(x)
plot(x,y,'-ro')
grid on
title('y的函数图像')
xlabel('x')
ylabel('y')
legend('y=abs(x)^1/6+abs(x)^1/4+abs(x)^1/2-2*cosx')
输出图1。

图1 函数y在区间[-2,2]上的图像
1.3 具有对称性的二重积分的计算
若D关于x(y)轴对称,D1是D位于x(y)轴上(右)方的部分,f(x,y)是D上连续函数,则
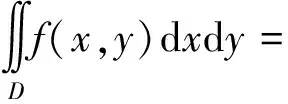
解 原积分区域D不具有对称性,添加辅助线y=-sinx,将D分成两部分D1,D2(见图2),对于D1:f(x,y)=f(x,-y),是关于y的偶函数;对于D2:f(x,y)=f(-x,y),是关于x的偶函数。
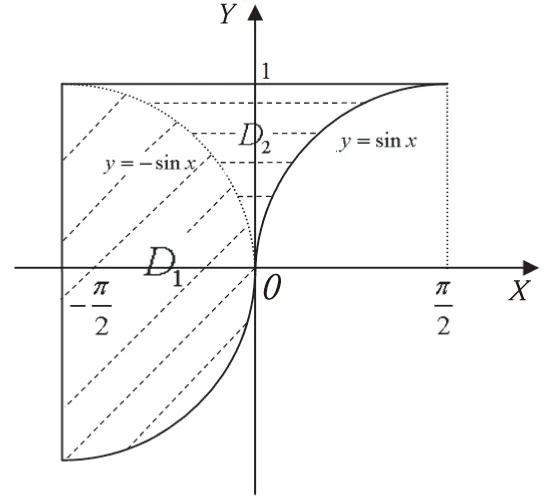
图2 积分区域D的图形
因为yxf(x2+y2)为y或x的奇函数,所以

通过添加辅助线使得积分区域变成关于坐标轴对称的区域,再根据被积函数的某一项或几项的奇偶性进行运算,明显简化了运算过程。
1.4 利用对称性计算曲面积分
若曲面∑关于xoy(或yoz或zox)坐标面对称,曲面∑1是曲面∑位于xoy上方(yoz前方或zox右方)的部分,f(x,y,z)在曲面∑上连续,则
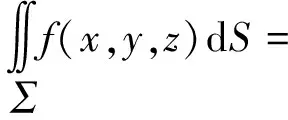
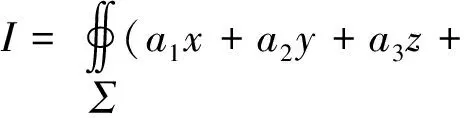


由x,y,z的对称性,有
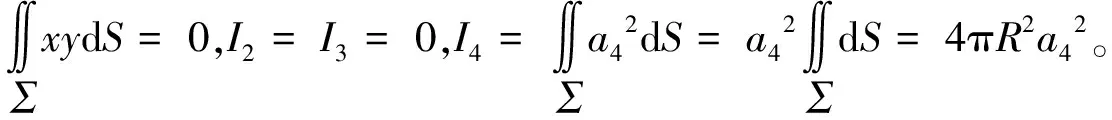
所以I=I1+I2+I3+I4=
2 结语
利用变量对称性对求解的问题进行简化计算,除上述讨论情形外,还可以应用于三重积分、对弧长的曲线积分、对坐标的曲线积分及计算偏导数等方面。若不考虑变量的对称性直接计算,则过程较为繁琐,同时也容易出错,而利用变量的对称性可使计算过程大幅简化,也便于检查。
[1] 廖为鲲.浅谈具有对称性的二重积分的解法[J].科教导刊,2013(4):172.
[2] 杨罗辉,张玲.一类二重积分的简便算法[J].高等函授学报:自然科学版,2005(19):27-30.
[3] 同济大学数学系.高等数学:下册[M].7版.北京:高等教育出版社,2007:116-121.
[4] 刘秀君.考研高等数学选讲[M].北京:清华大学出版社,2013:61-62.
(责任编校:夏玉玲)
An Analysis and Calculation of Variable Symmetry
JI Shou-feng, LIU Hui
(Department of Fundamental Science Teaching, Tangshan College, Tangshan 063000, China)
Many problems in higher mathematics are related to multiple variables of functions. If certain independent variables have parity or the definition domain on coordinate origin, the axes, and the coordinate plane are symmetrical, simplified calculation can be achieved through variable symmetry.
parity of function; variable symmetry; simplified calculation
O172.2
A
1672-349X(2015)05-0011-03
10.16160/j.cnki.tsxyxb.2015.06.005
