考虑空间拱效应的筒形墙体主动土压力

陈国舟，周国庆

(1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008;2.河南省城乡规划设计研究总院有限公司，河南郑州 450000)

筒形挡土墙由于其良好的受力和变形特性在矿井井筒、圆形基坑等地下工程中得到广泛应用.确定作用在筒形挡土墙上的土压力大小是筒形墙体设计的关键.目前对筒形挡土墙土压力的确定主要采用平面挡土墙理论或者经验公式.朗肯和库伦平面土压力理论由于简单易理解得到广泛应用，但这两种土理论适用于平面结构，且得到的土压力沿深度线性分布，而现有的室内试验及现场实测结果均表明作用于筒形墙体上的土压力沿深度呈非线性分布［1］.有学者提出了筒形墙体土压力理论.H.M.Westergaard根据滑动楔体的静力平衡条件得到了圆柱形孔周边应力分布.K.Terzaghi在H.M.Westergaard基础上，得到作用在竖井结构上的土压力，土压力沿深度非线性分布，计算公式如下:

式中:n1=R/r;r为井筒半径;a=tan2(45°+φ1/2);φ1=φ -5°.

V.G.Berezantzev［2］根据 Haar ＆ Von Karman 假定，在主动状态时，筒形墙体周边土体向圆心移动，形成滑动圆锥体，在水平方向存在圆环挤压效应，并假定环向应力等于第一主应力，得到作用在筒形挡土墙上主动土压力的简化解析解:

式中:Rb=r+ztan(45°-φ/2);r为井筒半径;γ为土体自重;φ 为内摩擦角;η =2tan φtan(45°+φ/2).

E.G.Prater［3］则采用库伦的滑裂面理论，引入切向力.假定切向应力与竖向应力的比值应介于K0和1之间，根据静力平衡条件得到主动土压力理论解.但其理论值在达到某一深度后将为0，其结果与实测值、试验值均不符，其土压力计算公式如下:

Cheng Y.M.等［4］、Liu F.Q. 等［5］在 V.G.Berezantzev滑移线场方法［2］求解筒形挡土墙土压力理论基础上，引入环向应力系数，得到考虑墙-土摩擦角、墙后填土倾斜、堆载等复杂情况下的土压力理论公式.但他们只考虑了主动状态时的环向挤压效应，而忽略了筒形墙体竖直向拱效应.K.Ueno等［6］由试验证明了竖向拱效应的存在对筒形墙体主动土压力分布及大小有重要影响.T.Fujii［7］也提出试验值与理论值的差异主要由竖向土拱效应引起.

K.Terzaghi由活动门试验证实存在土拱效应，并将土拱效应定义为由土体抗剪强度实现屈服区域土压力传递到未屈服区域的现象.随后大量实测及室内试验均证明土拱效应影响土压力大小及其分布.K.H.Paik等［8］通过理论值与试验值的比较，证实两者结果吻合较好.彭述权等［9］对理论值与试验值进行比较，认为考虑拱效应的土压力理论值较不考虑土拱效应的土压力解更能反应挡土结构的实际受力.可见，考虑竖向拱效应的土压力理论在平面挡土结构的土压力研究方面已取得不少成果，但筒形挡土墙由于其结构的特殊性，仅考虑竖向拱效应是不合适的.马英明［10］认为筒形挡土墙主动土压力受竖向拱和水平拱的共同作用，将筒形挡土墙土压力传递现象归结为“垂直成拱，水平呈环，拱环效应，地压减缓”.R.C.K.Wong等［11］则通过采用CCM方法，得到考虑水平拱、竖向土拱效应的土压力方法，与实测值比较认为考虑空间拱效应的土压力与实测值吻合较好.

现有对于筒形墙体主动土压力的研究均考虑其环向效应，而忽略竖向拱效应，笔者拟在 E.G.Prater［3］研究基础上，考虑环向拱和竖向拱效应，得到作用在筒形挡土墙上的主动土压力解析式，对土压力影响因素进行分析，并与现有理论解及离心试验结果进行比较.

1 分析模型

1.1 土体滑移面

合理选定土体滑移面形状是准确获得土压力的关键.对于平面挡土墙，库伦假定其滑移面为一平面，并在实际工程中得到广泛应用.对于筒形挡土墙，V.G.Berezantzev［2］假定滑移面为与水平面呈(45°+φ/2);K.Terzaghi则假定滑移面半径随深度增加而逐渐趋于定值;Y.W.Shin等［1］针对筒形挡土墙研究发现，在其后土体达到主动极限状态时，其滑移面与水平面的夹角大于(45°+φ/2).本研究为简化模型，对于筒形挡土墙后的土体滑移面，采用库伦方法，假定筒形挡土墙后土体滑移面为一平面.由库伦理论可知:当挡土墙竖直、光滑时，滑楔体与水平面的夹角为(45°+φ/2);当挡土墙粗糙时，滑楔体与水平面间夹角为

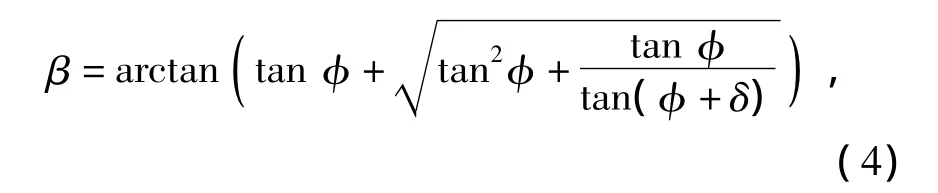
式中:φ为土体内摩擦角;δ为墙-土摩擦角.

1.2 环向应力系数

墙后土体产生较大位移时，其位移是向心的，因土体的移动出现环向挤压效应，从而增加土体的自身稳定性.V.G.Berezantzev［2］假定环向应力 σθ与第一主应力 σ1相等对环效应进行了考虑，E.G.Prater［3］、Cheng Y.M.等［4］、Liu F.Q. 等［5］通过引入环向应力系数λ研究其对土压力的影响，认为主动土压力随着环向应力系数的增大而减小.本研究中假定环向应力系数等于λ.

1.3 主动侧压力系数

墙后土体产生向心移动的过程中，在自重荷载的作用下，将相对于墙体向下移动，引起墙土间摩擦力的发生作用，作用在墙体上的竖直和水平力不再是主应力，墙背处的主应力将发生偏转，并假定偏转后的大主应力与水平面的夹角为θ，在墙及滑移面间形成竖向土拱，竖向土拱为小主应力拱，假设拱形为圆弧形.筒形墙体半径为r，在任意深度z处滑移面半径为R，在该深度处取dz厚度、角度为dα的微分单元进行分析.图1为莫尔应力圆.

图1 莫尔应力圆

由图1可知，墙后某一点的水平向和竖直向应力可以表述为

由图 1 可知，σhtan δ=(σh- σ3)tan θ，当 δ≠0时，可得主应力偏转角为

并对夹角为dα断面进行侧压力系数分析，在深度z处，小主应力示意图如图2所示.

图2 小主应力示意图

在该深度处滑移面半径为

式中R1为小主应力拱线半径.并可以得到z处的滑移面与墙体间的表面面积:

任一点A处的水平侧压力为

整理可得

由σh+σv=σ1+σ3可得

因此，作用在微分单元上的平均竖向应力为

式中dSz为黑色阴影部分面积.可以得到:

通过式(5)，(14)可得到新的主动侧压力系数:

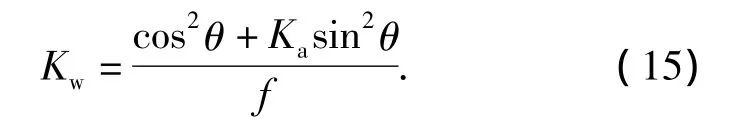
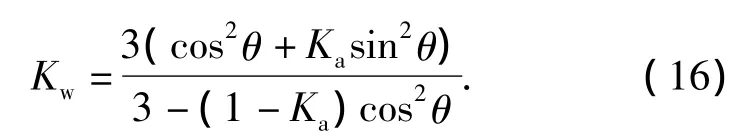
当墙体半径无限大，且为光滑竖直时，即δ=0，大主应力不发生偏转，即θ=90°，Kw减小为朗肯主动土压力系数.即

1.4 筒形墙体主动土压力

假定墙后土体为均质的无黏性土，内摩擦角为φ，筒形挡土墙竖直，墙体粗糙，墙-土摩擦角为δ，墙顶填土水平，墙体总高为H.作用在微分单元上的力如图3所示.

图3 微分单元受力分析

图3中，σz为作用在微分单元顶面的平均竖向应力，σz+dσz为作用于微分单元底面的平均竖向应力，σr为作用于筒形墙体上的径向应力，τ1为筒形墙体与土体的竖直剪应力，σθ为环向应力，σn为作用于滑移面的法向应力，τ2为作用于滑移面上的剪应力.

由微分单元的径向受力平衡可得

整理可得

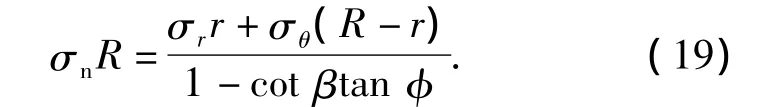
由微分单元竖直方向的受力平衡可得

整理可得

方程(21)即为求解筒形挡土墙主动土压力的基本方程.则由σr=Kwσz可以得到作用于墙体上的主动土压力.

2 结果分析

2.1 理论结果比较

将得到的考虑空间拱效应的筒形挡土墙主动土压力结果与公式(1)、E.G.Prater［3］、Cheng Y.M.等［4］、V.G.Berezantzev［2］及朗肯静止、主动土压力结果进行比较(见图4).计算参数如下:φ=30°，K0=1-sin φ =0.5，Kα=tan2(45°- φ/2)=0.33，r=2 m，γ =18 kN·m-3，H=30 m.

图4 主动土压力结果比较

由图 4 可知，公式(1)、E.G.Prater［3］、Cheng Y.M.等［4］、V.G.Berezantzev［2］及本研究所得结果较朗肯主动土压力小，其土压力沿深度均为非线性分布.K.Terzaghi和 V.G.Berezantzev［2］的结果变化相似，土压力随深度先线性增加，后趋于定值.而E.G.Prater［3］得到结果则显示土压力达到某一深度后趋于0，即在达到该深度后随着深度增加可不加支护，显然不符合实际.在z≤12 m时，本研究(λ=1.0)结果较 K.Terzaghi及 V.G.Berezantzev［2］大;12 m ＜z≤20 m时，本研究结果介于K.Terzaghi及V.G.Berezantzev［2］结果之间，随深度增加趋于破裂面底部时，其值减小.

2.2 环向应力系数对土压力的影响

由式(21)得到了不同环向应力系数λ时的土压力分布.计算参数为 φ =30°，γ =18 kN·m-3，δ=20°，H=30 m，r=2 m，下文中未作说明的均采用该参数.图5为Ka≤λ≤1的土压力分布图.由图5可知，环向应力系数λ对土压力有较大影响，随着λ的增大，土压力逐渐减小.开挖中，随土体位移增大，作用于筒形墙体后的土体将产生向心移动而压缩，环向应力系数λ将增大，土体自身稳定性增强，作用在墙体上的主动土压力则减小.

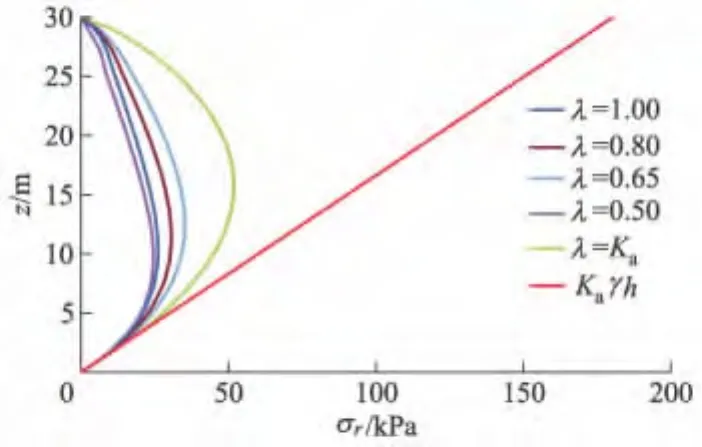
图5 λ对主动土压力的影响

2.3 墙-土摩擦角对土压力的影响

图6为墙-土摩擦角δ=5°～30°时主动土压力与墙体深度的关系.土压力随着δ的增大而增大，但δ＜25°时，其对土压力的影响较小.而随着δ增大到土体内摩擦角时，土压力增大明显，且在z≤4 m，土压力较朗肯主动土压力大，而随着深度的增加，土压力随之减小，土压力小于朗肯主动土压力.

图6 墙-土摩擦角对主动土压力的影响

2.4 半径对土压力的影响

图7为不同半径r时的土压力与深度的关系.由图7可知，主动土压力随着r的增大而增大，墙体上部土压力更接近于朗肯主动土压力值.这是由于r的增大，筒形挡土墙将趋于平面挡土墙，其环向拱效应减弱，导致作用于墙体上的土压力增大.

图7 半径对主动土压力的影响

2.5 与试验结果比较

S.Imamura等［12］离心试验中的土体自重为15.2 kN·m-3，土体内摩擦角为42°，筒形墙体直径为120 mm，高度为500 mm，在离心加速度100 g的条件下试验.图8为主动土压力理论值与试验值的比较.由图8可知，S.Imamura等［12］试验的土压力沿深度非线性分布，且其值明显较朗肯主动土压力小，随着深度增加而增大，与郎肯主动土压力差值也增大.可见，本研究与 S.Imamura等［12］试验结果吻合较好.

图8 主动土压力理论值与试验值的比较

3 结论

1)筒形挡土墙后土体在向心移动时，同时受到竖向土拱和环向拱效应的共同作用，本研究考虑竖向土拱和环向拱效应，得到了筒形挡土墙主动土压力解析式.

2)考虑拱效应的筒形挡土墙主动土压力受环向应力系数、墙-土内摩擦角及半径的影响，随环向应力系数的减小、墙-土摩擦角的增大及半径的增大，土压力逐渐增大.

3)对本研究与S.Imamura等［12］离心试验进行了比较，两者结果基本吻合.

References)

［1］Shin Y W，Sagong M.Ground pressure acting on cylindrical retaining wall of a shaft in soft ground［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26:3689-3696.

［2］Berzantzev V G.Earth pressure on the cylindrical retaining walls［C］∥Proceedings of International Society of Soil Mechanics and Foundation Engineering Conference on Earth Pressure Problems.London:Butterworths，1958:21-27.

［3］Prater E G.An examination of some theories of earth pressure on shaft linings［J］.Canadian Geotechnical Journal，1977，14:91-106.

［4］Cheng Y M，Hu Y Y，Wei W B.General axisymmetric active earth pressure by method of characteristics-theory and numerical formulation［J］.International Journal of Geomechanics，2007，7(1):1-15.

［5］Liu F Q，Wang J H，Zhang L L.Axi-symmetric active earth pressure obtained by the slip line method with a general tangential stress coefficient［J］.Computers and Geotechnics，2009，36:352-358.

［6］Ueno K，Yokoyama Y，Ohi A，et al.Earth pressures acting on flexible circular shafts in sand［C］∥Proceedings of Geotechnical Aspects of Underground Construction in Soft Ground.Tokyo， Japan:Balkema， Rotterdam，1996:237-242.

［7］Fujii T，Hagiwara T，Kusakabe O.Active failure mechanism of a deep circular shaft in dry sand［C］∥Proceedings of Geotechnical Aspects of Underground Construction in Soft Ground.Balkema:Rotterdam，1996:137-142.

［8］Paik K H，Salgado R.Estimation of active earth pressure against rigid retaining walls considering arching effects［J］.Geotechnique，2003，53(7):643-653.

［9］彭述权，周 健，樊 玲，等.考虑土拱效应刚性挡墙土压力研究［J］.岩土力学，2008，29(10):2701-2707.

Peng Shuquan，Zhou Jian，Fan Ling，et al.Research on earth pressure of rigid retaining wall considering soil arching［J］.Rock and Soil Mechanics，2008，29(10):2701-2707.(in Chinese)

［10］马英明.立井厚表土层地压的理论与实践［J］.中国矿业学院学报，1979(1):45-68.

Ma Yingming.Theory and practice of ground pressure on shaft due to thick overburden［J］.Journal of China University of Mining＆Technology，1979(1):45-68.(in Chinese)

［11］Wong R C K，Kaiswe P K.Behaviour of vertical shafts reevaluation of model test results and evaluation of field measurements［J］.Canadian Geotechnical Journal，1988，25:338-352.

［12］Imamura S，Nomoto T，FuJii T，et al.Earth pressure acting on a deep shaft and the movements of adjacent ground in sand［C］∥Proceedings of the International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground.Tokyo，Japan:Balkema，Rotterdam，1999:647-652.